Построение сечений многогранников

1. Построение сечений многогранников

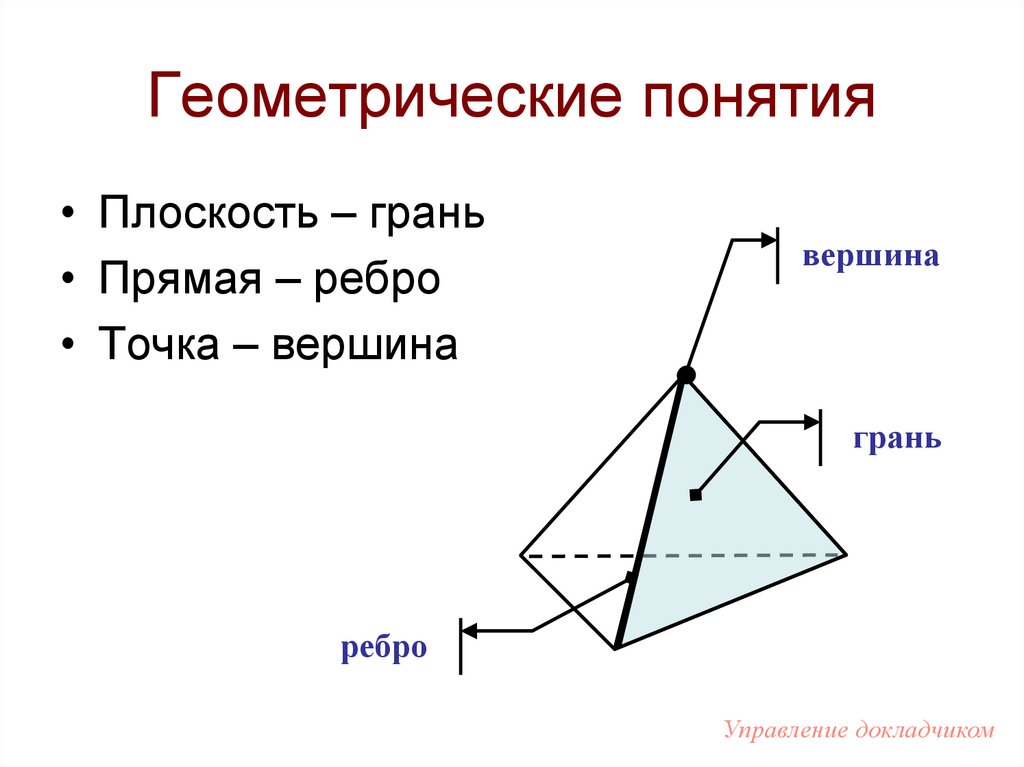
2. Геометрические понятия

• Плоскость – грань
• Прямая – ребро
• Точка – вершина
вершина
грань
ребро
Управление докладчиком

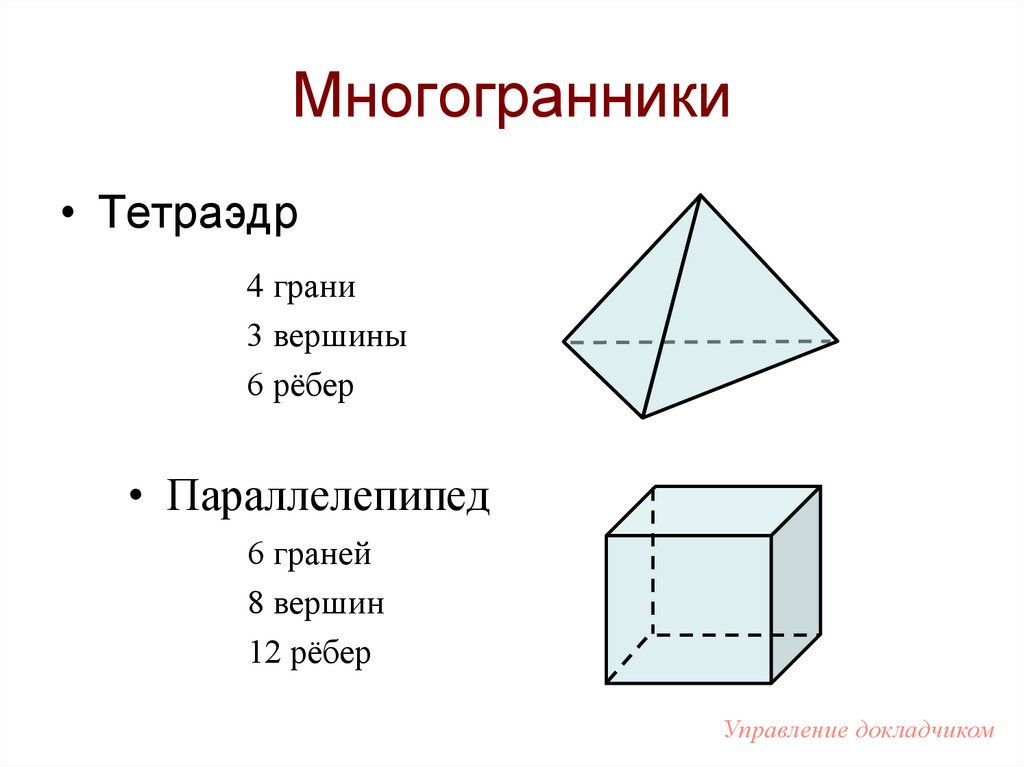
3. Многогранники

• Тетраэдр
4 грани
3 вершины
6 рёбер
• Параллелепипед
6 граней
8 вершин
12 рёбер
Управление докладчиком

4.

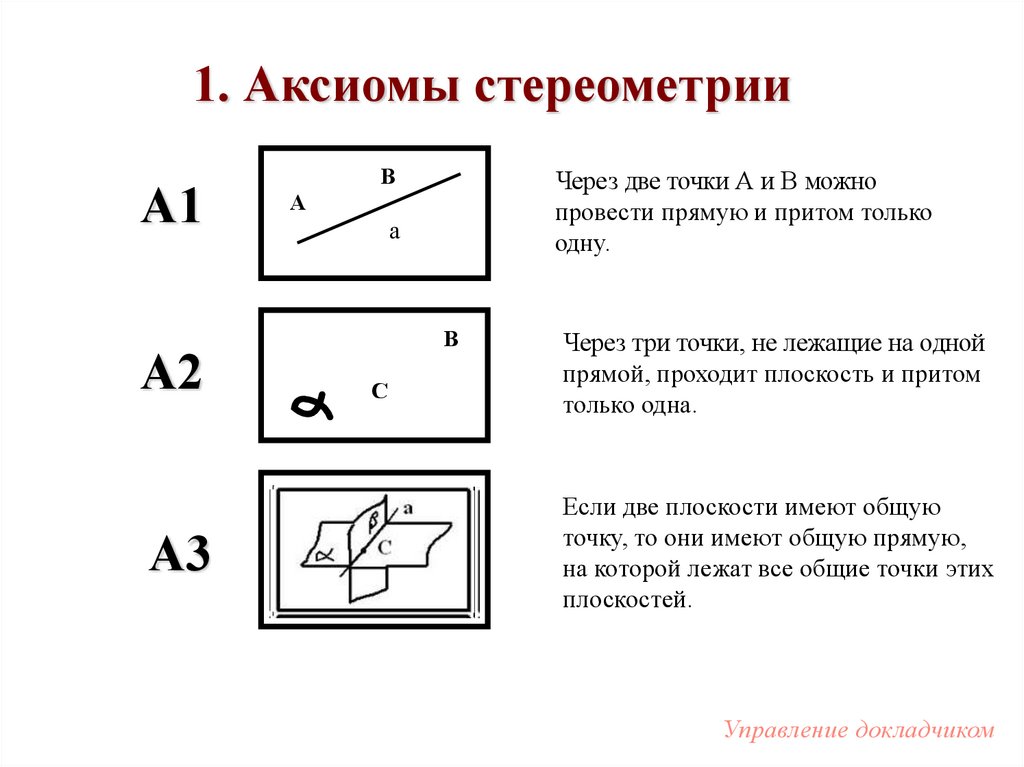
1. Аксиомы стереометрии
А1
В
А
а
А
А2
А3
Через две точки А и В можно
провести прямую и притом только
одну.
В
С
Через три точки, не лежащие на одной
прямой, проходит плоскость и притом
только одна.
Если две плоскости имеют общую
точку, то они имеют общую прямую,
на которой лежат все общие точки этих
плоскостей.
Управление докладчиком

5.

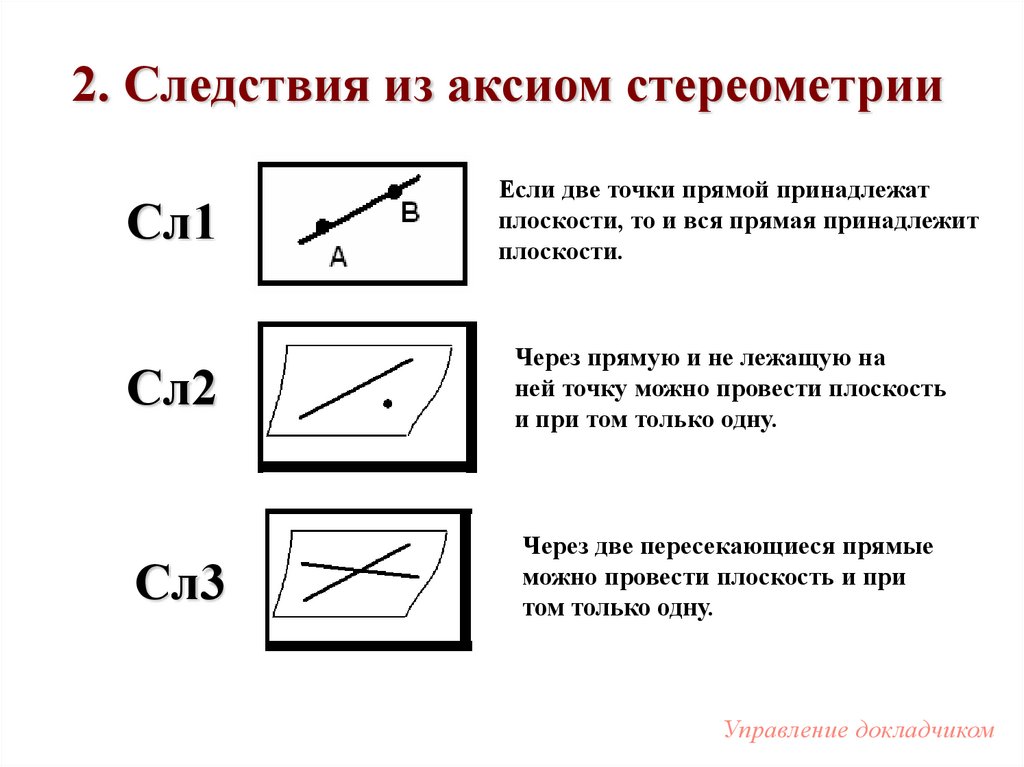
2. Следствия из аксиом стереометрии
Сл1
Сл2
Сл3
Если две точки прямой принадлежат
плоскости, то и вся прямая принадлежит
плоскости.
Через прямую и не лежащую на
ней точку можно провести плоскость
и при том только одну.
Через две пересекающиеся прямые
можно провести плоскость и при
том только одну.
Управление докладчиком

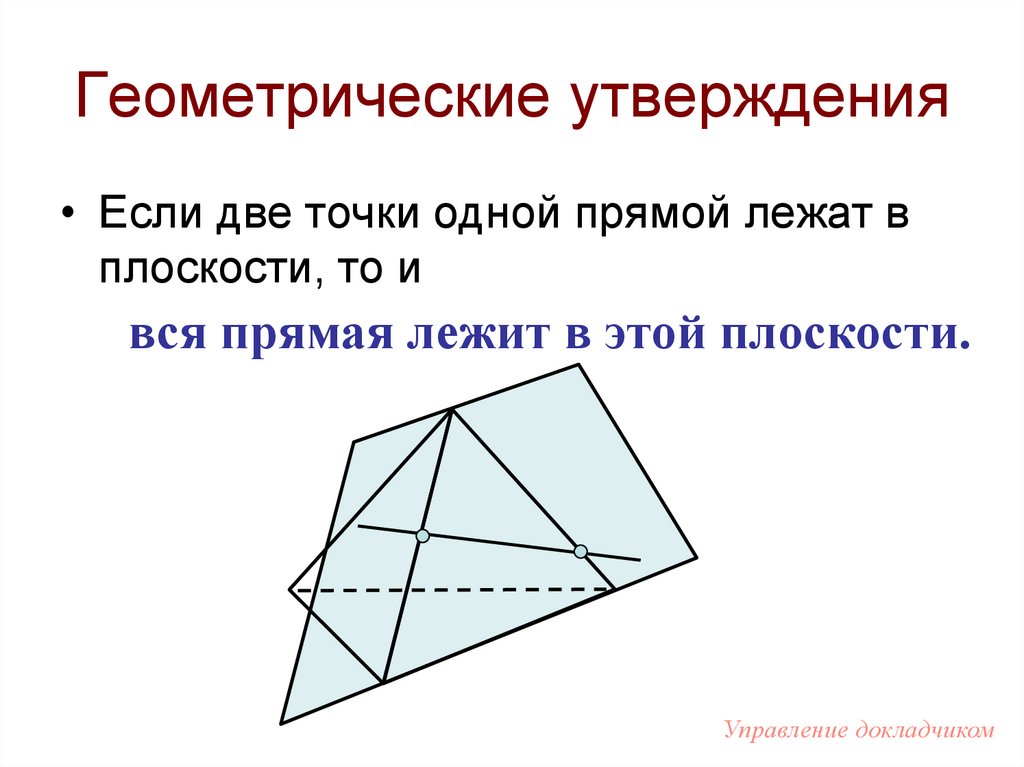
6. Геометрические утверждения

• Если две точки одной прямой лежат в
плоскости, то и
вся прямая лежит в этой плоскости.
Управление докладчиком

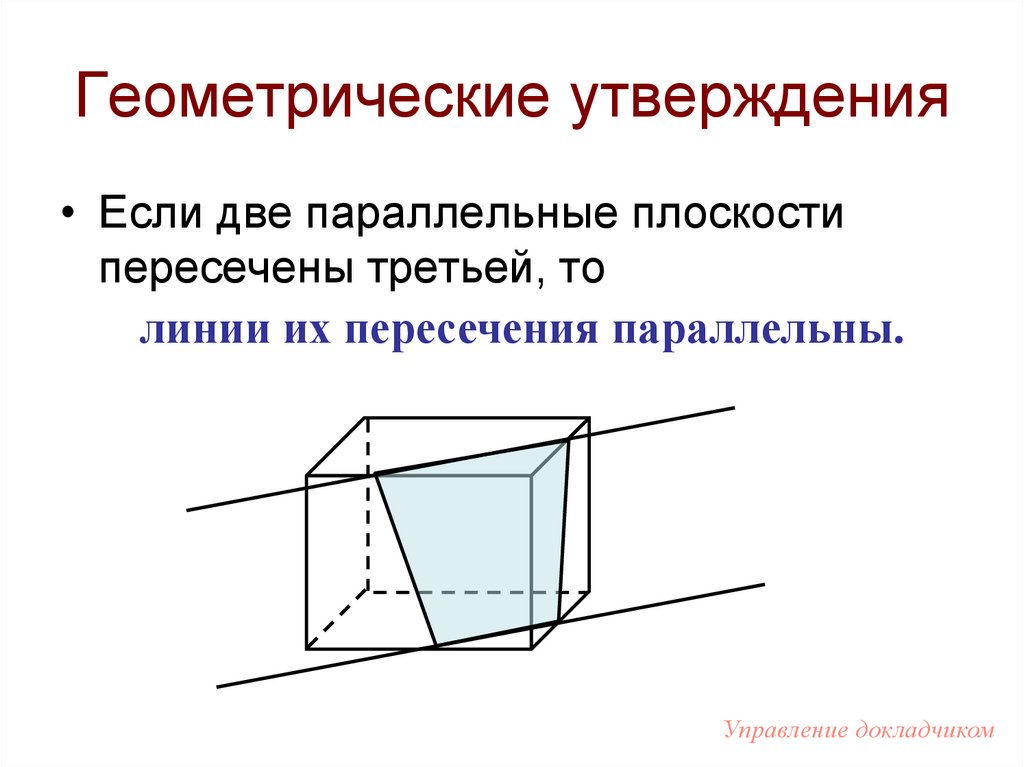
7. Геометрические утверждения

• Если две параллельные плоскости
пересечены третьей, то
линии их пересечения параллельны.
Управление докладчиком

8. Пересечение двух пересекающихся прямых

найти легко: точка, в
которой они пересекаются
на чертеже,и есть
изображение их точки
пересечения в
пространстве.
Управление докладчиком

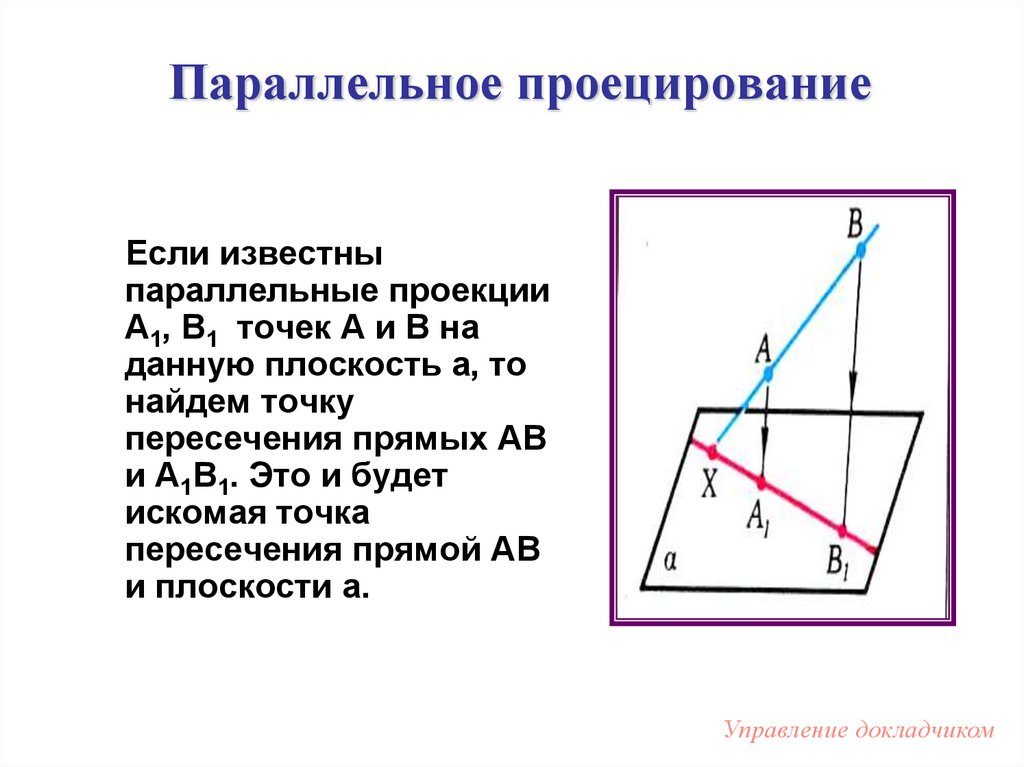
9. Параллельное проецирование

Если известны
параллельные проекции
А1, В1 точек А и В на
данную плоскость а, то
найдем точку
пересечения прямых АВ
и А1В1. Это и будет
искомая точка
пересечения прямой АВ
и плоскости а.
Управление докладчиком

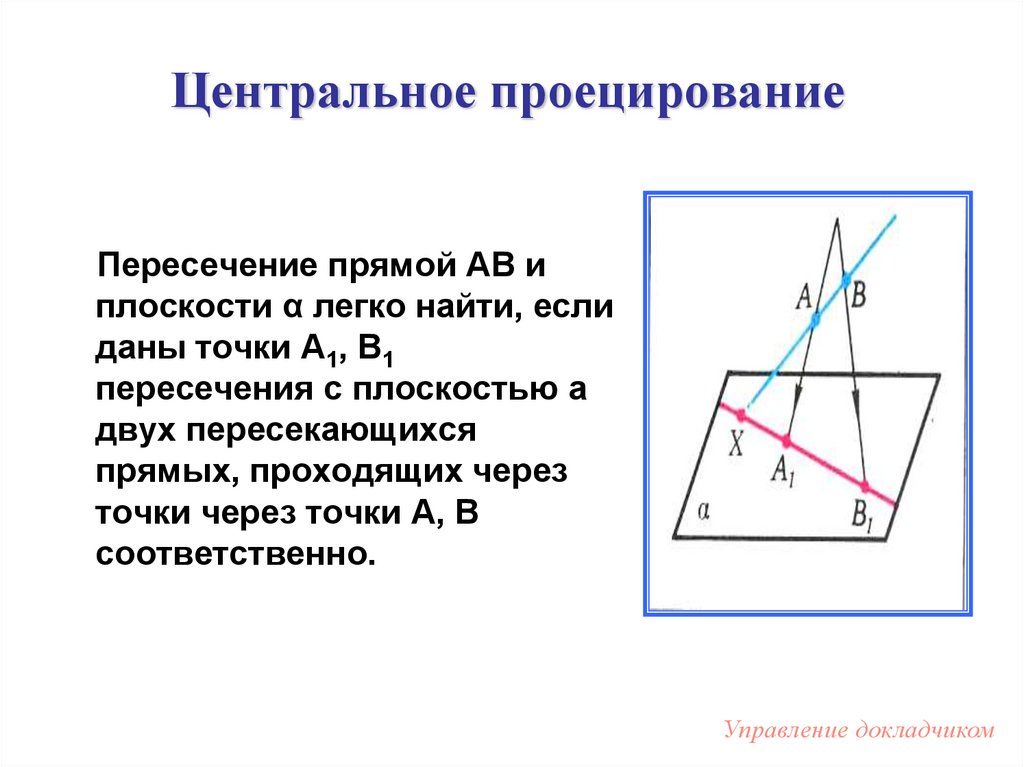
10. Центральное проецирование

Пересечение прямой АВ и
плоскости α легко найти, если
даны точки А1, В1
пересечения с плоскостью а
двух пересекающихся
прямых, проходящих через
точки через точки А, В
соответственно.
Управление докладчиком

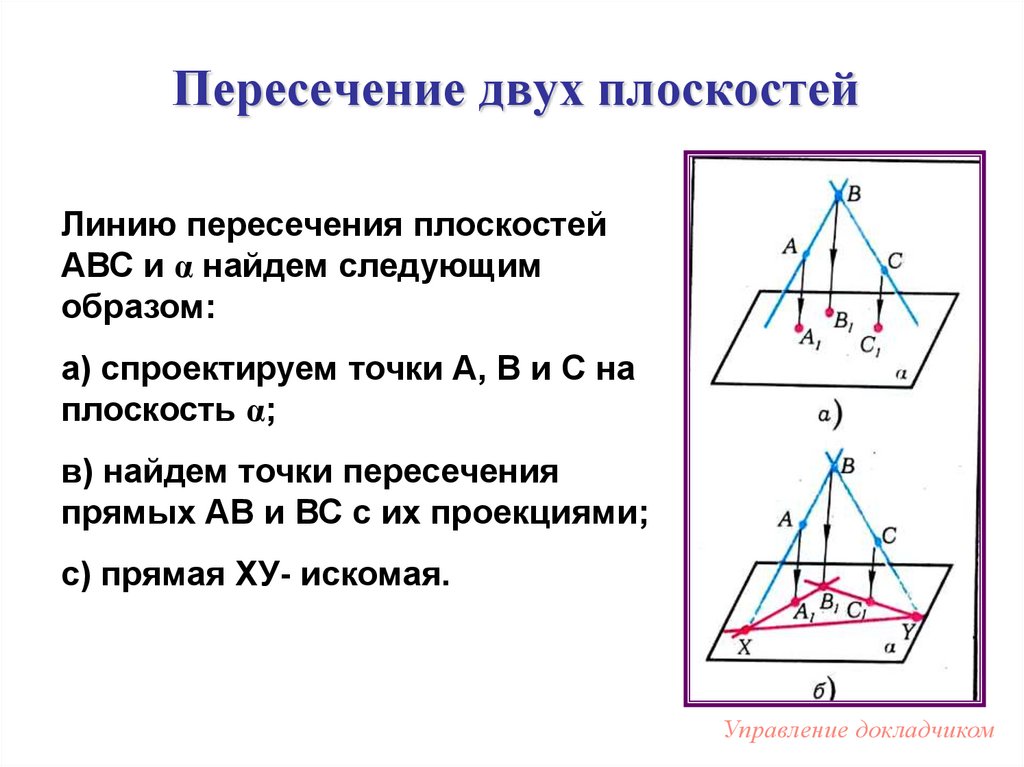
11. Пересечение двух плоскостей

Линию пересечения плоскостей
АВС и α найдем следующим
образом:
а) спроектируем точки А, В и С на
плоскость α;
в) найдем точки пересечения
прямых АВ и ВС с их проекциями;
с) прямая ХУ- искомая.
Управление докладчиком

12.

Опорные задачи:
Задача на нахождение двух точек
искомой прямой
Задача на построение точки пересечения
прямой и плоскости
Задача на построение линии
пересечения двух плоскостей
Управление докладчиком

13.

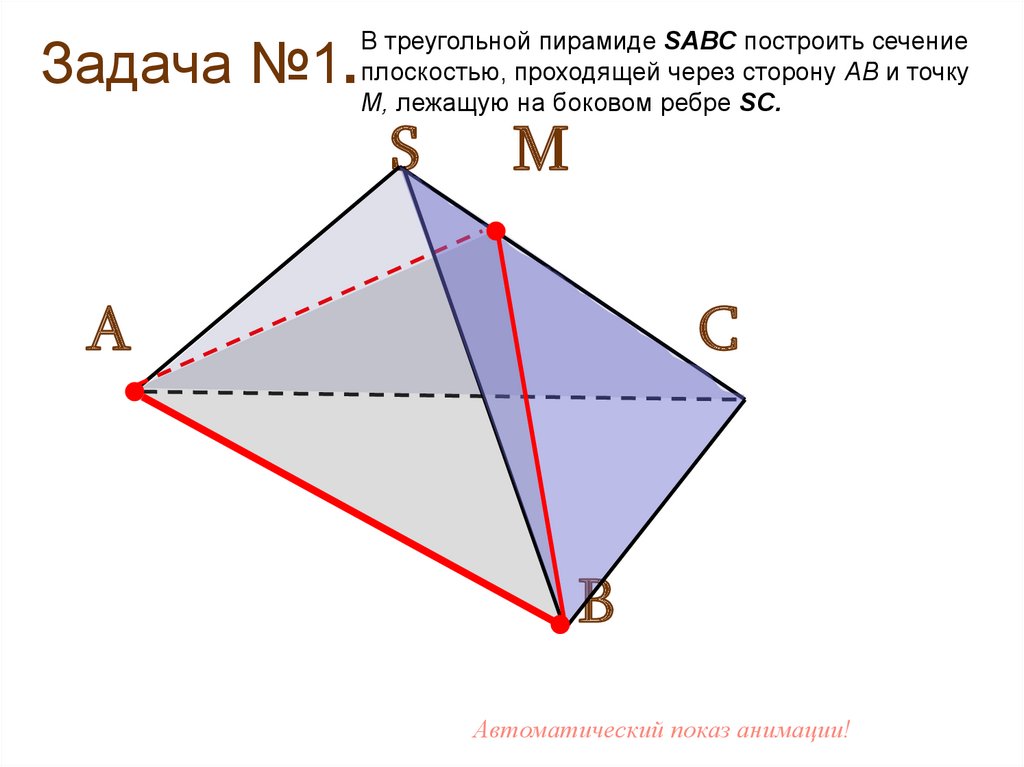
Задача №1.
В треугольной пирамиде SABC построить сечение
плоскостью, проходящей через сторону АВ и точку
М, лежащую на боковом ребре SC.
S
М
А
С
В
Автоматический показ анимации!

14.

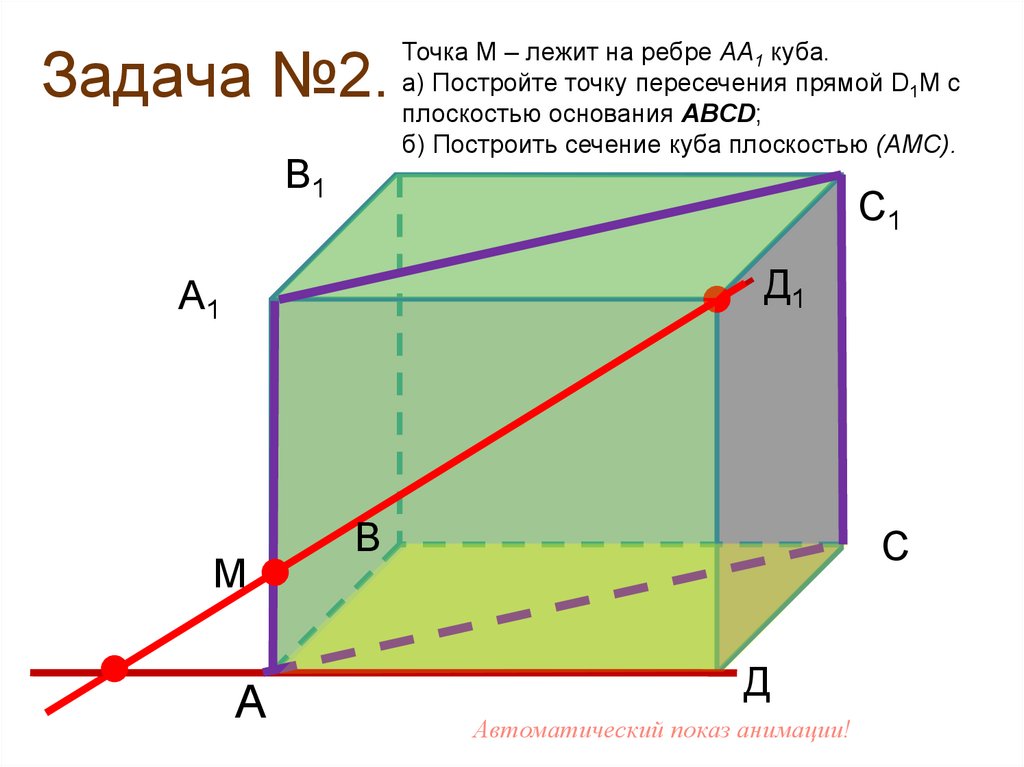
Задача №2.
В1
Точка М – лежит на ребре АА1 куба.
a) Постройте точку пересечения прямой D1M с
плоскостью основания ABCD;
б) Построить сечение куба плоскостью (АМС).
С1
Д1
А1
М
А
В
С
Д
Автоматический показ анимации!

15.

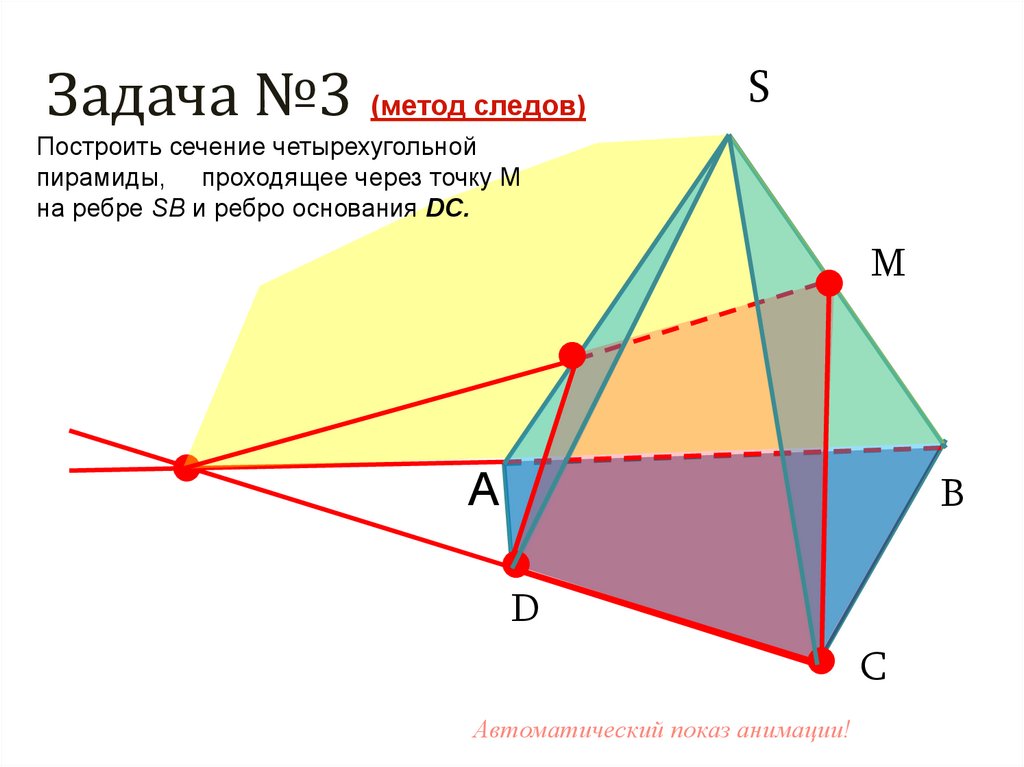
Задача №3 (метод следов)
S
Построить сечение четырехугольной
пирамиды, проходящее через точку М
на ребре SB и ребро основания DC.
М
А
В
D
С
Автоматический показ анимации!

16.

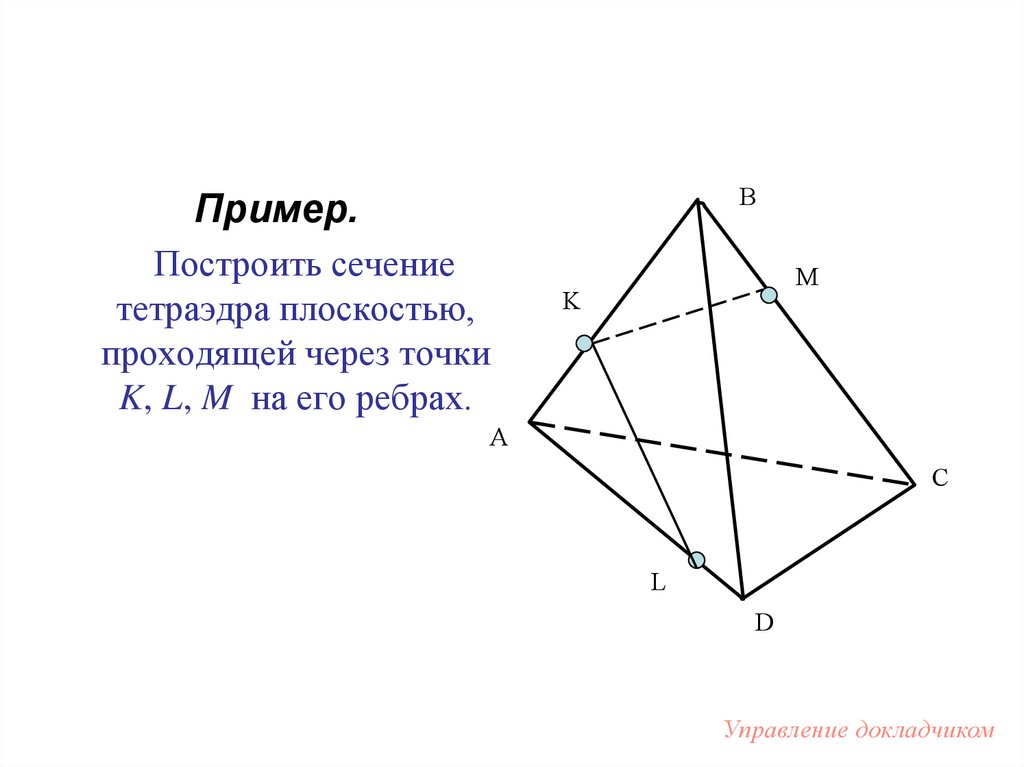
B
Пример.
Построить сечение
тетраэдра плоскостью,
проходящей через точки
K, L, M на его ребрах.
M
K
A
C
L
D
Управление докладчиком

17.

B
Пример.
Построить сечение
тетраэдра плоскостью,
проходящей через точки
K, L, M на его ребрах.
M
K
A
C
L
D
Управление докладчиком

18.

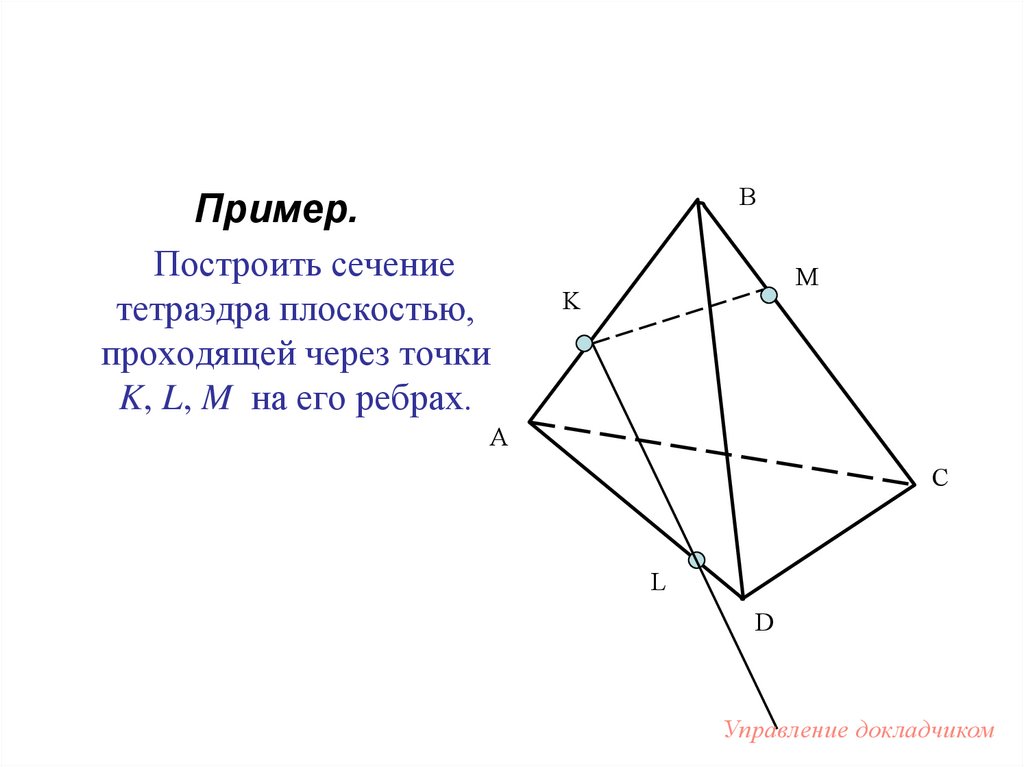
B
Пример.
Построить сечение
тетраэдра плоскостью,
проходящей через точки
K, L, M на его ребрах.
M
K
A
C
L
D
Управление докладчиком

19.

B
Пример.
Построить сечение
тетраэдра плоскостью,
проходящей через точки
K, L, M на его ребрах.
M
K
A
C
L
D
Управление докладчиком

20.

B
Пример.
Построить сечение
тетраэдра плоскостью,
проходящей через точки
K, L, M на его ребрах.
M
K
A
C
L
F
D
Управление докладчиком

21.

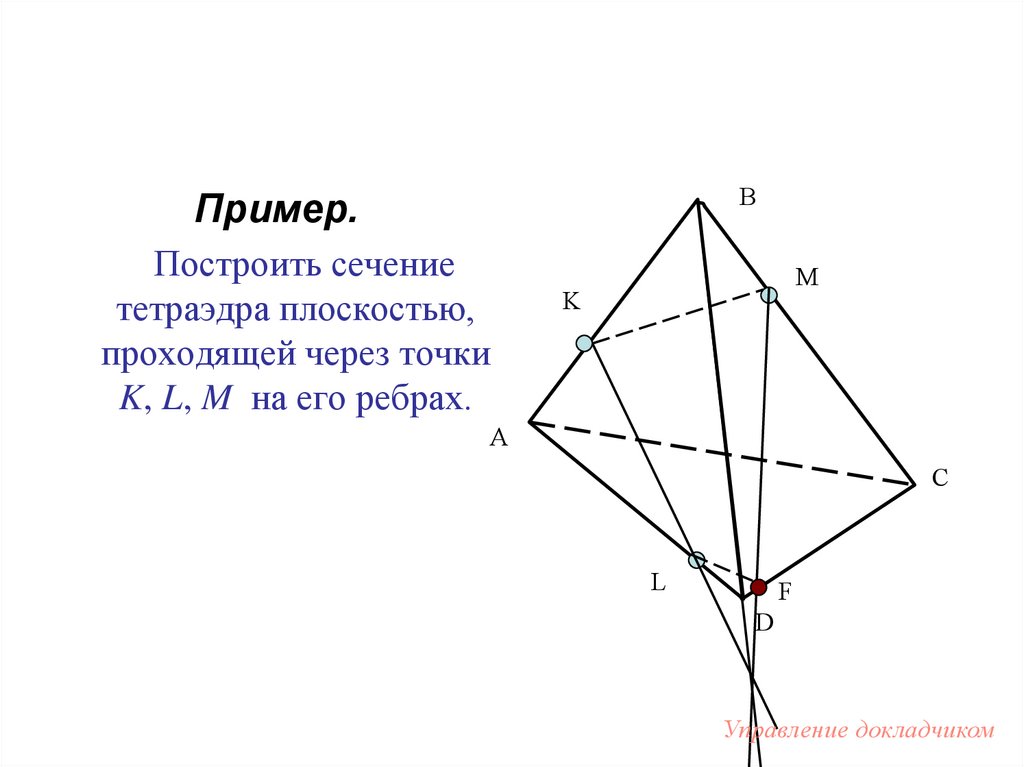
B
Пример.
Построить сечение
тетраэдра плоскостью,
проходящей через точки
K, L, M на его ребрах.
M
K
A
C
L
F
D
Управление докладчиком

22.

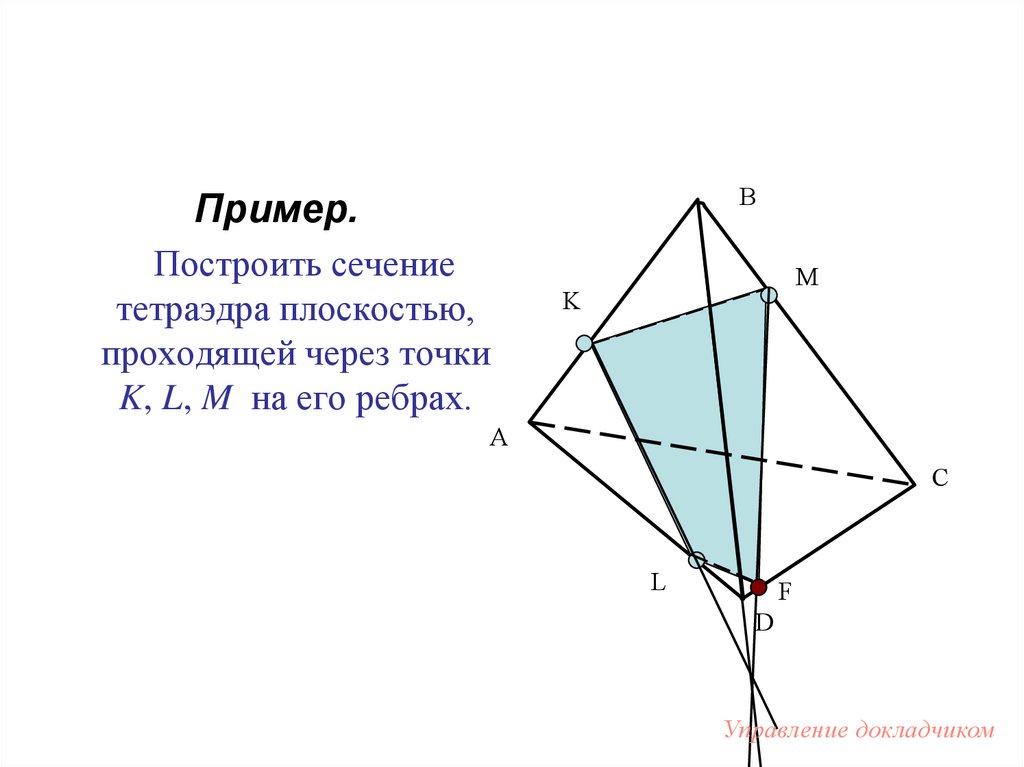
B
Пример.
Построить сечение
тетраэдра плоскостью,
проходящей через точки
K, L, M на его ребрах.
M
K
A
C
L
F
D
Управление докладчиком

23.

Пример.
S
Дана пирамида SABCD.
B
A
C
D
Автоматический показ анимации!

24.

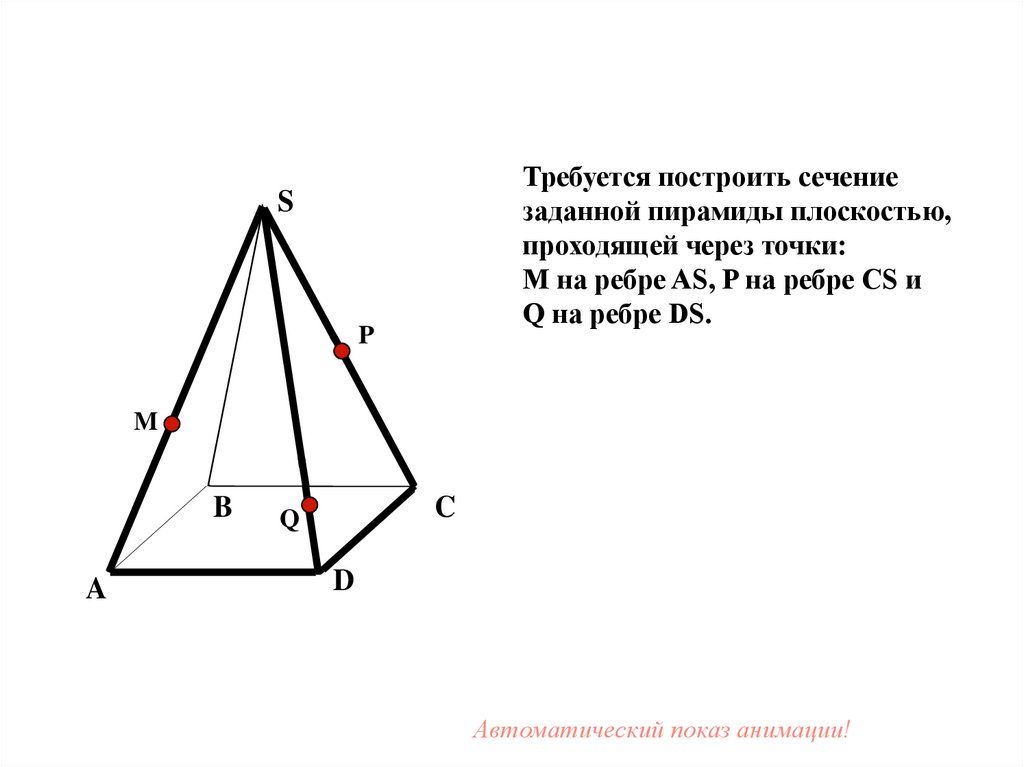
Требуется построить сечение
заданной пирамиды плоскостью,
проходящей через точки:
М на ребре AS, P на ребре CS и
Q на ребре DS.
S
P
M
B
A
C
Q
D
Автоматический показ анимации!

25.

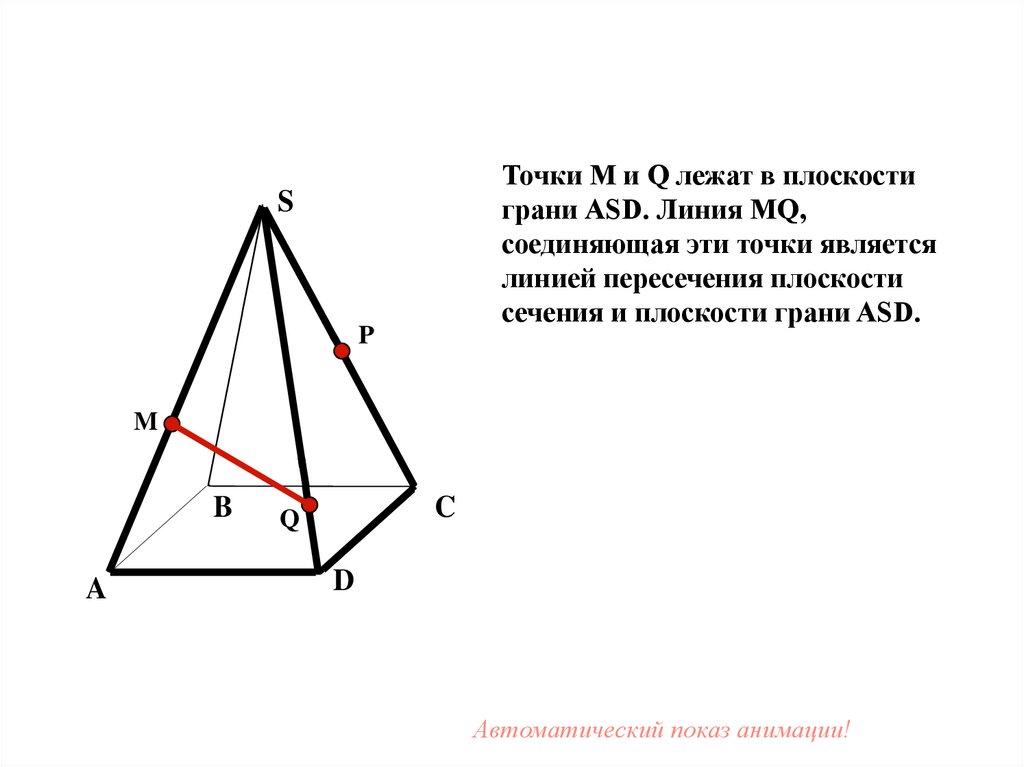
Точки M и Q лежат в плоскости
грани АSD. Линия МQ,
соединяющая эти точки является
линией пересечения плоскости
сечения и плоскости грани ASD.
S
P
M
B
A
C
Q
D
Автоматический показ анимации!

26.

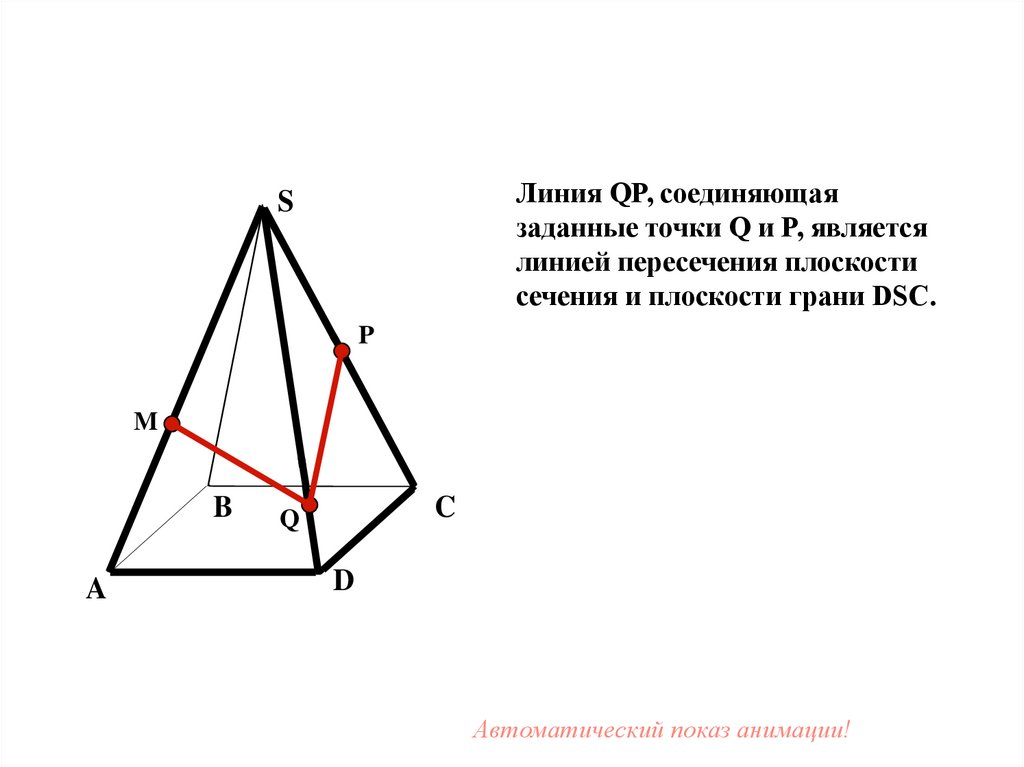
Линия QP, соединяющая
заданные точки Q и P, является
линией пересечения плоскости
сечения и плоскости грани DSC.
S
P
M
B
A
C
Q
D
Автоматический показ анимации!

27.

Линии MQ и AD лежат в одной
плоскости грани ASD. Найдём
точку Е, как точку пересечения
линий MQ и AD.
Точка Е будет принадлежать
искомой плоскости сечения, так
как она принадлежит линии MQ,
лежащей в этой плоскости.
S
P
M
B
A
C
Q
D
Е
Автоматический показ анимации!

28.

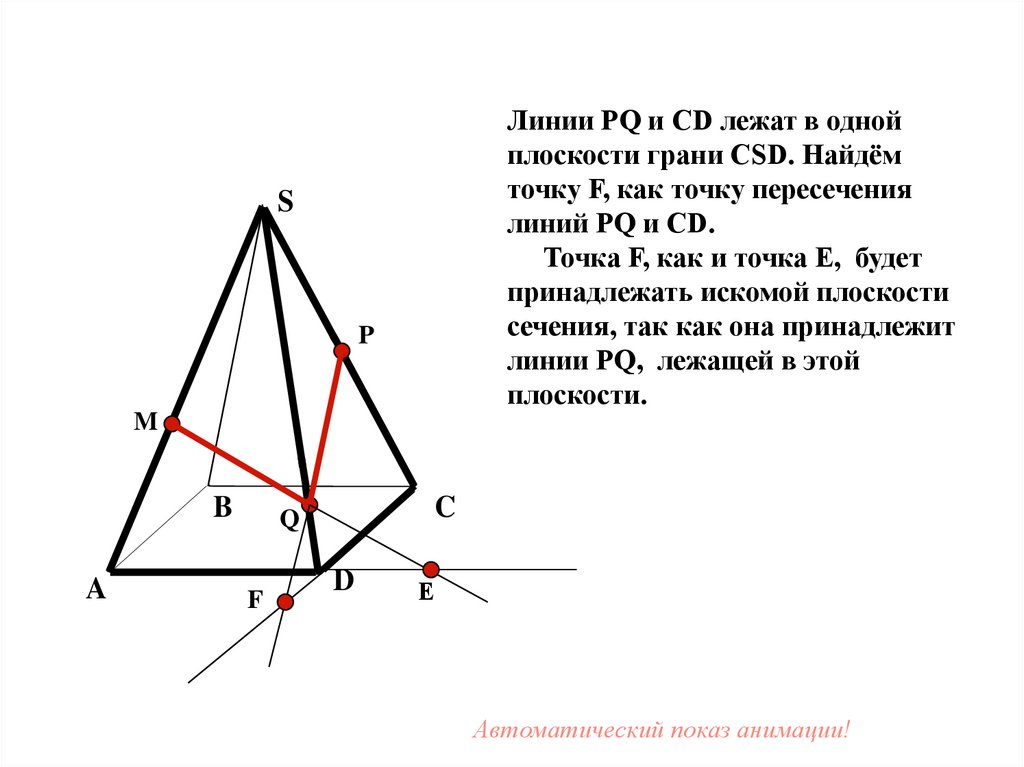
Линии PQ и CD лежат в одной
плоскости грани CSD. Найдём
точку F, как точку пересечения
линий PQ и CD.
Точка F, как и точка Е, будет
принадлежать искомой плоскости
сечения, так как она принадлежит
линии PQ, лежащей в этой
плоскости.
S
P
M
B
A
C
Q
F
D
Е
Автоматический показ анимации!

29.

Точки Е и F принадлежат
плоскости сечения и плоскости
основания пирамиды, поэтому
линия EF будет линией
пересечения плоскости сечения и
плоскости основания пирамиды.
S
P
M
B
A
C
Q
F
D
Е
Автоматический показ анимации!

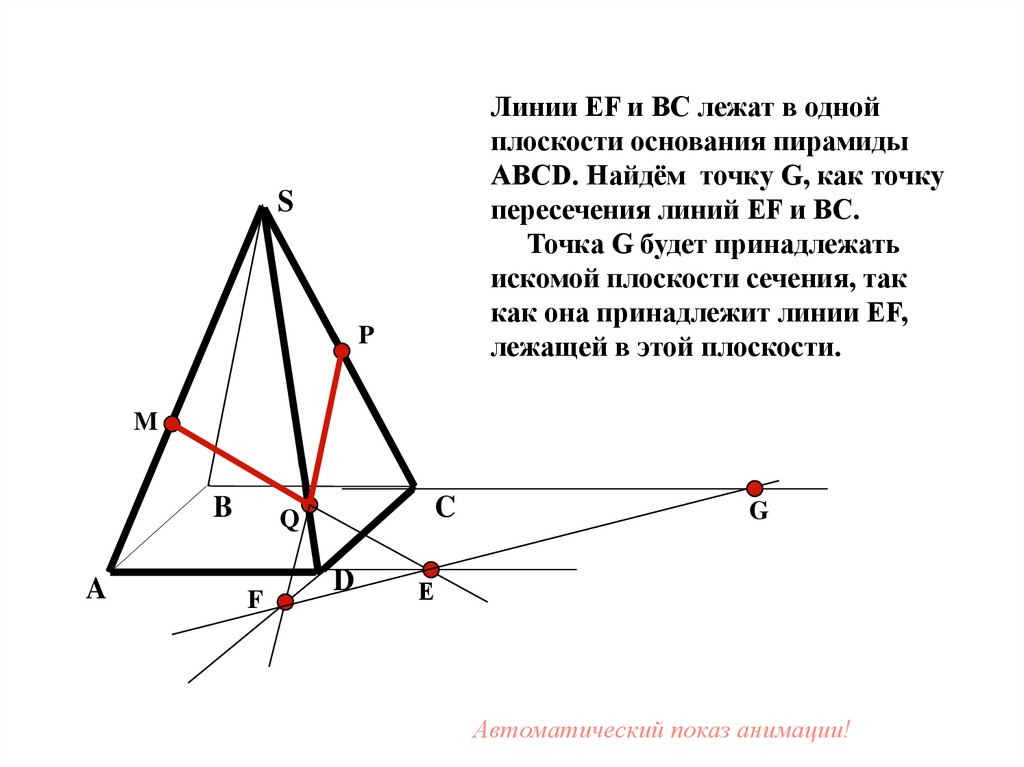
30.

Линии EF и BC лежат в одной
плоскости основания пирамиды
ABCD. Найдём точку G, как точку
пересечения линий EF и BC.
Точка G будет принадлежать
искомой плоскости сечения, так
как она принадлежит линии EF,
лежащей в этой плоскости.
S
P
M
B
A
C
Q
F
D
G
Е
Автоматический показ анимации!

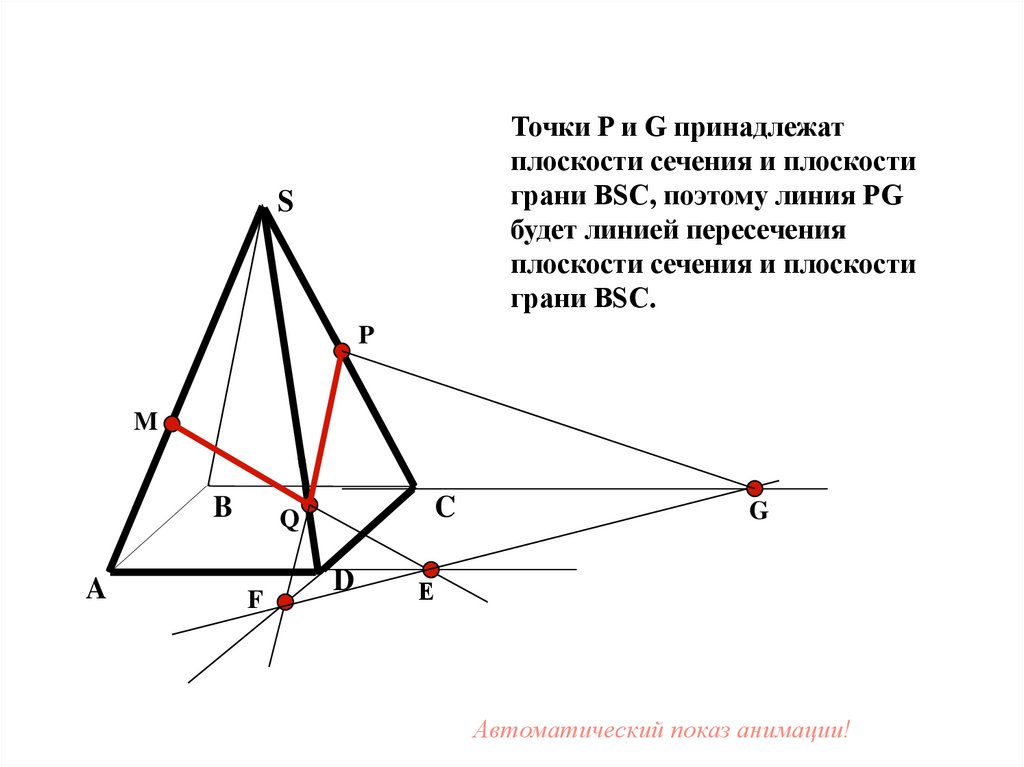
31.

Точки P и G принадлежат
плоскости сечения и плоскости
грани BSC, поэтому линия PG
будет линией пересечения
плоскости сечения и плоскости
грани BSC.
S
P
M
B
A
C
Q
F
D
G
Е
Автоматический показ анимации!

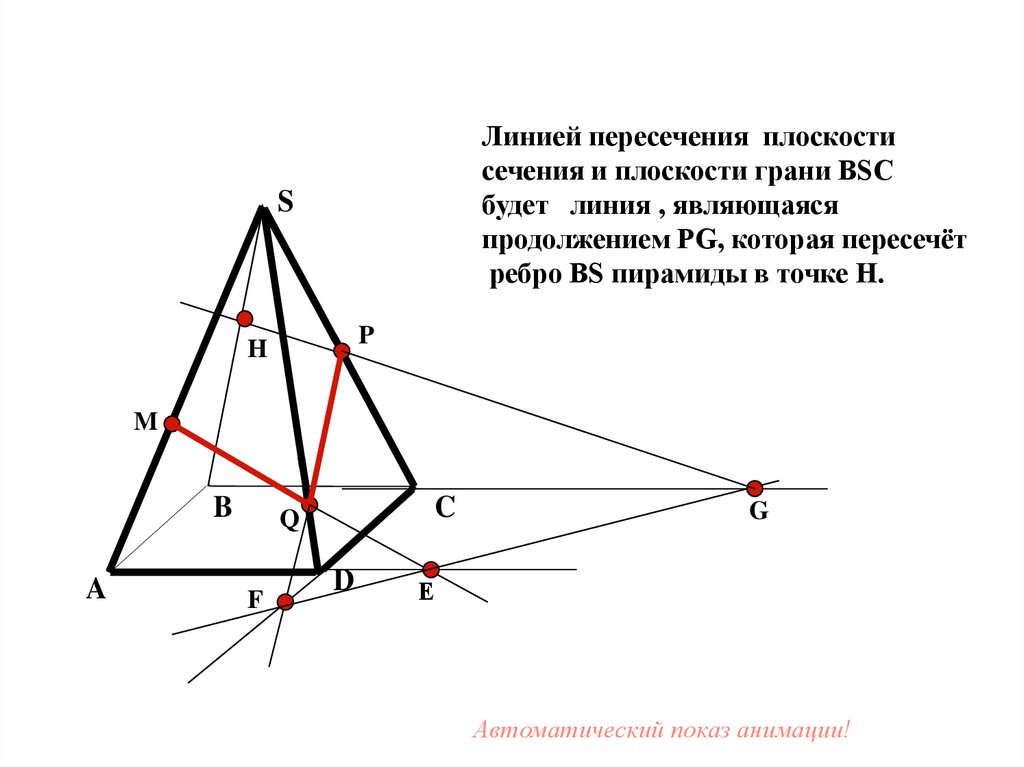
32.

Линией пересечения плоскости
сечения и плоскости грани BSC
будет линия , являющаяся
продолжением PG, которая пересечёт
ребро BS пирамиды в точке H.
S
P
H
M
B
A
C
Q
F
D
G
Е
Автоматический показ анимации!

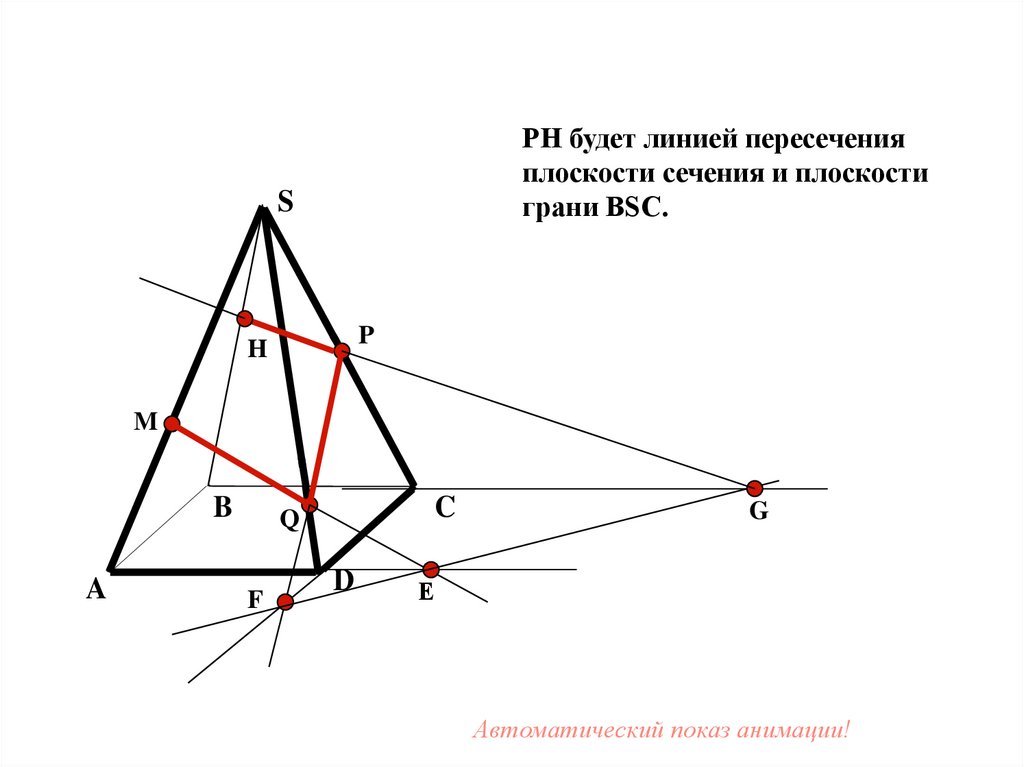
33.

PH будет линией пересечения
плоскости сечения и плоскости
грани BSC.
S
P
H
M
B
A
C
Q
F
D
G
Е
Автоматический показ анимации!

34.

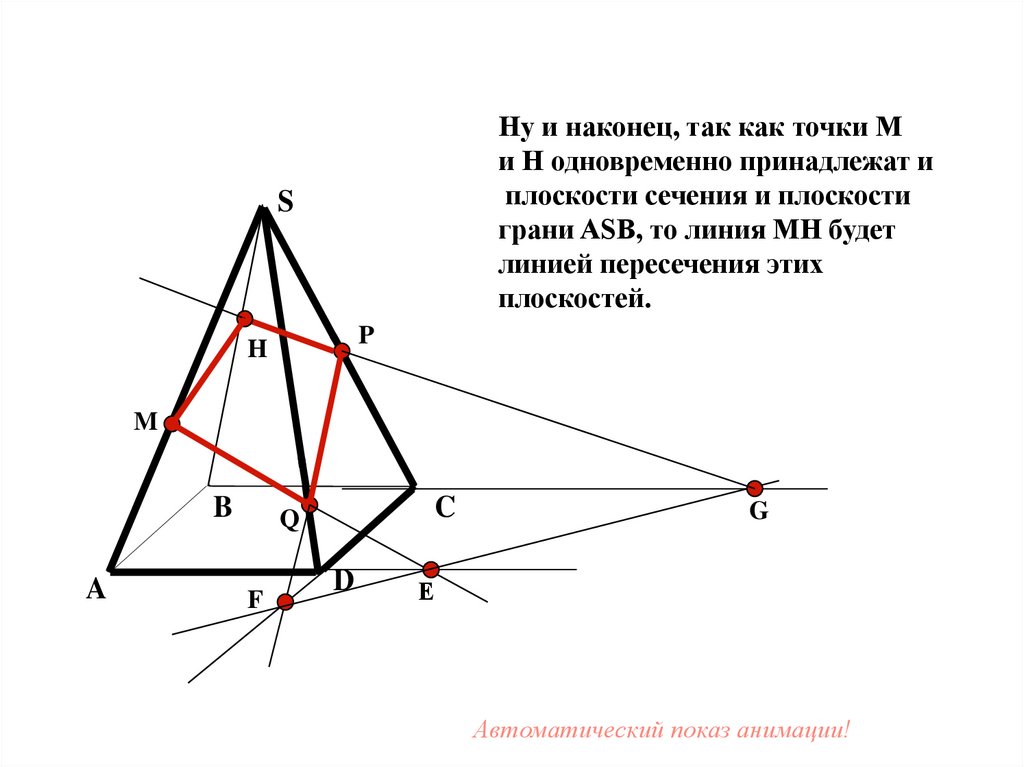
Ну и наконец, так как точки M
и H одновременно принадлежат и
плоскости сечения и плоскости
грани ASB, то линия MH будет
линией пересечения этих
плоскостей.
S
P
H
M
B
A
C
Q
F
D
G
Е
Автоматический показ анимации!

35.

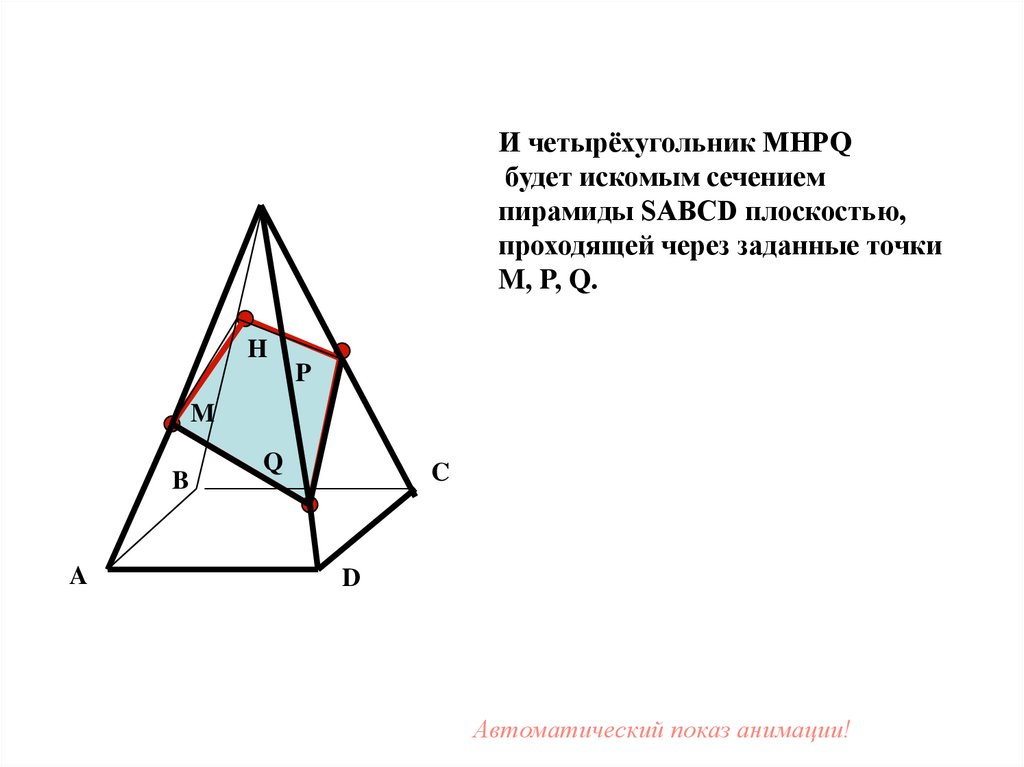
И четырёхугольник MHPQ
будет искомым сечением
пирамиды SABCD плоскостью,
проходящей через заданные точки
M, P, Q.
H
P
M
B
A
Q
C
D
Автоматический показ анимации!

36.

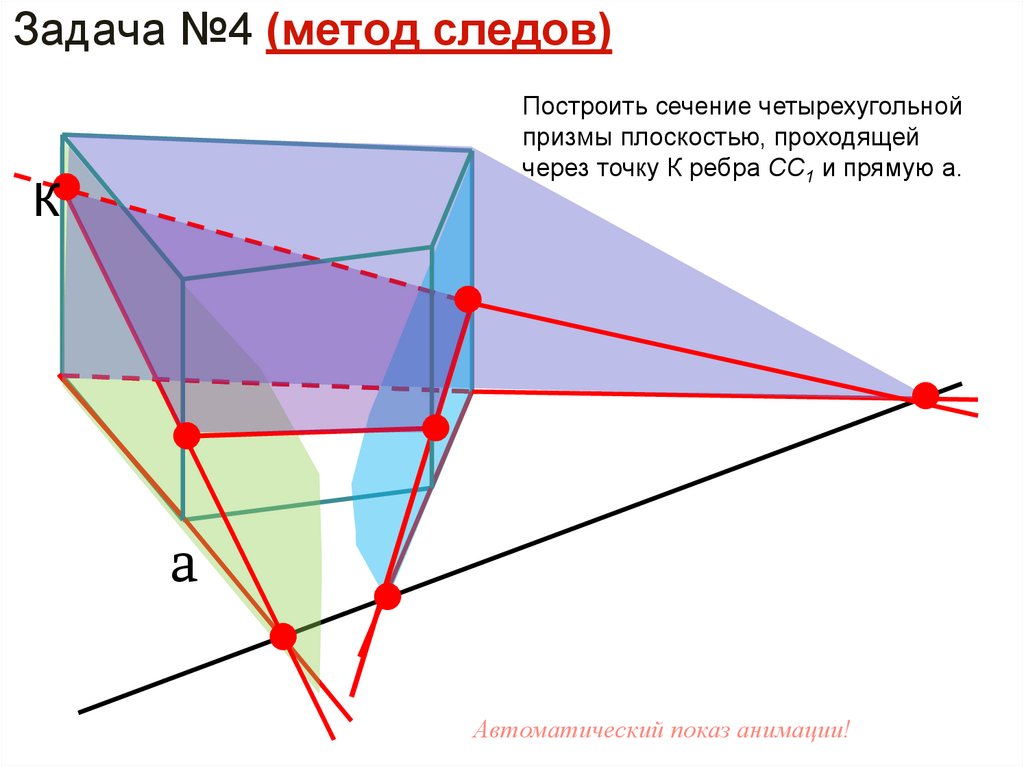
Задача №4 (метод следов)
Построить сечение четырехугольной
призмы плоскостью, проходящей
через точку К ребра CС1 и прямую a.
К
a
Автоматический показ анимации!

37.

Пример.
B
A
C
E
A1
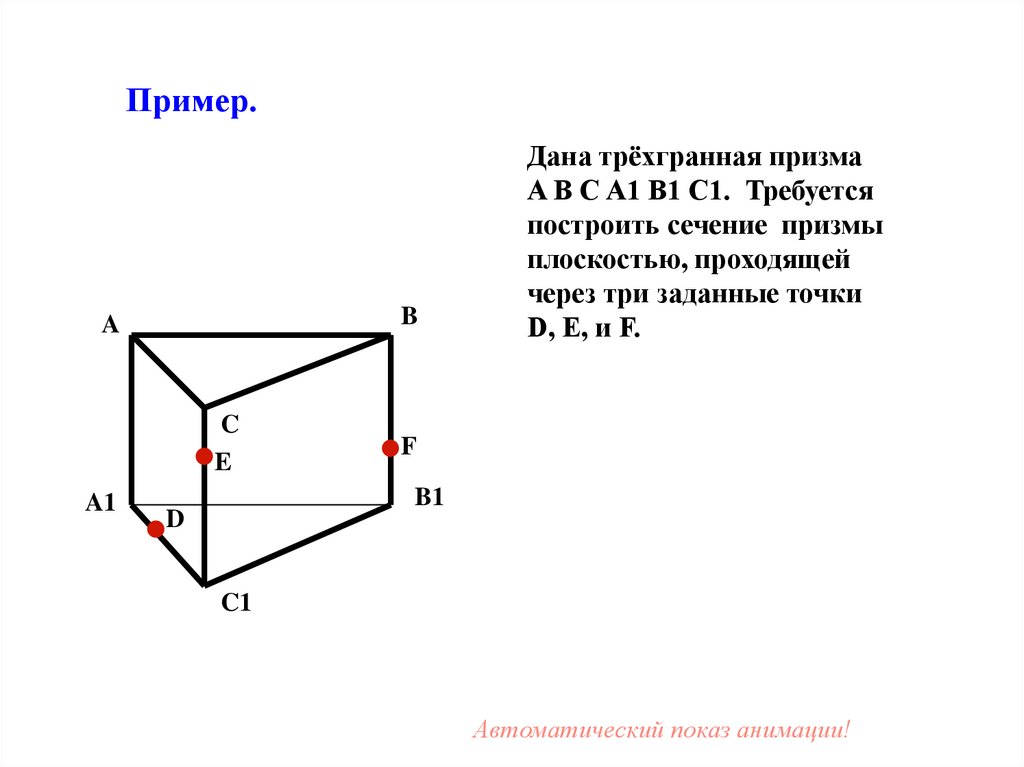
Дана трёхгранная призма
A B C A1 B1 C1. Требуется
построить сечение призмы
плоскостью, проходящей
через три заданные точки
D, E, и F.
F
B1
D
C1
Автоматический показ анимации!

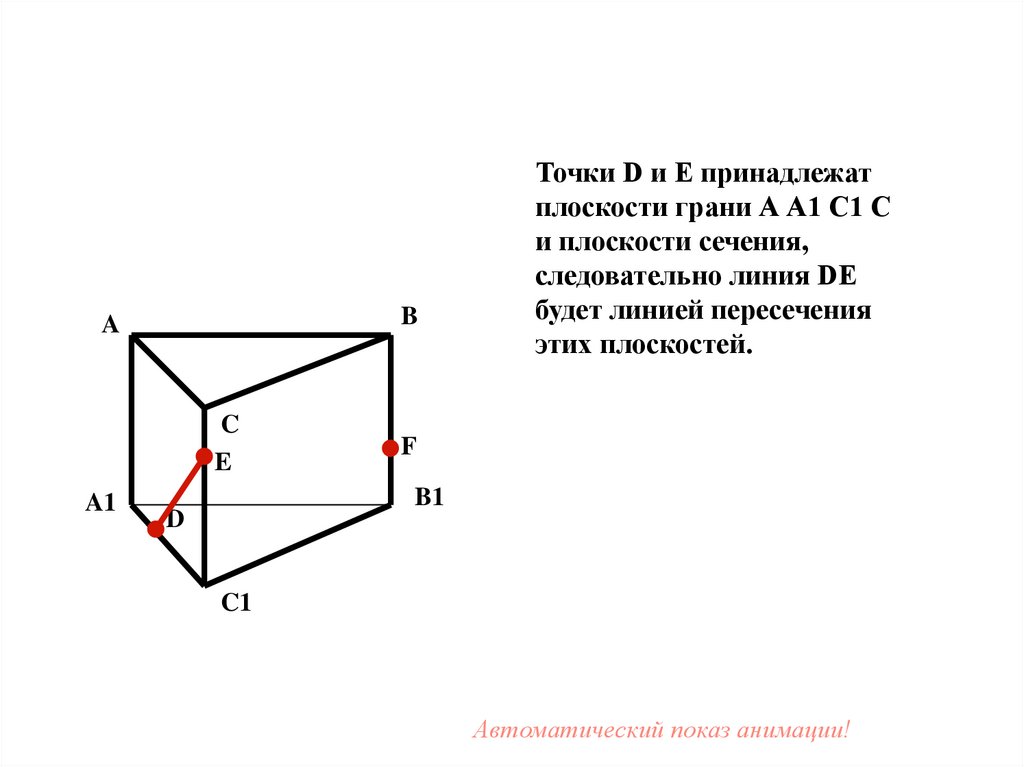
38.

B
A
C
E
A1
Точки D и E принадлежат
плоскости грани А А1 С1 С
и плоскости сечения,
следовательно линия DE
будет линией пересечения
этих плоскостей.
F
B1
D
C1
Автоматический показ анимации!

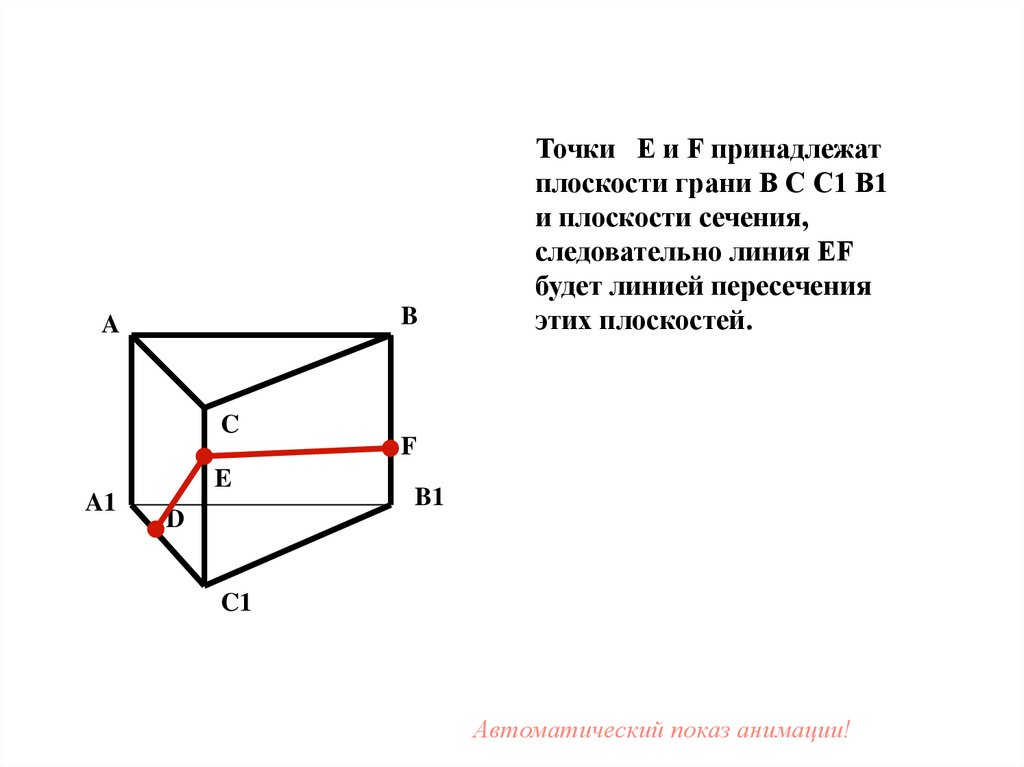
39.

B
A
C
E
A1
D
Точки E и F принадлежат
плоскости грани B C C1 B1
и плоскости сечения,
следовательно линия EF
будет линией пересечения
этих плоскостей.
F
B1
C1
Автоматический показ анимации!

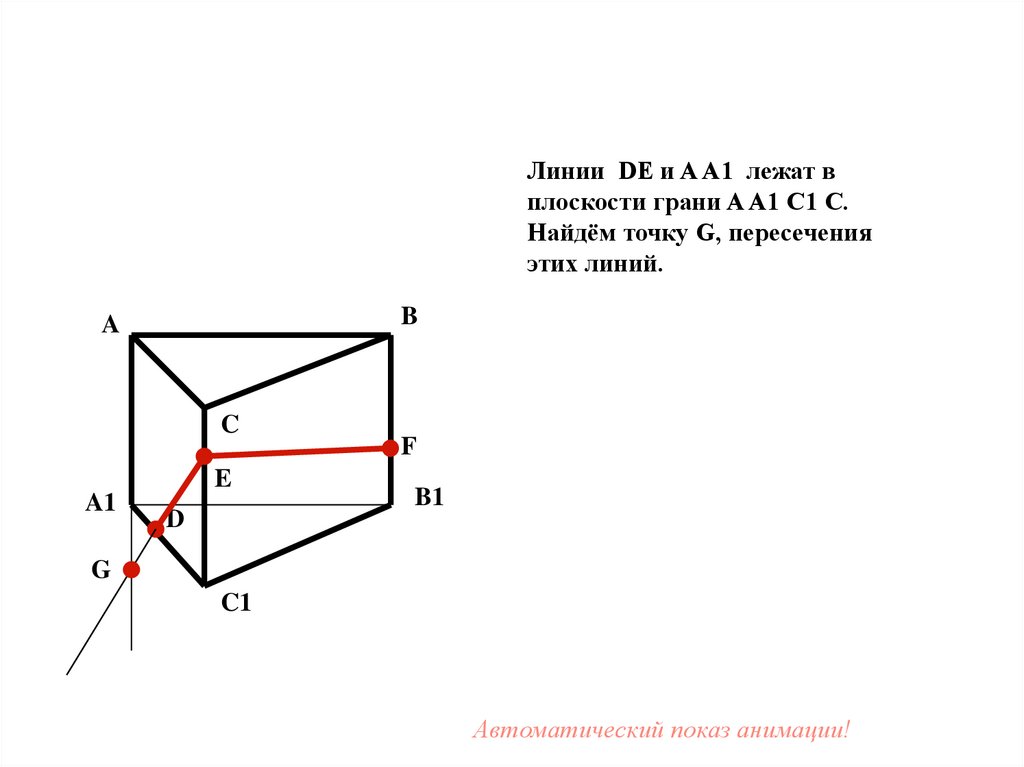
40.

Линии DE и A A1 лежат в
плоскости грани A A1 C1 C.
Найдём точку G, пересечения
этих линий.
B
A
C
E
A1
D
F
B1
G
C1
Автоматический показ анимации!

41.

B
A
C
E
A1
D
Точка G принадлежит плоскости
сечения, так как она принадлежит
линии DE. Точки G и F принадлежат
плоскости грани A A1 B1 B и
плоскости сечения, следовательно
линия GF будет линией пересечения
этих плоскостей.
F
B1
G
C1
Автоматический показ анимации!

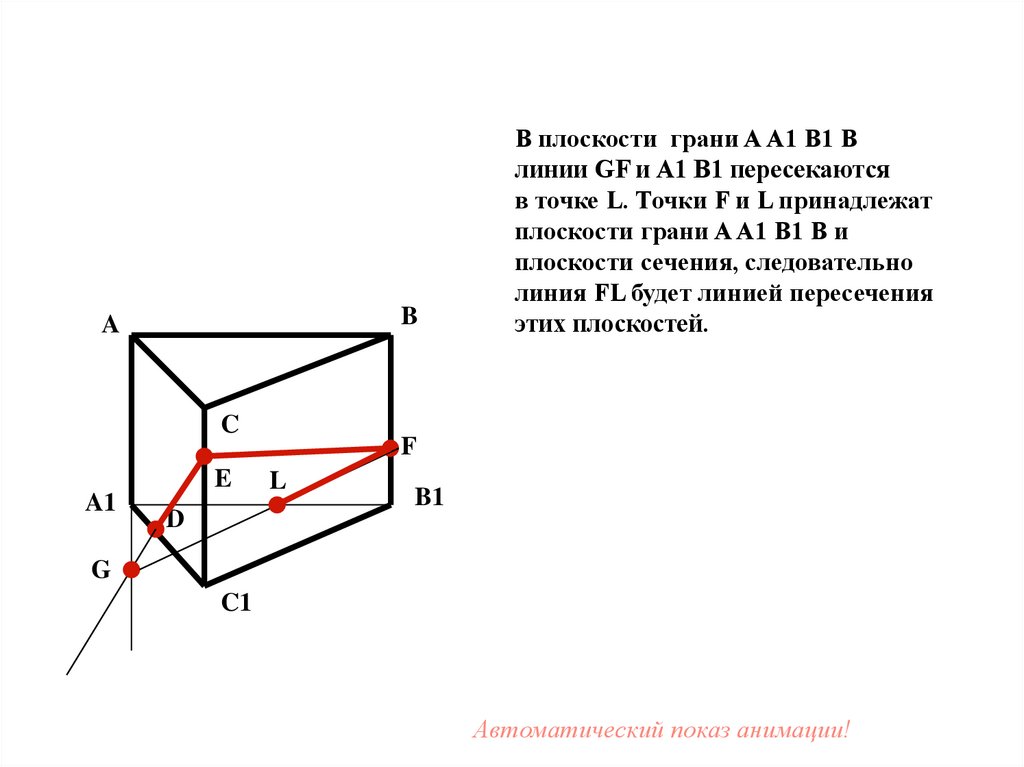
42.

B
A
C
E
A1
D
В плоскости грани A A1 B1 B
линии GF и A1 B1 пересекаются
в точке L. Точки F и L принадлежат
плоскости грани A A1 B1 B и
плоскости сечения, следовательно
линия FL будет линией пересечения
этих плоскостей.
F
L
B1
G
C1
Автоматический показ анимации!

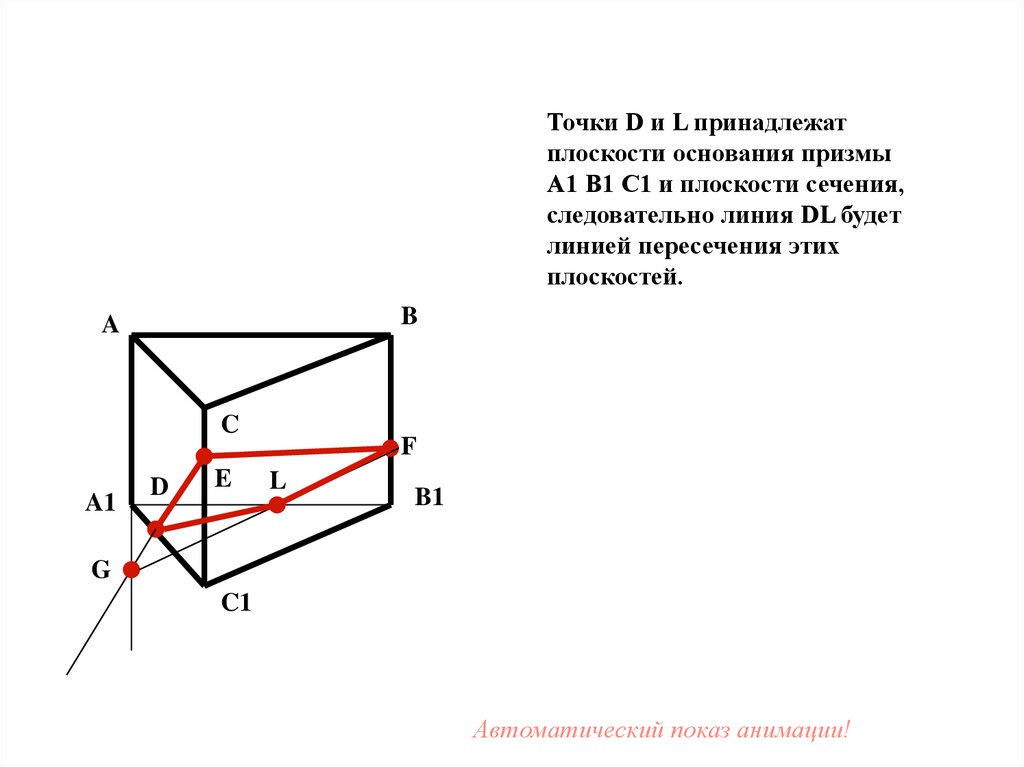
43.

Точки D и L принадлежат
плоскости основания призмы
A1 B1 C1 и плоскости сечения,
следовательно линия DL будет
линией пересечения этих
плоскостей.
B
A
C
A1
D
E
F
L
B1
G
C1
Автоматический показ анимации!

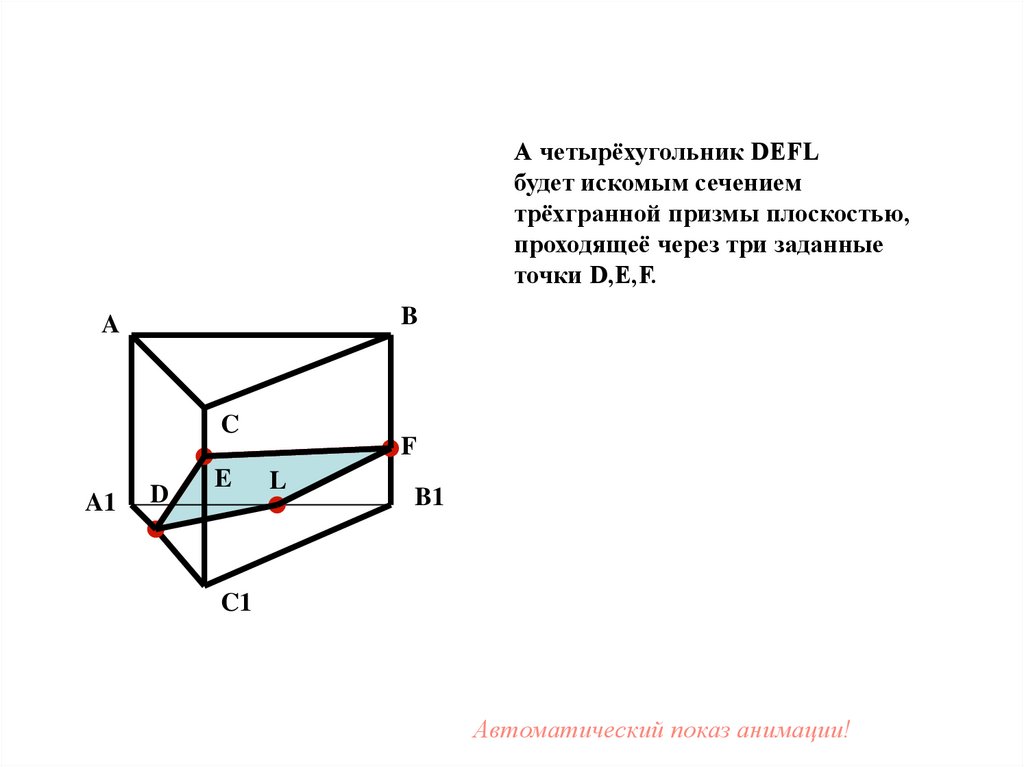
44.

А четырёхугольник DEFL
будет искомым сечением
трёхгранной призмы плоскостью,
проходящеё через три заданные
точки D,E,F.
B
A
C
A1
D
E
F
L
B1
C1
Автоматический показ анимации!

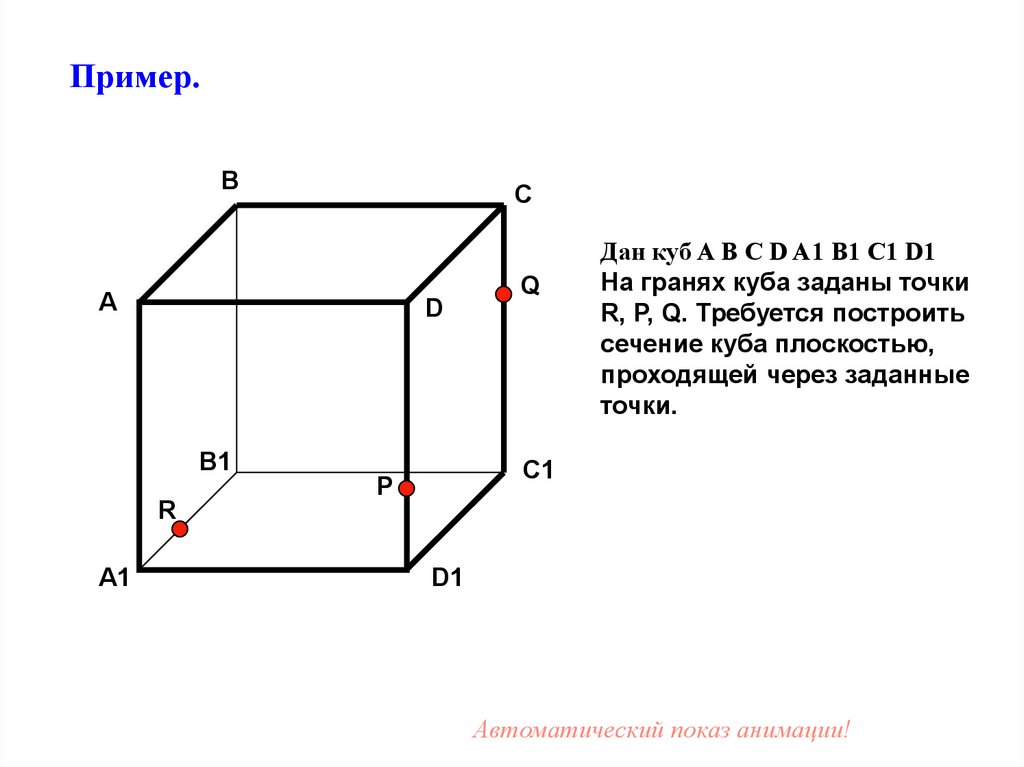
45.

Пример.
В
С
А
D
B1
Q
Дан куб A B C D A1 B1 C1 D1
На гранях куба заданы точки
R, P, Q. Требуется построить
сечение куба плоскостью,
проходящей через заданные
точки.
C1
P
R
A1
D1
Автоматический показ анимации!

46.

В
С
А
D
B1
Q
Точки Р и Q заданы, как
принадлежащие плоскости
сечения. В то же время эти
точки принадлежат плоскости
грани C D D1 C1, следовательно
линия PQ является линий
пересечения этих плоскостей
C1
P
R
A1
D1
Управление докладчиком

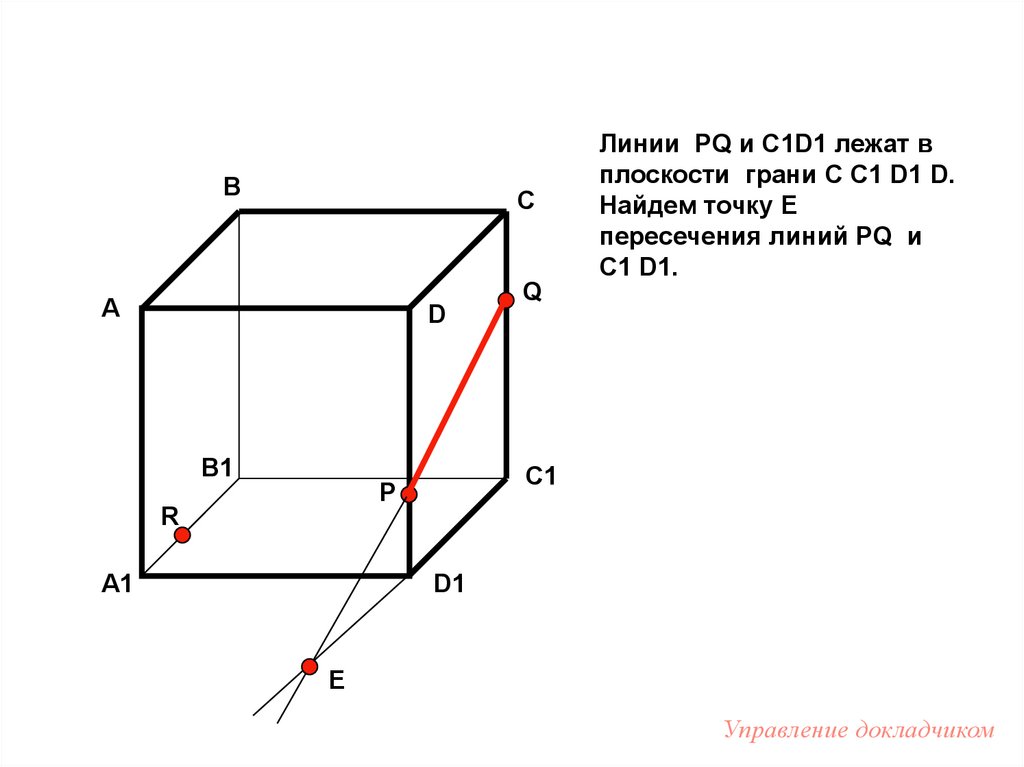
47.

В
С
А
D
B1
Линии PQ и C1D1 лежат в
плоскости грани C C1 D1 D.
Найдем точку Е
пересечения линий PQ и
C1 D1.
Q
C1
P
R
A1
D1
E
Управление докладчиком

48.

В
С
А
D
B1
Q
Точки R и E принадлежат
плоскости сечения
и плоскости основания куба,
следовательно линия RE,
соединяющая эти точки будет
линией пересечения
плоскости сечения и
плоскости основания куба .
C1
P
R
A1
D1
E
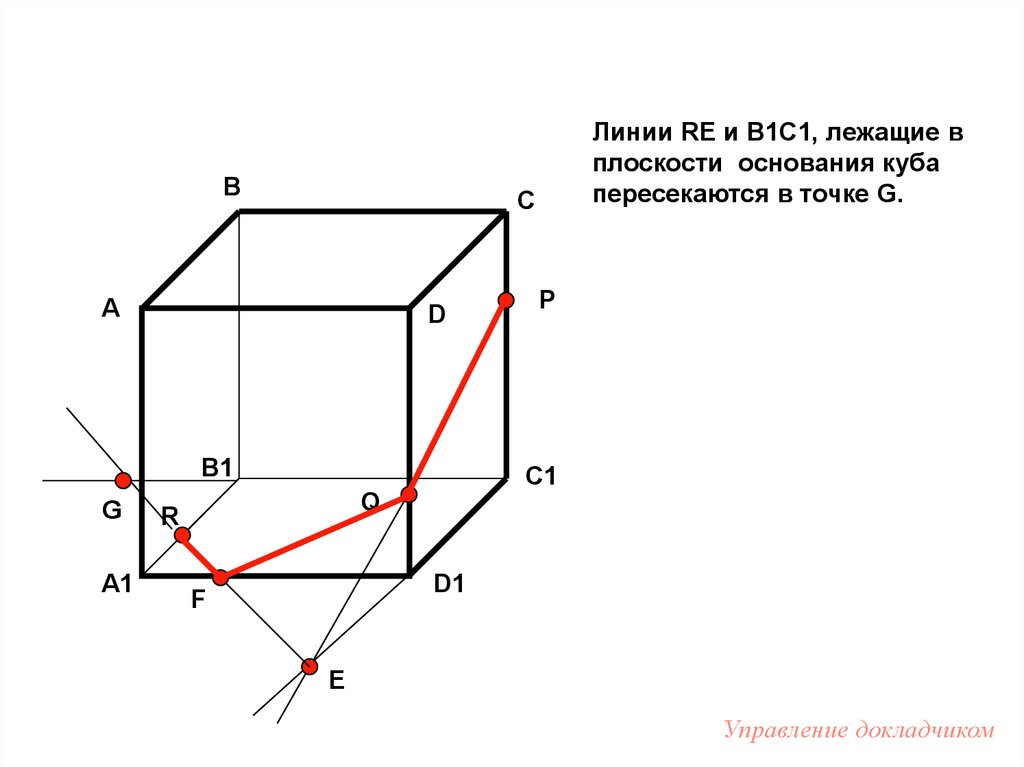
Управление докладчиком

49.

В
С
А
D
B1
RE пересекает A1 D1 в точке F
и линия RF будет линией
пересечения плоскости
сечения и плоскости грани
A1 B1 C1 D1.
Q
C1
P
R
A1
D1
F
E
Управление докладчиком

50.

В
С
А
D
B1
C1
Q
R
A1
P
Точки и Q, и F принадлежат
плоскости сечения
и плоскости грани A A1 D1
D, следовательно линия QF
будет линией пересечения
этих плоскостей.
D1
F
E
Управление докладчиком

51.

В
С
А
D
B1
G
A1
Линии RE и B1C1, лежащие в
плоскости основания куба
пересекаются в точке G.
P
C1
Q
R
D1
F
E
Управление докладчиком

52.

В
С
А
D
B1
G
A1
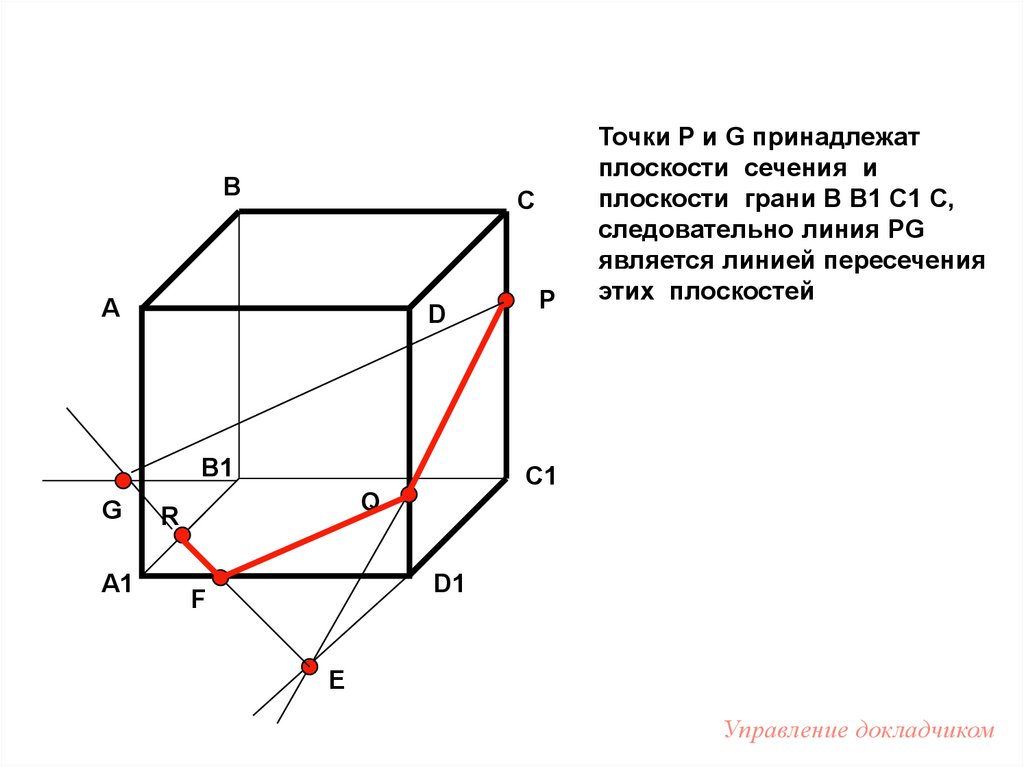
P
Точки P и G принадлежат
плоскости сечения и
плоскости грани B B1 C1 C,
следовательно линия PG
является линией пересечения
этих плоскостей
C1
Q
R
D1
F
E
Управление докладчиком

53.

В
PG пересекает B B1 в точке
H и линия PH будет линией
пересечения плоскости
сечения и плоскости грани
B B1 C1 C.
С
А
D
P
H
B1
G
A1
C1
Q
R
D1
F
E
Управление докладчиком

54.

В
С
А
D
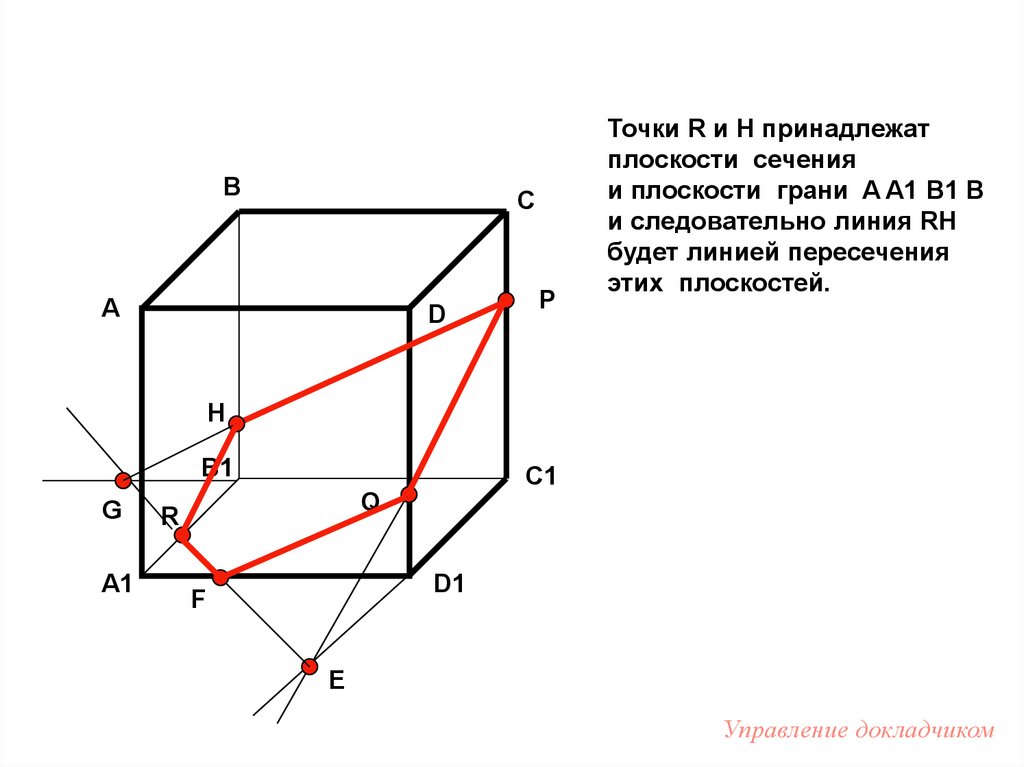
P
Точки R и H принадлежат
плоскости сечения
и плоскости грани A A1 B1 B
и следовательно линия RH
будет линией пересечения
этих плоскостей.
H
B1
G
A1
C1
Q
R
D1
F
E
Управление докладчиком

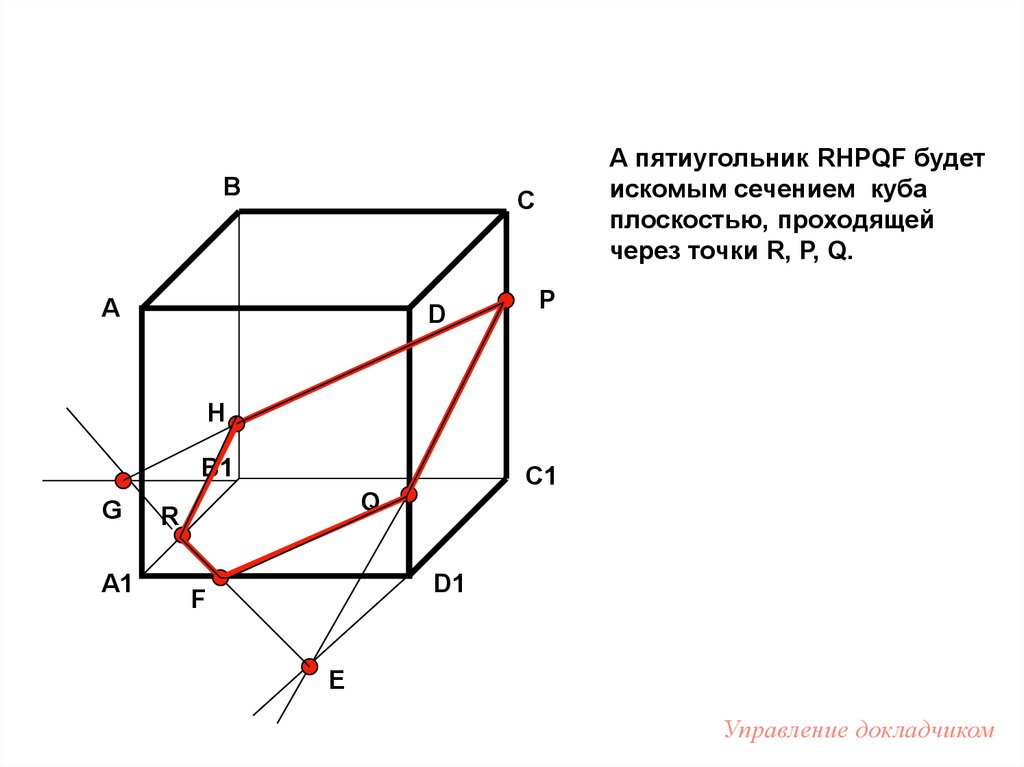
55.

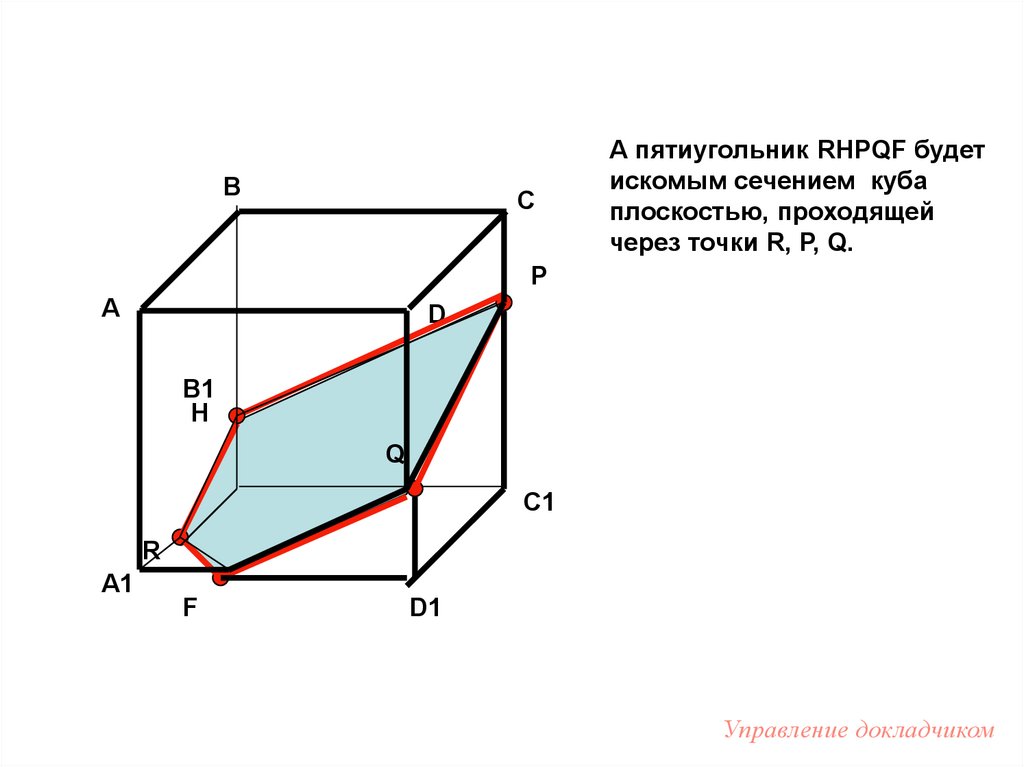
В
А пятиугольник RHPQF будет
искомым сечением куба
плоскостью, проходящей
через точки R, P, Q.
С
А
D
P
H
B1
G
A1
C1
Q
R
D1
F
E
Управление докладчиком

56.

В
С
А пятиугольник RHPQF будет
искомым сечением куба
плоскостью, проходящей
через точки R, P, Q.
P
А
D
B1
H
Q
C1
R
A1
F
D1
Управление докладчиком

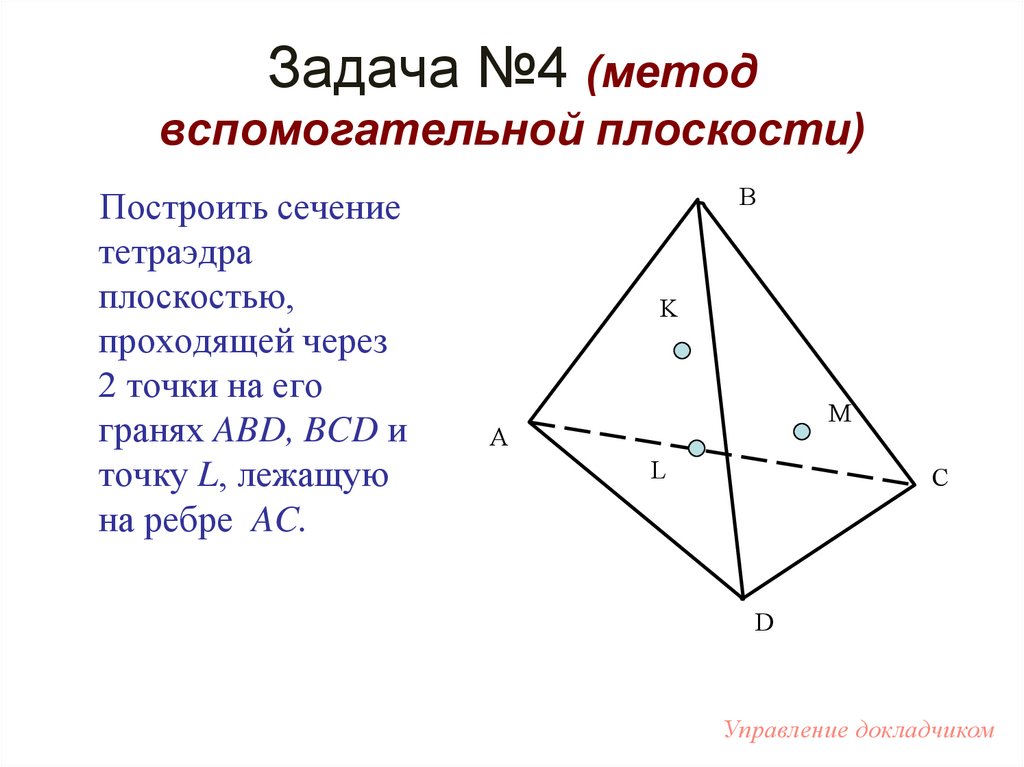
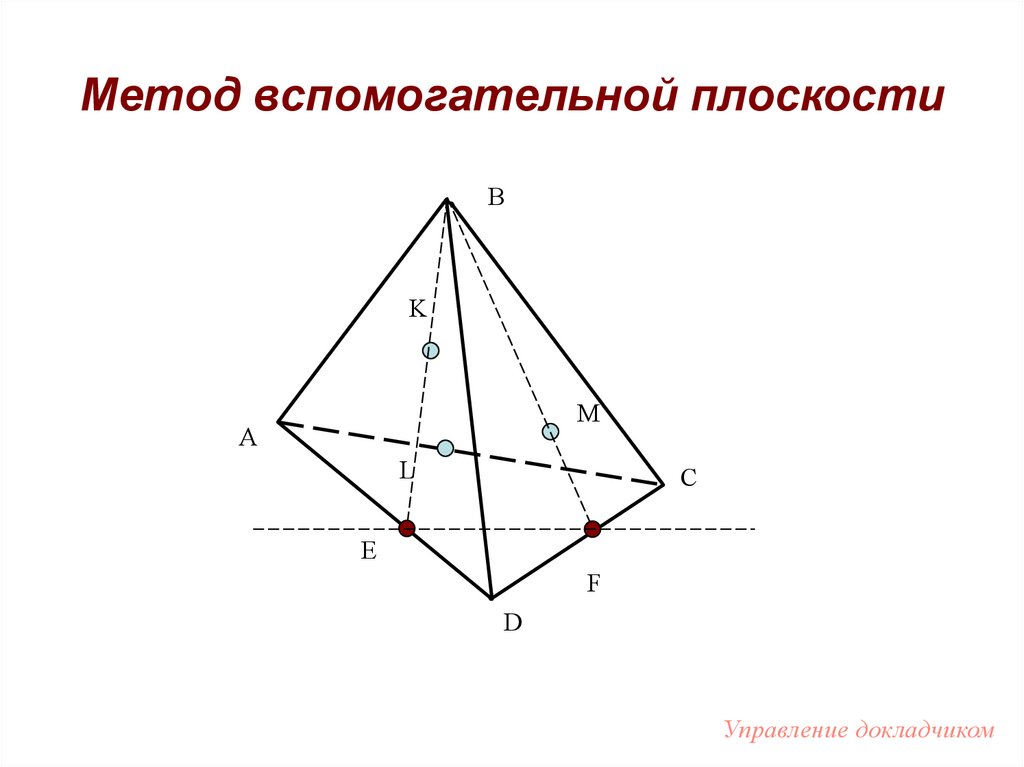
57. Задача №4 (метод вспомогательной плоскости)

Построить сечение
тетраэдра
плоскостью,
проходящей через
2 точки на его
гранях ABD, BCD и
точку L, лежащую
на ребре AC.
B
K
M
A
L
C
D
Управление докладчиком

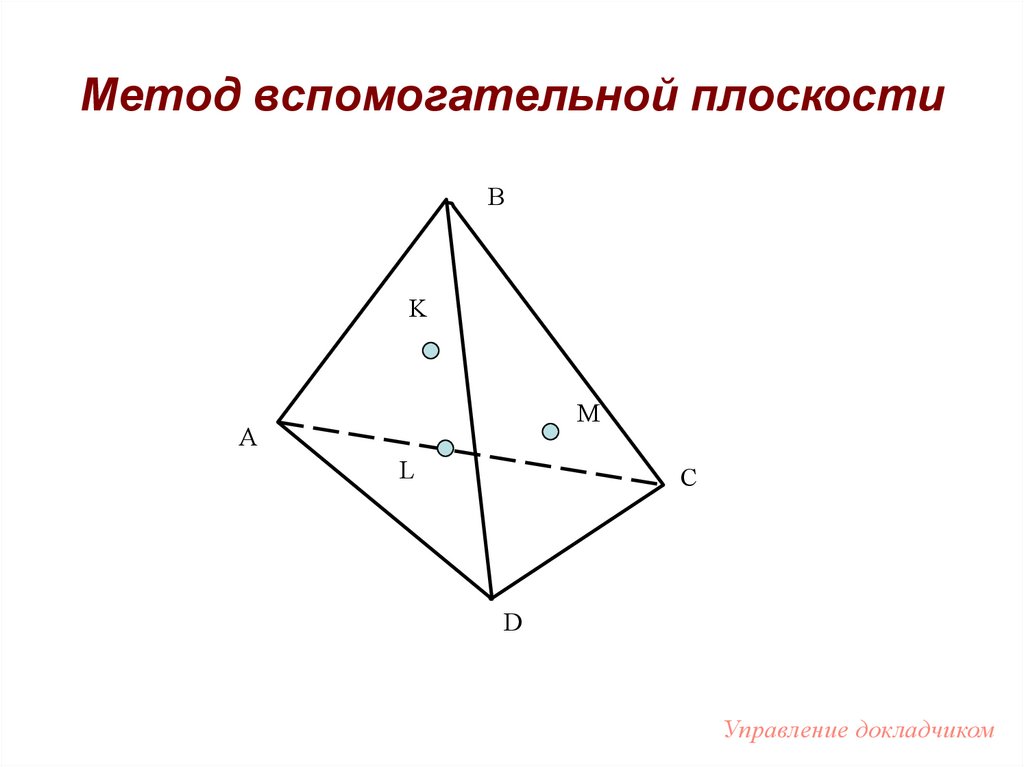
58. Метод вспомогательной плоскости

B
K
M
A
L
C
D
Управление докладчиком

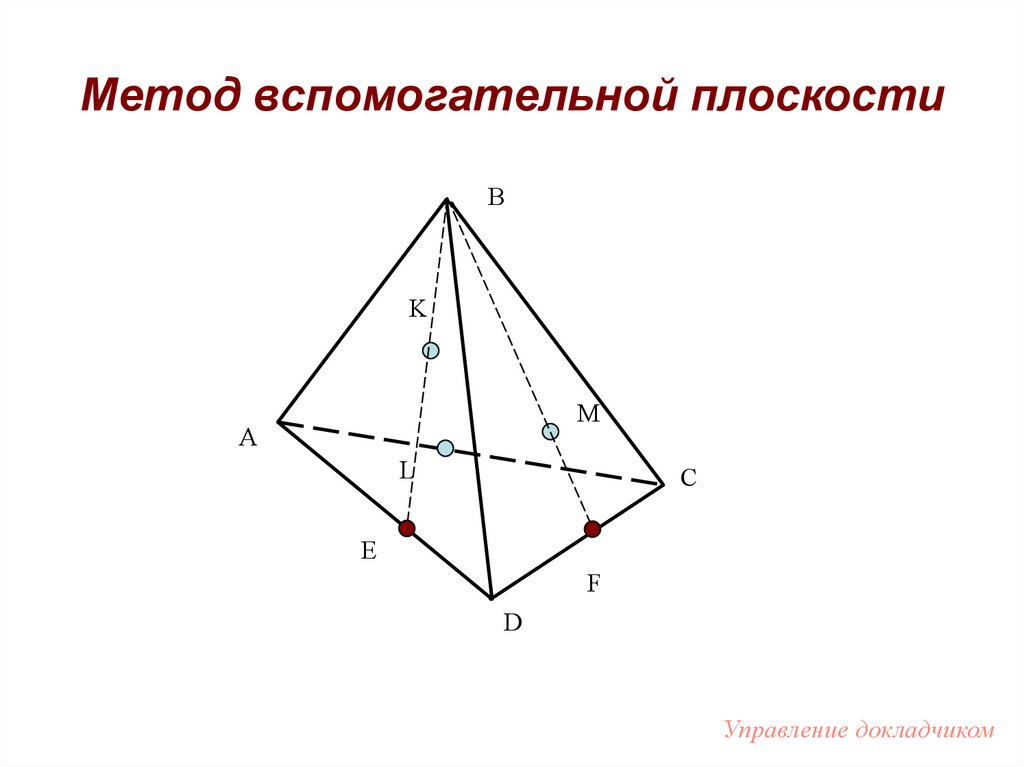
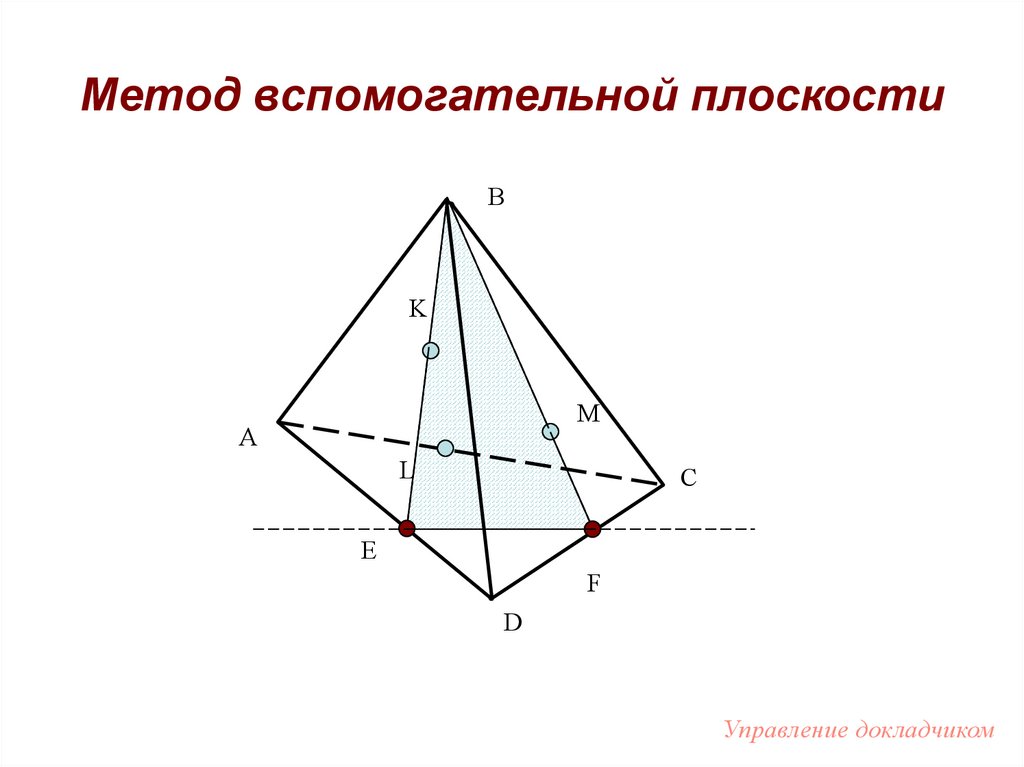
59. Метод вспомогательной плоскости

B
K
M
A
L
C
Е
F
D
Управление докладчиком

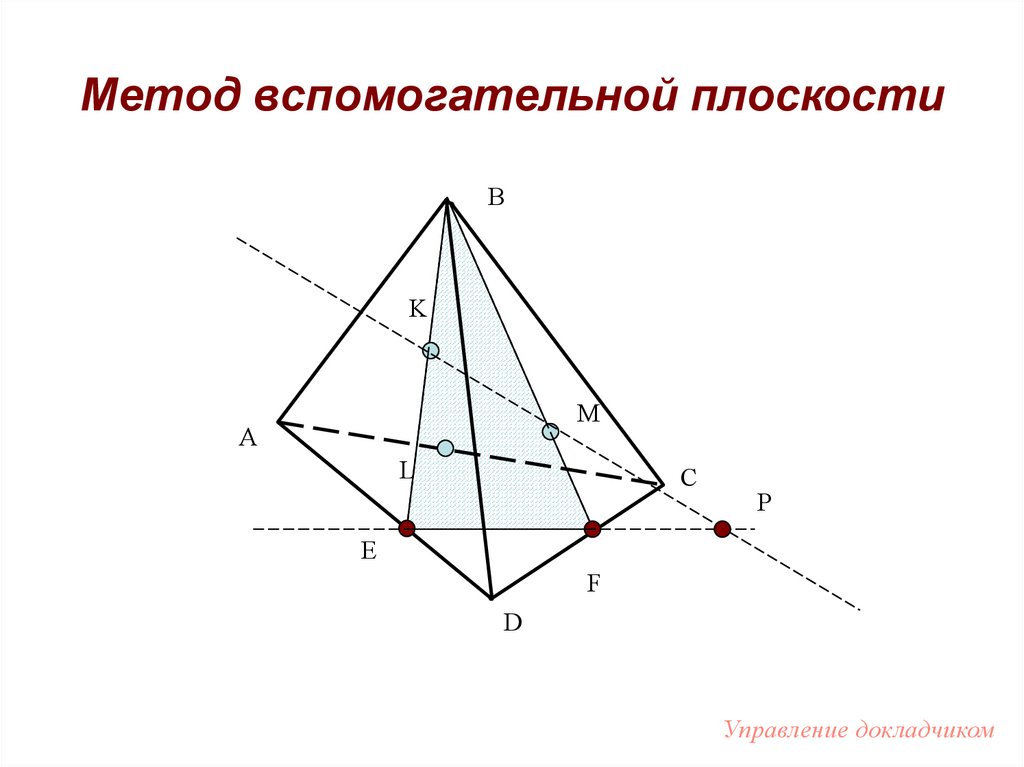
60. Метод вспомогательной плоскости

B
K
M
A
L
C
Е
F
D
Управление докладчиком

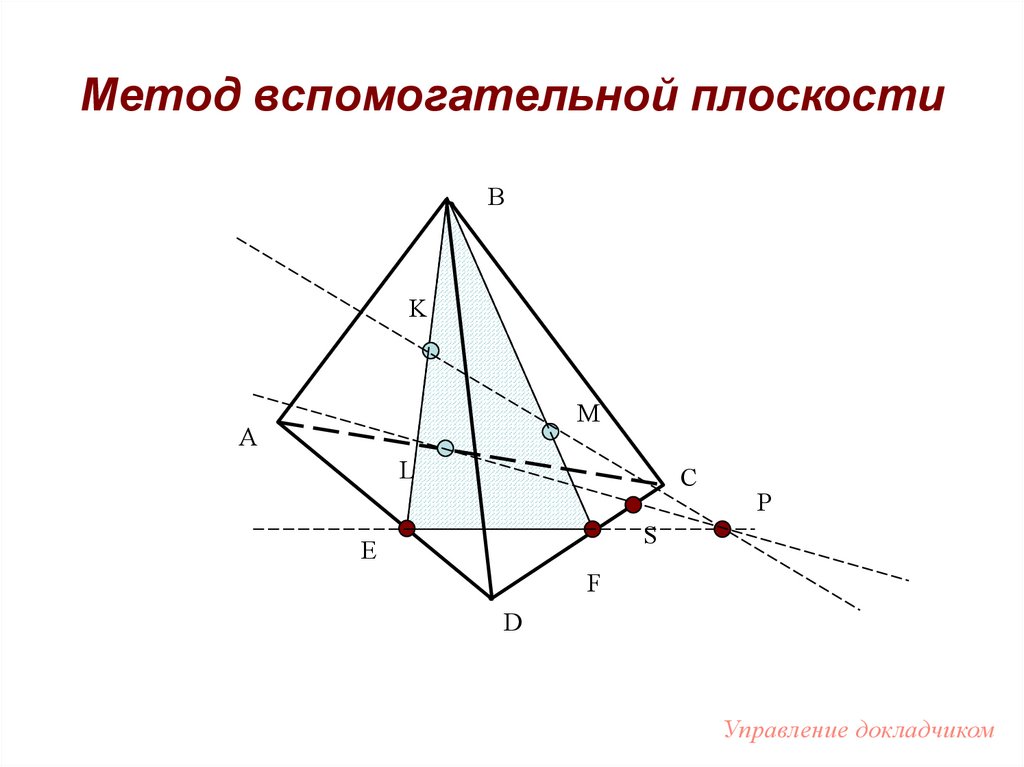
61. Метод вспомогательной плоскости

B
K
M
A
L
C
Е
F
D
Управление докладчиком

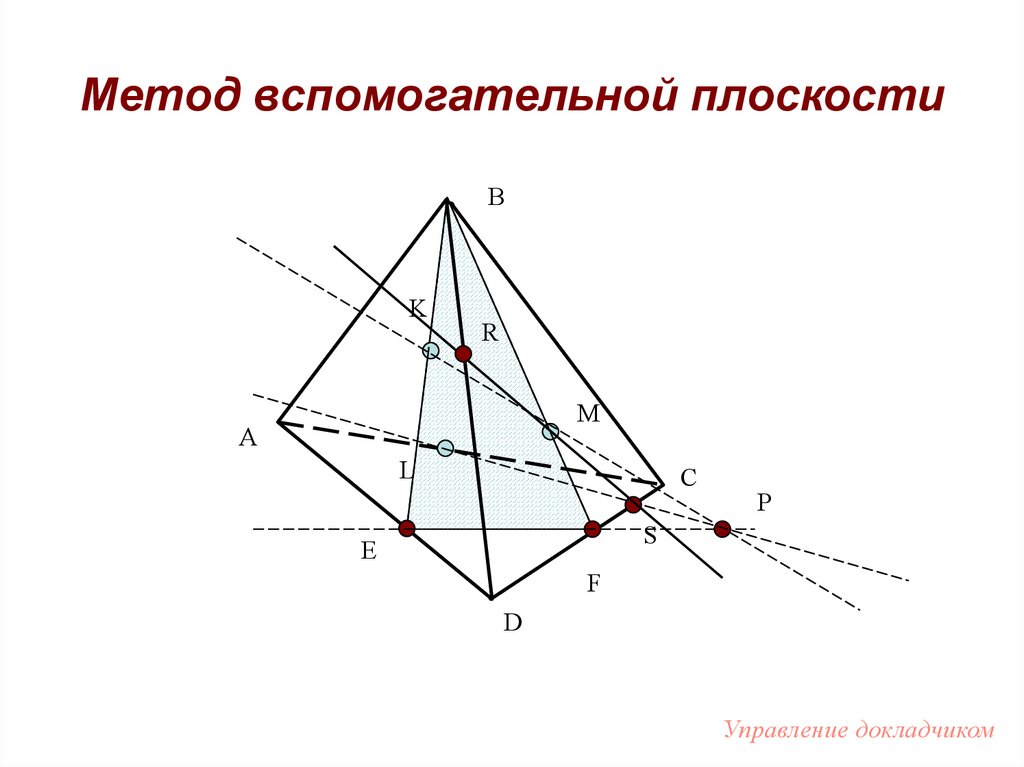
62. Метод вспомогательной плоскости

B
K
M
A
L
C
P
Е
F
D
Управление докладчиком

63. Метод вспомогательной плоскости

B
K
M
A
L
C
P
S
Е
F
D
Управление докладчиком

64. Метод вспомогательной плоскости

B
K
R
M
A
L
C
P
S
Е
F
D
Управление докладчиком

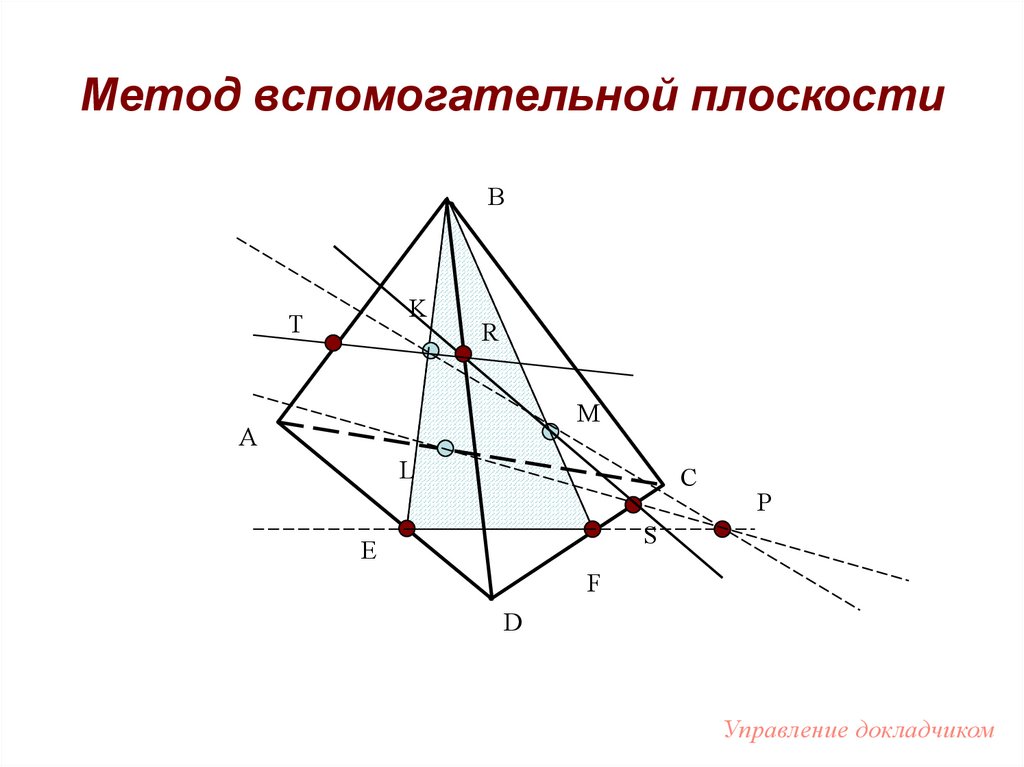
65. Метод вспомогательной плоскости

B
K
T
R
M
A
L
C
P
S
Е
F
D
Управление докладчиком

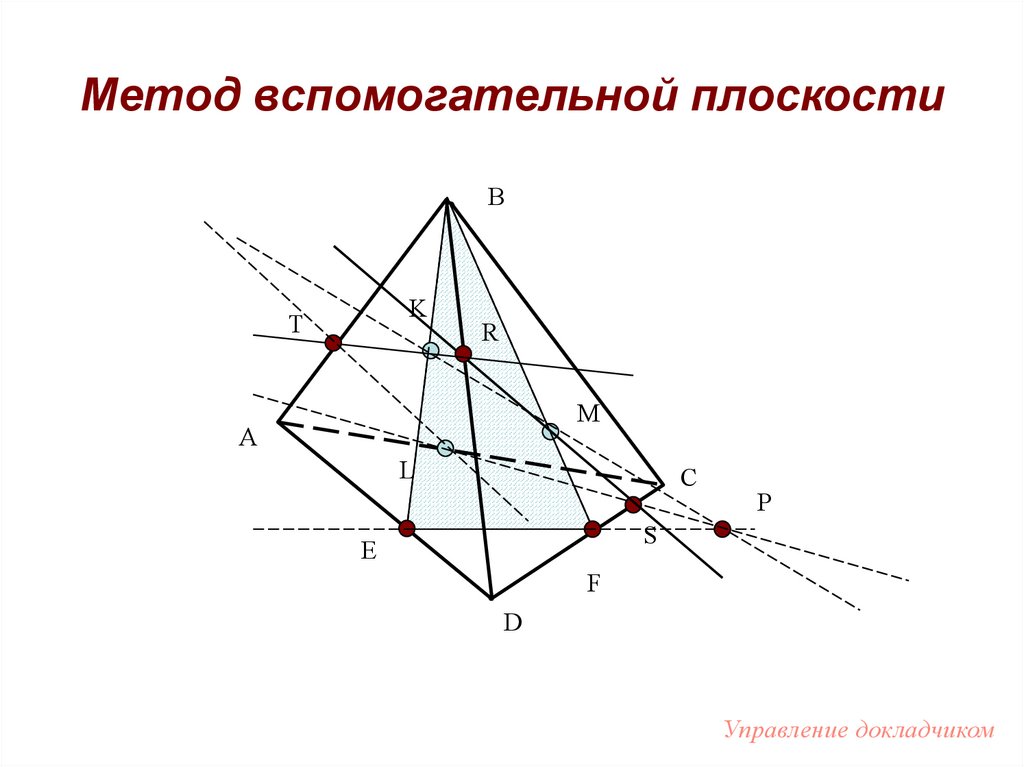
66. Метод вспомогательной плоскости

B
K
T
R
M
A
L
C
P
S
Е
F
D
Управление докладчиком

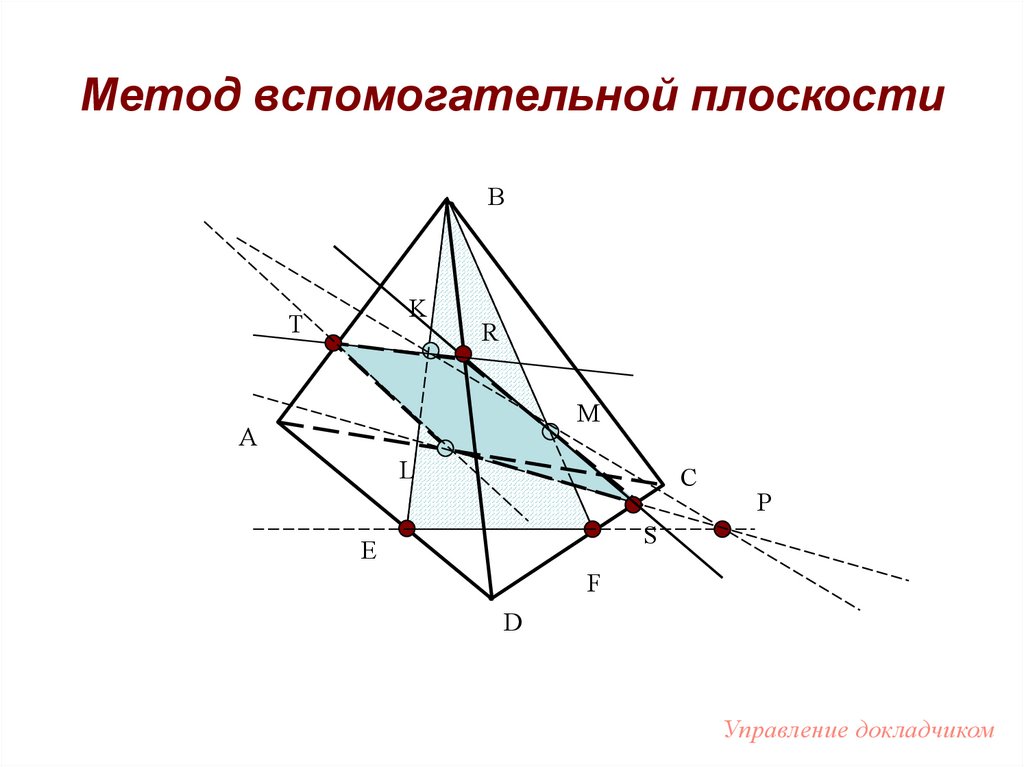
67. Метод вспомогательной плоскости

B
K
T
R
M
A
L
C
P
S
Е
F
D
Управление докладчиком

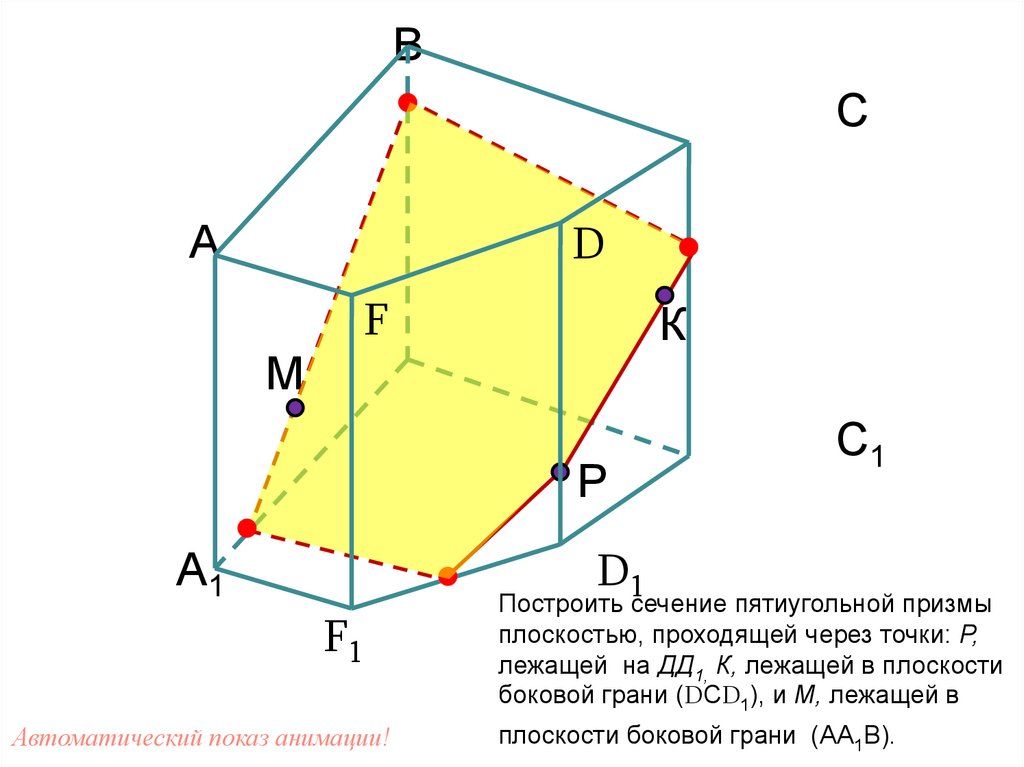
68.

Задача №5 (метод внутреннего
проектирования)
Построить сечение
пятиугольной призмы
плоскостью, проходящей через
точки: Р, лежащей на ДД1, К,
лежащей в плоскости боковой
грани (DСD1), и М, лежащей в
плоскости боковой грани
(АА1В).
Управление докладчиком

69.

Метод внутреннего проектирования
Построить сечение пятиугольной
призмы плоскостью, проходящей
через точки: Р, лежащей на ДД1, К,
лежащей в плоскости боковой
грани (DСD1), и М, лежащей в
Автоматический показ анимации!
плоскости боковой грани (АА1В).

70.

В
С
А
D
К
F
М
Р
А1
С1
D1
F1
Автоматический показ анимации!
Построить сечение пятиугольной призмы
плоскостью, проходящей через точки: Р,
лежащей на ДД1, К, лежащей в плоскости
боковой грани (DСD1), и М, лежащей в
плоскости боковой грани (АА1В).

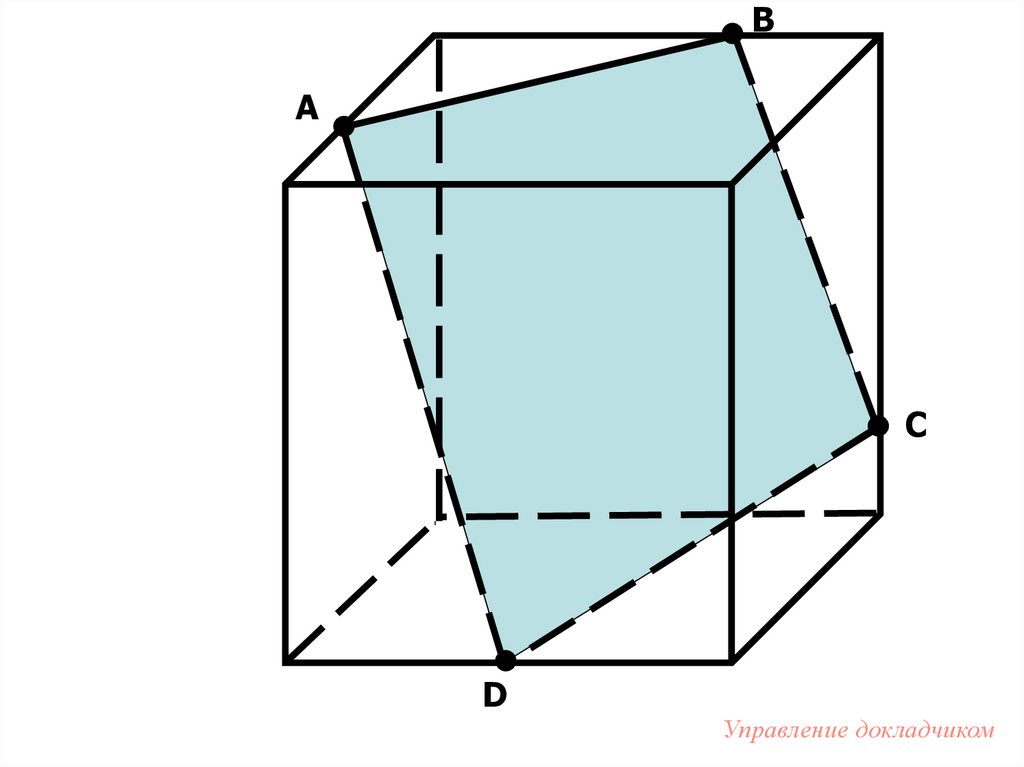
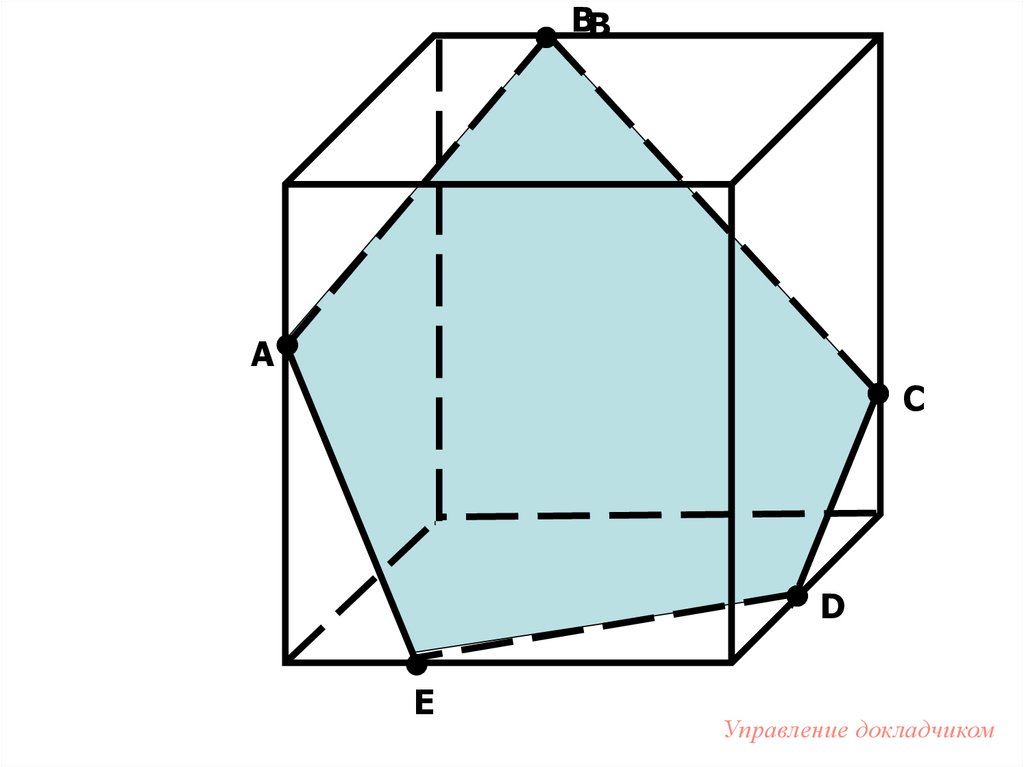
71. Найдите ошибку

• Правильно ли построены эти
сечения? Если нет, объясните
почему.
Управление докладчиком

72.

B
А
C
D
Управление докладчиком

73.

C
D
B
A
E
F
Управление докладчиком

74.

BB
A
C
D
E
Управление докладчиком

75.

Задание
В1
С1
Е
А1
D1
F
C
B
A
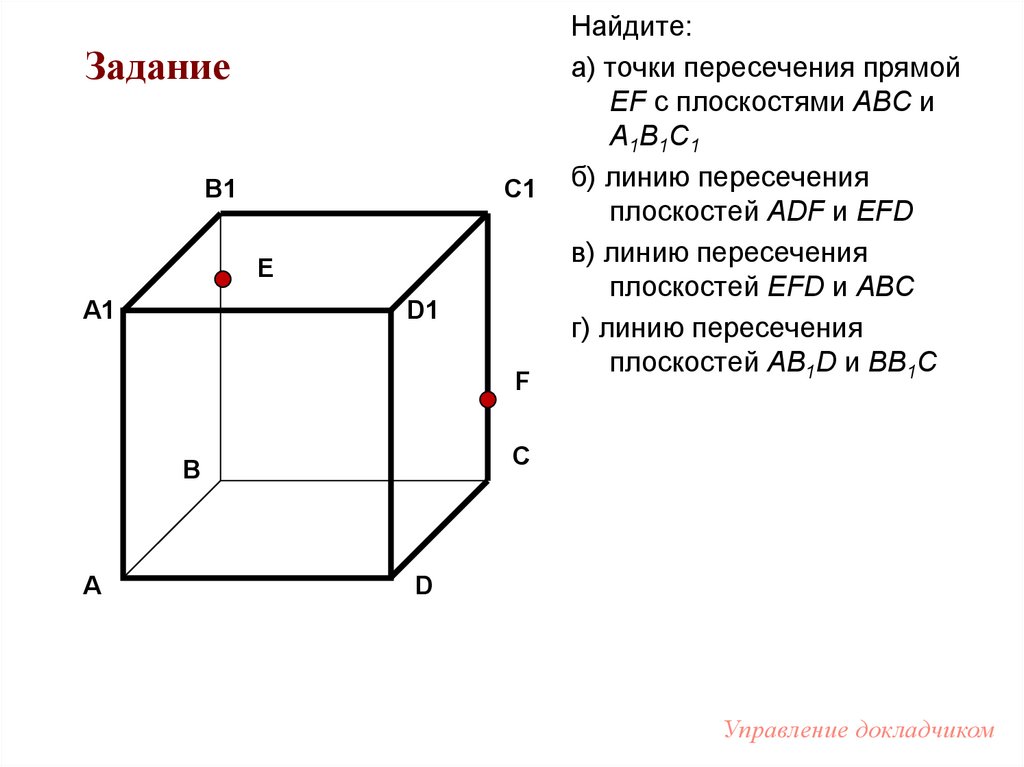
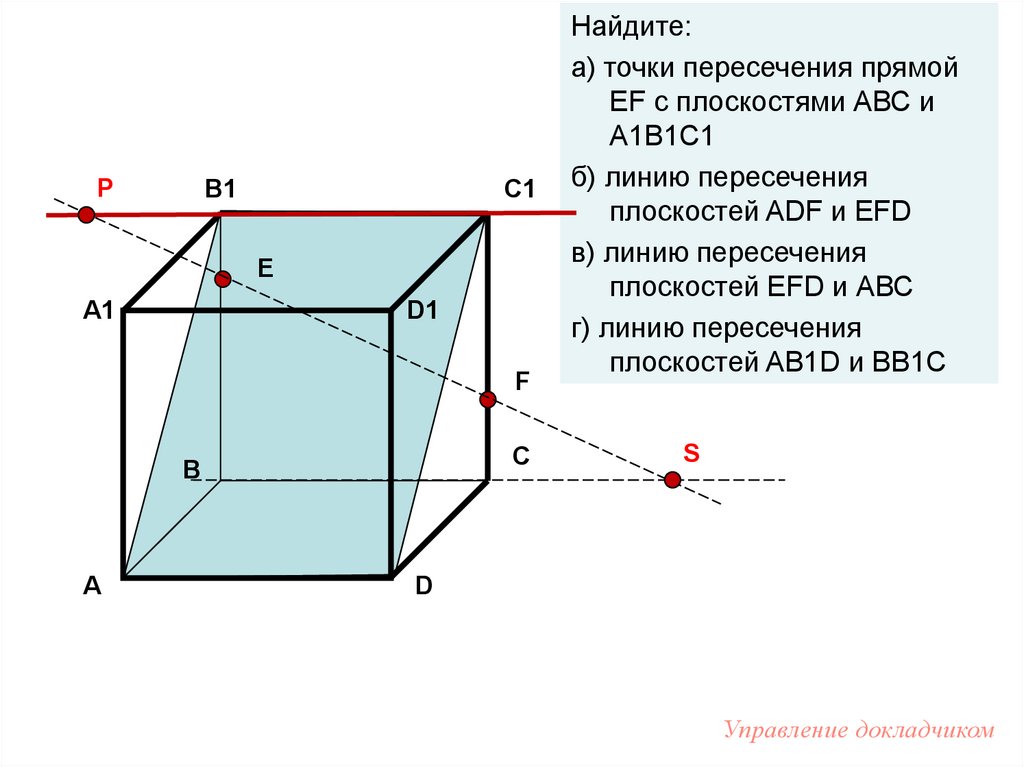
Найдите:
а) точки пересечения прямой
EF с плоскостями АВС и
А1В1С1
б) линию пересечения
плоскостей ADF и EFD
в) линию пересечения
плоскостей EFD и АВС
г) линию пересечения
плоскостей AB1D и BB1C
D
Управление докладчиком

76.

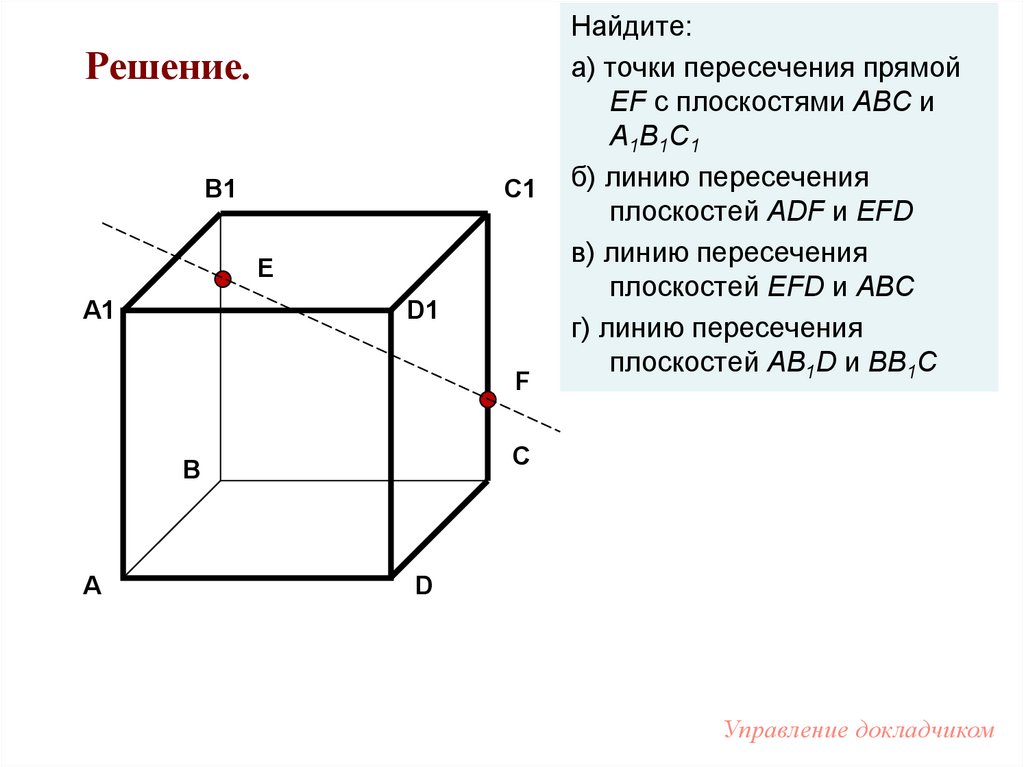
Решение.
В1
С1
Е
А1
D1
F
C
B
A
Найдите:
а) точки пересечения прямой
EF с плоскостями АВС и
А1В1С1
б) линию пересечения
плоскостей ADF и EFD
в) линию пересечения
плоскостей EFD и АВС
г) линию пересечения
плоскостей AB1D и BB1C
D
Управление докладчиком

77.

В1
С1
Е
А1
D1
F
C
B
A
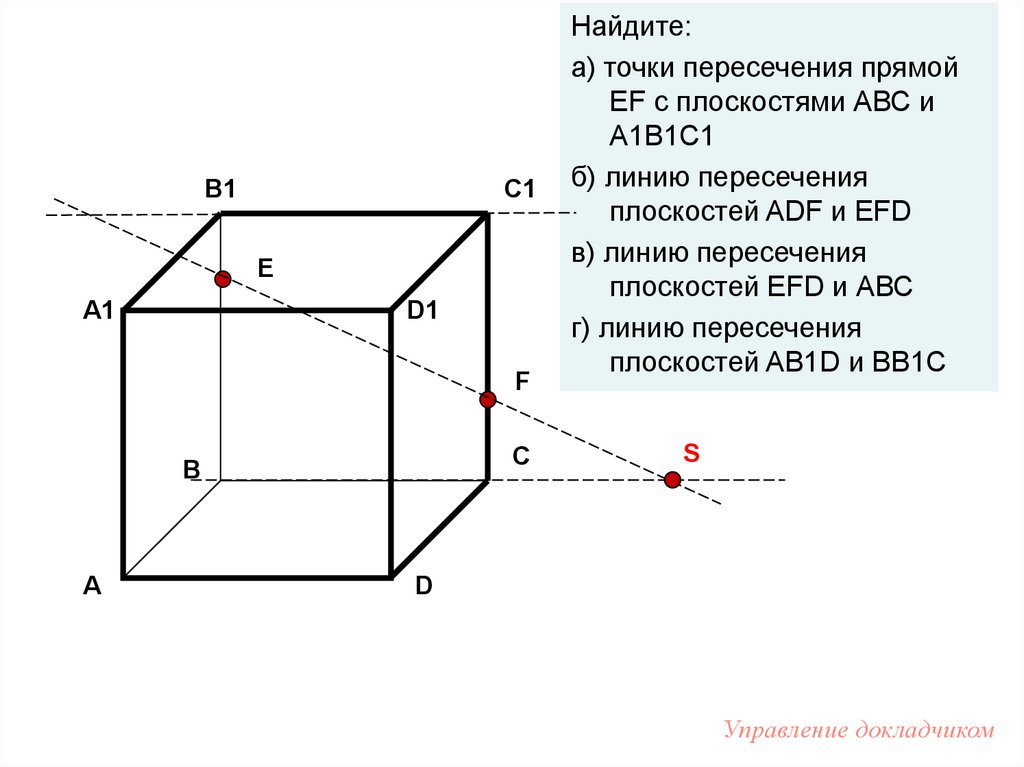
Найдите:
а) точки пересечения прямой
EF с плоскостями АВС и
А1В1С1
б) линию пересечения
плоскостей ADF и EFD
в) линию пересечения
плоскостей EFD и АВС
г) линию пересечения
плоскостей AB1D и BB1C
D
Управление докладчиком

78.

В1
С1
Е
А1
D1
F
C
B
A
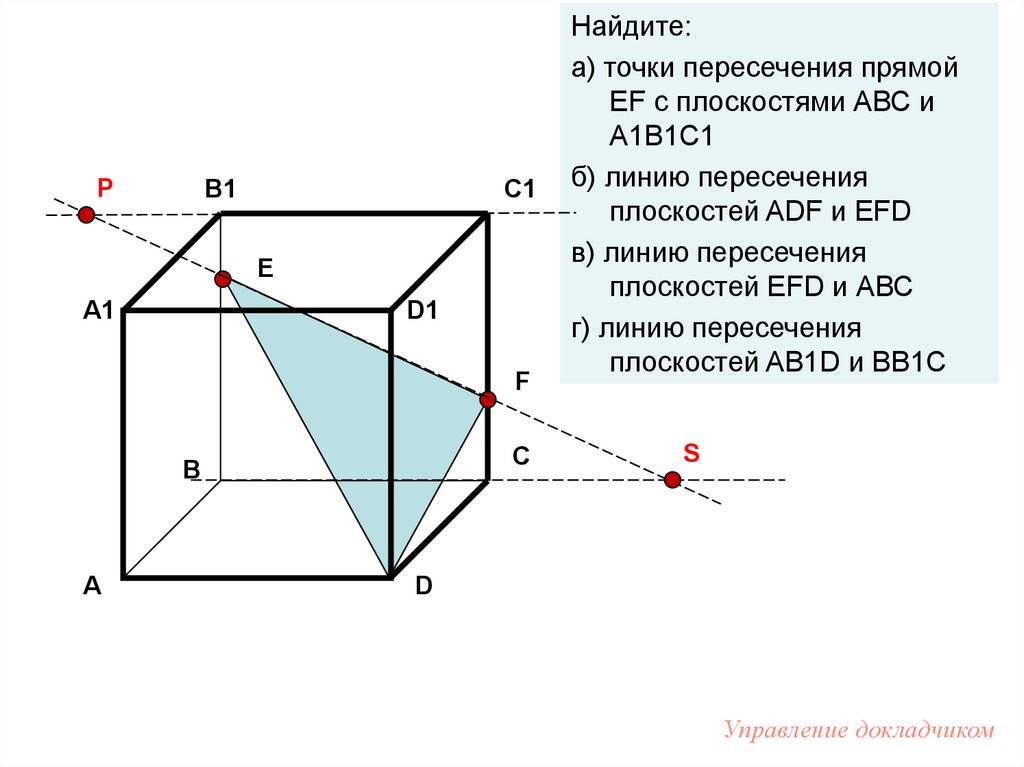
Найдите:
а) точки пересечения прямой
EF с плоскостями АВС и
А1В1С1
б) линию пересечения
плоскостей ADF и EFD
в) линию пересечения
плоскостей EFD и АВС
г) линию пересечения
плоскостей AB1D и BB1C
S
D
Управление докладчиком

79.

В1
С1
Е
А1
D1
F
C
B
A
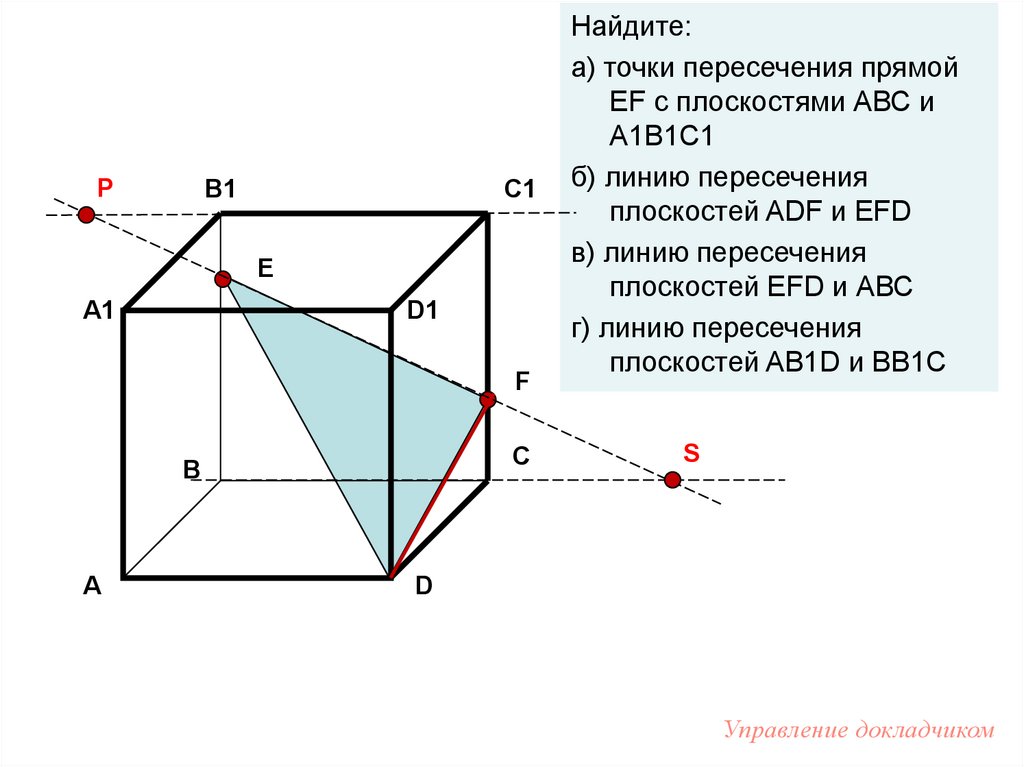
Найдите:
а) точки пересечения прямой
EF с плоскостями АВС и
А1В1С1
б) линию пересечения
плоскостей ADF и EFD
в) линию пересечения
плоскостей EFD и АВС
г) линию пересечения
плоскостей AB1D и BB1C
S
D
Управление докладчиком

80.

В1
P
С1
Е
А1
D1
F
C
B
A
Найдите:
а) точки пересечения прямой
EF с плоскостями АВС и
А1В1С1
б) линию пересечения
плоскостей ADF и EFD
в) линию пересечения
плоскостей EFD и АВС
г) линию пересечения
плоскостей AB1D и BB1C
S
D
Управление докладчиком

81.

В1
P
С1
Е
А1
D1
F
C
B
A
Найдите:
а) точки пересечения прямой
EF с плоскостями АВС и
А1В1С1
б) линию пересечения
плоскостей ADF и EFD
в) линию пересечения
плоскостей EFD и АВС
г) линию пересечения
плоскостей AB1D и BB1C
S
D
Управление докладчиком

82.

В1
P
С1
Е
А1
D1
F
C
B
A
Найдите:
а) точки пересечения прямой
EF с плоскостями АВС и
А1В1С1
б) линию пересечения
плоскостей ADF и EFD
в) линию пересечения
плоскостей EFD и АВС
г) линию пересечения
плоскостей AB1D и BB1C
S
D
Управление докладчиком

83.

В1
P
С1
Е
А1
D1
F
C
B
A
Найдите:
а) точки пересечения прямой
EF с плоскостями АВС и
А1В1С1
б) линию пересечения
плоскостей ADF и EFD
в) линию пересечения
плоскостей EFD и АВС
г) линию пересечения
плоскостей AB1D и BB1C
S
D
Управление докладчиком

84.

В1
P
С1
Е
А1
D1
F
C
B
A
Найдите:
а) точки пересечения прямой
EF с плоскостями АВС и
А1В1С1
б) линию пересечения
плоскостей ADF и EFD
в) линию пересечения
плоскостей EFD и АВС
г) линию пересечения
плоскостей AB1D и BB1C
S
D
Управление докладчиком

85.

В1
P
С1
Е
А1
D1
F
C
B
A
Найдите:
а) точки пересечения прямой
EF с плоскостями АВС и
А1В1С1
б) линию пересечения
плоскостей ADF и EFD
в) линию пересечения
плоскостей EFD и АВС
г) линию пересечения
плоскостей AB1D и BB1C
S
D
Управление докладчиком

86.

В1
P
С1
Е
А1
D1
F
C
B
A
Найдите:
а) точки пересечения прямой
EF с плоскостями АВС и
А1В1С1
б) линию пересечения
плоскостей ADF и EFD
в) линию пересечения
плоскостей EFD и АВС
г) линию пересечения
плоскостей AB1D и BB1C
S
D
Управление докладчиком

87. Решите задачу

• Все грани параллелепипеда – равные
ромбы со стороной а см и острым углом
60 .
а) Постройте сечение параллелепипеда
плоскостью, проходящей через точки В,
D и М, если М – середина ребра В1С1.
б) Докажите, что построенное сечение –
равнобедренная трапеция.
в) Найдите стороны трапеции.
Управление докладчиком

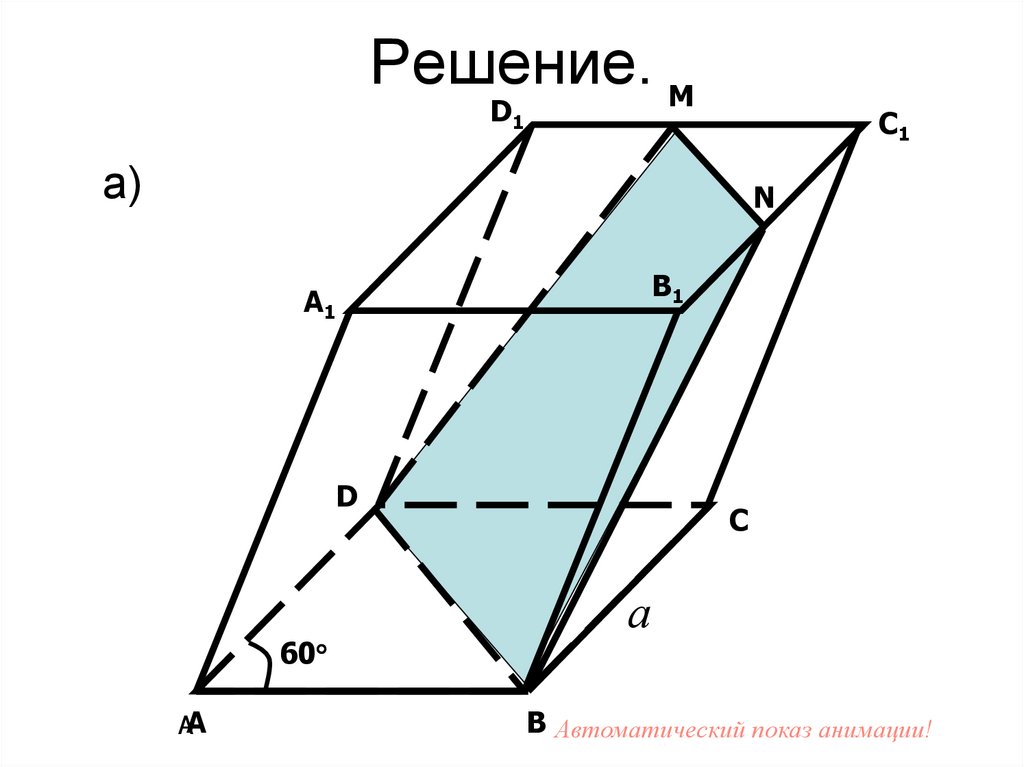
88. Решение.

M
D1
С1
а)
N
В1
А1
D
60
АА
С
а
В Автоматический показ анимации!

89.

б) Пусть – секущая плоскость,
АВСD = ВD, ВСС1В1 = ВМ, МN ВD.
Сечение – трапеция ВDNМ.
ВВ1М = DD1N (ВВ1 = DD1, В1М = D1N,
В1 = D1)
Следовательно, ВМ = DN, значит,
трапеция ВDNМ – равнобедренная.
а 7
а
в) ВD = а см, МN = см, ВМ =
см.
2
2
Управление докладчиком

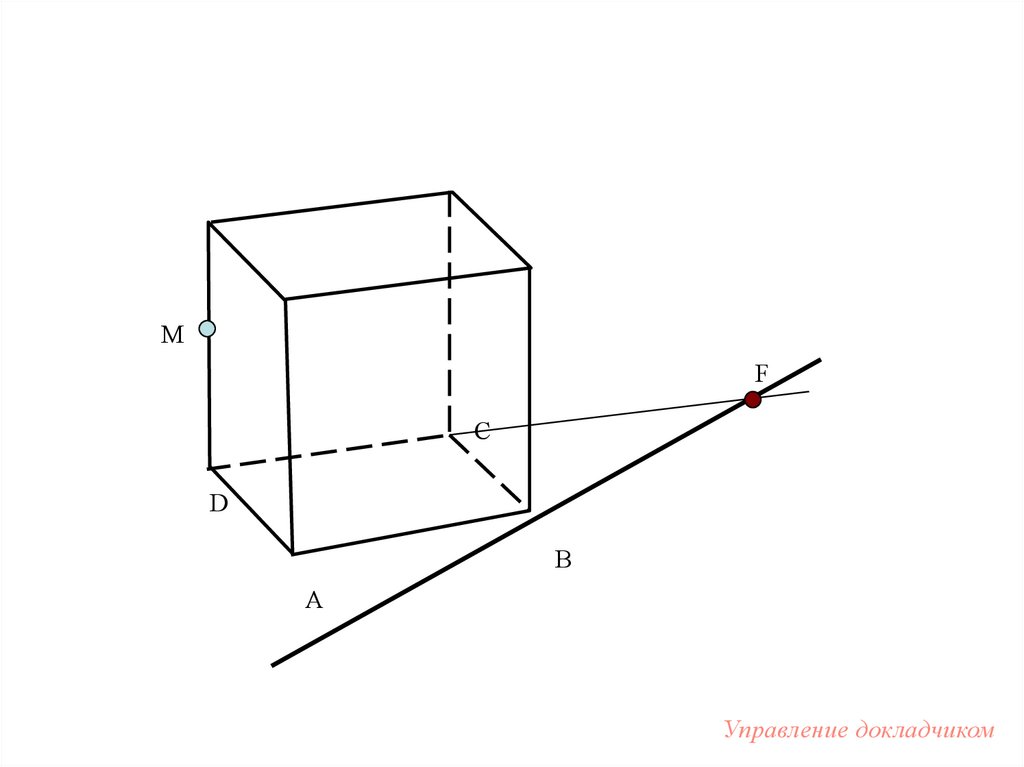
90.

Задача.
Построить сечение
куба плоскостью,
проходящей через точку
на его ребре и прямую,
лежащую в плоскости
нижнего основания.
M
C
D
B
A
Управление докладчиком

91.

M
C
D
B
A
Управление докладчиком

92.

M
F
C
D
B
A
Управление докладчиком

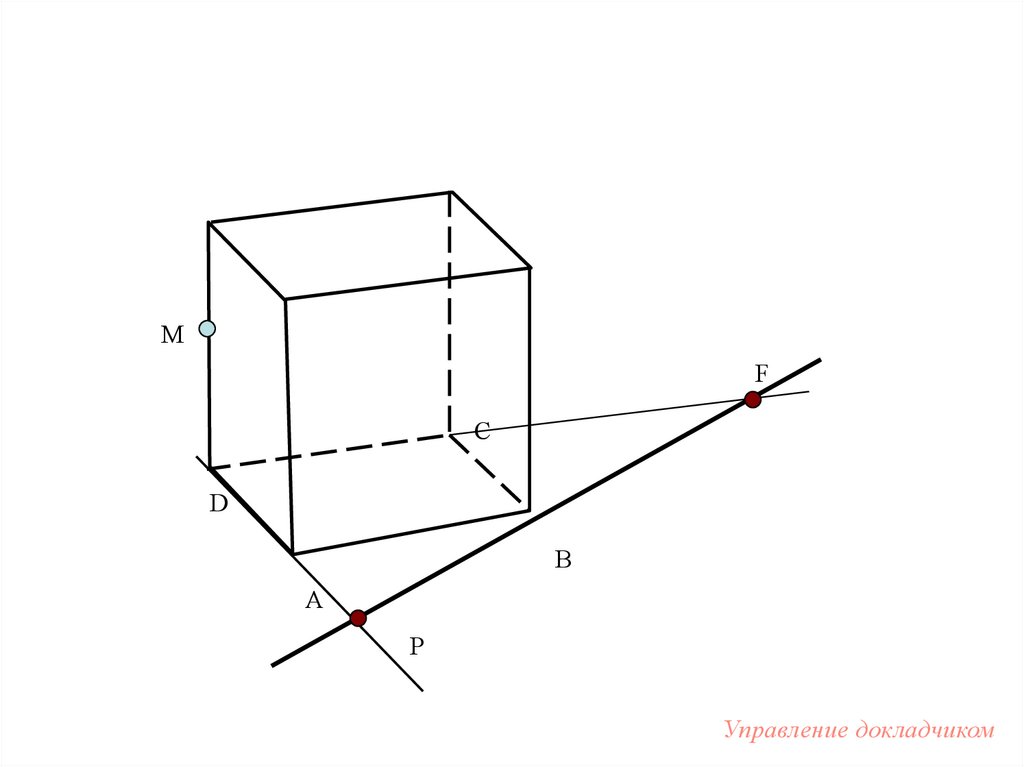
93.

M
F
C
D
B
A
P
Управление докладчиком

94.

K
M
F
C
D
B
A
P
Управление докладчиком

95.

K
M
F
C
D
N
B
A
P
Управление докладчиком

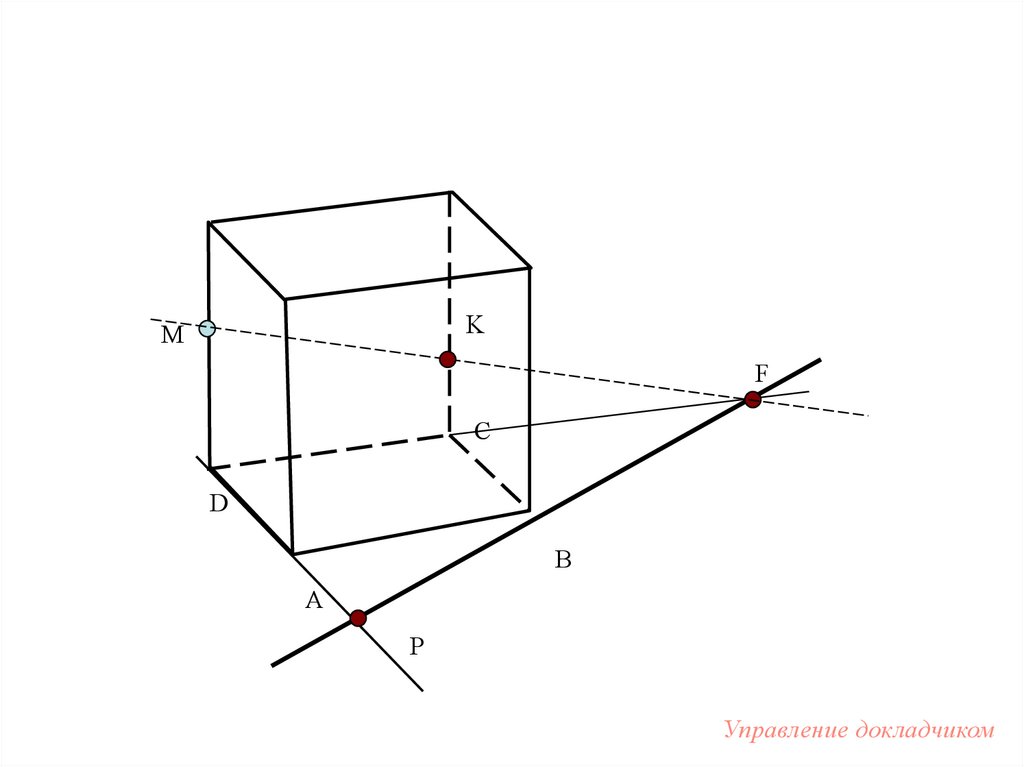
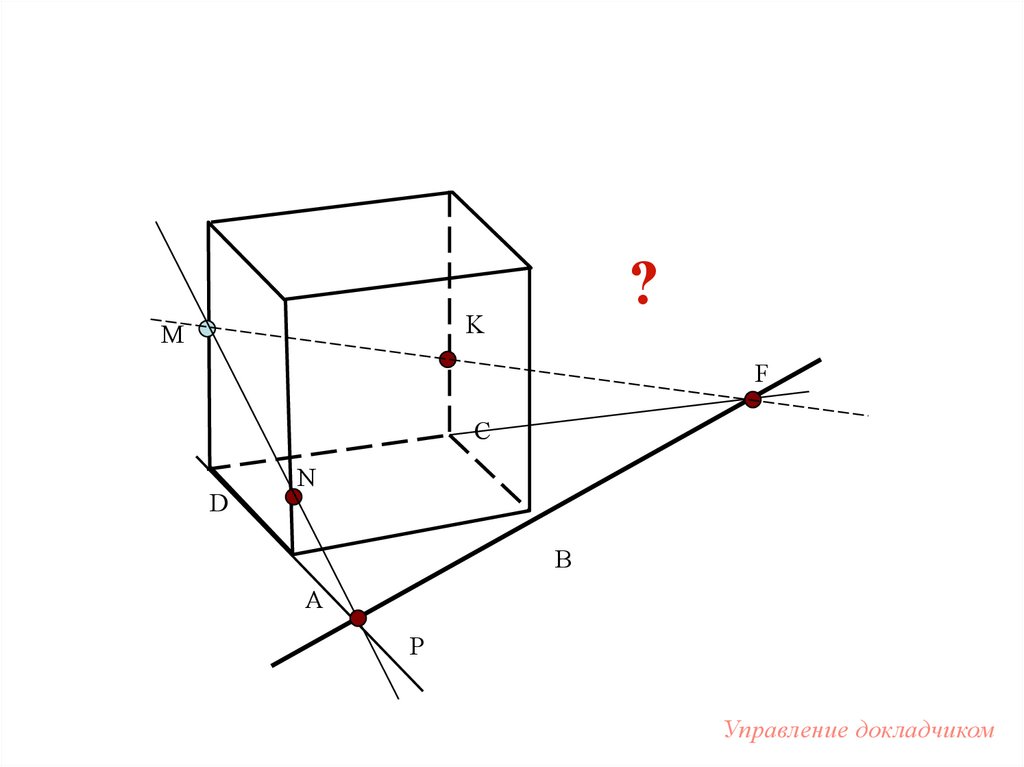
96.

?
K
M
F
C
D
N
B
A
P
Управление докладчиком

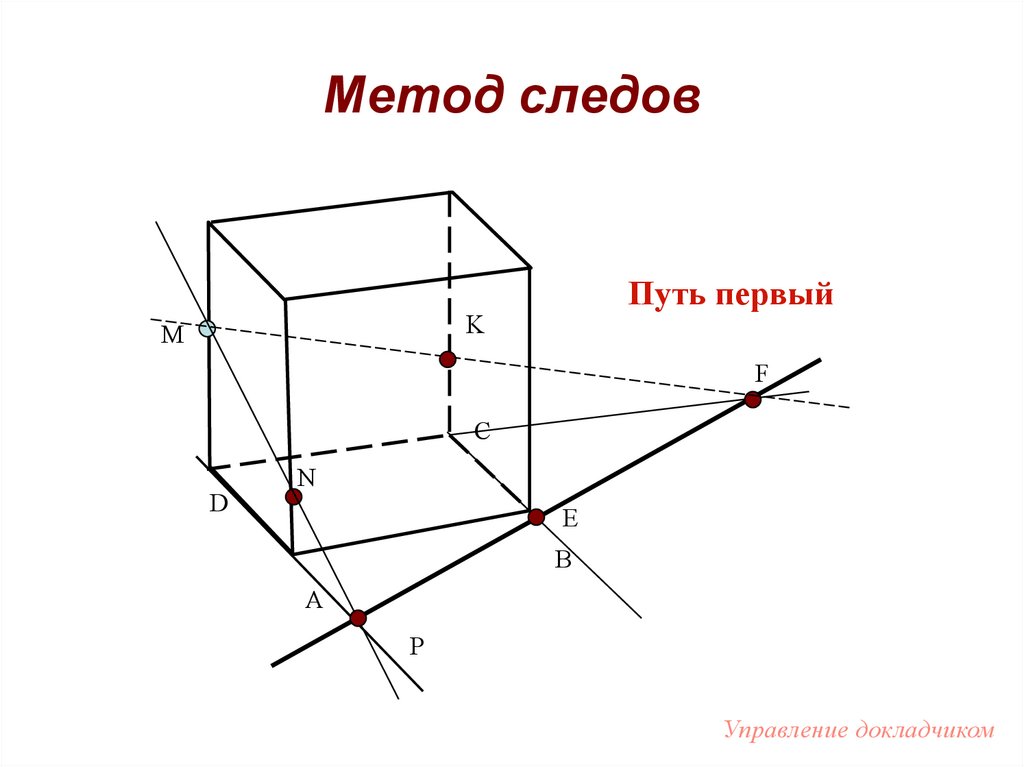
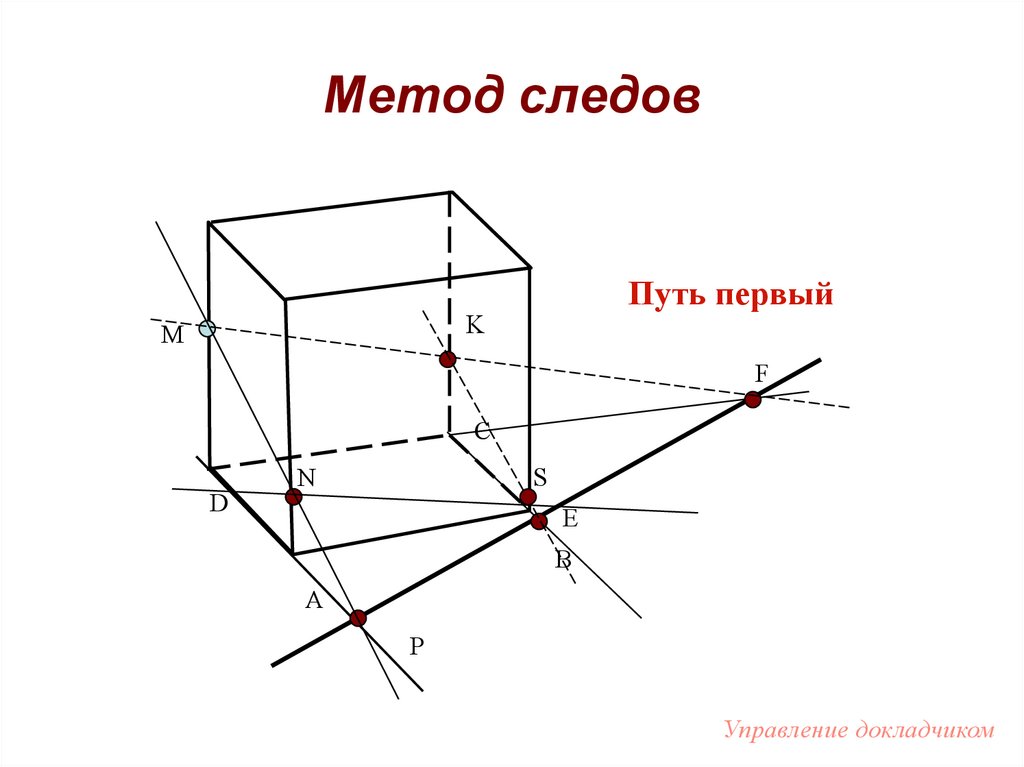
97. Метод следов

Путь первый
K
M
F
C
D
N
E
B
A
P
Управление докладчиком

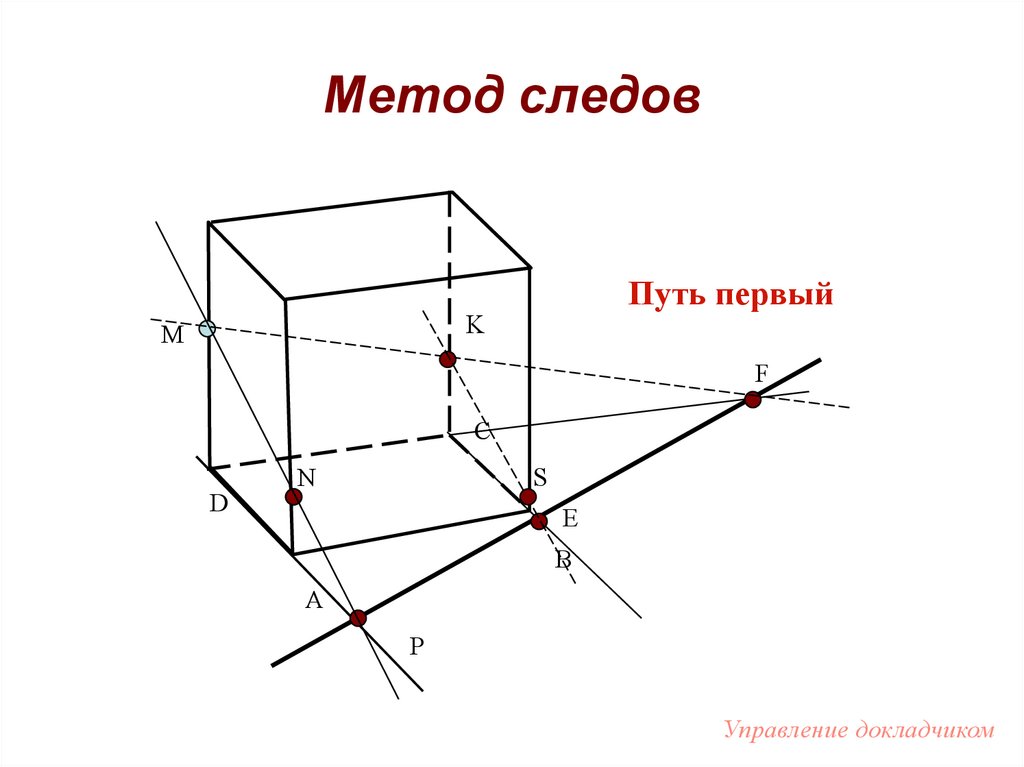
98. Метод следов

Путь первый
K
M
F
C
D
S
N
E
B
A
P
Управление докладчиком

99. Метод следов

Путь первый
K
M
F
C
D
S
N
E
B
A
P
Управление докладчиком

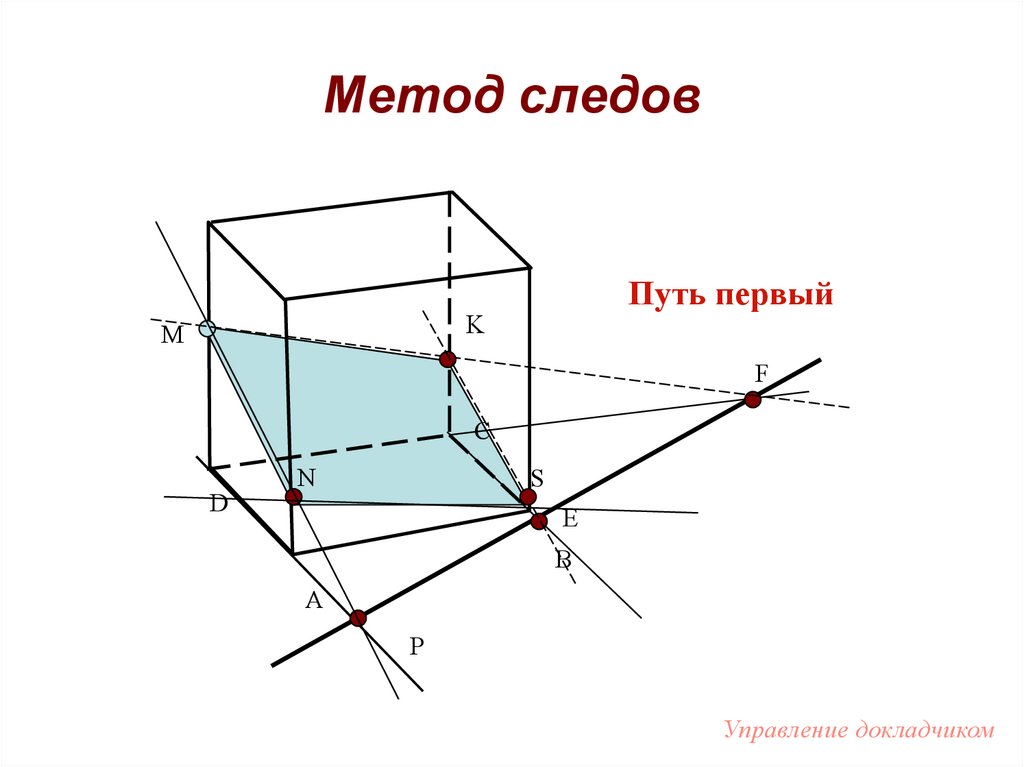
100. Метод следов

Путь первый
K
M
F
C
D
N
S
E
B
A
P
Управление докладчиком

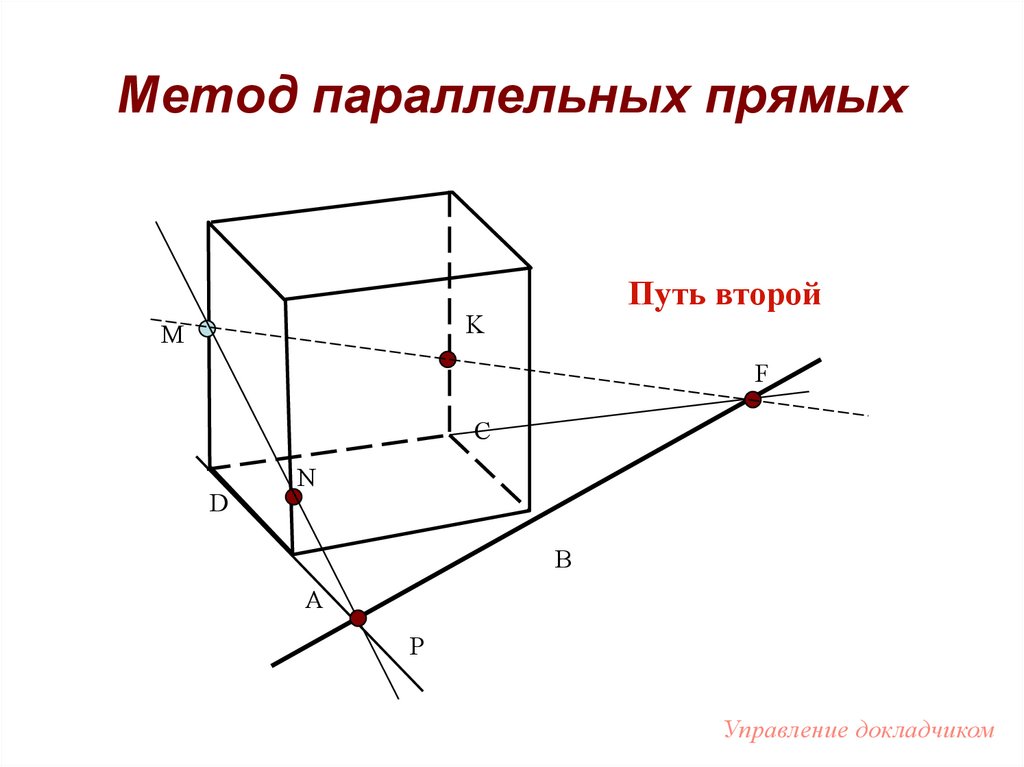
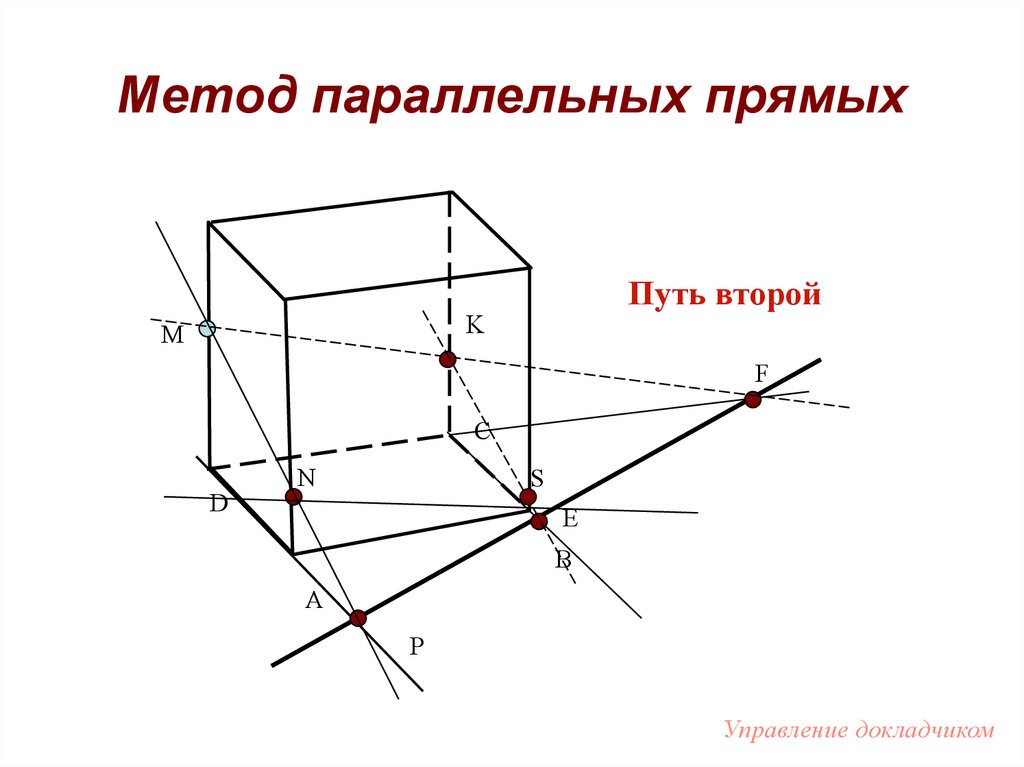
101. Метод параллельных прямых

Путь второй
K
M
F
C
D
N
B
A
P
Управление докладчиком

102.

Метод параллельных прямых
Путь второй
K
M
F
C
D
S
N
B
A
P
Управление докладчиком

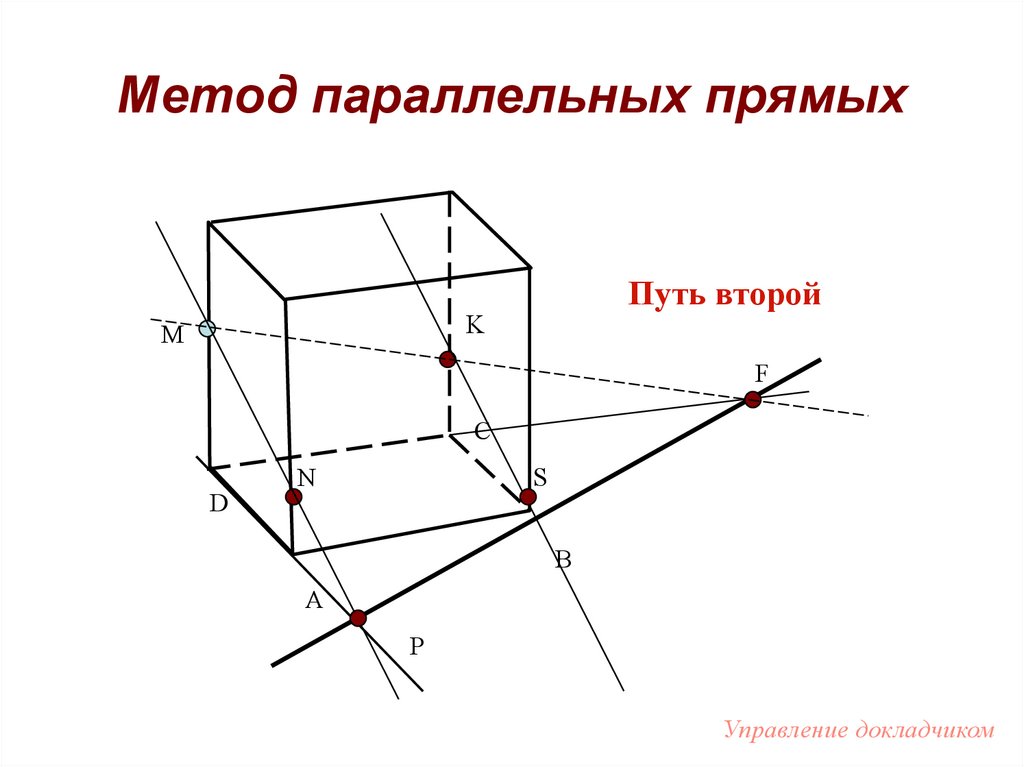
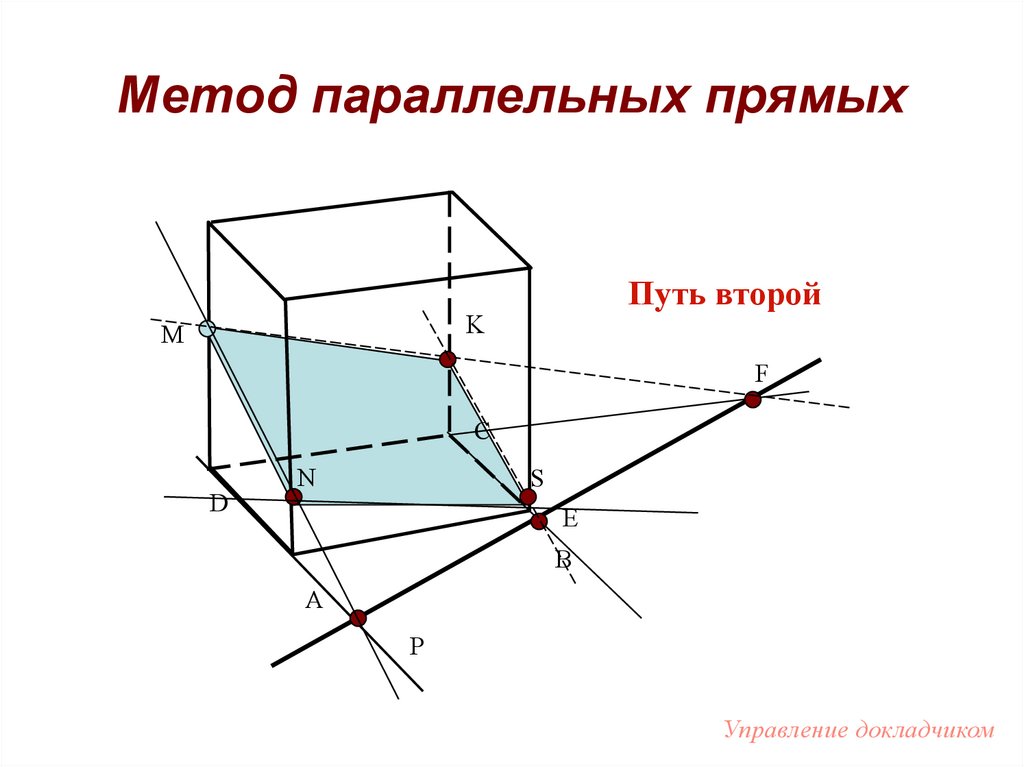
103.

Метод параллельных прямых
Путь второй
K
M
F
C
D
N
S
E
B
A
P
Управление докладчиком

104.

Метод параллельных прямых
Путь второй
K
M
F
C
D
N
S
E
B
A
P
Управление докладчиком

105. При подготовке работы были использованы

• «Построение сечений многогранников», составитель:
Екимова Ирина Викторовна, учитель информатики,
МОУ «СОШ №36» г.Норильска;
• «Построение сечений многогранников», составитель:
Мачихина Зинаида Ефимовна,ПЛ №17;
• «Построение сечений многогранников», Сейтова
Галина Евгеньевна, учитель информатики школы
№198, г. Москва;
• «Построение сечений многогранников», Остапенко
Ирина Евгеньевна, МОУ «Гимназия №6» (УВК
«Бекар»)