Похожие презентации:
Некоторые элементы теории множеств
1.
НЕКОТОРЫЕЭЛЕМЕНТЫ ТЕОРИИ
МНОЖЕСТВ
2.
ПОНЯТИЕ МНОЖЕСТВА- используют для описания совокупности некоторых
предметов или объектов, обладающих определенным
набором свойств.
Предметы одной совокупности могут отличаться др.
от др. и от предметов другой совокупности.
Элементы множеств - объекты этих множеств.
A, B, C, ... – множества
a, b, c, ... - элементы множеств
а А - a - элемент множества
A
а А - a не является элементом множества A
2
3.
5 R;-10 Z;
0,5 N
Виды множеств
Конечные - содержат определенное число элементов.
Бесконечные - содержат бесконечное число
элементов.
Пустое - не содержит ни одного элемента .
3
4.
СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ1. Перечисление элементов множества
M = {2, 3, 5, 7} или M = {7, 3, 2, 5}
2. Характеристическое свойство
A = {x: x p(x)}
Множество четных натуральных чисел, которые
больше 2, но меньше 20.
A = {x: x=2k, k N, 2 k 9}
4
5.
A и B - равны, если они состоят из одних и тех жеэлементов.
x A x B
A = B
A = {5, 6, 7}; B = {6, 7, 5} => A = B
B - подмножество A, если каждый элемент B
является элементом A.
b B => b A
B A (В включено в А)
A = {1, 2, 3, 4, 5, 6};
B = {2, 4, 6} => B A
5
6.
Если в B найдется хотя бы один элемент, непринадлежащий A, то B не будет являться
подмножеством A.
B A
[a, b] [a, b)
Свойства:
1.
2.
A A
A
6
7.
ЧИСЛОВЫЕ МНОЖЕСТВА- множества, элементами которых являются числа.
1, 2, 3, ..., n, ...
образуют множество натуральных
чисел
N = {1, 2, 3, ..., n, ...}
Множество целых чисел - натуральные числа, им
противоположные и 0.
Z = {0, 1, 2, ..., n, ...}
7
8.
Множество рациональных чисел - числа,представимые в виде несократимой дроби m/n, где
m Z, n N
Q={m/n, m Z, n N}
Иррациональные числа – числа, представимые в
виде бесконечной десятичной непериодической
дроби.
= 3,14...
2 = 1,41 ...
Рациональные и иррациональные числа образуют
множество действительных чисел (R).
N Z Q R
8
9.
ЧИСЛОВЫЕ ПРОМЕЖУТКИa, b R, a < b
1. [a, b]={x R: a<x<b} - числовой отрезок
x [a, b]
2. (a, b)={x R: a<x<b} - числовой интервал
x (a, b)
3. Бесконечные числовые интервалы:
(a; + )={x R: x>a},
( ; a)={x R: x<a},
( ;+ )={x R},
x (a, + )
x ( , a)
x ( , + )
9
10.
ОПЕРАЦИИ НАД МНОЖЕСТВАМИОбъединением (суммой) нескольких множеств
называется множество, содержащее те и только те
элементы, которые входят хотя бы в одно из данных
множеств.
А В = {х | х А или х В}
Пусть A и B непустые множества. Найти A B
А В=C
C
B
10
11.
CА В=C
B
A
A
А В=A
B
11
A A = A, A = A
для А
12.
a). Пусть A = [1; 3], B = [2; 4), найти A B.1
2
3
4
х
A B = [1; 4)
12
13.
b). Пусть A = ( 6; 8), B = [0; 3/2], найти A B.-6
0
3/2
8
х
A B = ( 6; 8)
с). Пусть A = ( 10; 5]; B = [3; 7). Найти A B .
-10
-5
3
A B = ( 10; 5] [3; 7)
7
х
13
14.
ПЕРЕСЕЧЕНИЕ МНОЖЕСТВПересечением (произведением) нескольких
множеств называется множество, содержащее те и
только те элементы, которые входят в каждое из
данных множеств.
C=A B
А В = {х | х А и х В}
Пусть A и B непустые множества. Найти A B
A
B
А В=
14
15.
CA
А В=C
B
A
А В=B
B
A A = A, A =
для А
15
16.
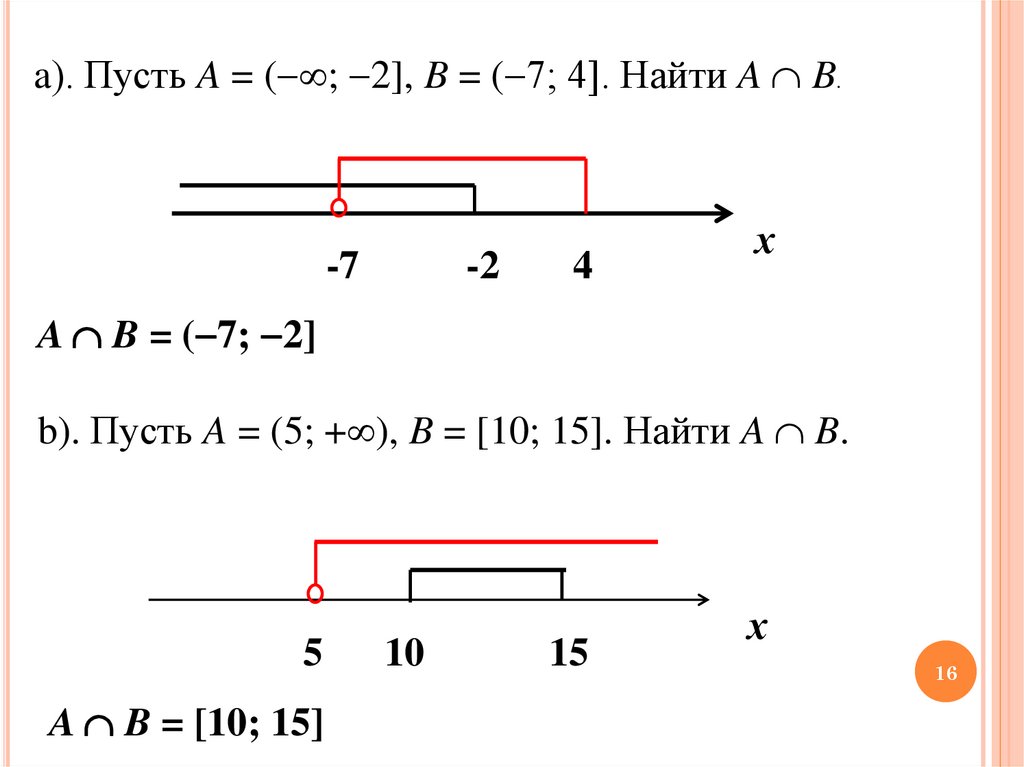
a). Пусть A = ( ; 2], B = ( 7; 4]. Найти A B.-7
-2
4
х
A B = ( 7; 2]
b). Пусть A = (5; + ), B = [10; 15]. Найти A B.
5
A B = [10; 15]
10
15
х
16
17.
c). Пусть A = (- ; 0), B = [1; + ). Найти A B.0
1
х
A B=
17
18.
АЛГЕБРАИЧЕСКИЕ СВОЙСТВАU - универсальное множество, т.е. все
рассматриваемые объекты, являются его элементами.
1. A (B C)=(A B) C
1'. A (B C)=(A B) C
2. A B=B A
2'. A B=B A
3.A (B C)=(A B) (A C 3'.A (B C)=(A B) (A C
)
)
4. A =A
4'. A U=A
ഥ =U
ഥ =
5. A А
5'. A А
18
19.
РАЗНОСТЬ МНОЖЕСТВРазностью множеств A и B называется множество
C, состоящее из тех и только тех элементов множества
A, которые не принадлежат множеству B.
С= A \ B
А \ В = {х | х А, х В}
Пусть A и B непустые множества. Найти A \ B
A
B
А \ В=A
19
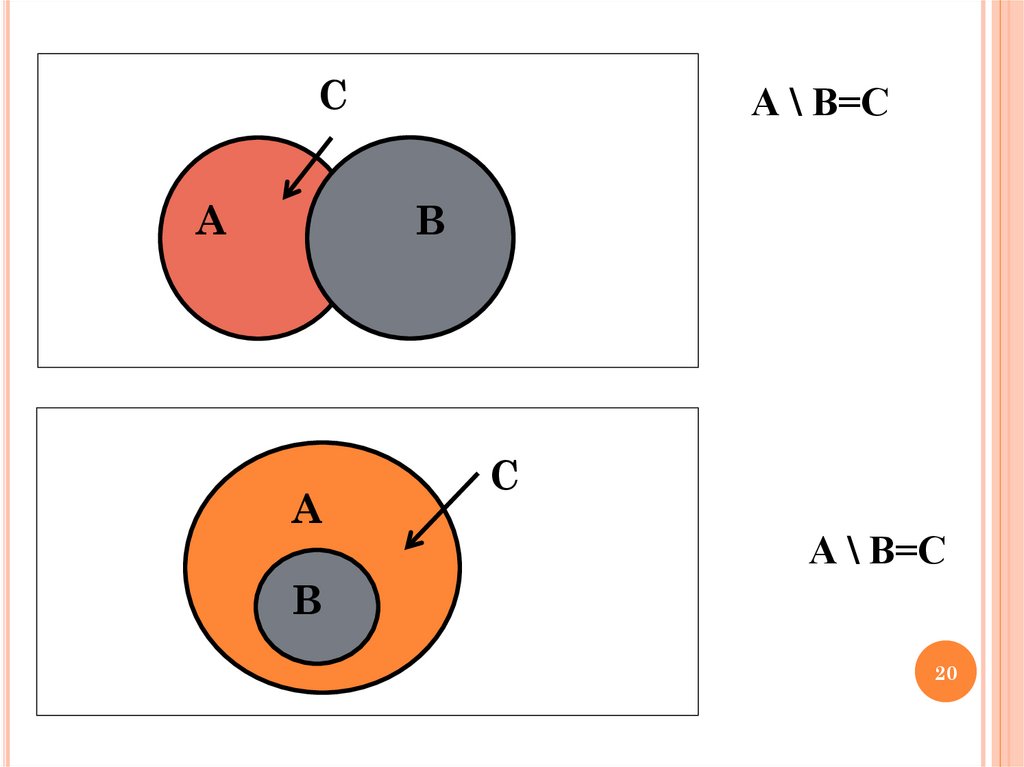
20.
CA
А \ В=C
B
A
C
А \ В=C
B
20
21.
a). Пусть A = ( ; 2], B = ( 7; 4]. Найти A \ B.A \ B = ( ; 7]
-2
-7
х
4
b). Пусть A = (5; + ), B = [10; 15]. Найти A \ B.
5
10
A \ B = (5; 10) (15; + )
15
х
21
22.
c). Пусть A = (- ; 0), B = [1; + ). Найти A \ B.0
1
х
A \ B = (- ; 0)
22
23.
Если множество B A, то разность A \ B называетсядополнением множества B до множества A.
ത или






















 Математика
Математика








