Похожие презентации:
Элементы теории множеств
1.
ЭЛЕМЕНТЫТЕОРИИ МНОЖЕСТВ
1
2.
1.1. СИСТЕМЫ МНОЖЕСТВНепустой класс множеств K называется кольцом, если
A, B K A B K и A \ B K .
Свойства колец
1 . Всякое кольцо содержит .
2 . Всякое кольцо замкнуто относительно операций и .
3 . Всякое кольцо замкнуто относительно конечных объединений и пересечений, т.е. если i Ai K , то
m
i 1
Ai K и
m
Ai K .
i 1
4 . Пересечение любого количества колец является кольцом.
5 . Для любого непустого класса M существует наименьшее кольцо K M ,
содержащее M . Это кольцо включает в себя те, и только те множества, которые либо входят в M , либо получаются из множеств класса M посредством
конечного числа операций , \ (а так же, в силу свойства 2, и ).
3.
Равенство вида AAn будем называть разложением множества A
n 1
на элементы класса S (конечным или бесконечным), если
n An S и i j Ai
Aj
Класс S называется полукольцом, если A, B S A
A \ B допускает конечное разложение A \ B
n
i 1
B S и разность
Ai , Ai S .
Свойства полуколец
1 . Всякое полукольцо содержит .
A \ A .
2 . Всякое полукольцо замкнуто относительно конечного пересечения.
3 . Всякое кольцо является полукольцом. Обратное утверждение,
в общем случае, неверно.
4 . Если S – полукольцо, то наименьшее кольцо K S , содержащее S ,
совпадает с системой множеств, допускающих конечное разложение на
элементы класса S .
5
4.
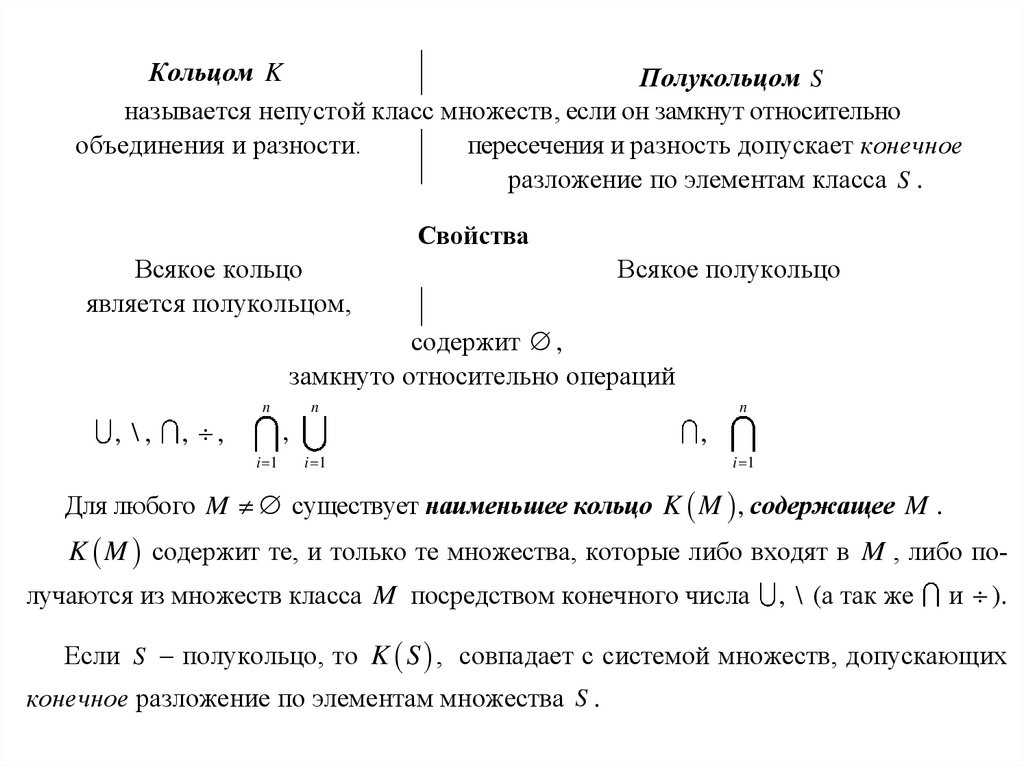
Кольцом KПолукольцом S
называется непустой класс множеств, если он замкнут относительно
объединения и разности.
пересечения и разность допускает конечное
разложение по элементам класса S .
Свойства
Всякое кольцо
является полукольцом,
Всякое полукольцо
содержит ,
замкнуто относительно операций
, \,
, ,
n
n
,
i 1
n
,
i 1
i 1
Для любого M существует наименьшее кольцо K M , содержащее M .
K M содержит те, и только те множества, которые либо входят в M , либо получаются из множеств класса M посредством конечного числа
, \ (а так же
и ).
Если S – полукольцо, то K S , совпадает с системой множеств, допускающих
конечное разложение по элементам множества S .
5.
Кольцо K называется -кольцом (борелевским кольцом), еслиAi K
Ai K .
i 1
Свойства -колец
1-4. Всякое -кольцо обладает всеми свойствами колец.
5. Всякое -кольцо замкнуто относительно счетного пересечения.
i 1
Ai A1 \
A1 \ An .
n 1
6. Пересечение любого количества -колец – -кольцо.
7. Для любого непустого класса M существует наименьшее борелевское
кольцо (борелевское замыкание класса M ), содержащее M . Это кольцо включает в себя те, и только те множества, которые либо входят в M , либо
получаются из элементов класса M посредством конечной или счетной совокупности операции , \ (а так же, в силу свойства 2, и ).
7
6.
Пусть M .Множество A0
A M
A называют единицей класса M , если A0 M .
Кольцо ( -кольцо) множеств с единицей называется алгеброй
( -алгеброй).
Свойства алгебры ( -алгебры)
1. Всякая алгебра ( -алгебра) является кольцом ( -кольцом),
а значит, обладает всеми свойствами колец ( -колец).
2. Если A0 – единица алгебры K , то A K A0 \ A K .
8
7.
Кольцо K называется -кольцом, если Ai KAi K .
i 1
Свойства -колец
1-4. Всякое -кольцо обладает всеми свойствами колец.
5а. Всякое -кольцо является -кольцом.
Следует из 5-го свойства -колец.
5б. Обратное в общем случае неверно.
Пусть K – класс всех ограниченных множеств пространства n . Класс
K является -кольцом, но не является -кольцом, так как счетное объединение
орграниченных множеств может быть неограниченным множеством.
5в. -кольцо с единицей является -кольцом с единицей, а значит, и
-аглеброй.
Пусть A0 единца кольца K . Если Ai K , то
i 1
Ai A0 \
A0 \ Ai K .
i 1
6. Пересечение любого количества -колец – -кольцо.
9
8.
Примеры:1 . Если A , то система A, – -алгебра с единицей A0 A .
2. Для любого множества A булеан (система всех его подмножеств) является
-алгеброй с единицей A0 A .
3. Система всех конечных (не более чем счетных) подмножеств произвольного фиксированного множества A является кольцом множеств. Это кольцо будет -алгеброй
тогда и только тогда, когда множество A само конечно (не более чем счетно).
4 . Пусть a, b . Тогда
– множество всех интервалов a, b , отрезков a, b , полуинтервалов a, b и a, b
на числовой прямой1 является полукольцом, но не является кольцом,
– множество всех интервалов a, b , отрезков a, b , полуинтервалов a, b и a, b
на числовой прямой и конечных систем таких полуинтервалов является кольцом,
– множество всех промежутков числовой оси и конечных систем таких промежутков является -алгеброй с единицей .
При этом в число интервалов включается «пустой» интервал a, a , а в число отрезков – отрезок,
10
состоящий из одной точки a , a .
1
9.
5 . Пусть a, b, c, d . Тогда– множество всех прямоугольников вида a, b c, d является полукольцом, но не является кольцом,
– множество всех прямоугольников вида a, b c, d и конечных систем
таких прямоугольников является кольцом.
6 . Система всех ограниченных множеств A
жеств, не содержащим единицы.
n
является кольцом мно-
7 . Система всех ограниченных подмножеств произвольного множества
A n является кольцом множеств. Это кольцо будет алгеброй тогда и
только тогда, когда множество A ограничено.
11
10.
1.2. КЛАССЫ МНОЖЕСТВ M И MПусть M – непустой класс множеств. Тогда M ( M ) – класс всевозможных счетных объединений (пересечений) множеств класса M . Множества
из класса M ( M ) будем называть -множествами ( -множествами).
Свойства классов M и M
1. Класс M ( M содержит все конечные объединения (пересечения)
множеств из M , в частности M M , M M .
2. Конечное или счетное
– объединение -множеств есть -множество,
– пересечение -множеств есть -множество.
3. Если M – кольцо, то конечное
– пересечение -множеств есть -множество,
– объединение -множеств есть -множество.
З а м е ч а н и е . Cчетное
– пересечение -множеств может не быть -множеством,
– объединение -множеств может не быть -множеством.
А значит, -множество может не быть -множеством и наоборот.
12
11.
4. Если M1 M 2 , то M1 M 2 , M1 M 2 .5. Если M – кольцо, Q M , P M , то Q \ P M , P \ Q M .
6. Пусть M – кольцо. Тогда
а) Всякое Q M можно представить в виде счетного разложения
Q
An , An M .
n 1
б) Всякое Q M можно представить в виде Q
A1 A2 ... An ... .
в) Всякое P M можно представить в виде P
A1 A2 ... An ... .
An , An M , где
n 1
An , An M , где
n 1
7. Если H – полукольцо, а M K H – кольцо, минимальное над H , то M H .
8. Если M – борелевское кольцо, то M M M .
9. Если M M , то M – борелевское кольцо (и притом минимальное над M ).
14
12.
ПустьF – класс замкнутых множеств пространства
n
,
B= (F ) – борелевское замыкание класса F .
Множество n замкнуто и является единицей класса F , следовательно, B – борелевская алгебра.
Множества, входящие в класс B, называются борелевскими множествами или B–множествами.
Можно доказать, что класс B одновременно является борелевским
замыканием класса G всех открытых множеств пространства n .
Следовательно, все множества, полученные из открытых и замкнутых множеств пространства n с помощью конечного или счетного
числа операций , , \ , являются B–множествами.
15
13.
Примеры борелевских множеств0,1 ,
A a, ,
а) A
б)
\
1
1
в) A n n , n n ,
3
2
n 1
г) A 0,3 1, 2 \
д) A
,
2
x
,
y
x
,
y
,0
y
x
, 1 x 2 ,
16
14.
1.3. ФУНКЦИИ МНОЖЕСТВАГоворят, что на классе K задана функция множества , если
для каждого множества A K определено число A
, .
Функция называется:
– неотрицательной, если A K A 0 ;
– монотонной, если A B , то A B ;
– аддитивной, если A, B K из того, что A
A, B K
B , следует
A B A B A B ;
– счетно-аддитивной (или -аддитивной), если Ai K из того,
что Ai
Aj при i j , следует
Ai Ai .
i 1 i 1
17
15.
Теорема 1.1. Всякая аддитивная функция , заданная на полукольце(в частности, кольце) K , обладает свойствами:
– конечной аддитивности – если A1 , A2 ,..., An попарно непересекаю-
n n
щиеся множества кольца, то Ai Ai .
i 1 i 1
– субтрактивности – A, B K если A B и B , то
B \ A B A .
Следствия: 1. 0 .
2. A, B K A B A B A B ,
3. A, B K B \ A B A A \ B .
Теорема 1.2. Всякая неотрицательная аддитивная функция ,
заданная на полукольце (в частности, кольце) K , является монотонной.
18
16.
Теорема 1.3. Пусть неотрицательная аддитивная функциязаданна на кольце K и A, A1 , A2 ,..., An K . Тогда
n
1) если A1 , A2 ,..., An попарно не пересекаются и
Ai A , то
i 1
n
A A ;
i
i 1
2) если A
n
i 1
n
Ai , то A Ai .
i 1
Следствие. В случае -кольца первое утверждение будет
справедливо и для n . Второе утверждение будет справедливо при n тогда и только тогда, когда функция является
неотрицательной и -аддитивной.
20
17.
Теорема 1.4 (непрерывность счетно-аддитивной функции, заданной на кольце). Пусть – счетно-аддитивная функция, определеннаяна кольце K , A, A1 , A2 ,..., An ,... K . Тогда,
1) если A1 A2 ... An ... и A
2) если A1 A2 ... An ... и A
i 1
i 1
Ai , то lim An A ;
n
Ai , то lim An A .
n
Следствие.
1) Если i Ai K и A
2) Если i Ai K и A
i 1
i 1
n
Ai K , то lim Ai A .
n
i 1
n
Ai K , то lim Ai A .
n
i 1
23
















 Математика
Математика








