Механика материалов. Лекция 6. Теории прочности и разрушения

1.

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА
кафедра «Локомотивы»
МЕХАНИКА МАТЕРИАЛОВ
Лектор: к.т.н., доцент Комиссаров Виктор Владимирович
п.з.: ассистент Таранова Елена Сергеевна
Форма контроля знаний – экзамен
(по всем вопросам обращаться на кафедру ауд. 1410)
ГОМЕЛЬ, 2022

2.

Лекция 6
ТЕОРИИ ПРОЧНОСТИ
И РАЗРУШЕНИЯ

3.

23.1 Прочность при сложном
напряженном состоянии
3
Материал подавляющего большинства машин, механизмов и
приборов, созданных человеком, работает в пределах упругости,
ибо появление в нём необратимых (пластических) деформаций
или трещин приводит к поломке машины.
Предельным называют состояние напряжённого материала,
непосредственно
предшествующее
появлению
в
нём
пластических деформаций (у пластических материалов) или
трещин (у хрупких материалов).
Число n называется коэффициентом запаса прочности в точке
тела, если пропорциональное увеличение в n раз всех
компонент напряжённого состояния в этой точке приводит к
возникновению предельного состояния в её окрестности:

4.

23.1 Прочность при сложном
напряженном состоянии
4
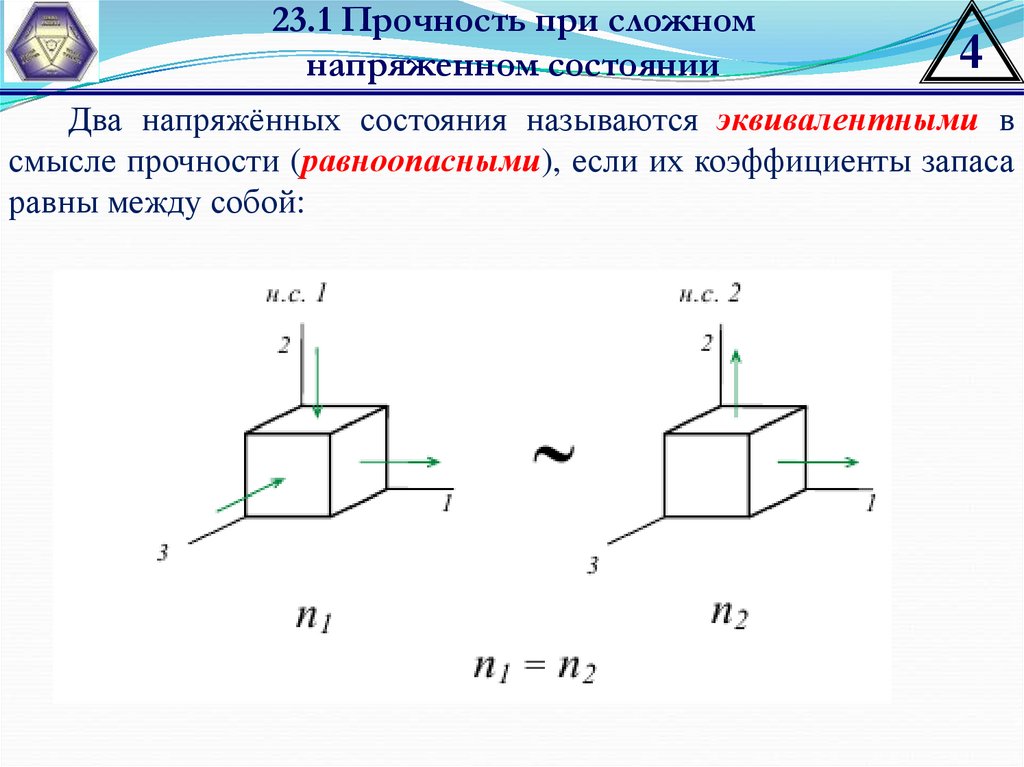
Два напряжённых состояния называются эквивалентными в
смысле прочности (равноопасными), если их коэффициенты запаса
равны между собой:

5.

23.1 Прочность при сложном напряженном
состоянии
5
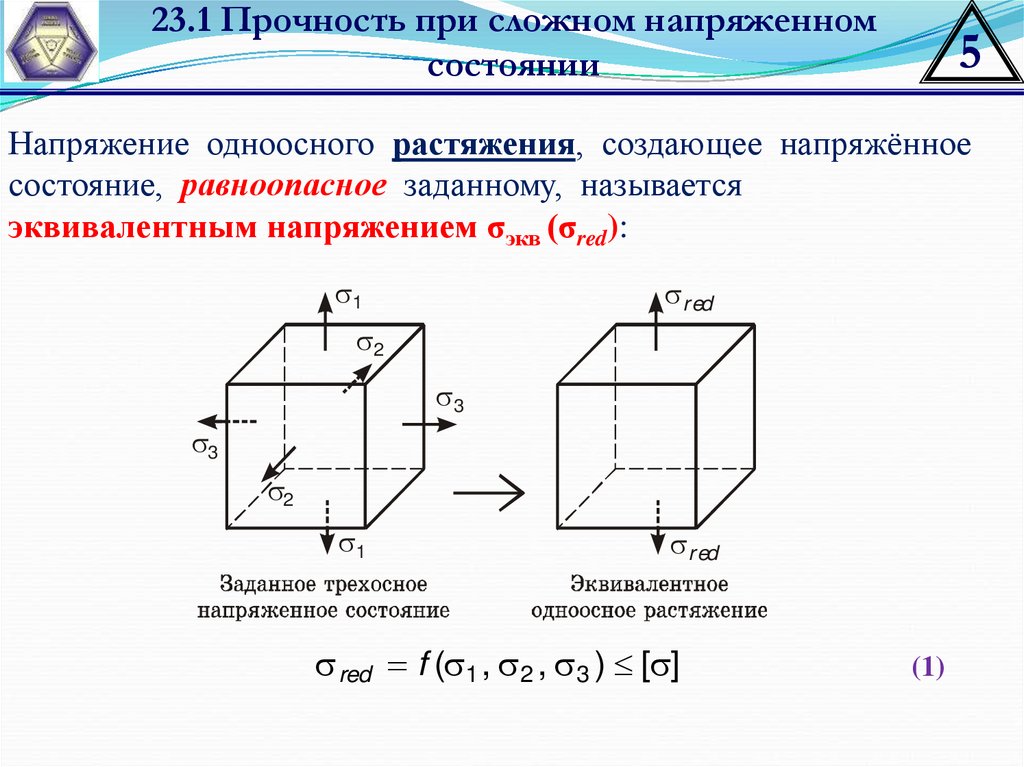
Напряжение одноосного растяжения, создающее напряжённое
состояние, равноопасное заданному, называется
эквивалентным напряжением σэкв (σred):
1
red
2
3
3
2
1
red
red f ( 1 , 2 , 3 ) [ ]
(1)

6.

23.1 Прочность при сложном напряженном
состоянии
6
При известном эквивалентном напряжении σэкв коэффициент
запаса прочности для данного напряжённого состояния
вычисляется по простой формуле:
yр
uр
(2)
n
;
n
экв
экв
Механизмы деформирования различных материалов также могут различаться.
Поэтому и теорий прочности существует несколько. Теории, в которых за
предельным состоянием предполагается начало пластических деформаций,
называются теориями текучести, а теории, в которых за предельным
состоянием
предполагается
начало
трещинообразования, называются
теориями разрушения.
Существует два подхода к построению теорий прочности:
1. Выдвигается гипотеза о преимущественном влиянии того или иного фактора
на процесс перехода материала в предельное состояние, которая в дальнейшем
проверяется экспериментами;
2. Теория строится на основе экспериментальных данных так, чтобы она не
только могла охватить все случаи, но и находилась в лучшем соответствии с
этими данными.

7.

23.2 Теория максимальных нормальных
напряжений (первая теория прочности)
7
Эта теория использует следующий критерий эквивалентности: два
напряженных состояния равноопасны, если у них равны наибольшие
нормальные напряжения.
Эквивалентное напряжение принимается равным максимальному по абсолютной
величине главному напряжению:
red max max 1 , 3
Условие прочности по первой теории записывается в виде
I
red
max 1 , 3 [ ]
(2)
Недостаток этой теории в том, что она учитывает только наибольшее из
главных напряжений, а влияние двух остальных игнорирует.
1
1
2
2

8.

;
23.3 Теория максимальных линейных
деформаций (вторая теория прочности)
8
Эта теория связывает переход в предельное состояние с моментом, когда
наибольшая деформация достигает определенного предельного значения,
которое устанавливается из опытов на растяжение (сжатие). Поэтому в ней
формулируется следующий критерий эквивалентности: два напряженных
состояния равноопасны, если у них равны наибольшие относительные
деформации.
Для сложного напряженного состояния с главными напряжениями 1, 2, 3,
когда 1 > | 3| (преимущественное растяжение), наибольшая деформация
определяется формулой
1 1 1 2 3
E
Для эквивалентного состояния одноосного растяжения
red red / E
Условие прочности по второй теории записывается в виде
IIred 1 2 3 [ ]
При преимущественном сжатии, т. е. когда | 3| > 1, условие прочности
принимает вид
II [ ]
red
3
1
(3)
2
Вторая теория прочности так же, как и первая, слабо соответствует
экспериментальным данным. Она удовлетворительно совпадает с экспериментом
лишь при разрушении хрупких материалов в сложных напряженных состояниях.

9.

;
23.4 Теория максимальных касательных напряжений
Треска – Сен-Венана (третья теория прочности)
9
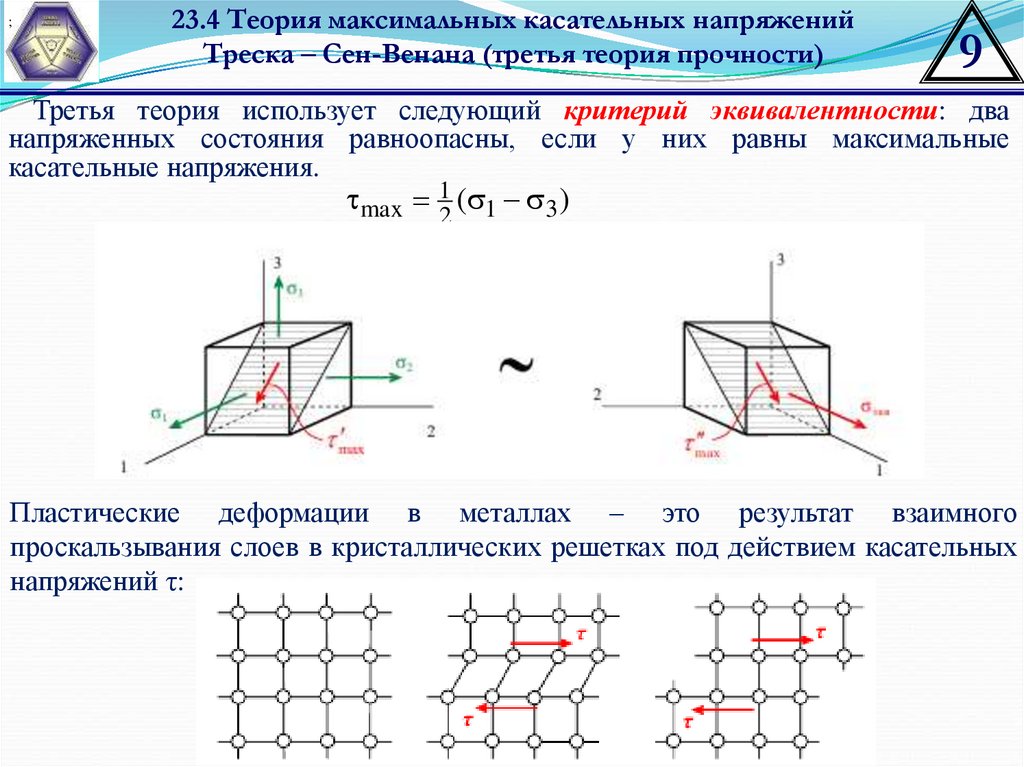
Третья теория использует следующий критерий эквивалентности: два
напряженных состояния равноопасны, если у них равны максимальные
касательные напряжения.
max 12 ( 1 3 )
Пластические деформации в металлах – это результат взаимного
проскальзывания слоев в кристаллических решетках под действием касательных
напряжений τ:

10.

;
23.4 Теория максимальных касательных напряжений
Треска – Сен-Венана (третья теория прочности)
10
Для эквивалентного одноосного растяжения напряжением σred максимальные
касательные напряжения
max red 12 red
Условие прочности по третьей теории записывается в виде
III
red
1 3 [ ]
(4)
Для большинства пластичных материалов пределы текучести при растяжении и
сжатии одинаковы, поэтому для них третья теория прочности достаточно
надежно предсказывает наступление текучести.
Третья теория прочности дает также удовлетворительные результаты и для
описания разрушения хрупких материалов в тех случаях, когда разрушение путем
отрыва невозможно, и оно происходит за счет сдвига по плоскостям действия
max. Так разрушаются хрупкие образцы при сжатии.
Таким образом, третья теория прочности позволяет рассматривать
предельные состояния текучести и хрупкого сдвига с единой точки зрения.

11.

;
23.4 Теория максимальных касательных напряжений
Треска – Сен-Венана (третья теория прочности)
11
Следствие. Сформулируем третью теорию прочности для брусьев, в опасных
точках которых одновременно возникают нормальные и касательные
напряжения (при изгибе с кручением, поперечном изгибе). В этом случае главные
напряжения
1 1 2 4 2 , 3 1 2 4 2 ,
2 2
2 2
следовательно, эквивалентное напряжение растяжения
red = 1 2 4 2 – 1 2 4 2 =
2 2
2 2
2 4 2 .
Поэтому выражение (4) принимает вид
2
2
III
4
[ ]
red
Впервые роль касательных напряжений при разрушении отметил Ш. Кулон
(1776). Связь пластического течения материалов с максимальными касательными
напряжениями была экспериментально установлена французским инженером
Треска). На основе его исследований Б. Сен-Венан сформулировал условие (8.3)
как условие пластичности и построил основные уравнения теории пластичности,
поэтому третью теорию прочности называют теорией Треска–Сен-Венана.

12.

;
23.5 Энергетическая теория Хубера– Мизеса–
Хенки (четвертая теория прочности)
12
Энергетический критерий эквивалентности: два напряженных состояния
равноопасны, если у них равны потенциальные энергии изменения формы.
Именно эта часть удельной потенциальной энергии участвует в разрушении
материала. В общем случае напряжённого состояния:
В сложном напряженном состоянии энергия формоизменения в главных
напряжениях определяется вторым из соотношений
U d 1 ( 1 2 )2 ( 2 3 )2 ( 3 1 )2
6E
По той же формуле для простого растяжения с эквивалентным напряжением
1 = red получаем
1 2
U d red
6E
2 red

13.

;
23.5 Энергетическая теория Хубера– Мизеса–
Хенки (четвертая теория прочности)
13
Условие прочности по четвертой теории
IV
red
2 ( )2 ( )2 ( )2 [ ]
1
2
2
3
3
1
2
(5)
Достоинством четвертой теории является то, что учитываются все три главных
напряжения и не требуется в процессе расчета следить за их нумерацией, так как
в соотношение (5) они входят равноправно. Это позволяет отказаться от строгой
их расстановки в порядке убывания и связать с направлениями координатных
осей.
Следствие. При изгибе с кручением и поперечном изгибе эквивалентное
напряжение
red
2 2 2 ( )2 = 2 2 2 6 2 =
1
3
3
1
2
2
2 3 2 .
Условие прочности по четвертой теории принимает вид
2
2
IV
3
[ ]
red
Полученная формула дает меньшее значение red для изгиба с кручением, чем
третья теория прочности.

14.

;
23.6 Теория предельных состояний Мора
(пятая теория прочности)
14
Рассмотренные ранее теории прочности применимы для расчёта весьма
пластичных материалов, имеющих равные по модулю пределы текучести при
растяжении σyt и при сжатии σyc.
При расчётах конструкций из умеренно пластичных (σyt < [σyt]) и хрупких
(σut < [σut], а σy нет вообще) материалов пользуются формулой теории
прочности Мора.
Условие прочности выглядит следующим образом:
V
red
1 k 3 [ ]
(6)
где k – коэффициент, численно равный отношению предельных напряжений при
линейном растяжении и сжатии;
k lim t lim c
Для пластичных материалов эти напряжения одинаковы, следовательно,
k = 1, и условие (6) формально совпадает с теорией Треска–Сен-Венана (4).
Наилучшие результаты теория Мора дает для смешанных напряженных
состояний, т. е. при σ1 > 0 и σ3 < 0.

15.

;
23.6 Теория предельных состояний Мора
(пятая теория прочности)
15
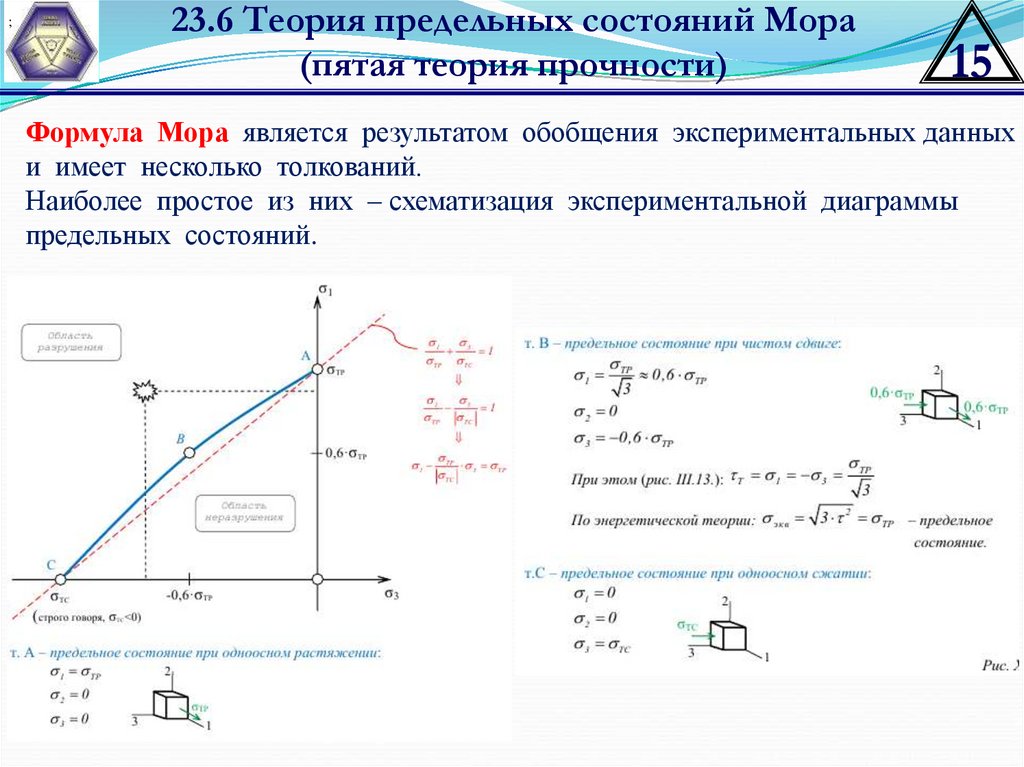
Формула Мора является результатом обобщения экспериментальных данных
и имеет несколько толкований.
Наиболее простое из них – схематизация экспериментальной диаграммы
предельных состояний.

16.

;
23.7 Заключение
16
В заключении хотелось бы заметить: расчёты по всем, существующим на
данный момент теориям прочности, дают удовлетворительные результаты только
в том случае, когда в напряжённом состоянии доминирует девиатор, то есть
экстремальные главные напряжения σ1 и σ3 имеют разные знаки, либо одно из
них равно нулю.
В случае, когда все главные напряжения одного знака в напряжённом
состоянии доминирует шаровой тензор и на результаты расчётов σэкв по
формулам теорий прочности полагаться нельзя, необходимо проводить
экспериментальные исследования.
* Схема а) пусть не вводит в заблуждение схожестью с предыдущими
рисунками, просто, когда значения главных напряжений неизвестны, их
принято изображать в положительном направлении.