Технические теории прочности

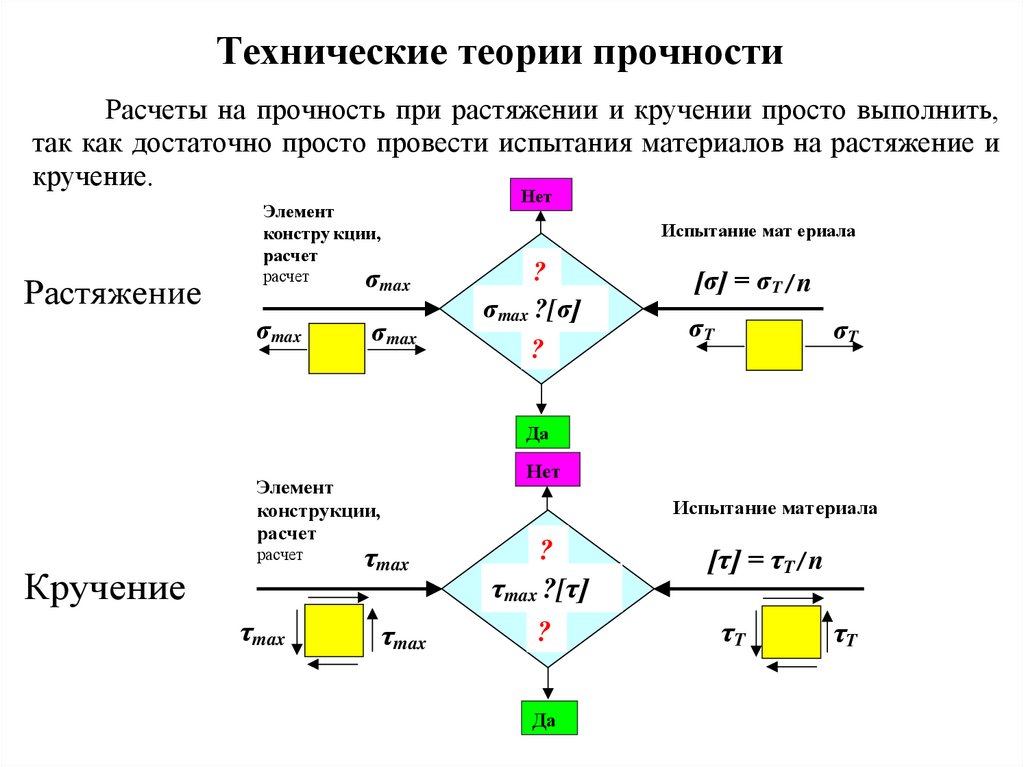
1. Технические теории прочности

Расчеты на прочность при растяжении и кручении просто выполнить,
так как достаточно просто провести испытания материалов на растяжение и
кручение.
Нет
Элемент
констру кции,
расчет
Растяжение
Испытание мат ериала
расчет
σmax
σmax
σmax
?
σmax ?[σ]
?
[σ] = σ T / n
σT
σT
Да
Нет
Элемент
конструкции,
расчет
расчет
Кручение
τmax
Испытание материала
τmax
?
τmax ?[τ]
τmax
?
Да
[τ] = τT / n
τT
τT

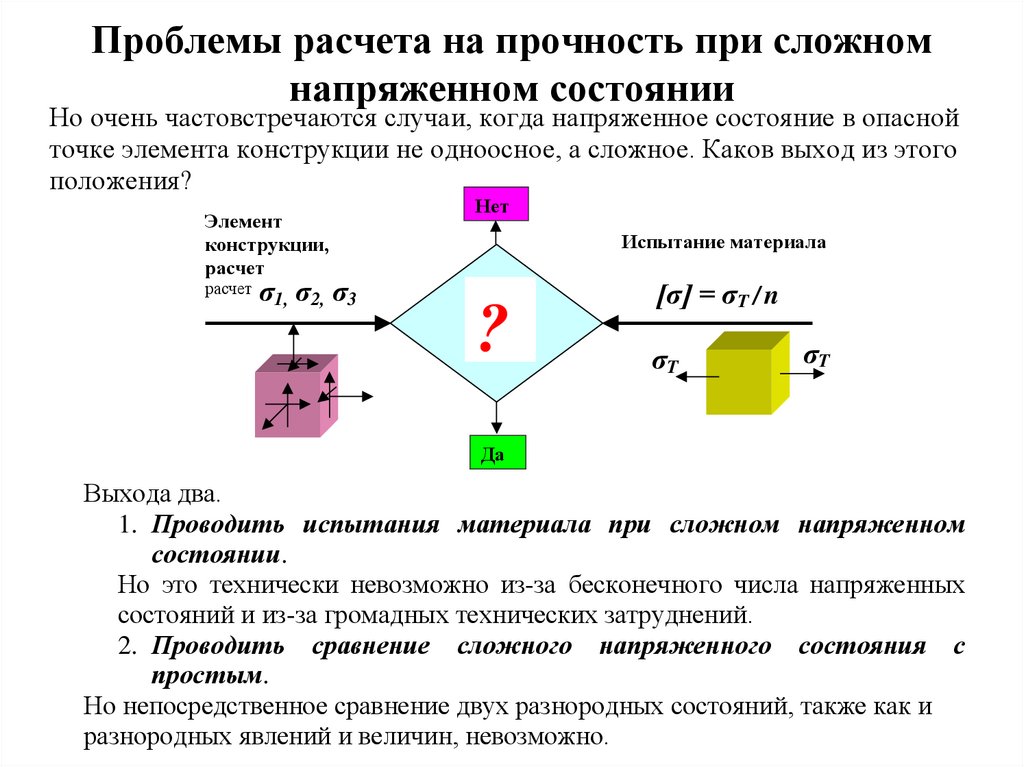
2. Проблемы расчета на прочность при сложном напряженном состоянии

Но очень частовстречаются случаи, когда напряженное состояние в опасной
точке элемента конструкции не одноосное, а сложное. Каков выход из этого
положения?
Элемент
конструкции,
расчет
расчет
σ1, σ2, σ3
Нет
Испытание материала
?
[σ] = σT / n
σT
σT
Да
Выхода два.
1. Проводить испытания материала при сложном напряженном
состоянии.
Но это технически невозможно из-за бесконечного числа напряженных
состояний и из-за громадных технических затруднений.
2. Проводить сравнение сложного напряженного состояния с
простым.
Но непосредственное сравнение двух разнородных состояний, также как и
разнородных явлений и величин, невозможно.

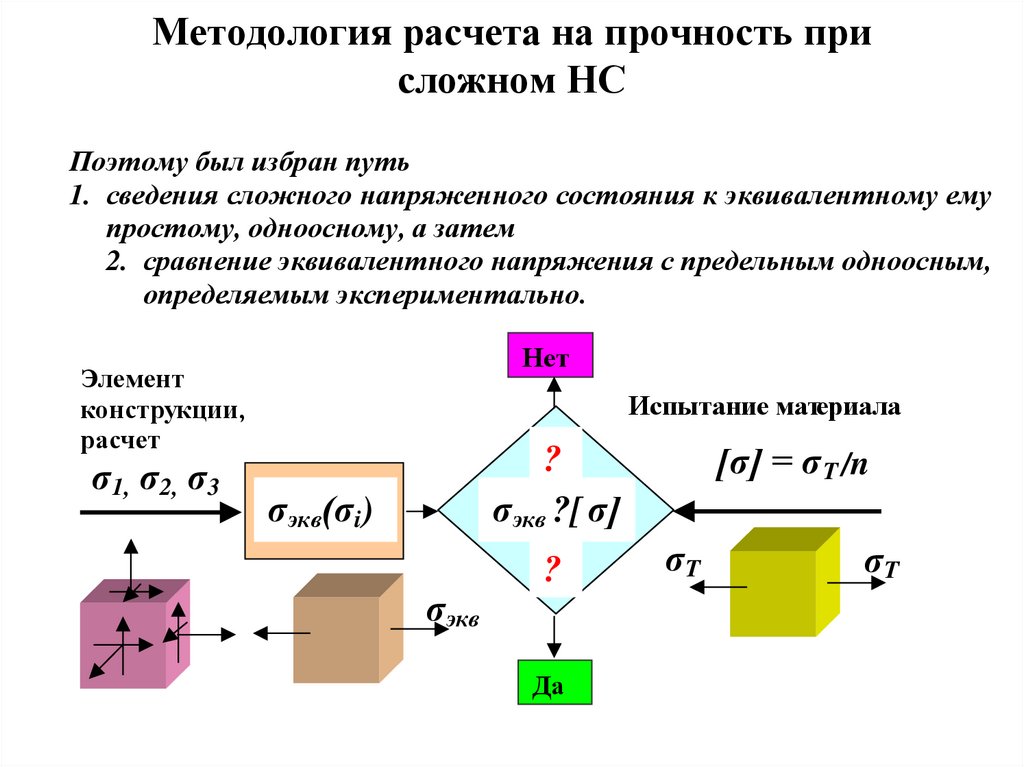
3. Методология расчета на прочность при сложном НС

Поэтому был избран путь
1. сведения сложного напряженного состояния к эквивалентному ему
простому, одноосному, а затем
2. сравнение эквивалентного напряжения с предельным одноосным,
определяемым экспериментально.
Нет
Элемент
конструкции,
расчет
σ1, σ2, σ3
Испытание материала
[σ] = σ T /n
?
σэкв ?[ σ]
σэкв(σi)
σэкв
?
Да
σT
σT

4. Предельные состояния материала

1. Упругое состояние. В этом состоянии материал содержит
определенную упругую потенциальную энергию. Но этой энергии еще
недостаточно, чтобы могли идти необратимые процессы пластического
деформирования или роста трещин.
2. Упругопластическое состояние. В этом состоянии избыток упругой
энергии тратится на необратимые пластические деформации.
3. Состояние хрупкого разрушения. В этом состоянии упругой энергии
достаточно, чтобы поддерживать неконтролируемый рост трещин.
Предельным напряженным состоянием называют такое напряженное
состояние, при котором происходит качественное изменение поведения
материала, переход от одного механического состояния к другому.
Для пластичных материалов за предельное напряженное состояние
принимают состояние, при котором появляются первые необратимые
пластические деформации.
Для хрупких материалов предельное напряженное состояние
ассоциируют с состоянием, при котором появляются трещины.

5. Эквивалентное напряжение

Два напряженных состояния эквивалентны,
если они равноопасны.
σ2
σэкв
σ1
σ3
1
2
Состояния 1 и 2 равноопасны. Поэтому
состояние 2 эквивалентно сoстоянию 1
Эквивалентным напряжением
σэкв будем называть такое
напряжение, которое нужно создать в растянутом образце, чтобы
возникающее в нем одноосное напряженное состояние стало равноопасным
с заданным двухосным или трехосным напряженным состоянием.

6. Миссия теорий прочности

Но нам необходим критерий эквивалентности, который поможет нам
вычислять эквивалентное напряжение
экв f 1 , 2 , 3 ,
как функцию
состояния.
главных
компонент
рассматриваемого
напряженного
Эту задачу выполняют теории прочности.
В основе теорий прочности лежат гипотезы о преимущественном
влиянии на прочность одного или нескольких компонентов напряженного
состояния.
Эти гипотезы, но доведенные до соответствующего аналитического
выражения, позволяющего рассчитывать
прочности.
σэкв , называются теориями

7. Теория наибольших растягивающих напряжений (I теория)

Два напряженных состояния равноопасны, если равны наибольшие
нормальные напряжения, т.е.
экв 1 .
(1)
Критерий прочности имеет вид
эквI 1 p ,
где
р - допускаемое напряжение при растяжении
При одноосном сжатии
I*
σ3<0. В этом случае экв 3 ,
I*
и необходимо соблюдение критерия
экв 3 с ,
где
c - допускаемое напряжение при сжатии.

8. Теория наибольших линейных удлинений (II теория)

Два напряженных состояния будут равноопасны,
наибольшие относительные удлинения будут равны.
1
Для трехосного состояния : max 1 2 3
E
экв экв
Для одноосного напряженного состояния: max
E
.
С учетом равенства
экв
max
max
получаем
эквII 1 2 3
Критерий прочности:
эквII p .
Если σ3<0 , то необходимо соблюдение условия
эквII* 3 1 2 c
(2)
если

9. Теория наибольших касательных напряжений (III теория)

Два напряженных состояния будут равноопасны, если у них
равны наибольшие касательные напряжения.
max
Для трехосного напряженного состояния:
1 3
2
экв экв
max
Для одноосного напряженного состояния:
2
.
С учетом равенства
экв
max max получаем
экв III 1 3 .
Критерий прочности:
эквIII p
(3)

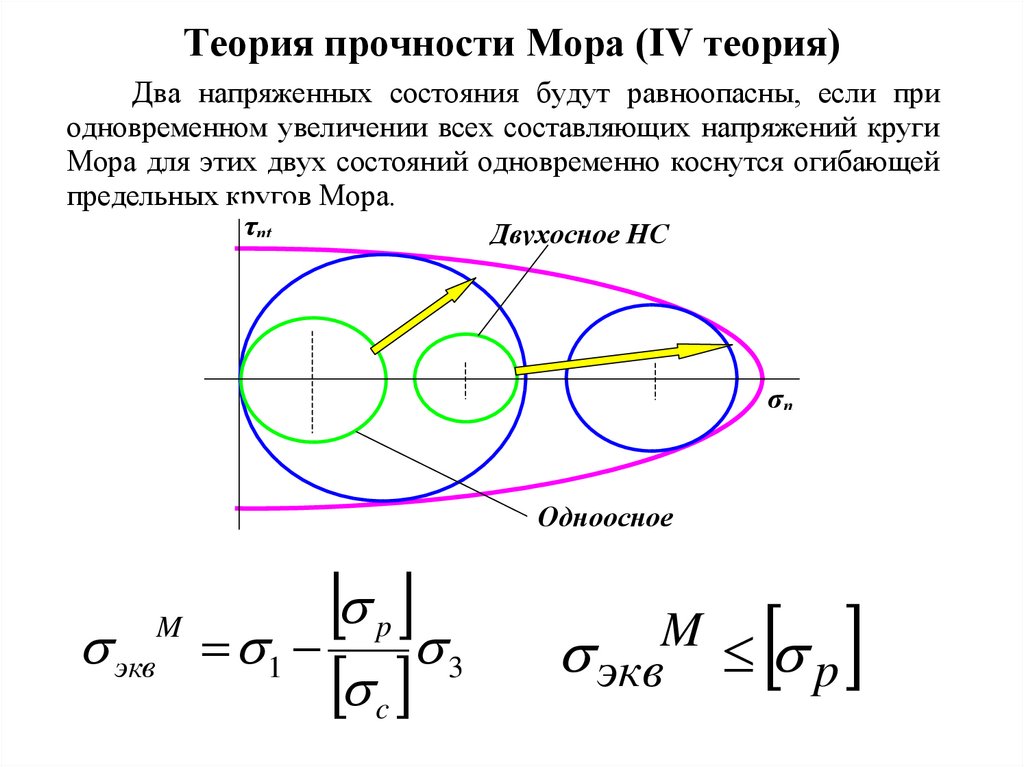
10. Теория прочности Мора (IV теория)

Два напряженных состояния будут равноопасны, если при
одновременном увеличении всех составляющих напряжений круги
Мора для этих двух состояний одновременно коснутся огибающей
предельных кругов Мора.
τnt
Двухосное НС
σn
экв
M
Одноосное
НС
p
1
c
3
M
экв p

11. Энергетическая теория прочности (V теория)

Два напряженных состояния будут равноопасны, если имеет место
равенство удельных потенциальных энергий формоизменения.
Для трехосного напряженного состояния:
1
1 2 2 2 3 2 1 3 2 .
aф
6E
экв 1 2
a
ф
экв
Для одноосного напряженного состояния:
3E
С учетом равенства
1
V
экв
2
экв
aф aф
получаем
1 2 2 2 3 2 1 3 2 (5)
V
Критерий прочности: экв p

12. Ограничения теорий прочности

Основные ограничения первой теории:
1. Теория не учитывает двух других главных напряжений σ2 и σ3;
2. Теория не учитывает возможность деформации сдвига.
Основное ограничение второй теории:
Теория основана на применении закона Гука для упругого состояния.
Но при достижении предельного состояния пластичности этот закон теряет
силу.
Основные ограничения третьей теории:
1. Теория не работает, если
растяжении.
1 3 , что имеет место при трехосном
2. Теорией предполагается, что
p с
.
3. Не учитывается среднее главное напряжение σ2.
Ограничение теории прочности Мора
Не учитывается среднее главное напряжение σ2.
Ограничения V теории прочности те же, что и для Ш теории.

13. Области применений теорий прочности

Для определения применимости той или иной теории прочности
необходима информация о механических свойствах данного
конструкционного материала.
1. Если материал хрупкий, то применяют I или II теорию
прочности;
2. Если материал пластичный, то применяют III или V теорию
прочности;
3. Если материал по разному сопротивляется растяжению и
сжатию, то применяют теорию прочности Мора (IV теория).

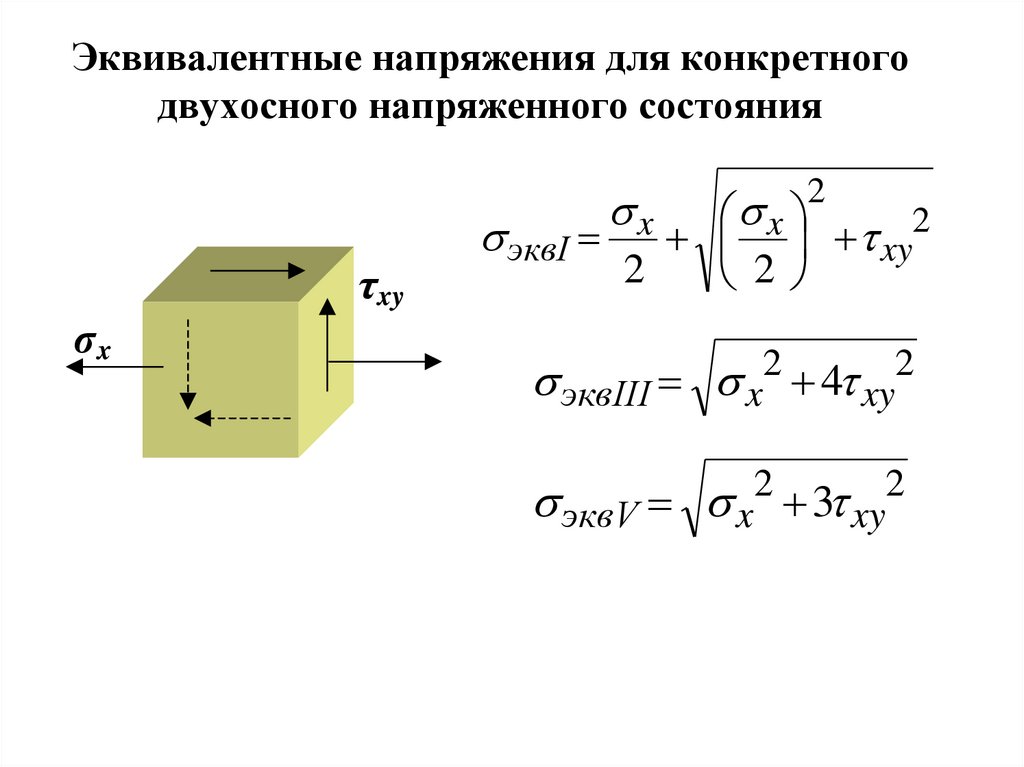
14. Эквивалентные напряжения для конкретного двухосного напряженного состояния

x
τxy
σx
2
x
2
эквI xy
2
2
эквIII x2 4 xy2
эквV x2 3 xy2

15. Эквивалентные напряжения для трехосного напряженного состояния (пример расчета)

622
Дан вектор главных напряжений
208
MPa
230
Даны механические свойства конструкционного материала
5
Модуль упругости
E
2 10
Коэффициент Пуассона
0.25
Допускаемое напряжение при растяжении
limP
400 MPa
Допускаемое напряжение при сжатии
limC
500 MPa
MPa

16. Эквивалентные напряжения для трехосного напряженного состояния (продолжение 1)

По пе рвой те ории прочности
eqvI
1
eqvI 622
MPa
По второй те ории прочности
eqvII
2
1
3
eqvII
627.5
MPa
eqvIII
852
MPa
eqvIV
806
MPa
eqvV
737.951
По третье й теории прочности
eqvIII
1
3
По че твертой теории прочности (Мор)
eqvIV
1
limP
limC
3
По пятой теории прочности
eqvV
1
2
1
2
2
2
3
2
1
3
2
MPa

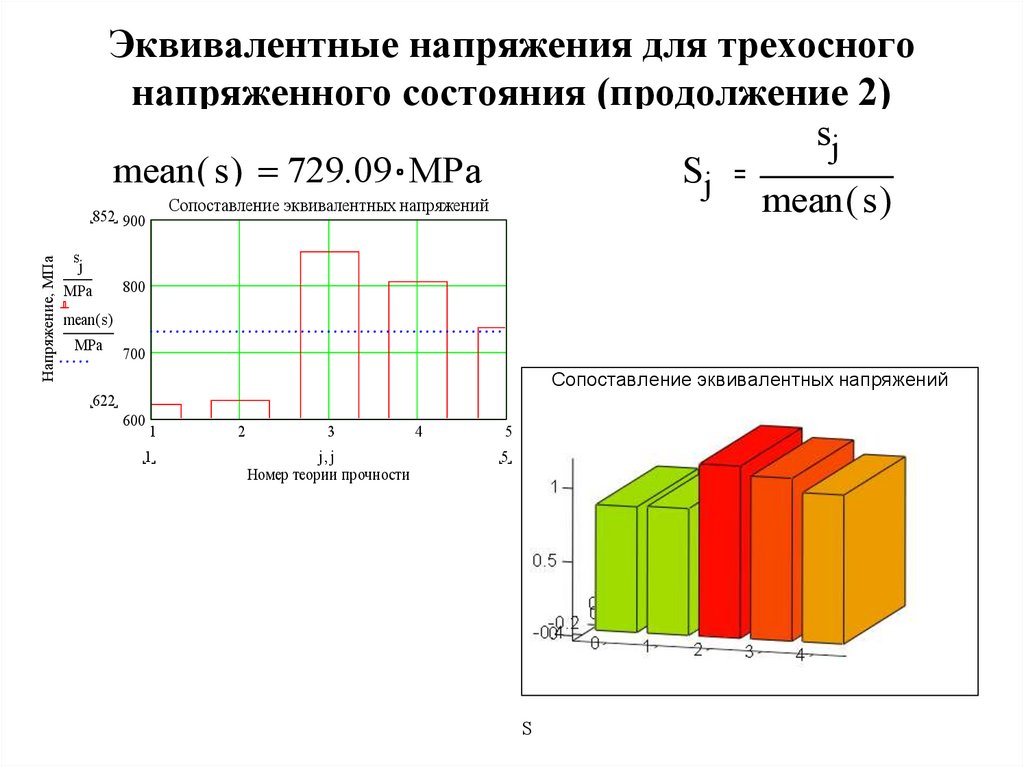
17. Эквивалентные напряжения для трехосного напряженного состояния (продолжение 2)

mean ( s ) 729.09 MPa
Сопоставление эквивалентных напряжений
852 900
Напряжение, МПа
Sj
sj
mean ( s )
s
j
MPa
800
mean( s )
MPa
700
Сопоставление эквивалентных напряжений
622
600
1
1
2
3
j j
Номер теории прочности
4
5
5
S