Похожие презентации:
Сложное движение точки
1.
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИПусть точка М движется относительно системы отсчета OXYZ ,
которая в свою очередь, движется относительно неподвижной
системы отсчета O1 X 1Y1Z1 . Такое движение точки М называется
составным или сложным.
Движение точки М относительно неподвижной системы
отсчета O1 X 1Y1Z1называется
абсолютным, а траектория,
.
скорость и ускорение точки М в этом движении – абсолютными.
z1
y
M
z
Обозначения:
(Vабс , aабс ) или (V , a ) .
O
O1
Движение точки М относительно подвижной системы
отсчета OXYZ называется относительным, а траектория,
1
скорость и ускорение точки М в этом движении – относительными.
x
x
y1
Обозначения: (Vотн , aотн ) или (Vr , ar ) .
Движение точки М вместе с подвижной системой отсчета OXYZ относительно
неподвижной системы отсчета O1 X 1Y1Z1 .называется переносным, а скорость и
ускорение той точки подвижной системы отсчета OXYZ , с которой совпадает
движущаяся точка М в данный момент времени – переносными.
Обозначения: (Vпер , aпер ) или (Ve , ae ) .
Основной задачей кинематики сложного движения точки является установление
зависимостей между скоростями и ускорениями абсолютного, относительного и
переносного движений.
1
2.
АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ ПРОИЗВОДНЫЕ ВЕКТОРАz1
Пусть вектор a задан в подвижной системе
отсчета OXYZ : a (t ) a (t ) i a (t ) j a (t ) k .
y
x
a
z
j
k
O1
x1
O
i
x
y1
y
z
Определим правило нахождения производной этого
вектора в неподвижной системе отсчета O1 X 1Y1Z1
(абсолютной производной), учитывая, что единичные
векторы i , j , k меняют свое направление
вследствие движения подвижной системы
отсчета OXYZ.
d ay
d a d ax
da
di
dj
dk
i
j z k ax
ay
az
dt
dt
dt
dt
dt
dt
dt
d ay
d ax
da
da
i
j zk
относительная производная вектора a .
Обозначим
dt
dt
dt
dt
di
dj
dk
i
,
j
,
k , поэтому выражение
По формуле Эйлера
dt
dt
dt
di
dj
dk
ay
az
(a x i a y j a z k ) a . Окончательно
dt
dt
dt
Абсолютная производная вектора равна сумме
da da
относительной производной и векторного
a
.
получим:
произведения угловой скорости подвижной
dt dt
системы отсчета на этот вектор.
2
ax
3.
ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙz1
z
k
O1
x1
где
y
M
Пусть точка М движется относительно подвижной системы отсчета OXYZ ,
которая совершает произвольное движение относительно неподвижной
системы отсчета O1 X1Y1Z1 . Положение точки М в подвижной системе
отсчета задается радиусом – вектором
r
j
O
O i
r , а в неподвижной системе
. Положение начала подвижной системы
отсчета задается радиусом – вектором O .
Тогда:
отсчета радиусом – вектором
t 0, O r , r x i y j z k .
y1
x Вектор абсолютной скорости точки М: V d d O d r ,
dt
dt
dt
d O
VO - скорость начала подвижной системы отсчета.
dt
dr dr
dr dx
dy
dz
пер r ,
i
j
k Vотн .
dt
dt
dt dt
dt
dt
V VO Vотн пер r (*). Переносную скорость точки М можно получить
из (*) , если зафиксировать положение точки в подвижной системе отсчета: положить
r const :
Vпер VO пер r . Заметим, что это скорость точки свободного твердого тела.
Окончательно
V Vпер Vотн (при пер 0, Vпер VO ).
Абсолютная скорость точки равна векторной сумме переносной и относительной скорости.
3
4.
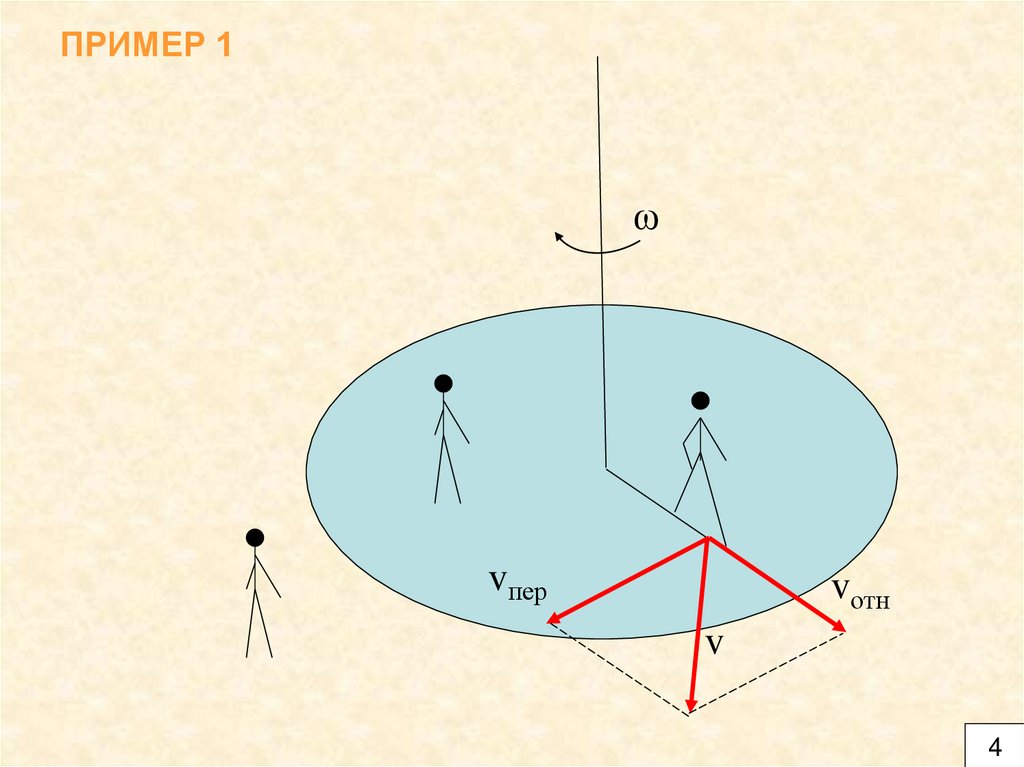
ПРИМЕР 1ω
vпер
vотн
v
4
5.
ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ(ТЕОРЕМА КОРИОЛИСА)
Для нахождения абсолютного ускорения точки М продифференцируем по времени выражение (*)
учитывая, что векторы V
и
заданы в подвижной системе отсчета.
отн
r
dV dVO dVотн d пер
d r где
a
r пер
,
dt
dt
dt
dt
dt
d пер
dVO
aO - ускорение начала подвижной системы отсчета;
r пер r ;
dt
dt
2
2
2
dVотн dVотн
d x
d y
d z
пер Vотн 2 i 2 j 2 k
dt
dt
dt
dt
dt
пер Vотн aотн пер Vотн ;
dr
dr
пер
пер (
пер r ) пер Vотн пер пер r .
dt
dt
a aO пер r пер пер r aотн 2 ( пер Vотн ) (**) .
Переносное ускорение точки М можно получить из выражения (**) положив в нем r const :
aпер aO пер r пер пер r .( пер пер 0 , aпер aO ) .
5
6.
ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ(ТЕОРЕМА КОРИОЛИСА)
Слагаемое 2 ( пер Vотн ) aкор называется Кориолисовым (поворотным)
ускорением.
Окончательно получим:
a aпер aотн aкор .
Теорема Кориолиса
Абсолютное ускорение точки равно векторной сумме ее переносного,
относительного и Кориолисова ускорений.
относительное ускорение точки характеризует изменение относительной
скорости в относительном движении;
переносное ускорение точки характеризует изменение переносной
скорости в переносном движении;
ускорение Кориолиса характеризует изменение относительной скорости
точки в переносном движении и переносной скорости точки в относительном
движении.
Оно возникает вследствие взаимного влияния движений, в которых
участвует точка.
6
7.
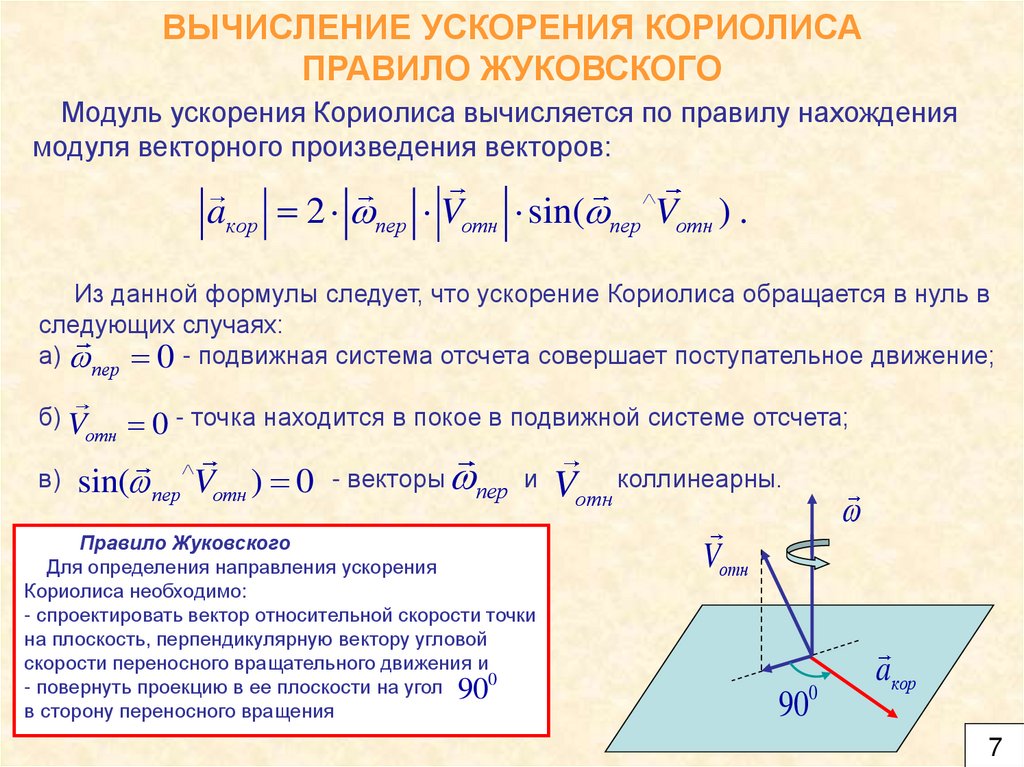
ВЫЧИСЛЕНИЕ УСКОРЕНИЯ КОРИОЛИСАПРАВИЛО ЖУКОВСКОГО
Модуль ускорения Кориолиса вычисляется по правилу нахождения
модуля векторного произведения векторов:
aкор 2 пер Vотн sin( пер Vотн ) .
Из данной формулы следует, что ускорение Кориолиса обращается в нуль в
следующих случаях:
а) пер 0 - подвижная система отсчета совершает поступательное движение;
б) V
отн
0 - точка находится в покое в подвижной системе отсчета;
в) sin(
пер
Vотн ) 0 - векторы пер и Vотн коллинеарны.
Правило Жуковского
Для определения направления ускорения
Кориолиса необходимо:
- спроектировать вектор относительной скорости точки
на плоскость, перпендикулярную вектору угловой
скорости переносного вращательного движения и
- повернуть проекцию в ее плоскости на угол 900
в сторону переносного вращения
Vотн
0
90
aкор
7
8.
РешениеПРИМЕР 2
M
φ(t)
O
1) ОМ = s(t1 ) 4 1 12 3( м);
2) По теореме о сложении скоростей:
V VПЕР VОТН
VПЕР ПЕР ОМ , VПЕР OM ;
d
2 t 3, ПЕР (t1 ) 2 1 3 1(c 1 ),
dt
ОМ = s(t) = 4t - t 2 (м);
VПЕР ПЕР ОМ 1 3 3 м ;
(t) = t 2 3t (рад);
с
t1 = 1c .
ds
VОТН
4 2 t ; VОТН (1) 4 2 1 2 м .
с
_______________
dt
2
2
VОТН VПЕР , поэтому V VОТН VОТН 22 32 3,6 м .
Найти:
с
V(t1 ) ? , a (t1 ) = ?
Дано:
ПЕР
M
VОТН
V
O
ω
VПЕР
8
9.
ПРИМЕР 2 (продолжение)y
3) По теореме о сложении ускорений:
a ПЕР
n
n
a aОТН
aОТН
a ПЕР aПЕР
aКОР .
M
dVОТН
2 м 2 ;
с
dt
2
VОТН
n
aОТН
0 т.к. траектория относительного
aОТН
ε aПЕР
O
aОТН
aКОР
ω
движения - прямая линия;
d
2(c 2 );
dt
a ПЕР 2 3 6 м 2 ;
с
VОТН
n
ОТН
a ПЕР OM , aПЕР
OM ;
x
a a a
6 4 2 м ,
с
a a a 5 2 5,39 м .
с
n
ax aОТН
aПЕР
2 3 5 м 2 ,
с
y
n
aПЕР
2 OM ( 1) 2 3 3 м 2 ;
с
ПЕР
2
x
2
y
2
2
2
2
aКОР 2 VОТН sin( , VОТН ) 2 1 2 1 4 м 2 .
с
Ответ: V=3,6 м ; a 5,39 м 2 .
с
с
КОР
9
10.
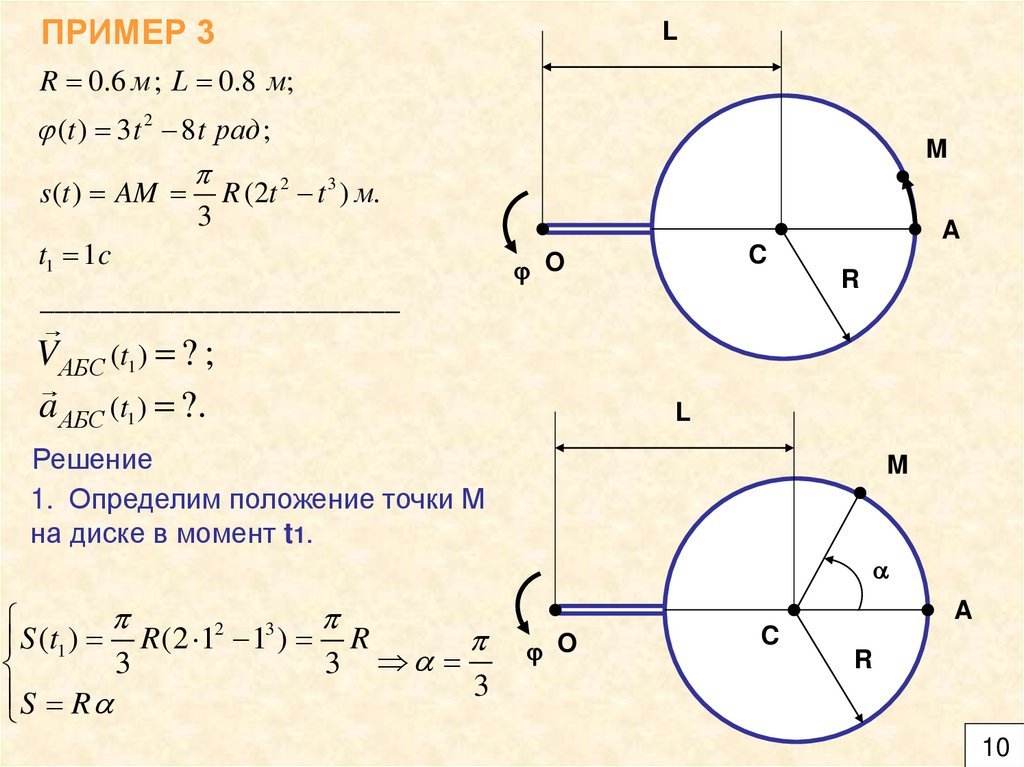
ПРИМЕР 3L
R 0.6 м ; L 0.8 м;
(t ) 3 t 2 8 t рад ;
2
s (t ) AM
3
M
R (2t t 3 ) м.
t1 1c
A
C
O
R
________________________
V АБС (t1 ) ? ;
a АБС (t1 ) ?.
L
Решение
1. Определим положение точки М
на диске в момент t1.
M
2
3
S
(
t
)
R
(2
1
1
)
R
1
3
3
3
S
R
A
O
C
R
10
11.
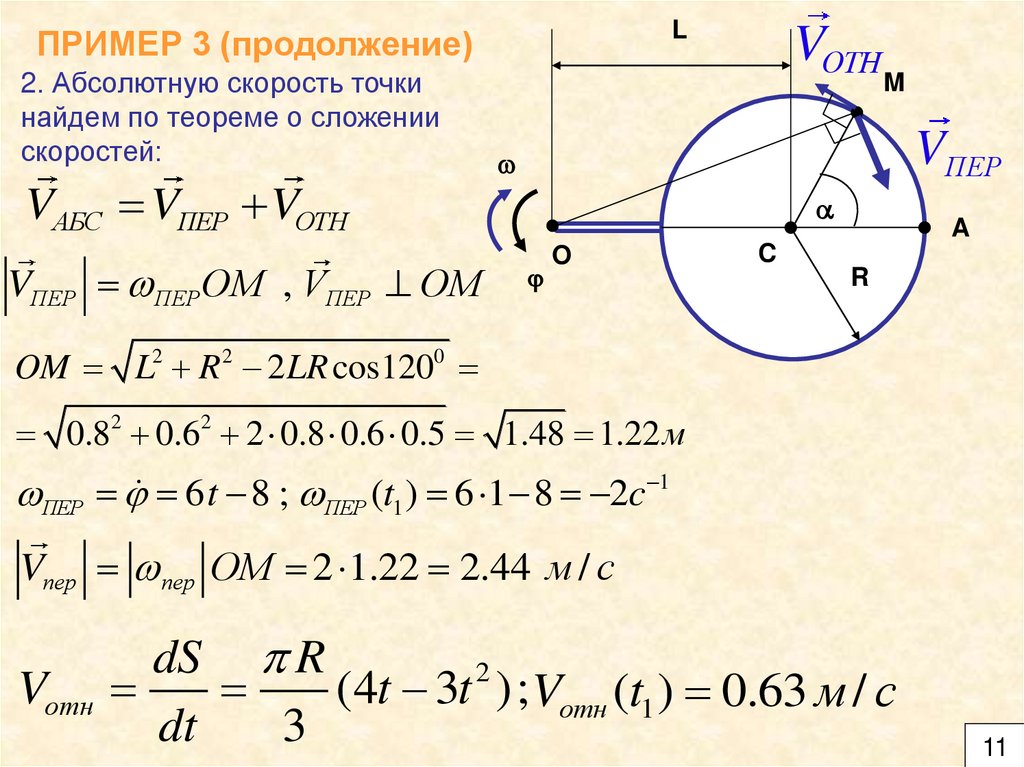
LПРИМЕР 3 (продолжение)
2. Абсолютную скорость точки
найдем по теореме о сложении
скоростей:
VАБС VПЕР VОТН
VПЕР ПЕР ОМ , VПЕР ОМ
VОТН
M
VПЕР
O
A
C
R
OM L2 R 2 2 LR cos1200
0.82 0.62 2 0.8 0.6 0.5 1.48 1.22 м
ПЕР 6 t 8 ; ПЕР (t1 ) 6 1 8 2c 1
Vпер пер ОМ 2 1.22 2.44 м / с
dS R
2
Vотн
(4t 3t ); Vотн (t1 ) 0.63 м / с
dt
3
11
12.
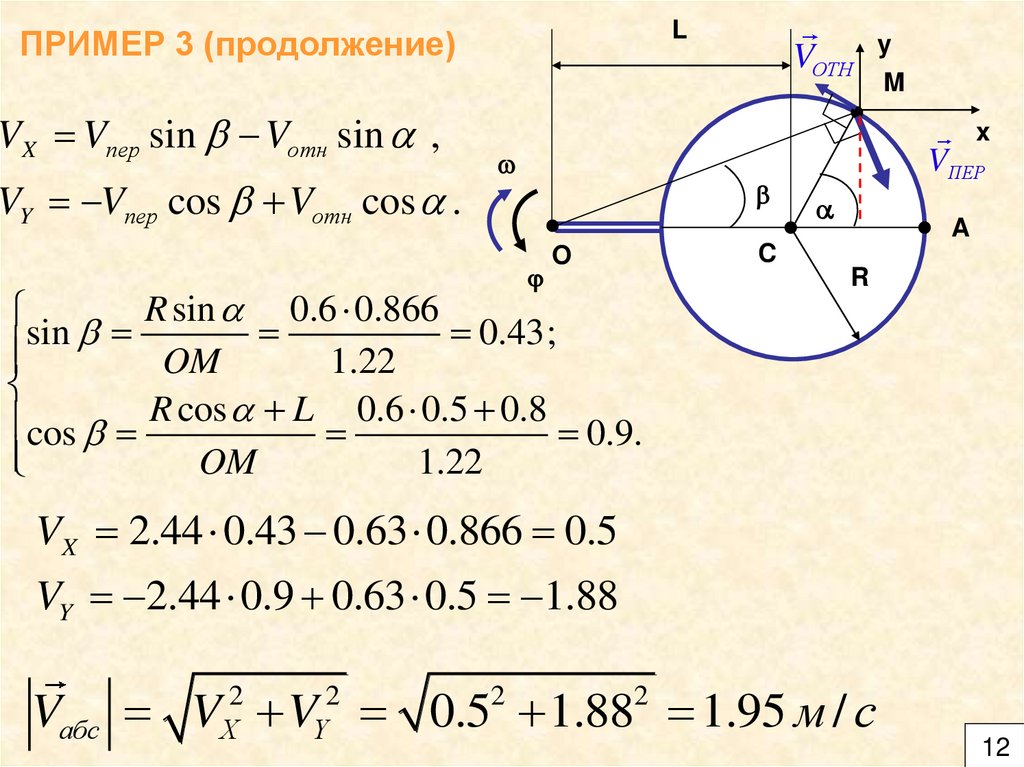
LПРИМЕР 3 (продолжение)
VОТН y
M
VX Vпер sin b Vотн sin ,
VY Vпер cos b Vотн cos .
x
b
VПЕР
A
C
O
R sin 0.6 0.866
sin b
0.43;
OM
1.22
cos b R cos L 0.6 0.5 0.8 0.9.
OM
1.22
R
VX 2.44 0.43 0.63 0.866 0.5
VY 2.44 0.9 0.63 0.5 1.88
Vабс V V 0.5 1.88 1.95 м / с
2
X
2
Y
2
2
12
13.
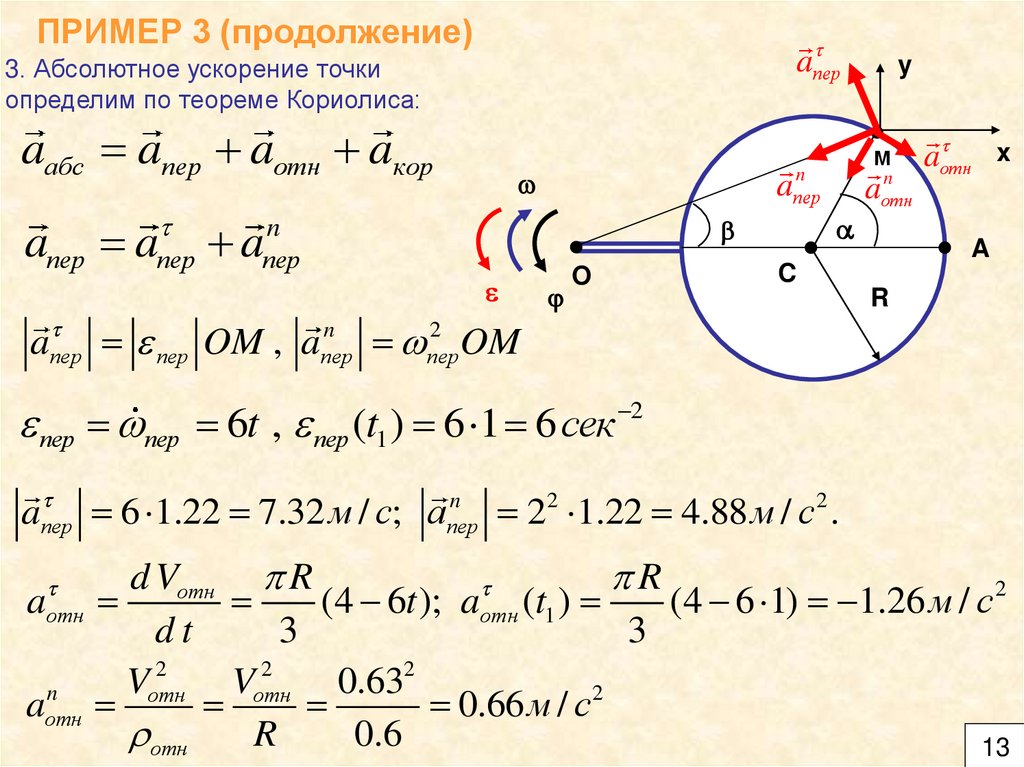
ПРИМЕР 3 (продолжение)aпер
3. Абсолютное ускорение точки
определим по теореме Кориолиса:
aабс aпер aотн aкор
aпер aпер a
n
пер
М
n
пер
a
b
O
y
n
aотн
aотн
x
A
C
R
n
2
aпер
пер OM , aпер
пер
OM
пер пер 6t , пер (t1 ) 6 1 6 сек 2
n
aпер
6 1.22 7.32 м / с; aпер
22 1.22 4.88 м / с 2 .
d Vотн R
R
aотн
(4 6t ); aотн (t1 )
(4 6 1) 1.26 м / с 2
dt
3
3
2
2
2
V
V
0.63
n
aотн
отн отн
0.66 м / с 2
отн
R
0.6
13
14.
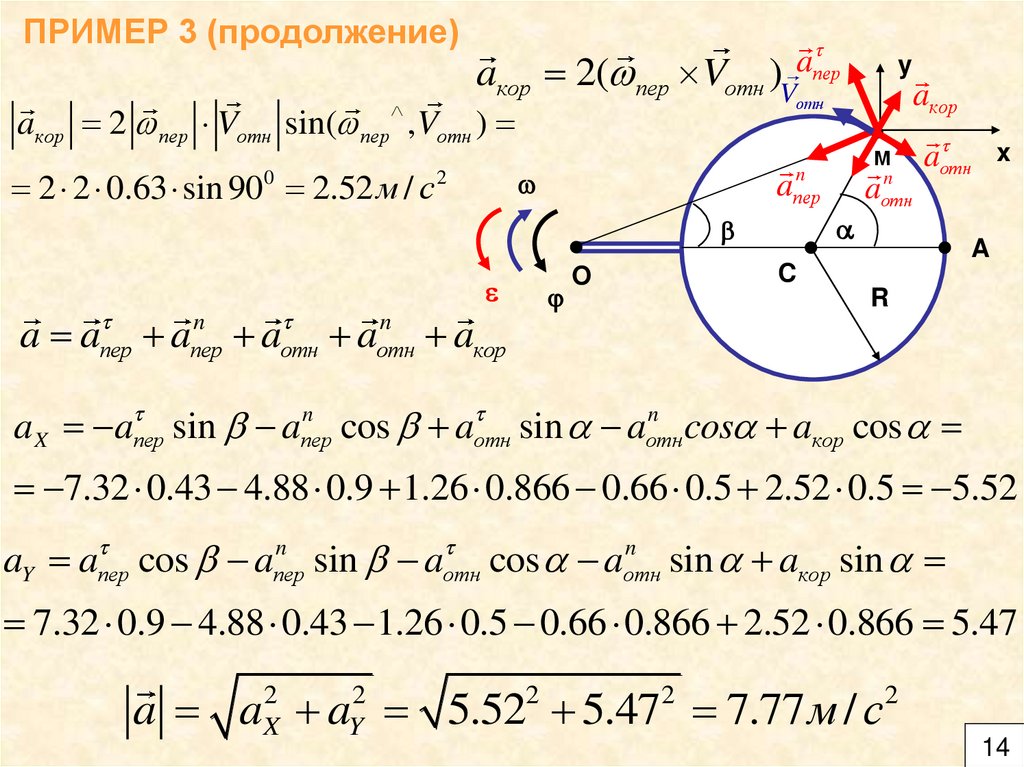
ПРИМЕР 3 (продолжение)a
) пер
aкор 2( пер Vотн V
aкор
отн
aкор 2 пер Vотн sin( пер ,Vотн )
2 2 0.63 sin 900 2.52 м / с 2
y
n
пер
a
b
n
n
a aпер
aпер
aотн
aотн
aкор
М
n
aотн
aотн
x
A
C
O
R
n
n
aX a пер sin b aпер
cos b aотн
sin aотн
cos aкор cos
7.32 0.43 4.88 0.9 1.26 0.866 0.66 0.5 2.52 0.5 5.52
n
n
aY a пер cos b aпер
sin b aотн
cos aотн
sin aкор sin
7.32 0.9 4.88 0.43 1.26 0.5 0.66 0.866 2.52 0.866 5.47
a a a 5.52 5.47 7.77 м / с
2
X
2
Y
2
2
2
14
15.
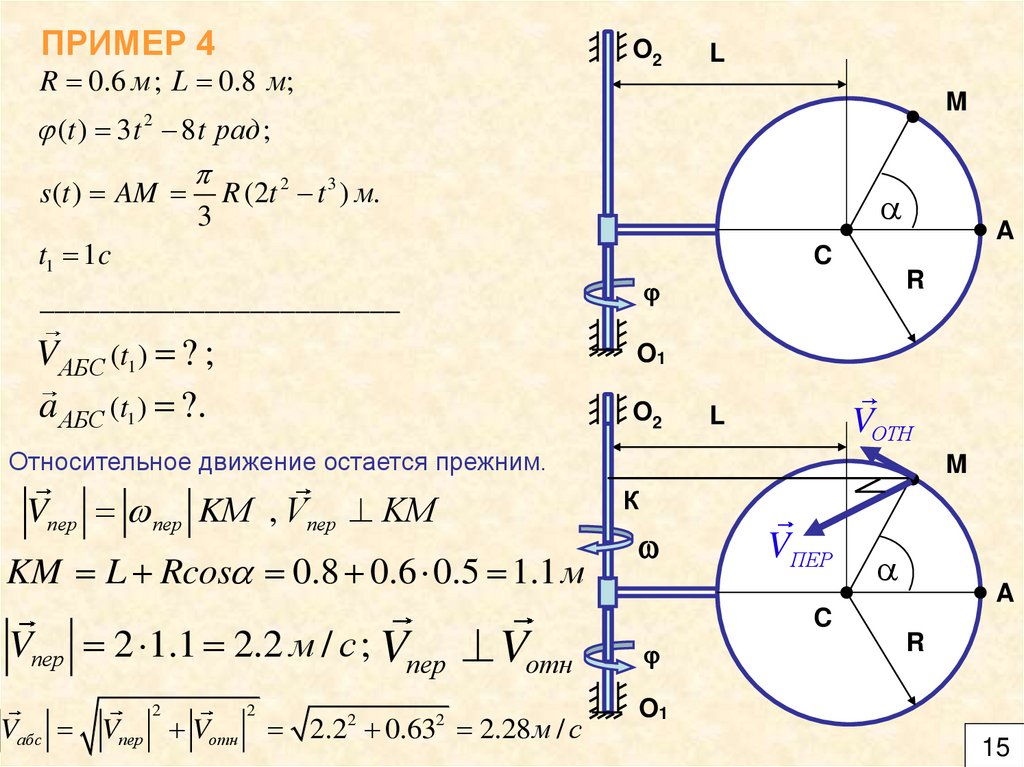
ПРИМЕР 4O2
R 0.6 м ; L 0.8 м;
L
M
(t ) 3 t 8 t рад ;
2
2
s (t ) AM
3
R (2t t 3 ) м.
t1 1c
A
C
R
________________________
V АБС (t1 ) ? ;
a АБС (t1 ) ?.
O1
O2
L
VОТН
Относительное движение остается прежним.
Vпер пер KМ , Vпер KМ
KM L Rcos 0.8 0.6 0.5 1.1 м
Vпер 2 1.1 2.2 м / с ; Vпер Vотн
2
Vабс Vпер Vотн
2
2.2 0.63 2.28 м / с
2
2
M
К
VПЕР
A
C
R
O1
15
16.
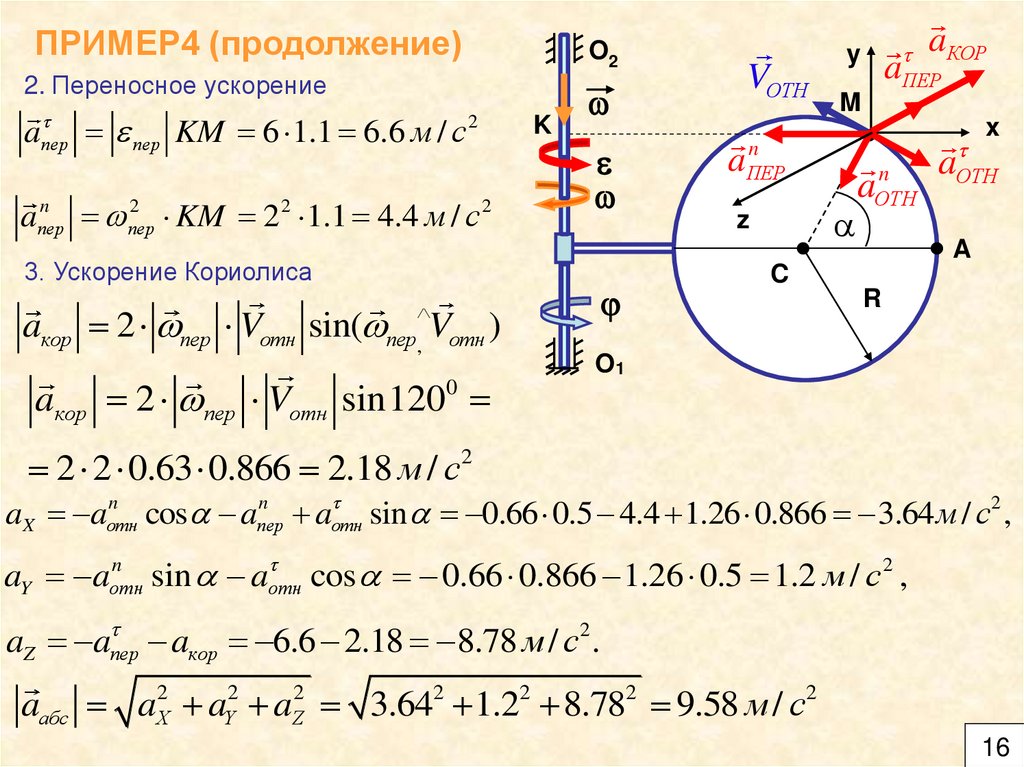
ПРИМЕР4 (продолжение)O2
2. Переносное ускорение
aпер пер KM 6 1.1 6.6 м / с
n
пер
a
2
пер
2
KM 2 1.1 4.4 м / с
2
K
2
3. Ускорение Кориолиса
aкор 2 пер Vотн sin( пер, Vотн )
aкор 2 пер Vотн sin1200
VОТН
a
aКОР
aПЕР
M
n
ПЕР
z
y
n
ОТН
a
x
aОТН
A
C
R
O1
2 2 0.63 0.866 2.18 м / с 2
n
n
aX aотн
cos aпер
aотн
sin 0.66 0.5 4.4 1.26 0.866 3.64 м / с2 ,
n
aY aотн
sin aотн
cos 0.66 0.866 1.26 0.5 1.2 м / с 2 ,
aZ a пер aкор 6.6 2.18 8.78 м / с2 .
aабс aX2 aY2 aZ2 3.642 1.22 8.782 9.58 м / с2
16
17.
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ИСТОРИИ НАУКИНикола́й Его́рович Жуко́вский
(5 (17) января 1847 с. Орехово,
ныне Владимирской области –
17 марта 1921, Москва)
Русский ученый-механик, создатель аэродинамики
как науки. Заслуженный профессор Московского
университета, профессор теоретической механики
Императорского Московского технического училища
(с 1918 г. — МВТУ). В 1894 г. Жуковский был избран
членом-корреспондентом Академии наук
по разряду математических наук . При его активном
участии были созданы Центральный аэрогидродинамический институт (ЦАГИ), Московский авиатехникум
( Военно-воздушная академия).
17
18.
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ИСТОРИИ НАУКИГюстав Гаспар Кориолис
(Coriolis G.G., 21.05.1792 – 19.09.1843)
Родился в Париже в 1792г.
В 1810 г. окончил Политехническую школу, а в 1812 г. Школу
мостов и дорог. С 1816 г. начал
преподавать в Политехнической
школе, где вскоре стал
профессором, а в 1831 г. –
директором учебной части
школы. Преподавал также в
Центральной школе искусств и
ремесел и в Школе мостов и
дорог. В 1836 г. был избран в
Парижскую академию наук
18









 Физика
Физика








