Сложное движение

1. Лекция №4

2.

Пусть т.Р – полюс, определим
скорости точек А и В.
v A vP v AP v AP , где v A v AP АР
vA
A
vВ vP vВP vВP , где v В v ВP ВР
В
P
vВ
Тогда, определив угловую скорость, получим следующее
соотношение:
vC
vA
vB
AP BP CP

3.

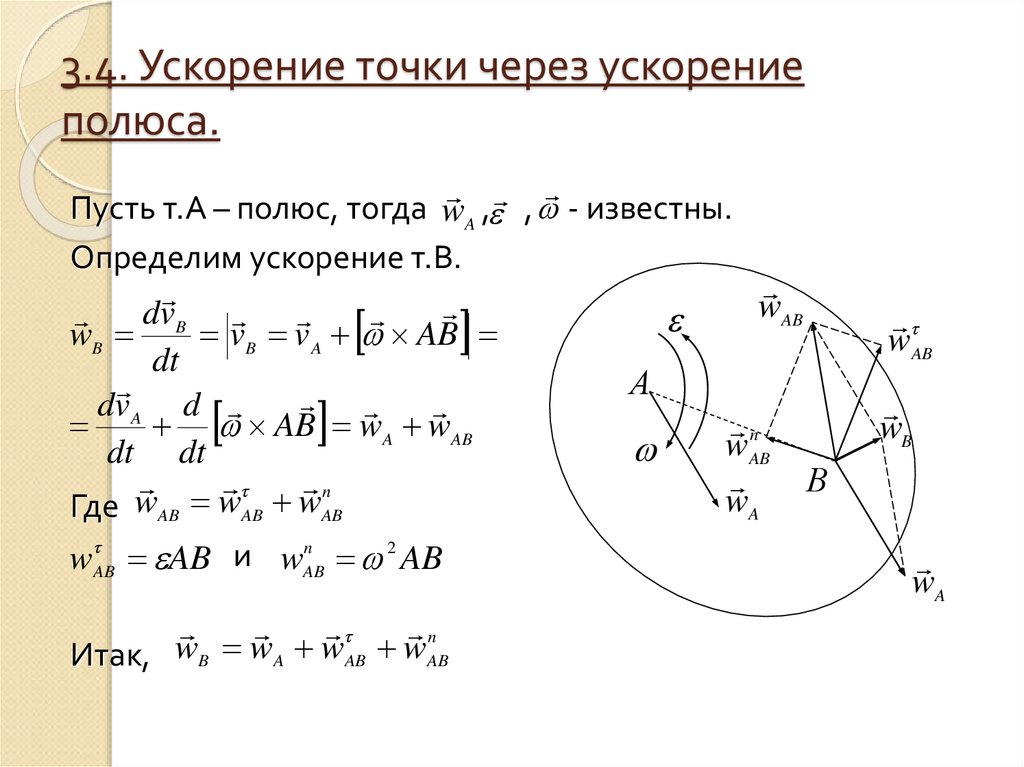
Способы нахождения мцс.

4. 3.4. Ускорение точки через ускорение полюса.

Пусть т.А – полюс, тогда wA , , - известны.
Определим ускорение т.В.
w
dv
AB
wB B vB v A AB
dt
А
dv
d
n
A AB wA wAB
wAB
dt dt
В
n
w
Где wAB wAB wAB
A
n
w AB AB и wAB
2 AB
n
w
w
w
w
Итак, B
A
AB
AB
w AB
wB
wA

5. 3.5. Мгновенный центр ускорения

Определение. Точка плоской фигуры, ускорение
которой в данный момент времени равно 0,
называется мгновенными центром ускорения (мцу).
Теорема. 1) Если угловая скорость и ускорение
плоской фигуры в данный момент времени
одновременно не равны 0, то мцу существует и
единственен.
2) Если угловая скорость и ускорение плоской фигуры
в данный момент времени одновременно равны 0,
то ускорения точек в данный момент времени
совпадают и мцу не существует.

6.

Способ нахождения мцу.
Если 4 2 0 тогда arctg
2
n
n
4
2
w
AP
wА wР w AР wAР
w AР wAР
и A
n
n
wВ wР wВР wВР wВР wВР и wB BP 4 2
1. Если 0 и 0 , тогда 0
А
2. Если 0 и 0 , тогда / 2
wA
В
P
wB

7. Сложное движение МТ

Основные понятия и определения.
Определение. Движение точки, при котором она
участвует в двух или более движениях
одновременно, называется сложным.
1.
z1
Определение. Движение точки
относительно неподвижной
системы отсчета называется
абсолютным (rM ).
z
rM
O1
x1
rO
M
y
O
x
y1

8.

Определение. Движение точки относительно подвижной
системы отсчета называется относительным ( ) и
обозначается индексом r (relativus (лат.) относительный).
Определение. Движение подвижной системы отсчета
относительно неподвижной называется переносным ( r O ) и
обозначается индексом e (entraner (лат) – увлекать за
собой).
Тогда вектор абсолютного движения представим в виде:
rM rO , где xi yj zk

9. 2. Формула Бура

Определение. Полной производной по времени
вектора
, заданного в подвижной системе координат,
d
называют вектор dt , связанный с вычислением этой
производной относительно неподвижной системы
координат.
Определение.
Частной производной по времени
вектора , заданного в подвижной системе
координат, называют вектор t , связанный с
вычислением этой производной относительно
подвижной системы координат.

10.

d d ( xi yj zk )
dt
dt
di
dj
dk
x i y j z k x y z
dt
dt
dt
x e i y e j z e k
t
e ( xi yj zk )
e
t
t
d
e - формула Бура
dt t

11. 3. Абсолютная скорость и абсолютное ускорение точки.

Определение. Абсолютной скоростью (ускорением) т. М,
участвующей в сложном движении, называется ее
скорость (ускорение) относительно неподвижной
системы координат.
Определим абсолютную скорость:
dr
d drO
dr
, где
v M rM rO O
e
dt
dt
dt
dt
t
d
r
e e
O
ve
e vO vOM - компоненты переносного
dt
движения

12.

vr
t
- компонента относительного движения
Тогда абсолютная скорость: v vr ve
Определим абсолютное ускорение:
dv0 d dvr
dv d dr0
w
e vr
e
dt dt dt
dt dt
dt
e d vr
wO e e
e vr
dt t
v
wOe wOM
e e e r e vr
e
t
e
e
wOe wOM
wOM
wr 2 e vr
t

13.

Теорема Кориолиса. Абсолютное ускорение точки
складывается из относительного, переносного
ускорения, а также ускорения Кориолиса:
w wr we wK , где
2
v
r
wr
2 - компонента относительного
t
t
движения,
dv O
-
e e
e
we wO wOM wOM
e e e
dt
- компонента переносного движения,
wK 2 e vr
- ускорение Кориолиса

14. 4. Ускорение Кориолиса. Правило Жуковского.

Определение. Ускорение Кориолиса – это вектор,
равный удвоенному векторному произведению
вектора угловой скорости переносного вращения на
вектор скорости относительного движения.
Длина вектора определяется по формуле:
wK 2 e vr sin( e , vr )

15.

Правило Жуковского.
1. Строим плоскость, перпендикулярную вектору
угловой скорости: e
.
2. Проецируем на эту плоскость вектор относительной
плоскости: a пр vr
3. Поворачиваем полученный вектор на угол 90
градусов в сторону вращения угловой скорости:
a1 a, a1
4. Полученный вектор восстанавливаем при помощи
параллельного переноса до точки М. Получим
вектор ускорения Кориолиса: w
a
K
1

16.

Правило правой руки
vr
wK
e
e

17.

Частные случаи:
1.
2.
Если переносное движение является
поступательным, то e 0 и wK 0 .
Если e v r , то wK 0