Множества чисел. Свойства действительных чисел

1.

Тема урока:

2.

Объединением множеств А и В называют
множество, состоящее из всех элементов,
принадлежащих хотя бы одному из этих множеств.
A B
Пересечением множеств А и В
называют множество, состоящее из всех
элементов, каждый из которых
принадлежит и множеству А, и множеству
В.
A B
2

3.

Свойства порядка.
№
1
2
3
свойство
Для любых двух действительных
чисел а и b выполняется, и
притом только одно из трех,
соотношение: a=b, a<b, a>b
Для любых двух действительных
чисел a и b, таких, что a<b,
найдется такое действительное
число с, что a<c и c<b, т.е. a<c<b
Если a<b и b<c, то a<c

4.

Свойства сложения и вычитания.
№
1
2
свойство
a+b=b+a (переместительное
свойство сложения)
(a+b)+c=a+(b+c) (сочетательное
свойство сложения).
3
a+0=a.
4
a+(-a)=0.
5
a-b=a+(-b).
6
Если a<b, то a+c<b+c для любого
действительного числа с.

5.

Свойства умножения и деления.
№
свойство
1
a b=b a (переместительное свойство умножения)
2
4
(a b) c=a (b c) (сочетательное свойство умножения).
a 1 =a.
a 0=0.
5
-a=(-1) a .
6
a
3
7
8
1
1(a 0)
a
1 a
a (b 0)
b b
(a+b) c =a c + b c (распределительное свойство
умножения).
9
Если a<b и с- положительное число, то ac<bc.

6.

Архимедово свойство.
Для любых чисел a и b, таких, что b>a>0,
существует натуральное число n, такое, что
an>b.

7.

Свойство непрерывности действительных
чисел.
Для любой системы отрезков a1; b1 , a2 ; b2 , , an ;b n ,
удовлетворяющей условиям :
1) a1 a2 an an 1 bn 1 bn b2 b1 ;
2) bn an 0 при n ,
существует, и притом единственная, точка,
принадлежащая всем отрезкам an ; bn .

8.

Таблица числовых промежутков
Геометрическая модель
a
х
a
х
b
х
b
х
a
b
х
a
b
х
a
b
х
Обозначение
Название
числового
промежутка
Аналитическая
модель
(a; )
Открытый луч
х a
a;
Луч
х a
( ; b)
Открытый луч
х b
; b
Луч
х b
( a; b )
Интервал
a x b
a; b
Отрезок
a x b
(a; b
Полуинтервал
a x b

9.

Заполните таблицу
Геометрическая
модель
?
1
3
2
2
?
5
?
-3
-2
2
Название
числового
промежутка
Аналитическая
модель
х
1; 3
Отрезок
?
1 x
? 3
х
2;?
?
Луч
?2
х
(2;
? 5)
Интервал
?
2 x 5
( ?; 3)
Открытый луч
х ? 3
х
х
2
?
Обозначение
х
2;? 2
х
2;
от до 3
Полуинтервал
?
2 ?x 2
Открытый луч
х ? 2
?
от 2 до

10.

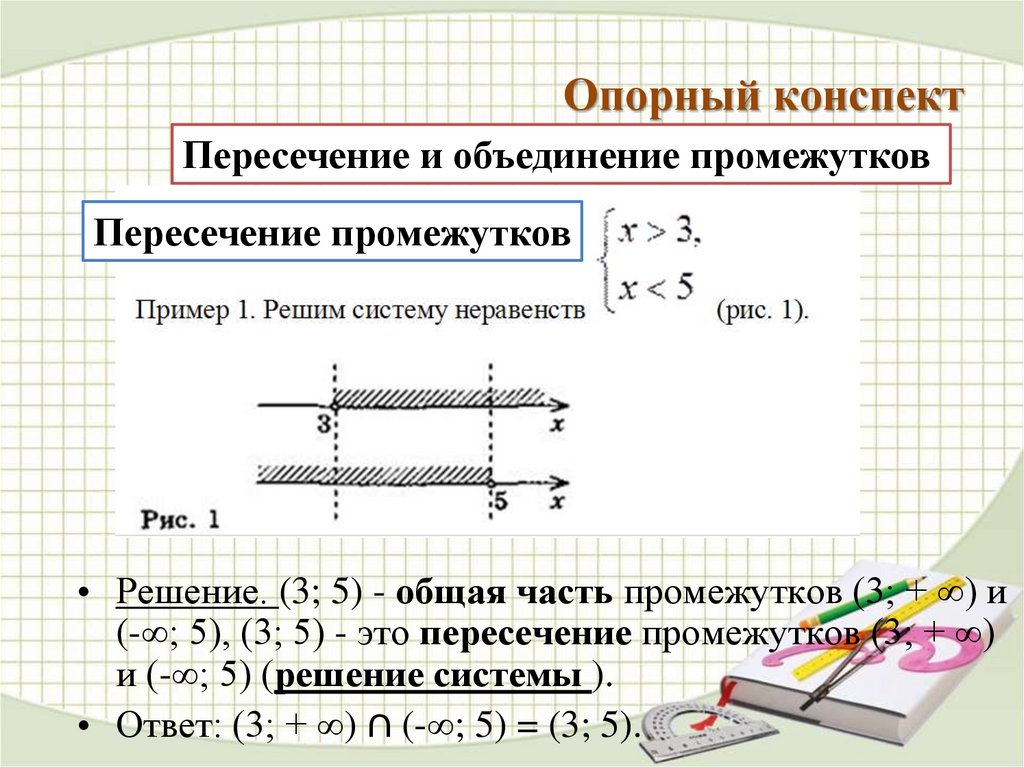
Опорный конспект
Пересечение и объединение промежутков
Пересечение промежутков
• Решение. (3; 5) - общая часть промежутков (3; + ∞) и
(-∞; 5), (3; 5) - это пересечение промежутков (3; + ∞)
и (-∞; 5) (решение системы ).
• Ответ: (3; + ∞) ∩ (-∞; 5) = (3; 5).

11.

Опорный конспект
Пересечение и объединение промежутков
Объединение промежутков
• Решение. Промежуток (-1; 3) состоит из чисел, которые
являются решением хотя бы одного из неравенств 2 < х < 3
или -1 < х < 2,5, поэтому является объединением этих
промежутков (решением совокупности).
• Ответ: (2; 3) ∪ (-1; 2,5) = (-1; 3).

12.

• Дома:
• 1.22, 1.23, 1,24, 1,26,1.27
Учитель математики МБОУ СОШ
№ 25 г. Крымска Е.В. Малая