Графики функций

1.

27.09.22
Графики функций

2.

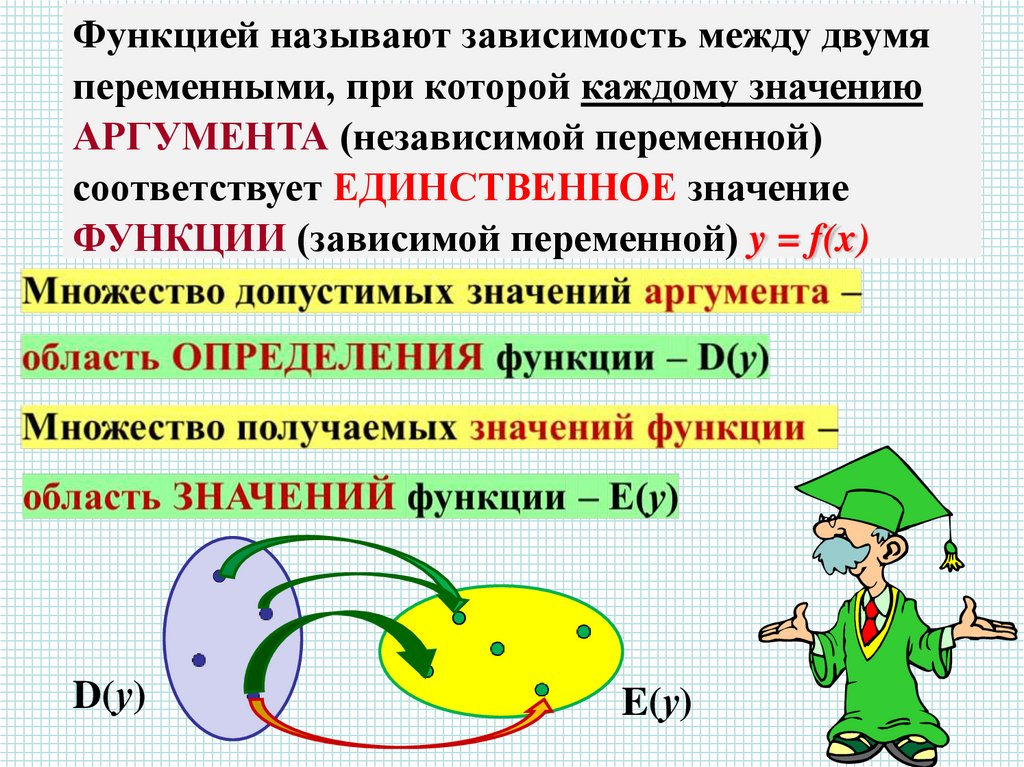
Функцией называют зависимость между двумя
переменными, при которой каждому значению
АРГУМЕНТА (независимой переменной)
соответствует ЕДИНСТВЕННОЕ значение
ФУНКЦИИ (зависимой переменной) y = f(x)
D(у)
E(у)

3.

Способы задания функции
Аналитический (формула)
Табличный (в виде таблицы)
Графический (график)
Описательный (соответствие множеств)

4.

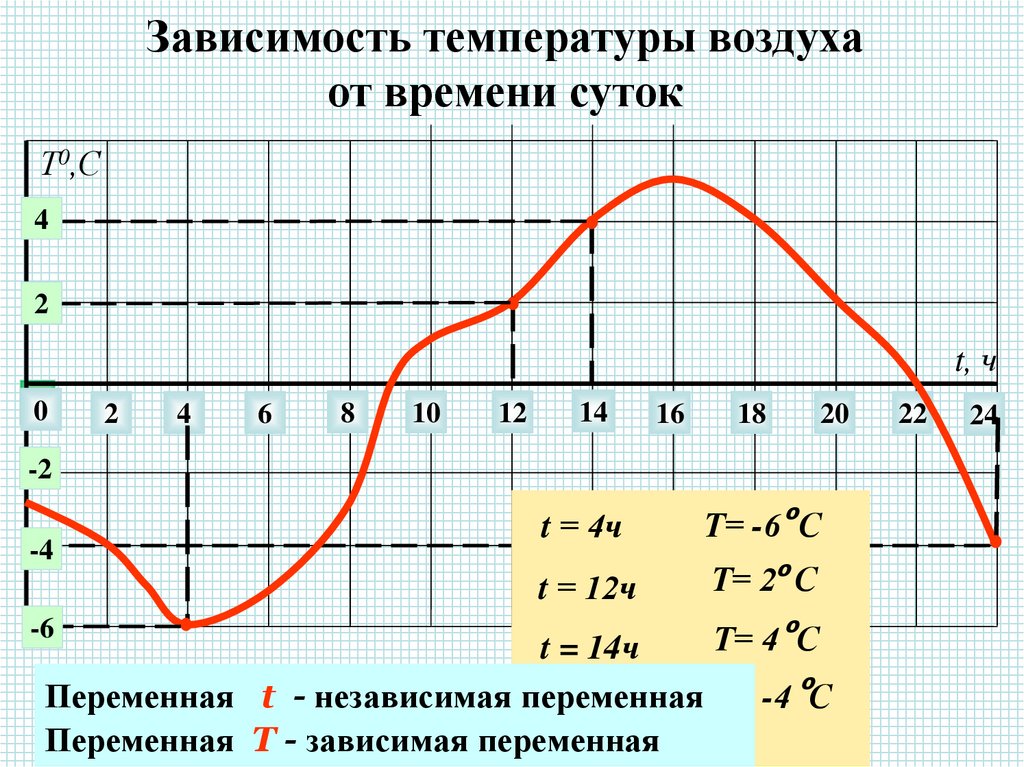
Зависимость температуры воздуха
от времени суток
Т0,С
4
2
t, ч
0
2
4
6
8
10
12
14
16
18
20
-2
-4
-6
t = 4ч
Т= -6 оС
t = 12ч
Т= 2о С
о
Т= 4 С
t = 14ч
о
Переменная t - независимая переменная
Т=
-4
С
t = 24ч
Переменная T - зависимая переменная
22
24

5.

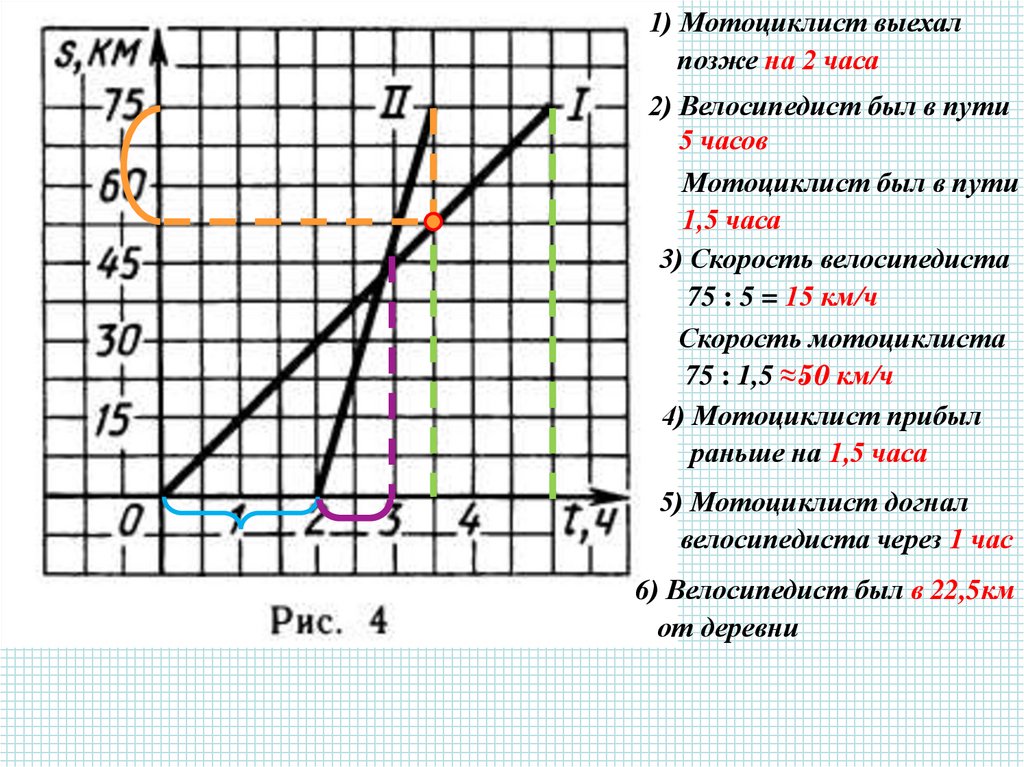
1) Мотоциклист выехал
позже на 2 часа
2) Велосипедист был в пути
5 часов
Мотоциклист был в пути
1,5 часа
3) Скорость велосипедиста
75 : 5 = 15 км/ч
Скорость мотоциклиста
75 : 1,5 ≈50 км/ч
4) Мотоциклист прибыл
раньше на 1,5 часа
5) Мотоциклист догнал
велосипедиста через 1 час
6) Велосипедист был в 22,5км
от деревни

6.

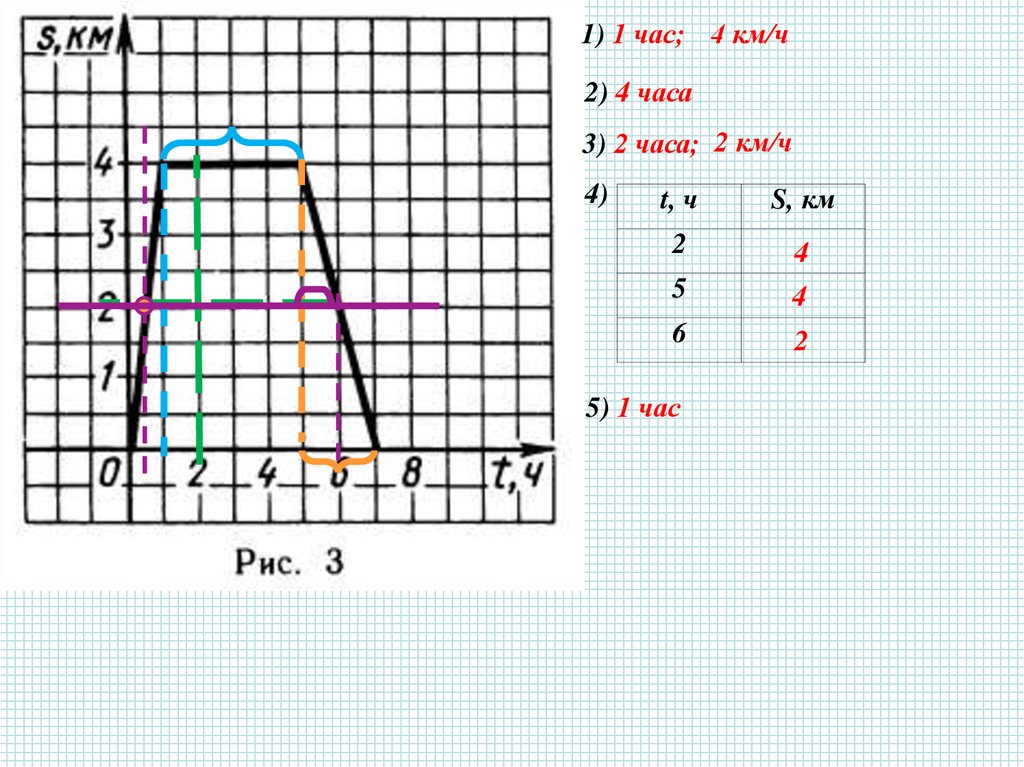
1) 1 час; 4 км/ч
2) 4 часа
3) 2 часа; 2 км/ч
4)
t, ч
S, км
2
4
5
4
6
2
5) 1 час

7.

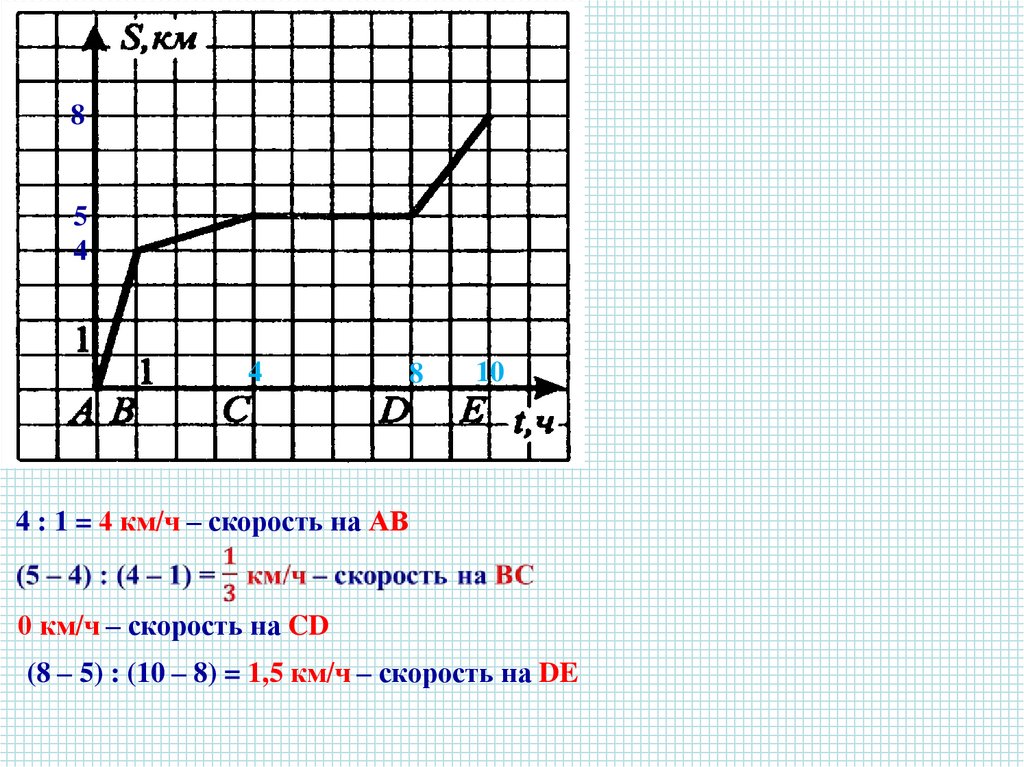
8
5
4
4
8
10
4 : 1 = 4 км/ч – скорость на АВ
0 км/ч – скорость на CD
(8 – 5) : (10 – 8) = 1,5 км/ч – скорость на DE

8.

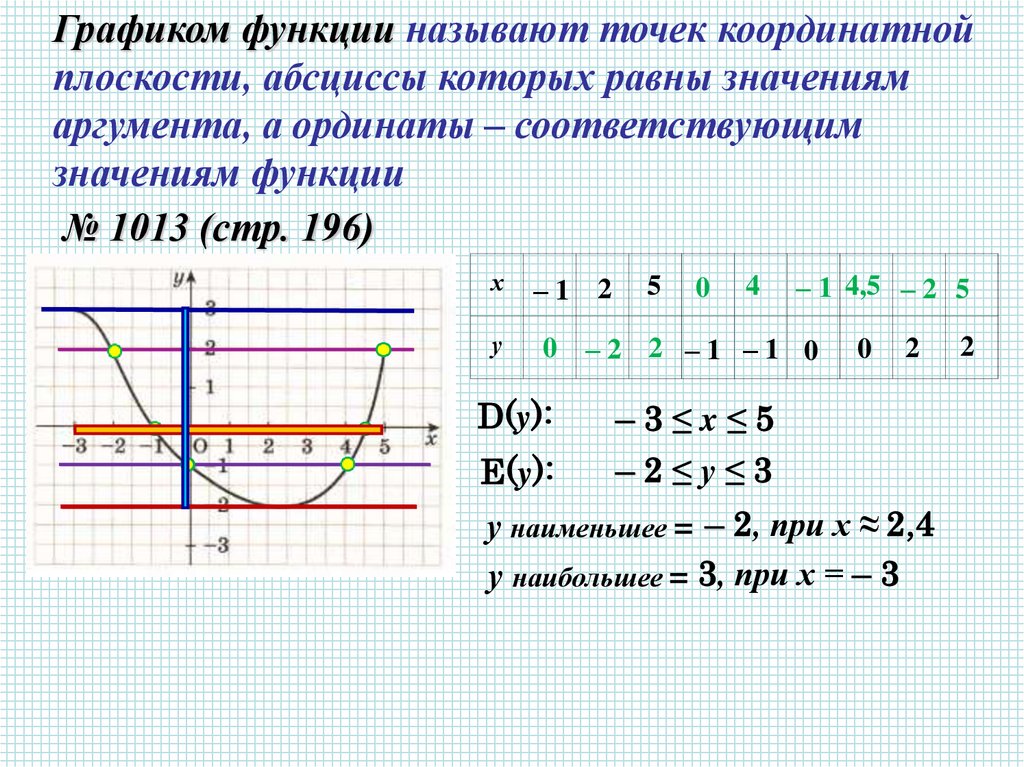
Графиком функции называют точек координатной
плоскости, абсциссы которых равны значениям
аргумента, а ординаты – соответствующим
значениям функции
№ 1013 (стр. 196)
х
–1 2
у
0
5
0
4
– 1 4,5 – 2 5
–2 2 –1 –1 0
D(y):
–3≤x≤5
E(y):
–2≤у≤3
0
2
у наименьшее = – 2, при х ≈ 2,4
у наибольшее = 3, при х = – 3
2

9.

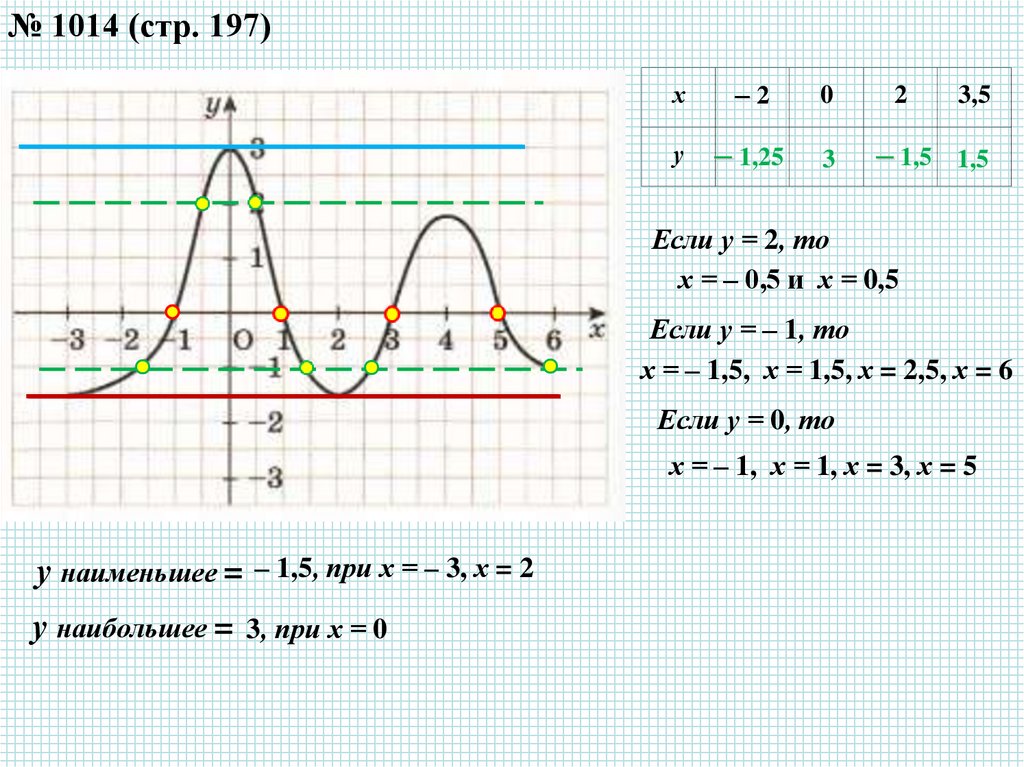
№ 1014 (стр. 197)
х
–2
0
2
3,5
у
– 1,25
3
– 1,5
1,5
Если у = 2, то
х = – 0,5 и х = 0,5
Если у = – 1, то
х = – 1,5, х = 1,5, х = 2,5, х = 6
Если у = 0, то
х = – 1, х = 1, х = 3, х = 5
у наименьшее = – 1,5, при х = – 3, х = 2
у наибольшее = 3, при х = 0

10.

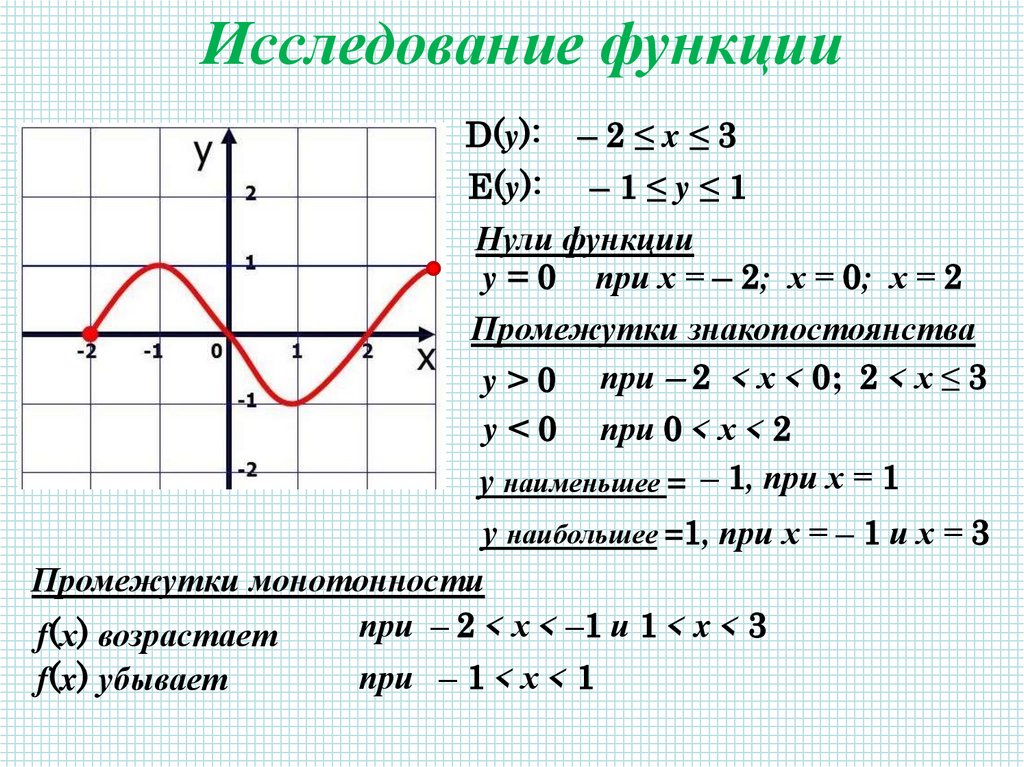
Исследование функции
D(y):
–2≤x≤3
E(y):
–1≤y≤1
Нули функции
y = 0 при х = – 2; х = 0; х = 2
Промежутки знакопостоянства
y > 0 при – 2 < х < 0; 2 < х ≤ 3
y<0
при 0 < х < 2
у наименьшее = – 1, при х = 1
у наибольшее =1, при х = – 1 и х = 3
Промежутки монотонности
при – 2 < х < –1 и 1 < x < 3
f(х) возрастает
f(x) убывает
при – 1 < х < 1

11.

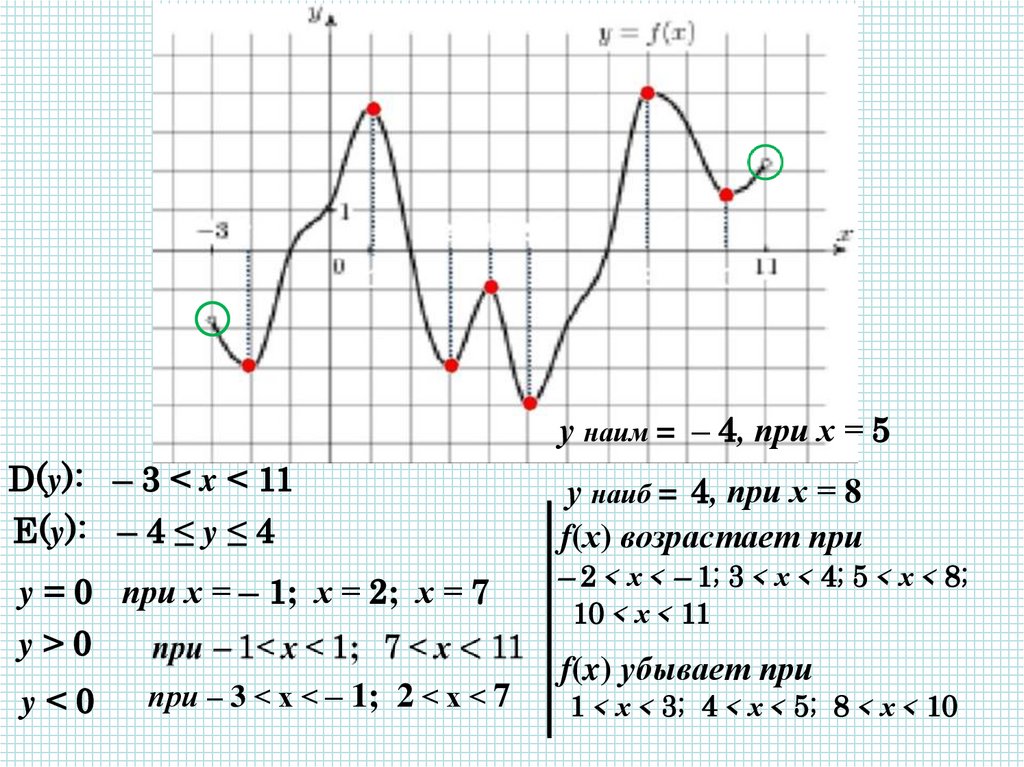
у наим = – 4, при х = 5
D(y): – 3 < x < 11
E(y): – 4 ≤ y ≤ 4
y = 0 при х = – 1; х = 2; х = 7
y>0
y<0
при – 3 < х < – 1; 2 < х < 7
у наиб = 4, при х = 8
f(х) возрастает при
– 2 < х < – 1; 3 < х < 4; 5 < х < 8;
10 < х < 11
f(x) убывает при
1 < х < 3; 4 < х < 5; 8 < х < 10

12.

Решите задачу, составив уравнение.
Некоторое расстояние автобус проехал за 4 ч, а автомобиль - за 3 ч.
Чему равно это расстояние, если скорость автомобиля на 12 км/ч
больше скорости автобуса?
Автобус
Автомобиль
Ʋ, км/ч
t, ч
S, км
х
х – 12
3
3х
4(х – 12)
4(х – 12) = 3х
4х – 48 = 3х
х = 48
48 км/ч – скорость автобуса
3 ∙ 48 = 144 км – искомое расстояние
Ответ: 144 км
4

13.

Домашнее задание
1) § 14 п.35 (стр. 193)
2) № 1015, 1018,
№ 1021 (+ исследование функции по графику)