Скрытые марковские модели. Разрешение морфологической неоднозначности

1. Скрытые марковские модели

Разрешение морфологической
неоднозначности

2. Постморфологический анализ

• =предсинтаксический анализ
• Предназначен для устранения морфологической
омонимии (многозначности) слов
–Выбор правильной леммы
–Уточнение морфологических характеристик
Основные методы
- Написание правил,
- Статистические методы, прежде всего, на основе
морфологически размеченного корпуса
-Скрытые марковские модели

3. Марковские модели

• Набор состояний: {s , s , , s }
1 2
N
• Процесс движется от одного состояния к другому,
порождая последовательность состояний :
si1 , si 2 , , sik ,
•Свойство марковской цепи: вероятность следующего
состояния зависит от состояния предыдущего:
P(sik | si1 , si 2 , , sik 1 ) P(sik | sik 1 )
• Чтобы определить марковскую сеть, должны быть
определены следующие вероятности
i P( si )
aij P( si | s j )

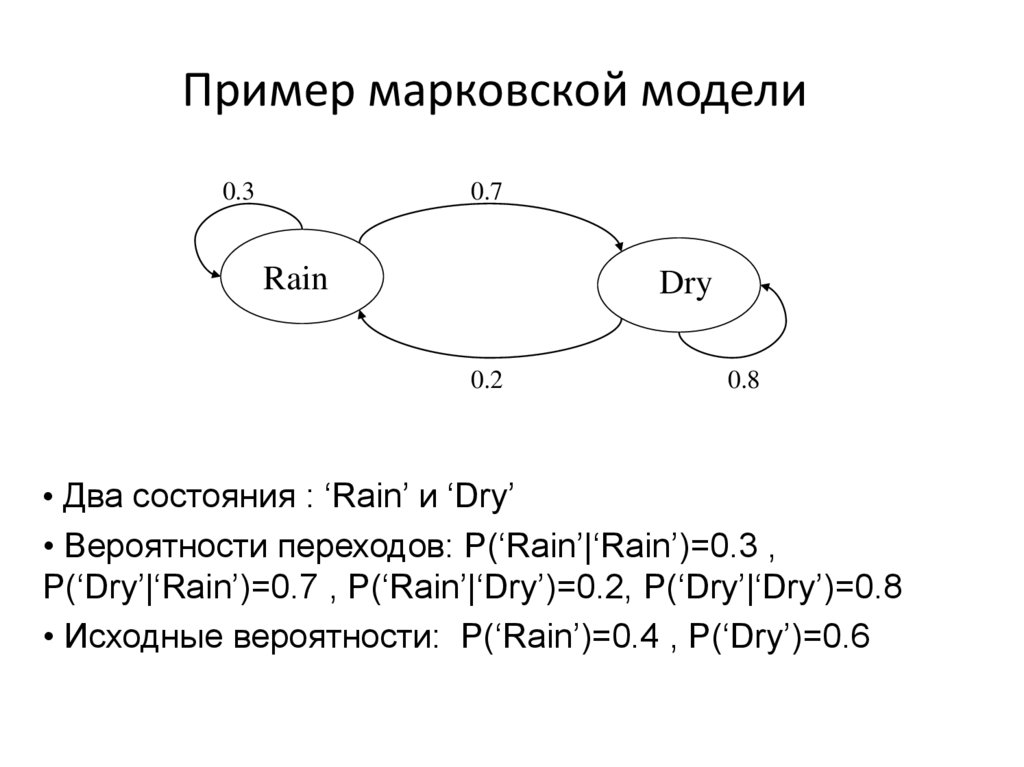
4. Пример марковской модели

0.3
0.7
Rain
Dry
0.2
0.8
• Два состояния : ‘Rain’ и ‘Dry’
• Вероятности переходов: P(‘Rain’|‘Rain’)=0.3 ,
P(‘Dry’|‘Rain’)=0.7 , P(‘Rain’|‘Dry’)=0.2, P(‘Dry’|‘Dry’)=0.8
• Исходные вероятности: P(‘Rain’)=0.4 , P(‘Dry’)=0.6

5. Вычисление вероятности последовательности

• По свойству марковской цепи, вероятность
последовательности состояний может быть найдена по
формуле
P( si1 , si 2 , , sik ) P( sik | si1 , si 2 , , sik 1 ) P( si1 , si 2 , , sik 1 )
P( sik | sik 1 ) P( si1 , si 2 , , sik 1 )
P( sik | sik 1 ) P( sik 1 | sik 2 ) P( si 2 | si1 ) P( si1 )
• Предположим, мы хотим подсчитать вероятность
последовательности: {‘Dry’,’Dry’,’Rain’,Rain’}.
P({‘Dry’,’Dry’,’Rain’,Rain’} ) =
P(‘Rain’|’Rain’) P(‘Rain’|’Dry’) P(‘Dry’|’Dry’) P(‘Dry’)=
= 0.3*0.2*0.8*0.6

6. Скрытые марковские модели

{s1 , s2 , , sN }
• Множество состояний:
•Процесс движется от состояния к состоянию :
• Выполняется свойство марковской цепи:
• Состояния – невидимы, но каждое состояние
порождает одно из M наблюдений - видимых состояний
{v1 , v2 , , vM }
•Чтобы определить скрытую марковскую цепь, нужно
определить
• Матрицу переходов A=(aij), aij= P(si | sj) ,
• Матрицу вероятностей наблюдаемых состояний
B=(bi (vm )), bi(vm ) = P(vm | si)
• Вектор начальных вероятностей =( i), i = P(si).
• Модель представлена M=(A, B, ).

7. Пример скрытой марковской модели

0.3
0.7
Low
High
0.2
0.6
Rain
0.4
0.8
0.4
0.6
Dry

8. Пример скрытой марковской модели

• Два состояния: ‘Низкое’ and ‘Высокое’ атм. давление.
• Два наблюдения: ‘Дождь’ and ‘Сухо’.
• Вероятности перехода: P(‘Low’|‘Low’)=0.3 ,
P(‘High’|‘Low’)=0.7 , P(‘Low’|‘High’)=0.2,
P(‘High’|‘High’)=0.8
• Вероятности наблюдения: P(‘Rain’|‘Low’)=0.6 ,
P(‘Dry’|‘Low’)=0.4 , P(‘Rain’|‘High’)=0.4 ,
P(‘Dry’|‘High’)=0.3 .
• Начальные вероятности: P(‘Low’)=0.4 , P(‘High’)=0.6 .

9. Пример вычисления вероятности наблюдений

• Хотим вычислить вероятность последовательности,
{‘Dry’,’Rain’}.
•Рассмотрим все возможные скрытые состояния:
P({‘Dry’,’Rain’} ) = P({‘Dry’,’Rain’} , {‘Low’,’Low’}) +
P({‘Dry’,’Rain’} , {‘Low’,’High’}) + P({‘Dry’,’Rain’} ,
{‘High’,’Low’}) + P({‘Dry’,’Rain’} , {‘High’,’High’})
где первый элемент:
P({‘Dry’,’Rain’} , {‘Low’,’Low’})=
P({‘Dry’,’Rain’} | {‘Low’,’Low’}) P({‘Low’,’Low’}) =
P(‘Dry’|’Low’)P(‘Rain’|’Low’) P(‘Low’)P(‘Low’|’Low)
= 0.4*0.6*0.4*0.3

10. Почему важно рассмотрение HMM в автоматической обработке текста

• Непосредственно имеем дело с неоднозначными
словами и конструкциями
• Нужно распознавать скрытые
– Части речи
– Лексические значения
– Типы именованных сущностей (организация,
персона, географическое место …)
– Определение тональности предложения
– и др.

11. Что такое HMM?

• Графическая модель
• Кружки – это состояния
• Стрелки обозначают вероятностные
зависимости между состояниями

12. Что такое HMM?

• Зеленые кружки – это скрытые состояния
• Зависят только от предыдущего состояния

13. Что такое HMM?

• Фиолетовые кружки – это наблюдаемые
состояния
• Зависят только от соответствующих
скрытых состояний

14. HMM формализм

S
S
S
S
S
K
K
K
K
K
• {S, K, P, A, B}
• S : {s1…sN } - значения скрытых состояний
• K : {k1…kM } – значения наблюдаемых состояний

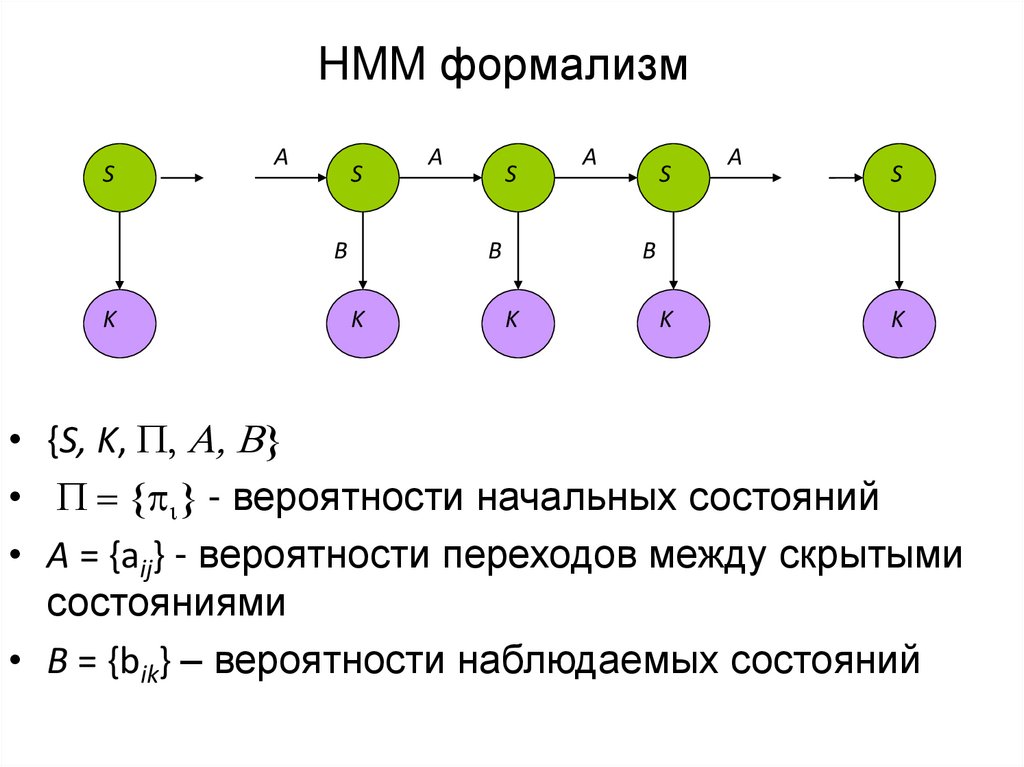
15. HMM формализм

S
A
S
B
K
A
S
B
K
A
S
A
S
B
K
K
K
• {S, K, P, A, B}
• P { i} - вероятности начальных состояний
• A = {aij} - вероятности переходов между скрытыми
состояниями
• B = {bik} – вероятности наблюдаемых состояний

16. Вывод HMM

• Вычислить вероятность последовательности
наблюдаемых состояний (Evaluation)
• Имея последовательность наблюдаемых состояний,
вычислить наиболее вероятную последовательность
скрытых состояний (Decoding)
• Имея последовательность наблюдаемых состояний и
множество возможных моделей, определить какая
модель лучше соответствует данным (т.е. наблюдаемой
последовательности) (Learning)

17. Оценка (Evaluation)

o1
ot-1
ot
ot+1
oT
Имея последовательность наблюдаемых состояний
и модель, вычислить вероятность
последовательности наблюдаемых состояний
O (o1...oT ), ( A, B, P )
Вычислить P(O | )

18. Оценка (Evaluation)

x1
xt-1
xt
xt+1
xT
o1
ot-1
ot
ot+1
oT
P (O | )
T 1
b P a
x1 x1o1
{ x1 ... xT }
t 1
b
xt xt 1 xt 1ot 1
Сложность O (NT), где N – число
возможных вариантов состояний

19. Форвардная процедура

• Метод динамического программирования
• Определим переменную:
i (t ) P(o1...ot , xt i | )
Смысл переменной α: вероятность наблюдений o1, …ot
и при этом оказаться в состоянии i

20. Форвардная процедура

x1
xt-1
xt
xt+1
xT
o1
ot-1
ot
ot+1
oT
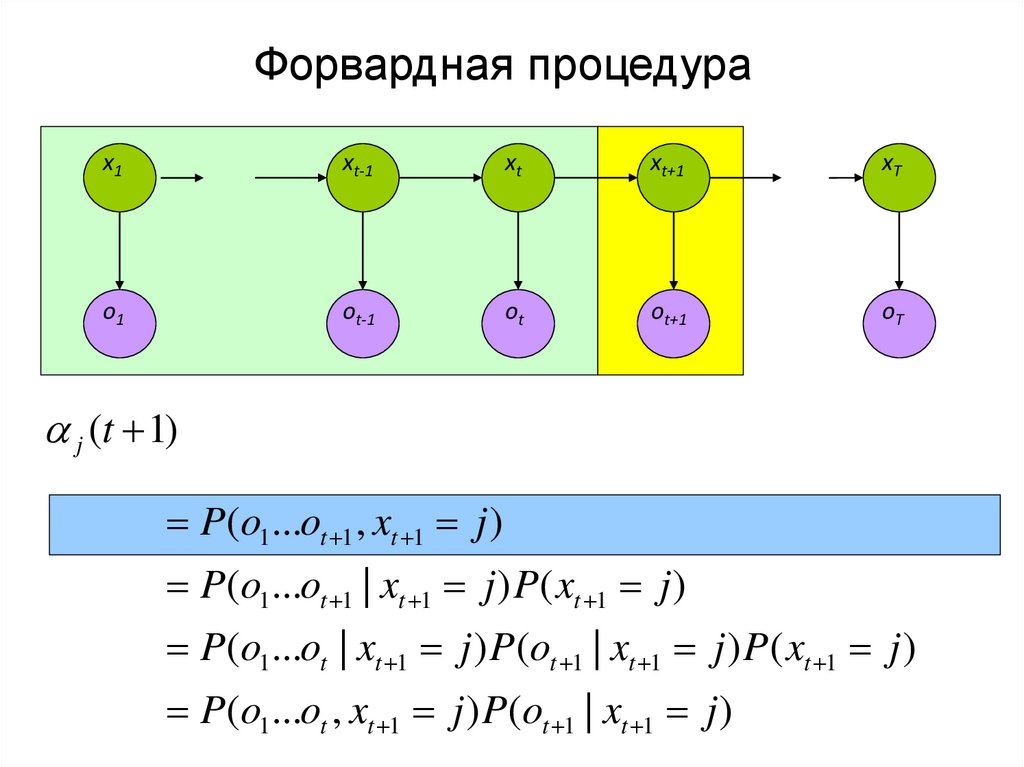
j (t 1)
P(o1...ot 1 , xt 1 j )
P(o1...ot 1 | xt 1 j ) P( xt 1 j )
P(o1...ot | xt 1 j ) P(ot 1 | xt 1 j ) P( xt 1 j )
P(o1...ot , xt 1 j ) P(ot 1 | xt 1 j )

21. Форвардная процедура

x1
xt-1
xt
xt+1
xT
o1
ot-1
ot
ot+1
oT
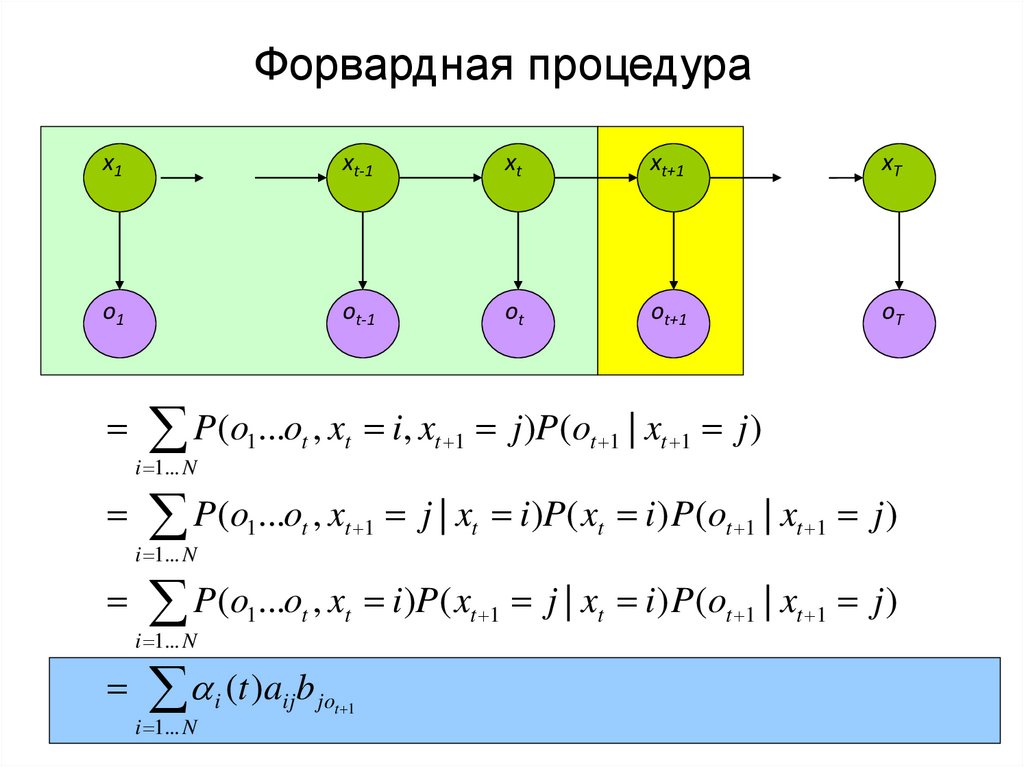
P(o1...ot , xt i, xt 1 j )P (ot 1 | xt 1 j )
i 1... N
P(o1...ot , xt 1 j | xt i )P( xt i ) P (ot 1 | xt 1 j )
i 1... N
P(o1...ot , xt i )P ( xt 1 j | xt i ) P (ot 1 | xt 1 j )
i 1... N
i (t )aijb jot 1
i 1... N

22. Вычисление вероятности последовательности наблюдаемых событий

• Можем эффективно вычислять
• αT(I)=P(o1, o2,…oT, xT=i|μ)
• Как вычислить
• P(o1, o2,…oT |μ)?
• Как вычислить
• P(xT=i|o1, o2,…oT ,μ)?

23. Вычисление вероятности последовательности наблюдаемых событий

• Можем эффективно вычислять
• αT(i)=P(o1, o2,…oT, xT=i|μ)
• Как вычислить
• P(o1, o2,…oT |μ) = Σi αT(i)
• Как вычислить
• P(xT=i|o1, o2,…oT ,μ)= αT(i)/(Σi αT(i))

24. Форвардный алгоритм: пример

25. Форвардный алгоритм

• Найти вероятность
последовательности:
• s r r s r (s- sun, r – rain)

26.

27.

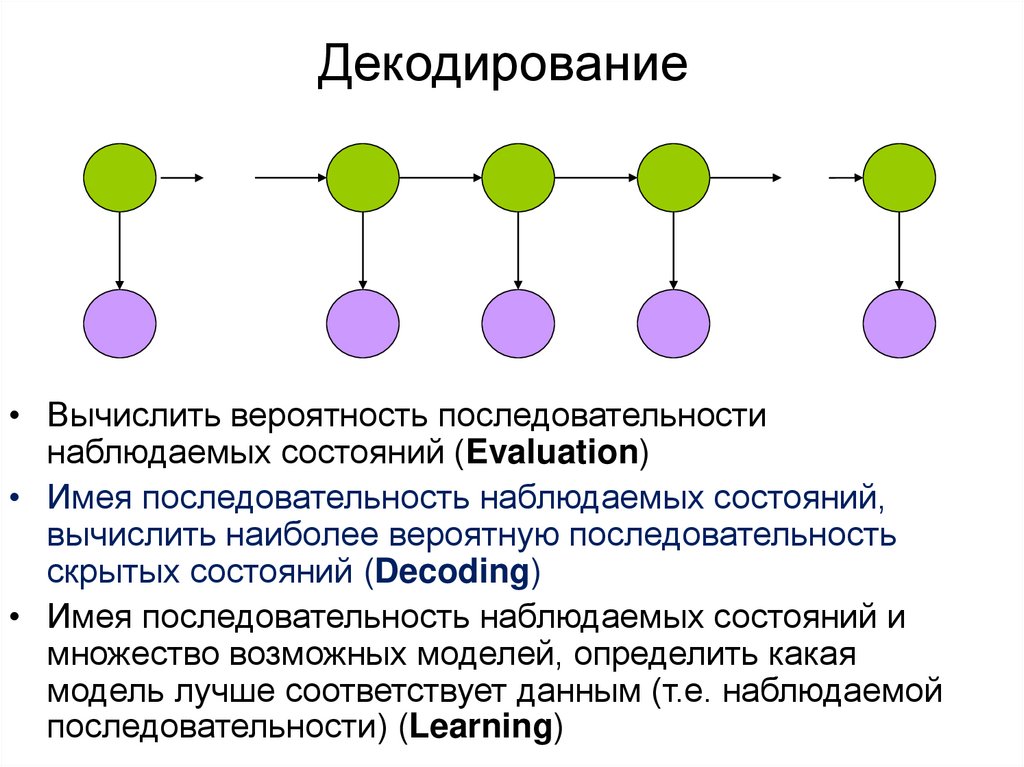
28. Декодирование

• Вычислить вероятность последовательности
наблюдаемых состояний (Evaluation)
• Имея последовательность наблюдаемых состояний,
вычислить наиболее вероятную последовательность
скрытых состояний (Decoding)
• Имея последовательность наблюдаемых состояний и
множество возможных моделей, определить какая
модель лучше соответствует данным (т.е. наблюдаемой
последовательности) (Learning)

29. Декодирование: Best State Sequence

o1
ot-1
ot
ot+1
oT
• Найти множество состояний, которые наилучшим
образом объясняют последовательность видимых
состояний
• Viterbi algorithm
arg max P( X | O)
X

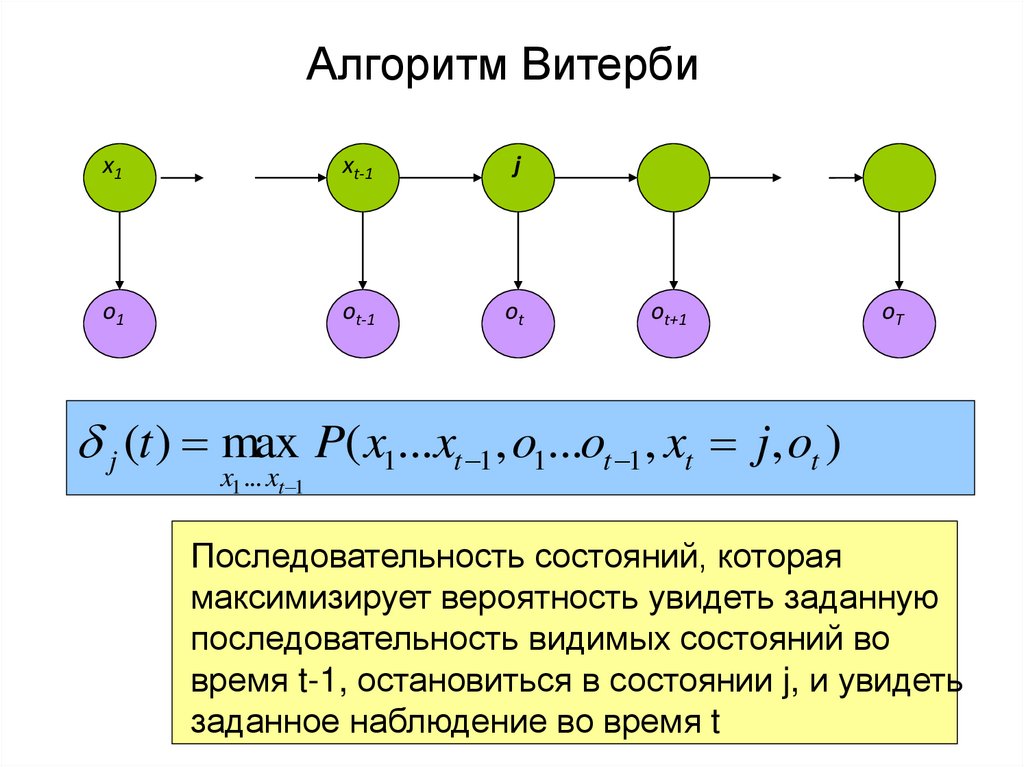
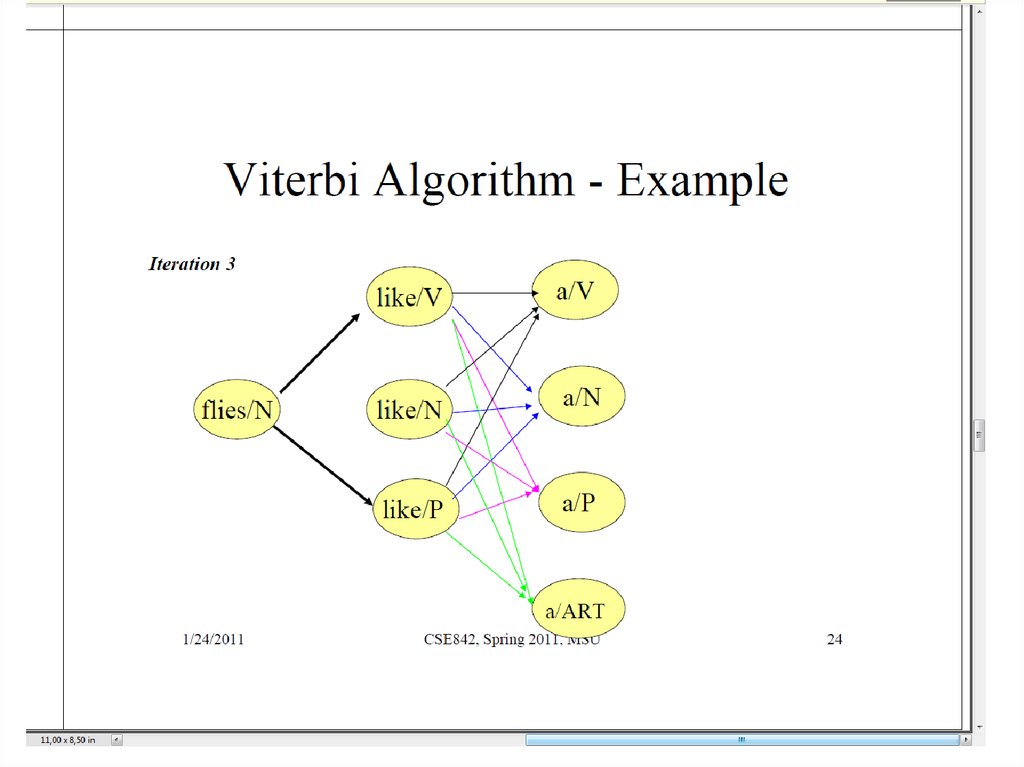
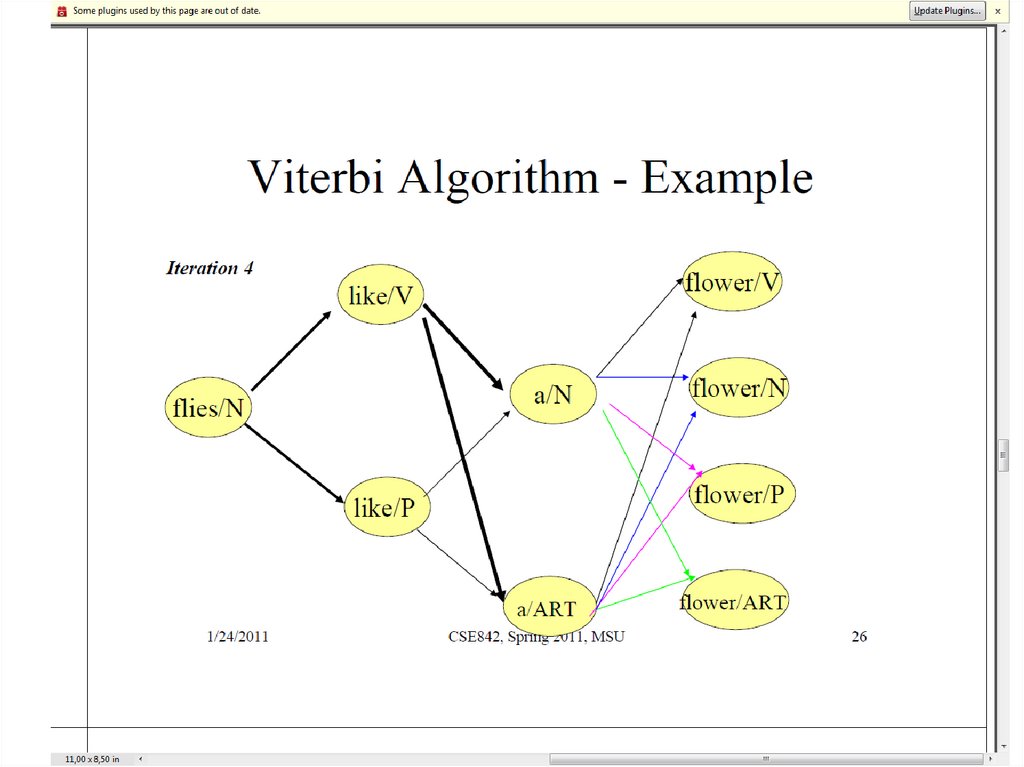
30. Алгоритм Витерби

x1
xt-1
j
o1
ot-1
ot
ot+1
oT
j (t ) max P( x1...xt 1 , o1...ot 1 , xt j, ot )
x1 ... xt 1
Последовательность состояний, которая
максимизирует вероятность увидеть заданную
последовательность видимых состояний во
время t-1, остановиться в состоянии j, и увидеть
заданное наблюдение во время t

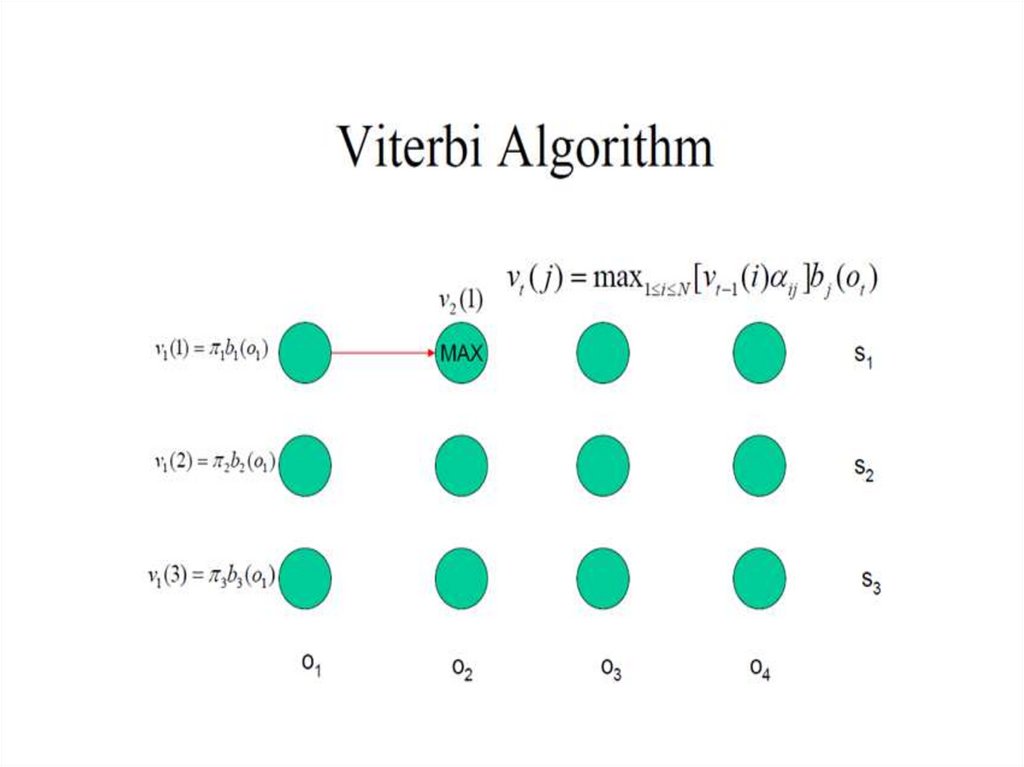
31. Алгоритм Витерби

x1
xt-1
xt
xt+1
o1
ot-1
ot
ot+1
oT
j (t ) max P( x1...xt 1 , o1...ot 1 , xt j, ot )
x1 ... xt 1
j (t 1) max i (t )aijb jo
t 1
i
j (t 1) arg max i (t )aijb jo
i
t 1
Рекурсивное
вычисление

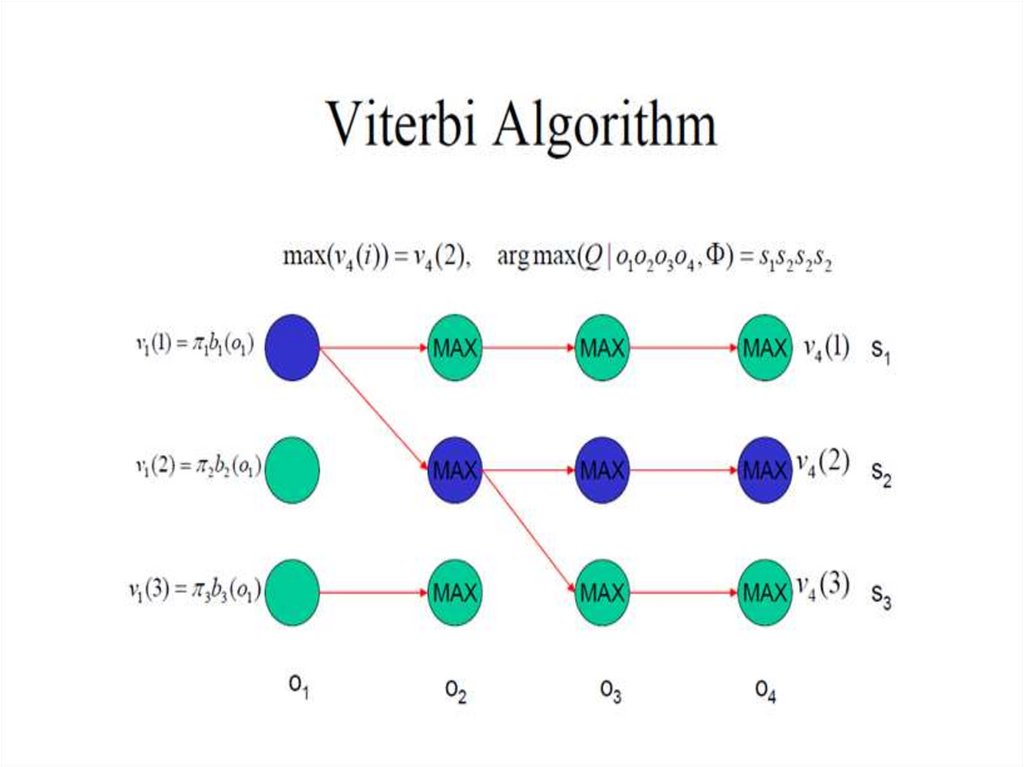
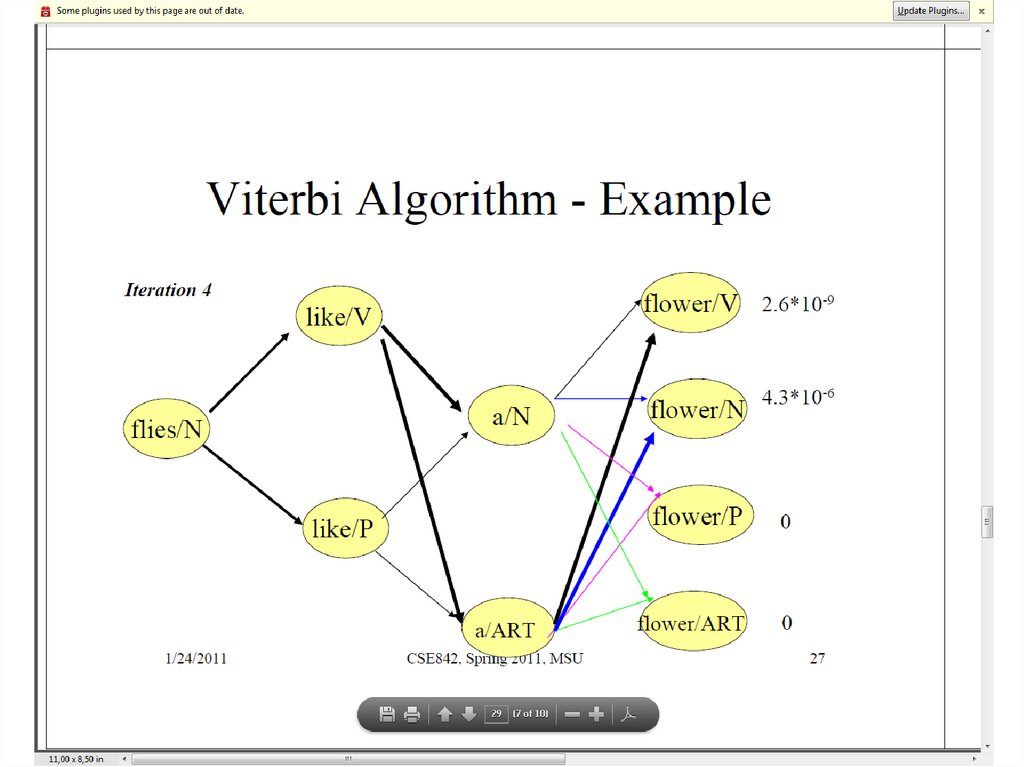
32. Алгоритм Витерби

x1
xt-1
xt
xt+1
xT
o1
ot-1
ot
ot+1
oT
Xˆ T arg max i (T )
i
Xˆ t ^ (t 1)
X t 1
P( Xˆ ) arg max i (T )
i
Вычисляем наиболее
вероятную
последовательность
состояний, двигаясь
назад

33.

34.

35.

36.

37.

38.

39. Тот же пример для алгоритма Витерби

40. Пример: Алгоритм Витерби

41. Пример. Алгоритм Витерби

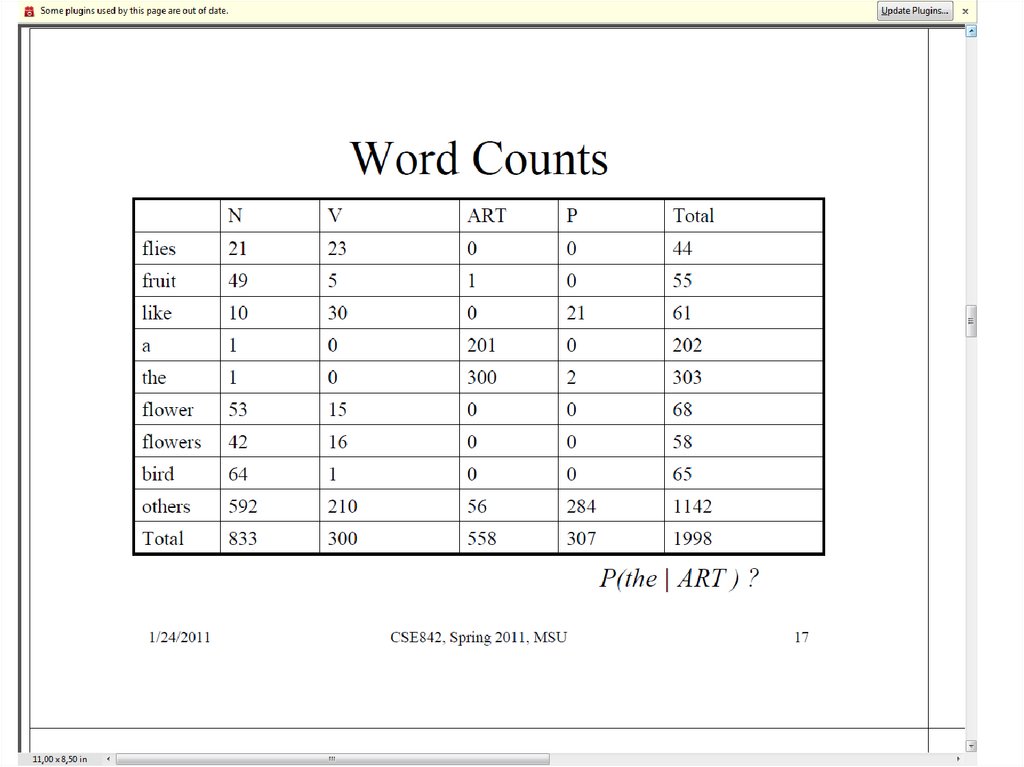
42. Применение HMM к POS-tagging

• POS-tagging – морфологическая разметка
• HMM tagger: выбирает наиболее вероятную
последовательность тегов для каждого
предложения
– Дано предложение W=w1, w2, w3…, wn
- Вычислить наиболее вероятную
последовательность тегов T=t1, t2, …tn, которая
максимизирует
- Argmax P (t1, t2, …tn|w1, w2, …wn)

43. Пример: морфологическая неоднозначность

44. Откуда взять данные?

• Из корпуса с морфологической разметкой
– Русский язык:
• Корпус русского языка
• Открытый корпус (opencorpora.org)
– Английский язык
• Brown corpus
• Penn tree bank

45. Фрагмент морфологической разметки в Национальном корпусе русского языка

Я сидел на барском сиденье, дышал горячим ветром, бившим в лицо, ощущая в
то же время не истребимую никакими сквозняками пыль и легкий запах духов -катафалк с хорошей скоростью мчался по шоссе на юг. (Ю. Трифонов)
<s>Я{я=S,ед,од=им} сидел{сидеть=V,несов=изъяв,прош,ед,муж} на{на=PR}
барском{барский=A=ед,сред,пр} сиденье{сиденье=S,сред,неод=ед,пр},
дышал{дышать=V,несов=изъяв,прош,ед,муж} горячим{горячий=A=ед,муж,твор}
ветром{ветер=S,муж,неод=ед,твор},
бившим{бить=V,несов=прич,прош,ед,муж,твор} в{в=PR}
лицо{лицо=S,сред,неод=ед,вин}, ощущая{ощущать=V=несов,деепр,непрош}
в{в=PR} то{тот=A=ед,сред,вин} же{же=PART} время{время=S,сред,неод=ед,вин}
не{не=PART} истребимую{истребимый=A=ед,жен,вин}
никакими{никакой=A=мн,твор} сквозняками{сквозняк=S,муж,неод=мн,твор}
пыль{пыль=S,жен,неод,ед=вин} и{и=CONJ} легкий{легкий=A=ед,муж,вин,неод}
запах{запах=S,муж,неод=ед,вин}…

46. Данные для примера

47.

48.

49.

50.

51.

52.

53.

54.

55.

56.

57.

58.

59. Лексические вероятности: уточнение

• Мы считали p(w|t)
• Но
– Слово могло отсутствовать в корпусе или отсутствовать
в заданной части речи
– Не учитывается информация из морфологического
словаря
– Удобнее оценить p (t Iw)

60. Лексические вероятности

p(t | w) p( w)
p( w | t )
p(t | w)
p(t )
p(t )
• p(t) – априорная вероятность метки
• p(t|w) – вероятность метки для данного слова
• Можно положить
p(t | w)
c(t , w)
c( w)
• Где с () – количество вхождений
• Как учесть словарь?

61. Словарь и лексические вероятности

• Можно считать, что все словарные метки слова w входят в
корпус раз (например, =0.5)
• Тогда получим:
c(t , w)
p(t | w)
c( w) | T ( w) |
• где T(w) – это количество тегов для w
• Для новых несловарных слов p(t|w) считается на основе
совокупности признаков (машинное обучение)

62. Анализ статистических алгоритмов снятия морфологической омонимии в русском языке

Егор Лакомкин
Иван Пузыревский
Дарья Рыжова
(2013)

63. Разрешение морфологической неоднозначности в текстах на английском языке

• Методы:
Как правило, статистические
алгоритмы на основе марковских
моделей
• Точность: ~96%

64. Особенности английского языка

• Бедная морфология
морфологическая разметка фактически сводится к
POS-теггингу
• Фиксированный порядок слов
можно опираться только на локальный контекст
слова (ближайших соседей) без учёта дальних
зависимостей (т.е. достаточно марковских моделей
первого порядка)

65. Задача исследования:

Проверить экспериментально,
применимы ли статистические
алгоритмы, основанные на
марковских моделях, к задаче
морфологической дизамбигуации
текстов на русском языке

66. Алгоритмы

• Набор скрытых величин Y (состояний модели =
наборов грамматических тегов); составляют
марковскую цепь первого порядка
• Набор наблюдаемых величин X (наблюдений) ~
словоформ
Словоформы заменяем на 3-буквенные
окончания:
– Сокращаем количество наблюдаемых состояний
– Практически не теряем полезную информацию
(поскольку в РЯ почти вся морфологическая
информация сосредоточена в окончании)

67. HMM

• Обучение:
Сбор статистик по корпусу:
– P(yi|yj) – матрица переходов
– P(xk|yi) – вероятности наблюдений
прил
сущ
глаг
-ные
-чки
-ают

68. Задача алгоритмов:

Вычисление наиболее вероятной
последовательности скрытых величин

69. Деление выборки на обучающую и тестирующую:

• Кросс-валидация (5 фолдов):
– Деление выборки на 5 частей:
4 обучающие + 1 тестирующая
– 5 серий подсчётов
– Усреднение результата

70. Оценка качества

• Определение верхней и нижней границы:
– Верхняя граница: процент случаев, когда среди гипотез
Mystem’а есть правильная;
– Нижняя: «частотная снималка» (слову приписывается
наиболее частотный вариант разбора, без учёта контекста)
• Качество работы алгоритма (= точность):
Сравнение с «золотым стандартом» - с эталонным разбором
НКРЯ:
– общая точность
– точность по знакомым словам
– точность по незнакомым словам
• Не учитывались:
– Инициалы, аббревиатуры, цифры;
– Сложные слова с дефисом (ср. бело-кремовый)

71. Результаты

Части речи
Теги (род, число, падеж и
др.)
Общ.
Зн.
Незн.
Общ.
Зн.
Незн.
Нижн.гр.
.8590
.8586
.8885
.6817
.6836
.5525
HMM
.9482
.9489
.8996
.8873
.8909
.6550
.9895
.9081
.9741
.7017
Верхн.гр.

72. Выводы работы

• POS-теггинг – на приличном уровне,
• Разрешение неоднозначности по
расширенным тегам – довольно низкий
уровень точности. Случаи, особенно часто
разбираемые ошибочно:
– Местоимения
– Имена собственные
– Субстантивация прилагательных
– Омонимия падежных форм (номинатив vs.
аккузатив)

73. Проблемы HMM

• Метки рассматриваются как единое целое,
невозможно извлечь отдельные признаки
– В русском языке: тег – это сущ. в род. падеже ед.
числа
• Ограниченный просмотр состояний – обычно
биграммы
• Не учитываются дистантные зависимости
– Договор о разоружении сторон был подписан
– Договор – именительный или винительный падеж
• Состояние не зависит от соседних слов
– Обмануть друга vs. соврать другу

74. Как можно изменить процесс расчета переходов между состояниями?

• HMM: учитываются два фактора в простой
комбинации
• Для определения вероятности переходов
между состояниями нужно: учитывать
значительно больше факторов
• Когда нужна комбинация факторов ->
машинное обучение

75. Задание