Похожие презентации:
Ромб та його властивості
1.
2.
• працювати над засвоєннямучнями змісту означень,
властивостей та ознак ромба.
• формувати вміння
відтворювати вивчені
твердження;
• застосовувати властивості,
ознаки ромба до розв'язування
типових задач.
3.
Варіант 11. Чи є прямокутником
паралелограм, один із
кутів якого прямий?
2. Чи правильно, що кожен
прямокутник є
паралелограмом?
3. Діагоналі прямокутника
АЕКМ перетинаються в
точці О. Відрізок АО
дорівнює 3 дм. Знайдіть
довжину діагоналі ЕМ.
4. Діагоналі чотирикутника
рівні. Чи обов'язково
цей чотирикутник є
прямокутником?
Варіант 2
1. Чи обов'язково
чотирикутник з прямим
кутом є прямокутником?
2. Чи правильно, що кожен
паралелограм є
прямокутником?
3. Діагоналі паралелограма
мають довжину 3 дм і 5
дм. Чи цей паралелограм є
прямокутником?
4. Сума довжин діагоналей
прямокутника дорівнює
13 м. Знайдіть довжину
кожної діагоналі.
Умова
завдань
не
записується,
відповідь має бути короткою, але
змістовною (тобто у відповіді має бути
аргументація
—
відповідне
геометричне твердження).
4.
Варіант 11. Так
2. Так
3. 6 дм
4. Ні
Варіант 2
1. Ні
2. Ні
3. Ні
4. 6,5 м
5.
• Яких помилок припустилися під часзображення паралелограма (рис. 1)?
• У трикутнику АВС <А = <С, ВС = 15 см. Яку
зі сторін трикутника можна знайти за
цими даними? AB
• У трикутнику АВС <А = <В. До якої
сторони проведена медіана буде AB
висотою і бісектрисою?
• ВМ — медіана рівнобедреного
трикутника, проведена до основи АС,
<С =40°. Знайдіть <АВМ.
50°
6.
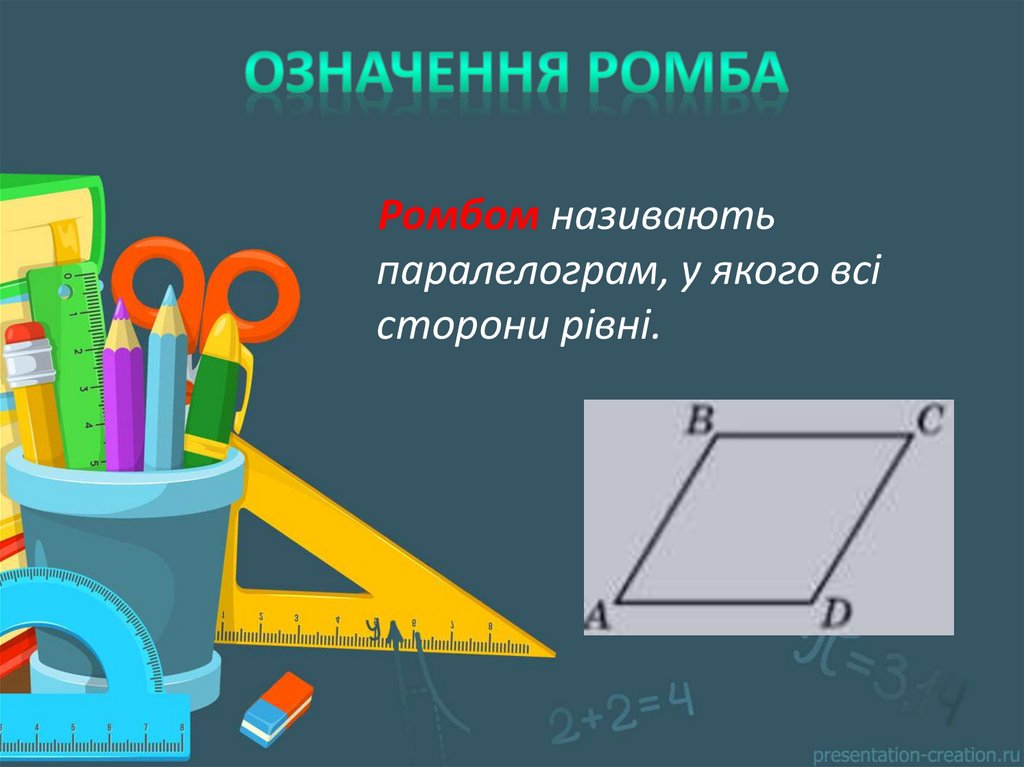
Ромбом називаютьпаралелограм, у якого всі
сторони рівні.
7.
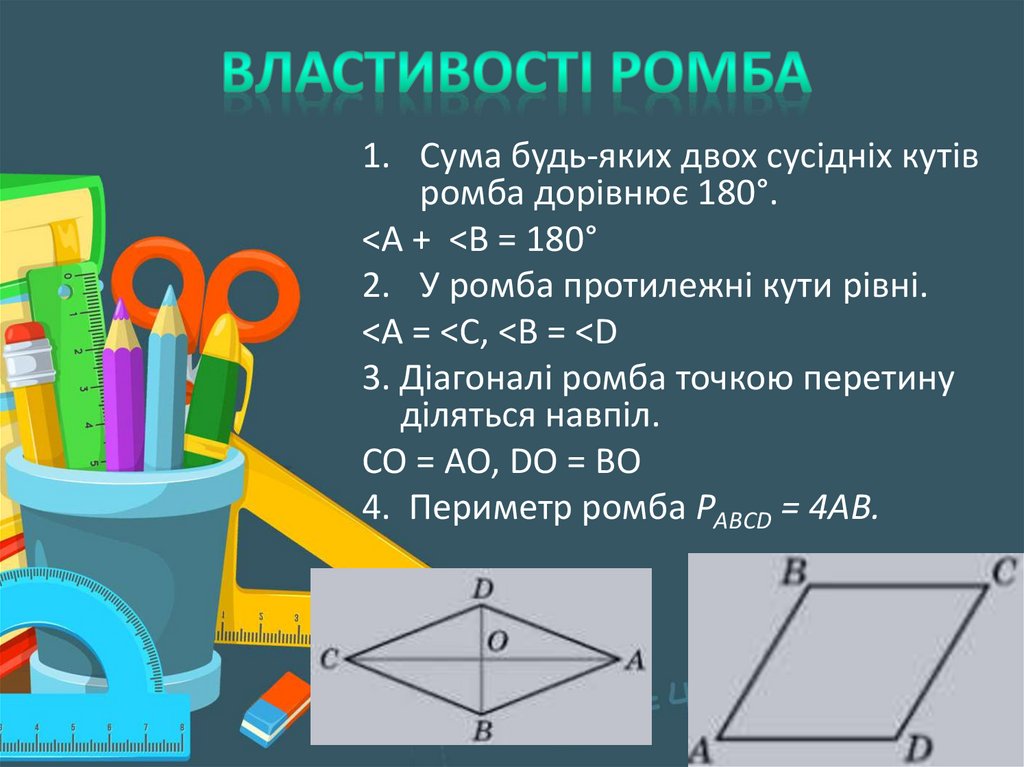
1. Сума будь-яких двох сусідніх кутівромба дорівнює 180°.
<A + <B = 180°
2. У ромба протилежні кути рівні.
<A = <C, <B = <D
3. Діагоналі ромба точкою перетину
діляться навпіл.
CO = AO, DO = BO
4. Периметр ромба РАВСD = 4АВ.
8.
5. Діагоналі ромба взаємноперпендикулярні і ділять його
кути навпіл.
<DAO = < BAO, <DCO = <BCO,
<CBO = <ABO, <ADO = <CDO
9.
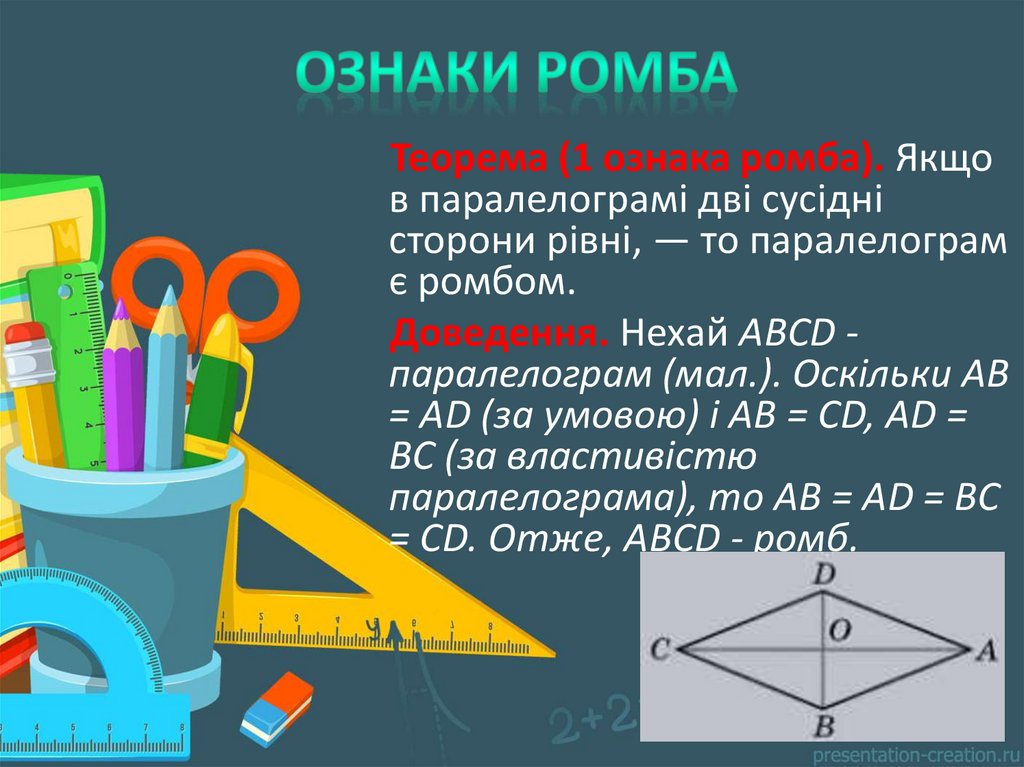
Теорема (1 ознака ромба). Якщов паралелограмі дві сусідні
сторони рівні, — то паралелограм
є ромбом.
Доведення. Нехай АВСD паралелограм (мал.). Оскільки АВ
= АD (за умовою) і АВ = СD, АD =
ВС (за властивістю
паралелограма), то АВ = АD = ВС
= СD. Отже, АВСD - ромб.
10.
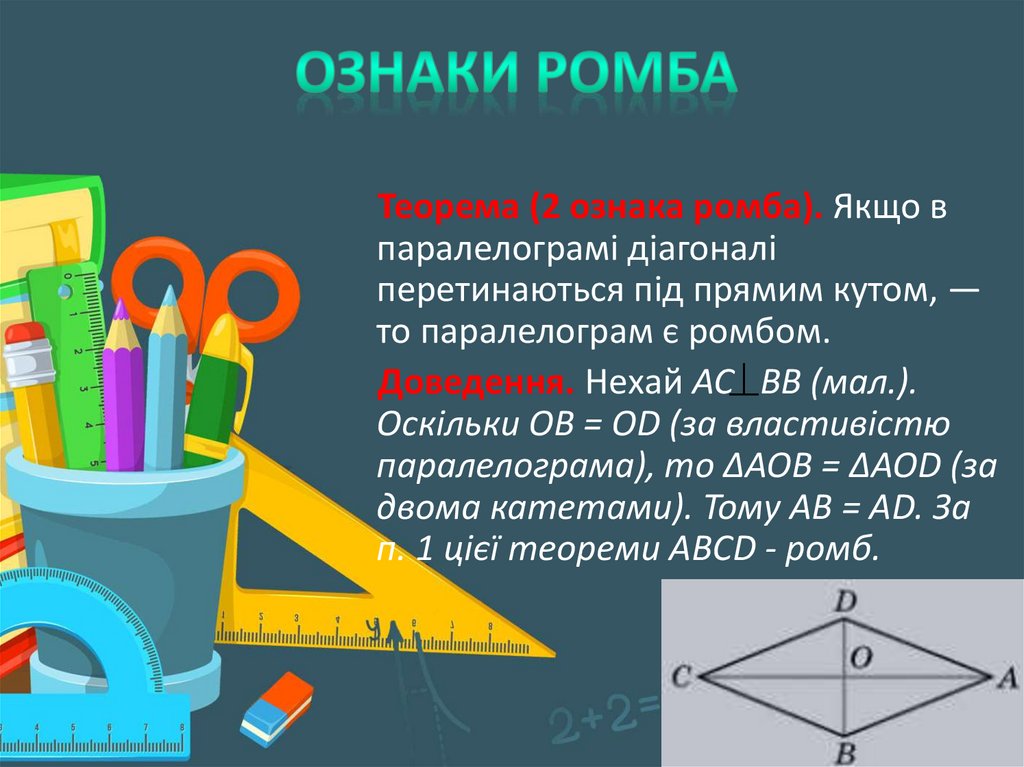
Теорема (2 ознака ромба). Якщо впаралелограмі діагоналі
перетинаються під прямим кутом, —
то паралелограм є ромбом.
Доведення. Нехай АС ВВ (мал.).
Оскільки ОВ = ОD (за властивістю
паралелограма), то ∆АОВ = ∆АОD (за
двома катетами). Тому АВ = АD. За
п. 1 цієї теореми АВСD - ромб.
11.
Теорема (3 ознака ромба). Якщо впаралелограмі діагональ ділить навпіл
кути паралелограма, — то
паралелограм є ромбом.
Доведення. Діагональ DВ ділить
навпіл кут D паралелограма АВСD,
тобто <АDВ = <ВDС (за умовою).
Оскільки паралельні прямі АВ і DС
перетнули січною DВ, то <АВD = <ВDС
(як внутрішні різносторонні). Отже,
<АDВ = <АВD. Тому, за ознакою
рівнобедреного трикутника, ∆АВD рівнобедрений і АD = АВ. За п. 1 цієї
теореми АВСD - ромб.
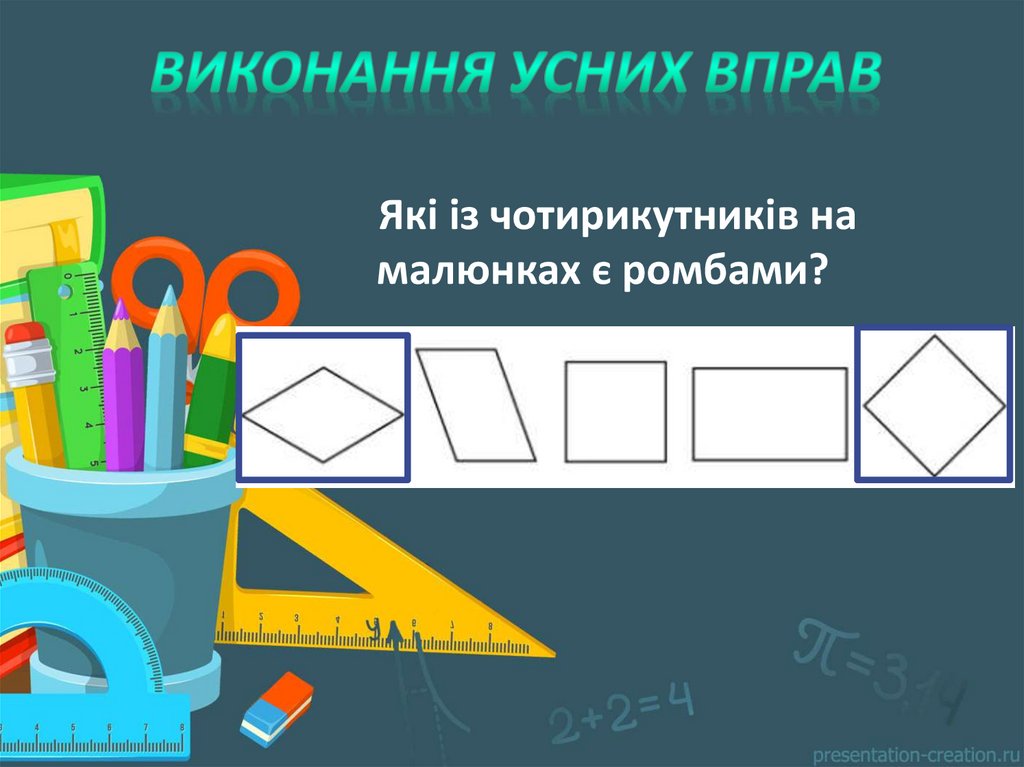
12.
Які із чотирикутників намалюнках є ромбами?
13.
Назвіть види паралелограмів, уяких:
а) усі кути рівні;
б) усі сторони рівні;
в) діагоналі рівні;
г) діагоналі перпендикулярні.
14.
Діагоналі квадрата ABCDперетинаються в точці О.
Назвіть усі рівні трикутники, які
утворюються при перетині
діагоналей. Визначте її вид.
15.
Знайдіть кути ромба, якщоодин із них на 120° більший за
інший.
<A = <C = 30°;
<B = <D = 150°
16.
Сума довжин трьох сторінромба дорівнює 15 см.
Знайдіть його периметр.
20см
17.
№138. У ромбі АВСD з вершинитупого кута В проведено
висоти ВМ і ВN. Доведіть, що
ВМ = BN.
18.
§ 4, ст. 26 – 27, №19.
• Геометрія 8 кл. О.О. Старова,І.С.Маркова. - видавнича
група "Основа". 2020 р.
• Геометрія підруч. для 8 кл.
загальноосвіт. навч. закл./ О.
С. Істер. - Київ : Генеза, 2016
р.














 Математика
Математика








