Похожие презентации:
Волны в упругой среде. Тема 2
1.
Тема 2. Волны в упругой средеОсновные вопросы темы:
2.1. Образование волн. Принцип Гюйгенса
2.2. Уравнение бегущей волны
2.3. Волновое уравнение
2.4. Скорость волны
2.5. Энергия упругой волны
2.6. Звуковые волны
2.7.Эффект Доплера
2.
2.1. Образование волн. Принцип Гюйгенса.3.
Процессраспространения
колебаний
в
пространстве, сопровождающийся переносом
энергии, называется волной.
4.
Волна называется поперечной, если направление колебаний частиц среды перпендикулярно направлению распространения волны.Волна называется продольной, если направление колебаний частиц среды совпадает с направлением распространения волны.
5.
6.
7.
Геометрическое место точек, до которых доходятколебания к моменту времени t, называется фронтом
волны (волновым фронтом).
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью.
8.
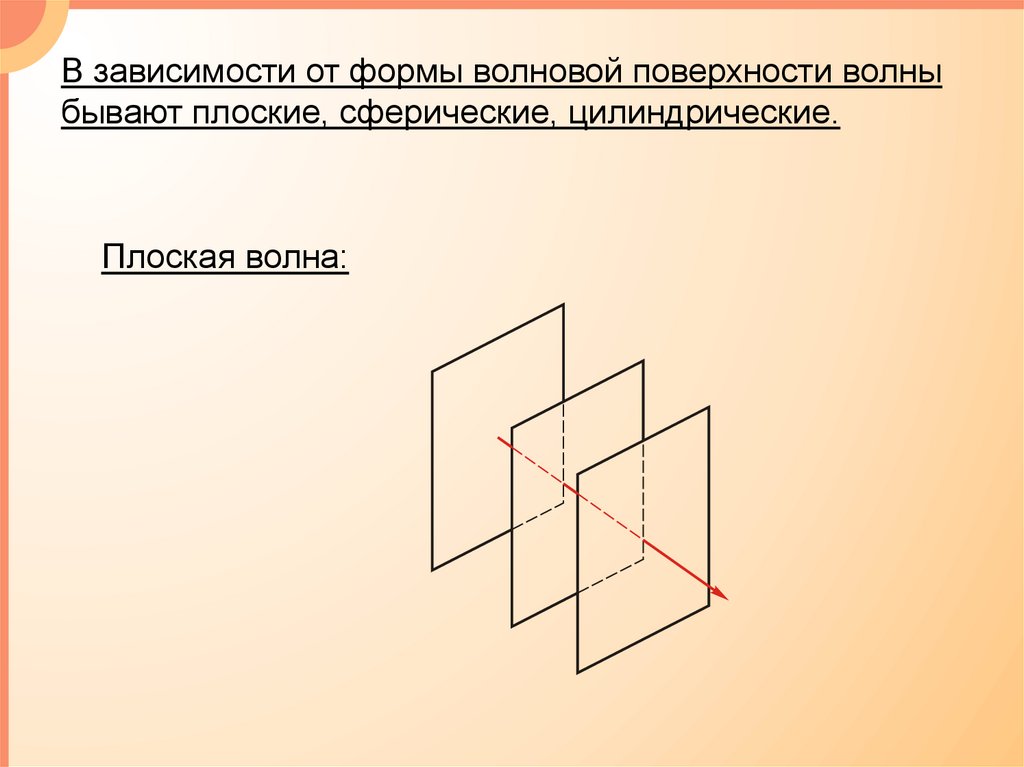
В зависимости от формы волновой поверхности волныбывают плоские, сферические, цилиндрические.
Плоская волна:
9.
Цилиндрическая волна:Сферическая волна:
10.
Принцип Гюйгенса:Каждая точка среды, до которой дошло колебание,
становится источником вторичных волн, а огибающая
этих вторичных волн дает положение волнового фронта в
последующий момент времени.
11.
2.2. Уравнение бегущей волны.Волны, которые переносят в пространстве энергию,
называются бегущими.
Уравнением волны называется выражение, которое
определяет зависимость смещения колеблющейся
частицы от координат ее положения равновесия x, y, z и
времени t:
x , y , z, t
(2.1)
12.
Волна называется гармонической, если соответствующие ейколебания частиц среды являются гармоническими.
1. Уравнение плоской гармонической волны,
распространяющейся вдоль оси
Уравнение колебаний точек, лежащих в плоскости х=0, имеют вид:
0, t A cos t
(2.2)
13.
Чтобы колебанию достигнуть точки с координатой Х, потребуетсявремя
x v
Уравнение колебаний в точке с координатой Х:
x, t A cos t
x , t A cos t x v
A cos t x
v
(2.3)
14.
Зависимость смещения ξ частиц среды от расстояния хот источника колебаний (при t=const)
15.
Длина волны – это расстояние, проходимое волной завремя, равное периоду колебания.
Длина волны - это расстояние между двумя гребнями
или двумя впадинами.
Расстояние между ближайшими точками,
колеблющимися в одинаковой фазе, называется длиной
волны ( ).
16.
Величина k=ω/v называется волновым числом, а векторk=k·n, где n – единичный вектор нормали к волновой
поверхности, называется волновым вектором.
к
2
Уравнение плоской гармонической волны, распространяющейся вдоль
оси Х:
x, t A cos t kx
(2.5)
Уравнение плоской гармонической волны, распространяющейся в произвольном
направлении:
r , t A cos t k r
(2.6)
17.
2. Уравнение сферической волныA
r , t cos t k r
r
(2.7)
18.
2.3. Волновое уравнение.Волновое уравнение – это дифференциальное уравнение
в частных производных, решением которого является
уравнение волны.
x, t A cos t kx
Уравнение плоской волны является решением
волнового уравнения:
2 1 2
2 2
2
x
v t
(2.8)
19.
2.4. Скорость упругих волн.Фазовая скорость - скорость перемещения точек
поверхности, соответствующей любому фиксированному
значению фазы волны.
Зафиксируем значение фазы волны:
x
(t ) const
V
Продифференцируем по времени:
dx
V
dt
V-фазовая скорость
20.
2.5. Энергия упругой волны.Уравнение плоской гармонической волны, распространяющейся вдоль оси х:
A cos t kx
(2.9)
w A sin t kx
2
2
2
(2.10)
Энергия упругой волны пропорциональна квадрату амплитуды
Энергию волны характеризуют средней по времени
плотностью потока энергии или интенсивностью волны
Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется
потоком энергии через эту поверхность.
dW
Ф
(2.11)
dt
21.
Плотностью потока энергии называется вектор, численноравный потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно к направлению,
в котором переносится энергия, и направленный в направлении распространения волны.
dФ
dW
j
n
n
dS
dS dt
(2.12)
[ Вт / м ]
2
Выразим энергию, переносимую волной, через объемную плотность
энергии w:
22.
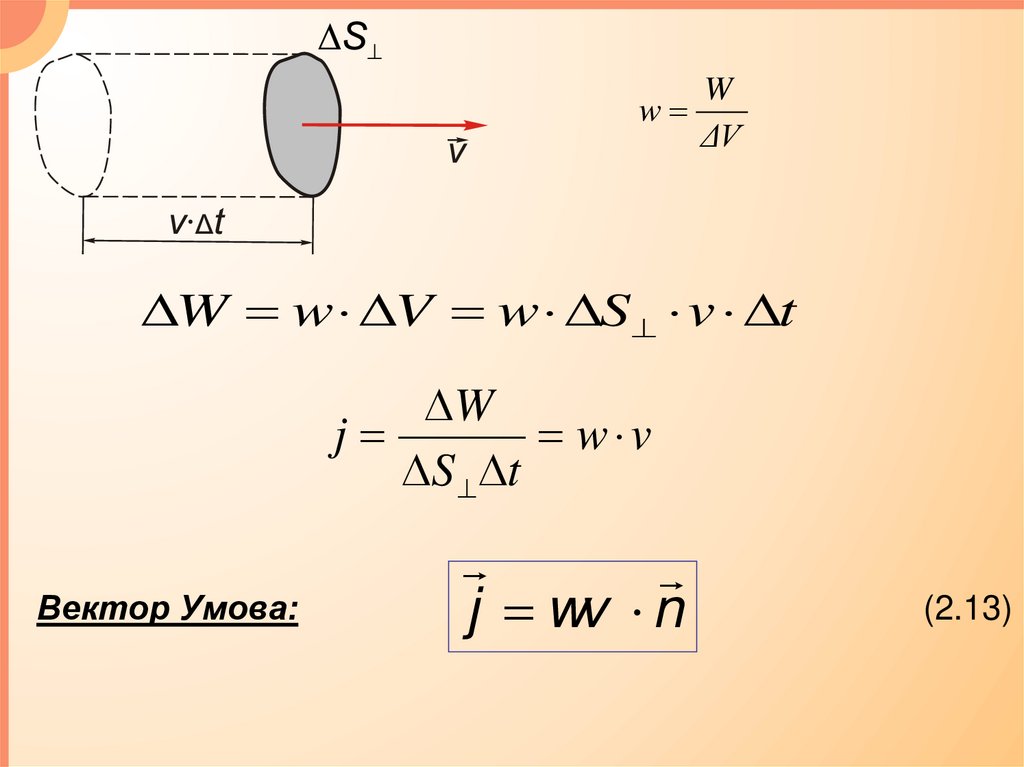
Ww
ΔV
W w V w S v t
W
j
w v
S t
Вектор Умова:
j wv n
(2.13)
23.
2.6. Звуковые волны.Звуковые волны (звук) – это упругие волны в
диапазоне частот от 16 Гц до 20 кГц, воспринимаемые
ухом человека.
ν < 16 Гц – инфразвук
ν> 10 9 Гц - гиперзвук
ν > 20 кГц - ультразвук
Любой реальный звук есть сумма многих гармонических колебаний
с разными частотами и амплитудами.
Распределение интенсивности звуковой волны по
частотам называется акустическим спектром.
24.
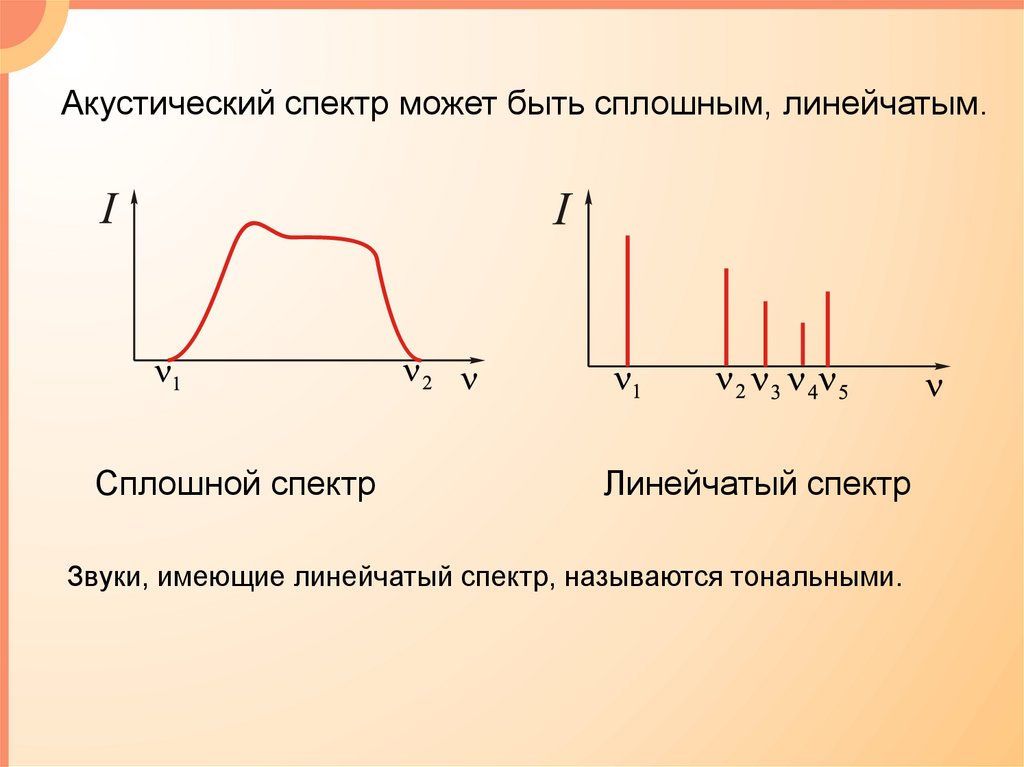
Акустический спектр может быть сплошным, линейчатым.Сплошной спектр
Линейчатый спектр
Звуки, имеющие линейчатый спектр, называются тональными.
25.
Звук человек различает по высоте, тембру и громкости.Высота звука определяется частотой ν.
Тембр звука определяется характером акустического
спектра колебаний.
Громкость звука – субъективная характеристика звука,
связанная с его интенсивностью.
26.
Интенсивность(сила) звука - среднее по временизначение плотности потока энергии, переносимой
звуковой волной, т.е. среднее значение вектора Умова:
1
2 2 Вт
I j w V A V 2
2
м
ρ - плотность среды, А-амплитуда,
ω-круговая частота, V-фазовая скорость волны
(2.14)
27.
Для каждой частоты колебаний существует наименьшая(порог слышимости) I0, и наибольшая I (болевой порог
чувствительности)I интенсивности звука, вызывающие
звуковое восприятие.
Порог слышимости:
0,5 5,0 кГц
Iпор 10
12
Вт м
2
Порог болевого ощущения:
Iбол ≈ 1 ÷ 10 Вт/м2
Уровень интенсивности звука:
I
LБел lg
I0
I
LдБ 10 lg
I0
(2.15)
28.
20 дБ = 100 раз29.
ЗвукУровень громкости,
L, дБ
Тиканье часов
20
Тихий шепот
30
Нормальный разговор
60
Громкая речь
70
Крик
80
Оркестр фортиссимо
100
Шум самолетного мотора
на расстоянии 5 м
120
на расстоянии 3 м
130
30.
2.7. Эффект Доплера.Эффект Доплера заключается в изменении частоты
волн, воспринимаемой наблюдателем, при движении
наблюдателя и источника волн относительно друг друга.
v –фазовая скорость волны, u –скорость движения источника,
u´ - скорость движения приемника, ν –частота колебаний источника
31.
Период колебаний источника:Длина волны (источник неподвижен):
1
V
T
Длина волны для наблюдателя:
vT
vT uT
1. Приемник неподвижен:
v
v
T v u
32.
2. Приемник движется навстречу источнику:v u - скорость импульсов относительно приемника
v u
v u
T v u
v u
v u x
v ux
33.
Реверберация – процесс постепенного затухания звукав закрытых помещениях после выключения его источника.
Время реверберации – время, в течении которого
интенсивность звука в помещениях ослабляется в миллион
раз, а его уровень - на 60дБ.
Помещение обладает хорошей акустикой, если время
реверберации составляет 0,5 – 1.5 секунд.






























 Физика
Физика








