Сопротивление материалов. Экспресс – тесты по основным разделам курса

1.

Вспомним «Сопротивление материалов»
(вопросы и ответы для проверки уровня знаний)
Экспресс – тесты по основным разделам курса
Составители:
А.В. Терновой
М.С. Луковникова

2.

Содержание
Раздел 1. Введение в курс
Раздел 2. Напряженное и
деформируемое состояние в точке
Раздел 3. Растяжение и сжатие
Раздел 4. Сдвиг. Кручение
Раздел 5. Плоский прямой изгиб
Раздел 6. Сложное сопротивление
(комбинированные виды нагружения)
Раздел 7. Сопротивление динамическим
и периодически меняющимся во
времени нагрузкам
Раздел 8. Статически неопределимые
системы
Раздел 9. Устойчивость сжатых
стержней
Список рекомендуемой литературы
2

3.

Раздел 1. Введение в курс.
1. Отсутствие отказов, связанных с разрушением или
недопустимыми деформациями элементов
конструкций называют…
жесткостью
прочностью
устойчивостью
прочностной надежностью
2. Если не учитывается конкретная структура материала
(зернистая, кристаллическая и др.), и считается, что
материал непрерывно заполняет весь объем элемента
конструкции, то материал обладает свойством…
изотропности
анизотропности
сплошности
однородности и изотропности
3. Принцип утверждающий, что в точках тела, достаточно
удаленных от места приложения сил, внутренние
силы не зависят от характера распределения внешних
сил (и зависят лишь от статического эквивалента
последних) называется…
принципом начальных размеров
принципом независимости действия сил
принципом Сен-Венана
принципом суперпозиции
4. Принцип, утверждающий, что результат действия
системы сил равен сумме результатов действий сил
каждой силы в отдельности, называется…
5. Тело, длина которого l существенно превышает
конкретные размеры поперечного сечения (ширины и
высоты) b и h, называется…
принципом Сен-Венана
принципом независимости действия сил
все утверждения верны
принципом начальных размеров
стержнем (брусом)
пластинкой
оболочкой
массивом (пространственным телом)
3

4.

Раздел 1.
6. Свойство твердых тел возвращаться к своим
первоначальным размерам после прекращения действия
внешних сил называется…
прочностью
устойчивостью
выносливостью
упругостью
7. Способность твердого тела (конструкции) сохранять свое
состояние (равновесия или движения) при внешних
воздействиях называется…
устойчивостью
выносливостью
прочностью
жесткостью
8. Метод, позволяющий определить внутренние усилия в
сечении стержня, называется…
методом начальных параметров
методом независимости действия сил
методом сил
методом сечений
9. Величины, служащие мерой механического действия
одного материального тела на другое, называются…
внутренними силовыми факторами
напряжениями
внутренними силами
внешними силами (нагрузками)
10. Материал, у которого механические свойства во всех
направления одинаковы, называется…
изотропным
линейно-упругим
анизотропным
однородным
4

5.

Раздел 1.
11. Чугун и сталь – материалы…
12. примером анизотропного материала является…
вязкоупругие
неоднородные
анизотропные
изотропные
чугун
древесина
бетон
сталь
13. Образец из малоуглеродгой стали, предназначенный для
испытаний на растяжение, имеет вид…
14. Перемещение точки в процессе деформации тела из
одного положения в положение, бесконечно близкое к
нему, называется…
15. Изменение размеров или формы реального тела,
подверженного действию внешних сил, называется…
угловым перемещение
относительной деформацией
деформированным состоянием
линейным перемещением
пластичностью
упругостью
перемещением
деформацией
5

6.

Раздел 1.
16. Проекция главного вектора R внутренних сил на
ось (X или Y), лежащую в плоскости сечения,
называется…
поперечной силой Qx (или Qy)
продольной силой N
касательным напряжением
напряженным состоянием
17. Момент внутренних сил, действующих в
поперечном сечении стержня, относительно оси
X (или Y), лежащей в плоскости сечения,
называется…
изгибающим моментом Mx (или My)
моментом силы относительно оси
крутящим моментом Mx
главным моментом
18. Изменение первоначальной длины стержня l
обозначаемое Δl, называется…
19. Отношение абсолютного удлинения
(укорочения) Δl стержня к первоначальной
длине l называется…
20. Отношение абсолютного сдвига ΔS к расстоянию
между сдвигающимися
плоскостями a
называется…
абсолютным удлинением (укорочением)
деформацией
изменением формы стержня
относительной линейной деформацией
средней относительной линейной деформацией εср
изменением формы стержня
относительным изменением объема
угловой деформацией
относительным сдвигом
модулем Юнга
модулем сдвига
законом Гука при сдвиге
6

7.

Раздел 1.
21. Принцип независимости действия сил
(суперпозиции) применим в сопротивлении
материалов…
22. К объемным силам относится…
- при определении потенциальной энергии деформации
- при определении перемещений и внутренних сил,
если деформации малы и следуют закону Гука
- при определении работы внутренних сил
- при определении работы внешних сил
погонная нагрузка
собственный вес тела
сосредоточенная сила
нагрузка, распределенная по поверхности
23. Интегральная связь между поперечной силой Qх в
поперечном сечении бруса
площадью А и
касательными
напряжениями имеет вид…
Qx zxdA
Qx zy dA
Qx zx ydA
Qx zx xdA
A
A
A
A
24. Абсолютное удлинение (укорочение) имеет
размерность…
м
м2
м3
1/м
СОДЕРЖАНИЕ
7

8.

Раздел 2. Напряженное и деформированное состояния в точке.
1. Компонент вектора полного напряжения p,
действующего в некоторой точке сечения тела,
определяемый проекцией вектора p на плоскость
сечения называется…
2. Вектор полного напряжения на данной площадке p
раскладывают на составляющие (на
нормаль к площадке и на плоскость
этой площадки). Эти составляющие
называют…
3. Под напряженным состоянием в какойлибо точке деформируемого тела
следует понимать
поперечной силой
напряженным состоянием
нормальным напряжением σ
касательным напряжением τ
напряженным состоянием в точке
внутренними силовыми факторами
тензором напряжений
нормальными и касательными напряжениями
совокупность нормальных и касательных напряжений в
поперечном сечении стержня
совокупность нормальных и касательных напряжений в
любом сечении стержня
совокупность нормальных и касательных напряжений на
любых трех элементарных плоскостях, походящих
через эту точку
совокупность нормальных и касательных напряжений,
действующих по множеству элементарных площадок,
проходящих через эту точку
8

9.

Раздел 2.
4. Главные площадки это…
три взаимно-перпендикулярные плоскости, проходящие через данную
точку деформируемого тела, на которых касательные напряжения
экстремальны
три взаимно-перпендикулярные плоскости, проходящие через данную
точку деформируемого тела, на которых отсутствуют нормальные
напряжения
три взаимно-перпендикулярные плоскости, проходящие через данную
точку деформируемого тела, на которых нормальные и
касательные компоненты напряжений экстремальны
-три взаимно-перпендикулярные плоскости, проходящие через
данную точку деформируемого тела, на которых отсутствуют
касательные напряжения
5. Компоненты тензора деформаций εx, εy, εz, Ζxy,
Ζyz, Ζzx, представленные в виде функций
координат X,Y,Z, определяют…
6. Относительные линейные деформации ε1, ε2,
ε3 (ε1 = εmax, ε3 = εmin) называются…
деформированное состояние в точке
деформированное состояние тела
напряженное состояние в точке
напряженное состояние тела
предельными деформациями
экстремальными деформациями
максимальными деформациями
главными деформациями
9

10.

Раздел 2.
7. Выберите неверное утверждение.
Тензор напряжений…
полностью характеризует (определяет) напряженное
состояние в точке деформируемого тела
позволяет вычислить величину и направление главных
напряжений в точке деформируемого тела
позволяет установить вид (тип) напряженного состояния в
точке деформируемого тела
совокупность нормальных и касательных напряжений в
поперечном сечении стержня
8. На одной грани элемента действуют
нормальные напряжения. Такое
напряженное состояние называется…
объемным (трехосным)
чистым сдвигом
линейным (одноосным)
плоским (двухосным)
9. Напряженное состояние, возникающее в
точке С, имеет вид…
10

11.

Раздел 2.
10. Условия прочности по теории наибольших
относительных линейных деформаций имеет
вид…
11. При сложном напряженном
состоянии для оценки прочности
хрупких и пластичных (вязких)
материалов рекомендуется
использовать…
σ1 – σ3 < [σ]
σ1 < [σ], σ3 < [σ]
σ1 – kσ3 < [σ]
σ1 – μσ2 + σ3 < [σ]
энергетическую теорию прочности
теорию наибольших относительных линейных деформаций
теорию прочности Мора
теорию наибольших касательных напряжений
12. При сложном напряженном состоянии эквивалентное
напряжение по теории прочности Мора (σэкв. = σ1 – kσ3,
материал серый чугун k = 0,2) равно…
13. При сложном напряженном состоянии эквивалентное
напряжение по теории наибольших относительных линейных
деформаций (σэкв. = σ1 – μσ2 + σ3,
материал сталь, μ = 0,3) равно…
1,66σ
1,2σ
2,2σ
1,8σ
1,3σ
1,6σ
σ
0
11

12.

Раздел 2.
14. При сложном напряженном состоянии, показанном на рисунке,
приведенное (эквивалентное) напряжение по теории наибольших
касательных напряжений σэкв = σ1 – σ3 равно…
15. По двум граням элементарного параллелепипеда действуют
нормальные напряжения σ. Одинаковую по
модулю деформацию ε имеют ребра…
0
2σ
–σ
σ
I, II, III
I, II
I, III
II, III
16. Относительная линейная деформация ε ребра 1
равна нулю в напряженном состоянии…
17. Удельная потенциальная энергия изменения формы
uф = ((1+μ)/6Е)[( σ1 – σ2)2 + (σ2 – σ3)2 + (σ3 – σ1)2],
μ – коэффициент Пуассона, Е – модуль упругости
равна нулю в напряженном состоянии… (в каком из
трех случаев А, Б или В?)
12

13.

Раздел 2.
18.
max
min
x y
2
1
2
4
2
x
y
1 5
2
1 5
2
2
xy
Для заданного напряженного состояния
максимальное из главных напряжений равно…
19. В окрестности точки К консольной балки
напряженное состояние…
20.
Условие прочности по
энергетической гипотезе
имеет вид…
21.
1
1 2 3
E
1
q1 2 3 1
E
1
q1 3 1 2
E
q1
Элементарный объем выделен главными площадками.
Линейная деформация в направлении С – С равна…
2 5
2
2 5
2
- линейное (одноосное растяжение)
- «нулевое» - нормальные и касательные
напряжения отсутствуют
- линейное (одноосное сжатие)
- плоское (чистый сдвиг)
3
2
3
2
1
Å
1 2
Å
1
Å
1 2
Å
СОДЕРЖАНИЕ
13

14.

Раздел 3. Растяжение и сжатие.
1. Диаграмма растяжения малоуглеродистой стали имеет
вид…
2. При линейном напряженном состоянии закон Гука
выражается зависимостью…
3. В растянутом стержне главные
площадки совпадают с…
d
a
c
b
l
l
E
G
E
G
2 1
поперечными и продольными сечениями
с наклонными (под углом π/4 к продольной оси) сечениями
только с поперечными сечениями
только с продольными сечениями
4. Если предел пропорциональности материала и
соответствующая ему деформация равны σП = 100МПа,
εП = 0.0014, тогда величина модуля упругости равна…
5. На рисунке показана диаграмма растяжения стального
образца диаметром 0.01м. масштаб нагрузки – 1 деления –
0.007Мн.
Тогда предел текучести
материала равен…
83110 МПа
71429 МПа
65822 МПа
55782 МПа
268 МПа
310 МПа
200 МПа
166 МПа
14

15.

Раздел 3.
6. Чугунный образец диаметром 0.015м разрушился при
F = 0.12 Мн.
Тогда величина предела прочности равна…
527 МПа
679 МПа
750 МПа
815 МПа
7. Для стержня, схема которого изображена на рисунке,
нормальное усилие N в сечении 1-1 будет…
растягивающим и сжимающим
сжимающим
равна нулю
растягивающим
8. Для стержня, схема которого изображена на рисунке,
деформации, возникающие в сечении 1-1 будут…
растягивающими
сжимающими
растягивающими и сжимающими
равны нулю
15

16.

Раздел 3.
9. Для стержня, схема которого изображена на рисунке,
деформации, возникающие в сечении 1-1 будут…
сжимающими
растягивающими
растягивающими и сжимающими
равны нулю
10. Для стержня, схема которого изображена на
рисунке,нормальные напряжения, действующие в сечении
1-1 будут…
растягивающими и сжимающими
растягивающими
сжимающими
равны нулю
11. Для стержня, схема которого изображена на
рисунке,деформации, возникающие в сечении 1-1 будут…
равны нулю
сжимающими
растягивающими
растягивающими и сжимающими
16

17.

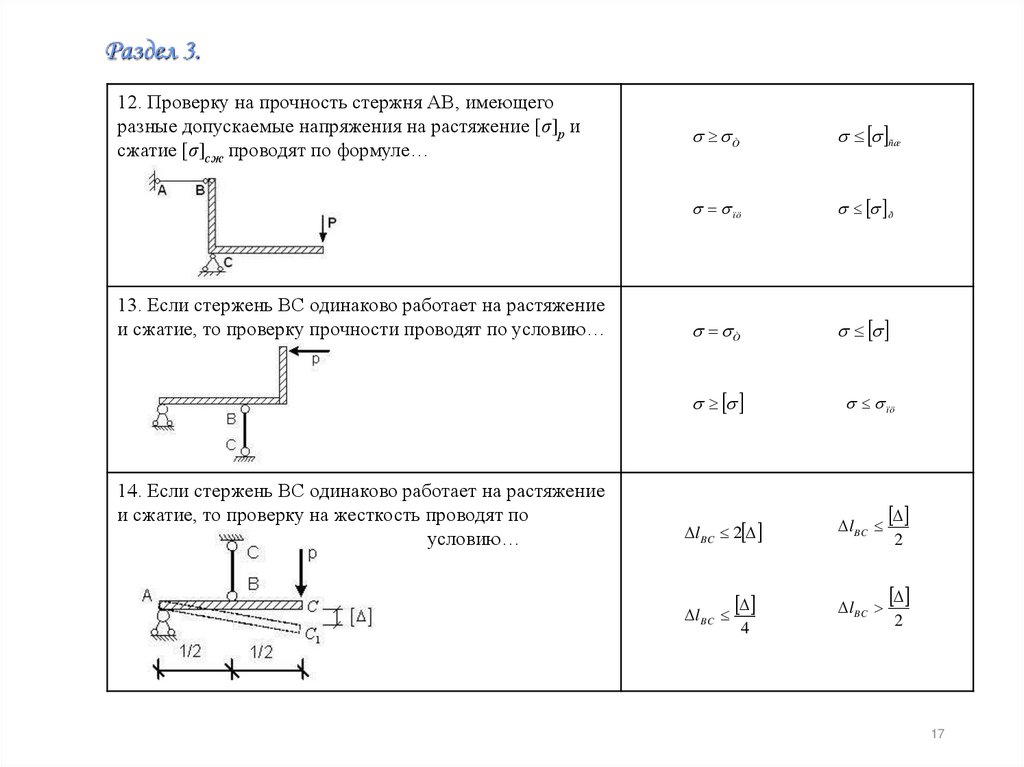
Раздел 3.
12. Проверку на прочность стержня АВ, имеющего
разные допускаемые напряжения на растяжение [σ]р и
сжатие [σ]сж проводят по формуле…
13. Если стержень ВС одинаково работает на растяжение
и сжатие, то проверку прочности проводят по условию…
14. Если стержень ВС одинаково работает на растяжение
и сжатие, то проверку на жесткость проводят по
условию…
Ò
ñæ
ïö
ð
Ò
ïö
l BC 2
l BC
l BC
l BC
4
2
2
17

18.

Раздел 3.
15. Для стержня изображенного на рисунке,
эпюра нормальных сил N будет иметь вид…
16. Растяжению образца из пластичного материала
без площадки текучести соответствует диаграмма,
приведенная на рисунке…
17. В результате испытания цилиндрического 70мм с площадью
поперечного сечения 100мм2 была получена диаграмма, представленная на
рисунке. Площадь шейки в месте разрыва образца составила 50мм2.
Относительное остаточное сужение после разрыва равно…
14%
16%
20%
50%
18. Жесткий брус, нагруженный сосредоточенным моментом М,
поддерживается в горизонтальном положении стальным
стержнем площадью поперечного сечения А.
Ì
2à À
Ì
2à À
Ì
À
Ì à
À
Условие прочности стержня имеет вид…
СОДЕРЖАНИЕ
18

19.

Раздел 4. Сдвиг, кручение.
1. На срез (на сдвиг) рассчитывается
соединение, показанное на рисунке…
2. Закон Гука при чистом сдвиге выражается
формулой…
Å
3. Закон Гука при чистом сдвиге ( G)
действует на участке
диаграммы…
G
Ì êð L
L
GI ð
NL
EA
3–4
2–3
4–5
0–1
4. Изменение касательных напряжений вдоль
радиуса поперечного сечения круглого
стержня при кручении соответствует
рисунку…
19

20.

Раздел 4.
5. В процессе кручения длина стержня L…
не изменяется
уменьшается
увеличивается
сначала увеличивается, потом уменьшается
6. Касательное напряжение в центре тяжести
поперечного сечения (точка К) равно…
7. В окрестности точки К скручиваемого
стержня
напряженное
состояние…
Md
2J p
2M
Wp
0
M
Wp
плоское (чистый сдвиг)
«нулевое»-нормальные и касательные напряжения отсутствуют
8. Если к тонкостенной трубе приложен
скручивающий момент М, то напряженным
состоянием для элементарного объема «abcd»
будет…
линейное (одноосное растяжение)
линейное (одноосное сжатие)
линейное напряженное состояние
сложное напряженное состояние
объемное напряженное состояние
чистый сдвиг
20

21.

Раздел 4.
9. Пусть к тонкостенной трубке приложен
скручивающий момент М.
Тогда деформация элемента
элемента стенки трубы
показана на рисунке…
10. Стержень скручивается. Максимальные касательные
напряжения действуют…
11. Условие жесткости стержня при кручении имеет вид…
12. Взаимный угол поворота концевых сечений равен «φ».
Жесткость поперечного сечения на кручение равна…
в точке D
в точках B и C
в точке А
во всех точках на поверхности стержня
max max
max
max
max
GI p
ML
3
GI p
ML
2
GI p
ML
GI p
2ML
21

22.

Раздел 4.
13. Условие прочности для стержня имеет вид…
14. Известен взаимный угол поворота сечений А и В.
Модуль сдвига
материала образца
равен…
M
Wp
2M
Wp
3M
Wp
3Md
Ip
G
15. В скручиваемом стержне максимальные касательные
напряжения действуют…
16. Если [τ] – допускаемое касательное напряжение, то из
расчета на прочность, скручивающий момент…
E
G
ML
A B I P
G
E
2 1
G
2 ML
A B I P
на III участке
на I участке
на II участке
на I и II участках
M
4
d 3
M
32
d 3
M
d 3
M
32
d 3
16
22

23.

Раздел 4.
17. Если [τ] – допускаемое касательное напряжение, то из расчета
на прочность диаметр вала…
18. [Θ] – допускаемый относительный угол закручивания.
Условие жесткости для вала…
19. Пусть GIp – жесткость поперечного сечения на кручение.
Тогда максимальный относительный угол закручивания равен…
20. Угол поворота сечения С равен…
d 3
16M
d 3
32 M
d 4
16M
d 3
M
2M
GI p
M
2GI p
4M
GI p
M
GI p
2M
GI p
M
4GI p
4M
GI p
M
GI p
2 ML
GI p
ML
2GI p
ML
GI p
ML
3GI p
23

24.

Раздел 4.
21. Пусть [φ]с – допускаемый угол поворота С, GIp –
жесткость поперечного сечения на кручение.
M
M
GI p c
M
2L
GI p c
3GI p c
L
M GI p c
L
Тогда допускаемая величина М удовлетворяет
неравенству…
22. Для определения перемещений при кручении
применяется интеграл…
M кp M x
EJ
23. При чистом сдвиге…
kQp Q
GA dz
dz
x
M p( кр ) M
GJ p
Np N
( кр )
dz
EA dz
σ1 = 0, σ2 = – σ, σ3 = – σ
σ1 = σ, , σ3 = – σ
σ1 = σ, σ2 = σ, σ3 = 0
σ1 = σ, σ2 = σ, σ3 = σ
24

25.

Раздел 4.
24. Если максимальные касательные напряжения от крутящего
момента в поперечном сечении трубы с наружным диаметром
100мм и внутренним – 80мм составляют 60МПа, то касательные
напряжения в точках у внутренней поверхности сечения трубы
равны…
150МПа
75МПа
48МПа
24МПа
25.
8
êÍ
; d 2ñì
ñì 2
6π кН · см
5π кН · см
Из расчета на прочность
максимальное допустимое
значение момента М равно…
26. Условие жесткости вала постоянного сечения (см. рисунок)
при допускаемом относительном угле закручивания [Θ]
(рад/м) имеет вид…
4π кН · см
3π кН · см
Ì
GJ p
5ÌL
GJ p
2Ì
GJ p
3ÌL
GJ p
СОДЕРЖАНИЕ
25

26.

Раздел 5. Плоский прямой изгиб.
1. В сечении 1-1 имеют место внутренние
силовые факторы…
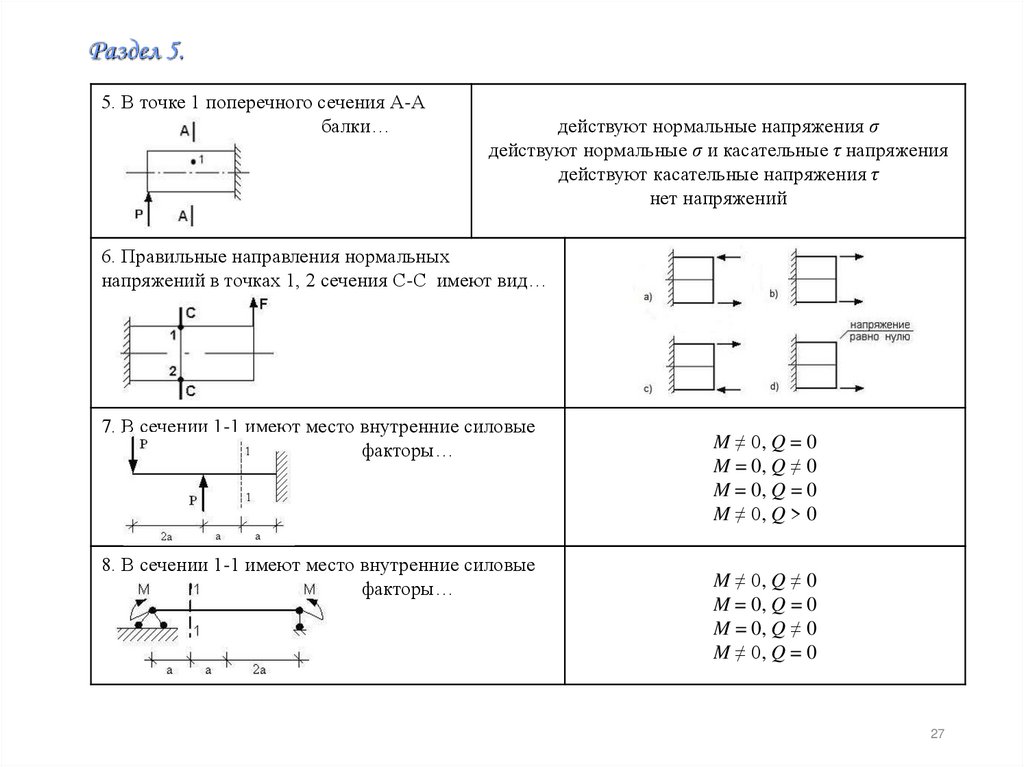
2. В точке 1 поперечного сечения А-А
балки…
3. В сечении 1-1 имеют место внутренние
силовые факторы…
4. В точке 1 поперечного сечения А-А
балки…
M ≠ 0, Q = 0
M = 0, Q = 0
M = 0, Q ≠ 0
M ≠ 0, Q ≠ 0
действуют нормальные σ и касательные τ напряжения
действуют нормальные напряжения σ
нет напряжений
действуют касательные напряжения τ
M ≠ 0, Q ≠ 0
M = 0, Q = 0
M ≠ 0, Q = 0
M = 0, Q ≠ 0
действуют нормальные напряжения σ
действуют касательные напряжения τ
действуют нормальные σ и касательные τ напряжения
нет напряжений
26

27.

Раздел 5.
5. В точке 1 поперечного сечения А-А
балки…
действуют нормальные напряжения σ
действуют нормальные σ и касательные τ напряжения
действуют касательные напряжения τ
нет напряжений
6. Правильные направления нормальных
напряжений в точках 1, 2 сечения С-С имеют вид…
7. В сечении 1-1 имеют место внутренние силовые
факторы…
8. В сечении 1-1 имеют место внутренние силовые
факторы…
M ≠ 0, Q = 0
M = 0, Q ≠ 0
M = 0, Q = 0
M ≠ 0, Q > 0
M ≠ 0, Q ≠ 0
M = 0, Q = 0
M = 0, Q ≠ 0
M ≠ 0, Q = 0
27

28.

Раздел 5.
9. φ – угол поворота, v – прогиб. Сечение 1-1 имеет
перемещения…
нет перемещений
v
φ
φиv
10.Правильные направления касательных напряжений
в поперечном сечении
С-С имеют вид…
11. В сечении 1-1 имеют место внутренние силовые
факторы…
12. φ – угол поворота, v – прогиб. Сечение 1-1 имеет
перемещения…
M ≠ 0, Q = 0
M = 0, Q ≠ 0
M ≠ 0, Q ≠ 0
M = 0, Q = 0
нет перемещений
φиv
φ
v
28

29.

Раздел 5.
13. φ – угол поворота, v – прогиб. Сечение 1-1 имеет
перемещения…
v
φиv
нет перемещений
φ
14. φ – угол поворота, v – прогиб. Сечение 1-1 имеет
перемещения…
15. Нормальные напряжения при плоском изгибе
определяются по формуле…
φиv
v
φ
нет перемещений
16. Максимальные нормальные напряжения действуют
в точках…
Mzy Myy
Iz
Iy
Mzy
Iz
N
A
N Mzy
A
Iz
8, 5
1, 2, 7, 6
10, 3, 8, 5
9, 4
29

30.

Раздел 5.
17. Тип (вид) напряженного состояния в
окрестности точки К консольной балки…
18. Вид (тип) напряженного состояния в
окрестности точки К…
19. Тип (вид) напряженного состояния в
окрестности точки К…
20. В точке 1 поперечного сечения А-А
балки…
плоское (двухосное растяжение – сжатие)
линейное (одноосное растяжение)
плоское (чистый сдвиг)
линейное (одноосное сжатие)
линейное - сжатие
плоское - чистый сдвиг
линейное - растяжение
«нулевое» - напряжения отсутствуют
плоское (чистый сдвиг)
линейное (растяжение)
линейное (сжатие)
«нулевое» - напряжения отсутствуют
действуют касательные напряжения τ
действуют нормальные σ и касательные τ напряжения
нет напряжений
действуют нормальные напряжения σ
30

31.

Раздел 5.
21. В поперечном сечении балки при изгибе могут возникать внутренние
силовые факторы: Q – поперечная сила, М – изгибающий момент.
В сечении 1-1 балки, представленной
на рисунке…
22. При нагружении балки круглого поперечного сечения диаметром d в
сечении возникают изгибающие моменты Мx и поперечная сила Qy.
Нормальное и касательное напряжения в точке А
сечения соответственно равны…
23. Шарнирно опертая балка нагружена сосредоточенным
моментом М. Осевой момент сопротивления поперечного сечения
балки равен W.
Условие прочности для данной
балки имеет вид…
есть М и Q
есть только Q
нет М и Q
есть только М
σ = 0; τ = 0
σ = 0; τ = τmax
σ = σmax; τ = τmax
σ = σmax; τ = 0
M
W
Ml
2W
M
2W
Ml
W
24. На рисунке показана схема нагружения балки.
Форма деформированной оси балки имеет вид…
СОДЕРЖАНИЕ
31

32.

Раздел 6. Сложное сопротивление (комбинированные виды нагружения).
1. На схеме изображенной на рисунке, наиболее
опасной точкой является…
2. Опасными точками в сечении А-А являются точки…
3. Для нагруженного стержня вид сложного
сопротивления называется…
4. Для нагруженного стержня вид сложного
сопротивления называется…
точка 4
точка 3
точка 2
точка 1
3и4
1и3
1и2
2и4
изгибом с кручением
косым изгибом
общим случаем сложного сопротивления
внецентренным сжатием
изгибом с кручением
общим случаем сложного сопротивления
косым изгибом
внецентренным растяжением
32

33.

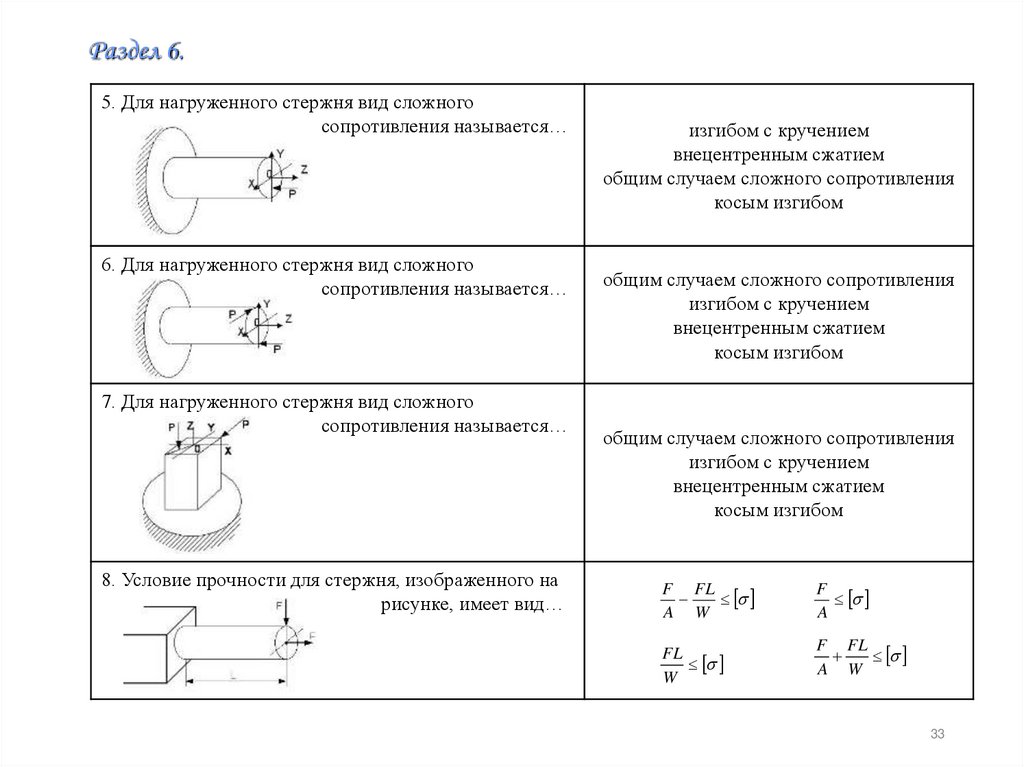
Раздел 6.
5. Для нагруженного стержня вид сложного
сопротивления называется…
6. Для нагруженного стержня вид сложного
сопротивления называется…
7. Для нагруженного стержня вид сложного
сопротивления называется…
8. Условие прочности для стержня, изображенного на
рисунке, имеет вид…
изгибом с кручением
внецентренным сжатием
общим случаем сложного сопротивления
косым изгибом
общим случаем сложного сопротивления
изгибом с кручением
внецентренным сжатием
косым изгибом
общим случаем сложного сопротивления
изгибом с кручением
внецентренным сжатием
косым изгибом
F FL
A W
F
A
FL
W
F FL
A W
33

34.

Раздел 6.
9. Максимальное нормальное напряжение действует…
в точке 1
в точке 3
в точке 2
в точке 4
10. Опасными точками являются точки…
BиD
BиC
Aи C
Aи D
11. Опасными точками являются точки…
BиD
Aи C
Aи B
DиC
12. В сечении А-А нейтральной осью является линия…
3–3
совпадающая с осью X
2–2
1–1
34

35.

Раздел 6.
13. Нейтральной осью поперечного сечения является
линия…
1–1
совпадающая с осью X
2–2
совпадающая с осью Y
14. На схеме, изображенной на рисунке, наиболее
опасной точкой является…
точка 4
точка 2
точка 3
точка 1
15. Напряженное состояние, возникающее в точке С,
имеет вид…
16. Нормальное напряжение в точке С, определяется по
формуле
N Mz y M yz
A
Iz
Iy
равно…
F
2t 2
15.5 2
F
t
31 2
F
t
F
2t 2
35

36.

Раздел 6.
17. Условия прочности для стержня имеет вид…
18. Вид напряженного состояния в точке С…
F FL
A W
F
A
FL
W
F FL
A W
плоское напряженное состояние
линейное напряженное состояние (растяжение)
линейное напряженное состояние (сжатие)
объемное напряженное состояние
19. Вид напряженного состояния в опасных
точках при кручении с изгибом стержня круглого
поперечного сечения…
линейное напряженное состояние нулевое
напряженное состояние
плоское напряженное состояние
плоское напряженное состояние (чистый сдвиг)
36

37.

Раздел 6.
20. В случае сложного сопротивления стержня
для определения напряжений и деформаций в
пределах применимости закона Гука
используются…
21.
При известных Р, α, b, с
нормальное напряжение
в точке В поперечного
сечения стержня равно…
22.
Если известны величины Р,d,
то эквивалентное напряжение в
точке В в поперечном сечении
стержня по теории прочности
наибольших касательных
напряжений равно…
- метод сил
- принцип независимости действия сил
- принцип Сен-Венана
- допущение о равномерности распределения
напряжений по сечению
3Ðlsin
b3
3Ðl cos
b3
8Ð
d 2
20
3Ðlsin
2b 3
Ðlsin
2b 3
8Ð
10
d 2
8Ð
8
d 2
0
23.
При известных величинах Р,d
нормальное напряжение в
точке о поперечного сечения
стержня равно…
Ð
d 2
4Ð
d 2
Ð
4 d 2
2Ð
d 2
СОДЕРЖАНИЕ
37

38.

Раздел 7. Сопротивление динамическим и периодически меняющимся во времени нагрузкам.
1. Тело движется ускоренно. Для того
чтобы динамическую задачу свести к
статической, к телу необходимо
приложить…
силы инерции и активные силы
активные и реактивные силы
активные силы, реактивные силы, силы инерции
реактивные силы и силы инерции
2. Принцип Даламбера формируется
следующим образом…
силы инерции, приложенные к телу, движущемуся
ускорению, образуют систему сил, которая удовлетворяет
уравнениям равновесия статики
если к активным и реактивным силам, действующим на тело,
которое движется ускоренно, добавить силы инерции, то
полученная система сил будет самоуравновешенной и
должна удовлетворять уравнениям равновесия статики
система активных и реактивных сил, действующих на тело,
которое движется ускоренно, образуют самоуравновешенную
систему сил
результат действия системы сил равен сумме результатов
действий каждой силы в отдельности
38

39.

Раздел 7.
3. Тело весом Р равномерно вращается в вертикальной
плоскости вокруг оси, проходящей через точку О. Напряжения
в проволоке будут максимальными, когда тело находится в
положении…
2
1
4
3
4. Ломаный стержень АВС вращается с постоянной угловой
скоростью. Максимальное
нормальной напряжение на участке
АВ равно…
аn – нормальное ускорение груза,
m – масса груза, Р – вес груза.
P man L
W
2 PL
W
P man L
man P L
W
W
5. Тело весом Р равномерно вращается вокруг оси О-О.
Правильной расчетной силовой схемой является схема на
рисунке…
6. На балку падает груз. Условие прочности имеет вид…
äèí
max
Ê Ä
äèí
max
ÊÄ
äèí
max
ñò
max
ÊÄ
äèí
ñò
max
max
Ê Ä
39

40.

Раздел 7.
7. На балку падает груз весом Р. Для определения
статического перемещения,
входящего в формулу
динамического коэффициента,
используется расчетная
схема…
8. На балку падает груз. Если абсолютно жесткую опору
С заменить пружиной, то
динамические напряжения в
балке…
уменьшатся
увеличатся
останутся неизменными
увеличатся в два раза
9. На балку падает груз весом Р.
Динамический коэффициент определяется по
статический угол поворота сечения В, вызванный
силой Р
2h
.
ñò
статический прогиб сечения С, вызванный силой Р
формуле Ê Ä 1 1
Физическим смыслом
величины Δст
является…
статический угол поворота сечения С вызванный
силой Р
статический прогиб сечения С, вызванный
максимальной силой взаимодействия между грузом
и балкой
40

41.

Раздел 7.
10. Резонанс – это…
значительное уменьшение амплитуды колебаний из-за больной
разницы частот вынужденных и собственных колебаний системы
состояние колеблющейся систем, при котором максимальное
напряжение цикла в опасной точке равно пределу прочности
материала
состояние колеблющейся систем, при котором максимальное
напряжение цикла в опасной точке равно пределу текучести
материала
многократное увеличение амплитуды колебаний в результате
совпадения частот вынужденных и собственных колебаний
системы
11. Вынужденные колебания
системы вызваны…
весом электродвигателя
центробежной силой несбалансированной массы электродвигателя
весом рамы и электродвигателя
весом несбалансированной массы электродвигателя
41

42.

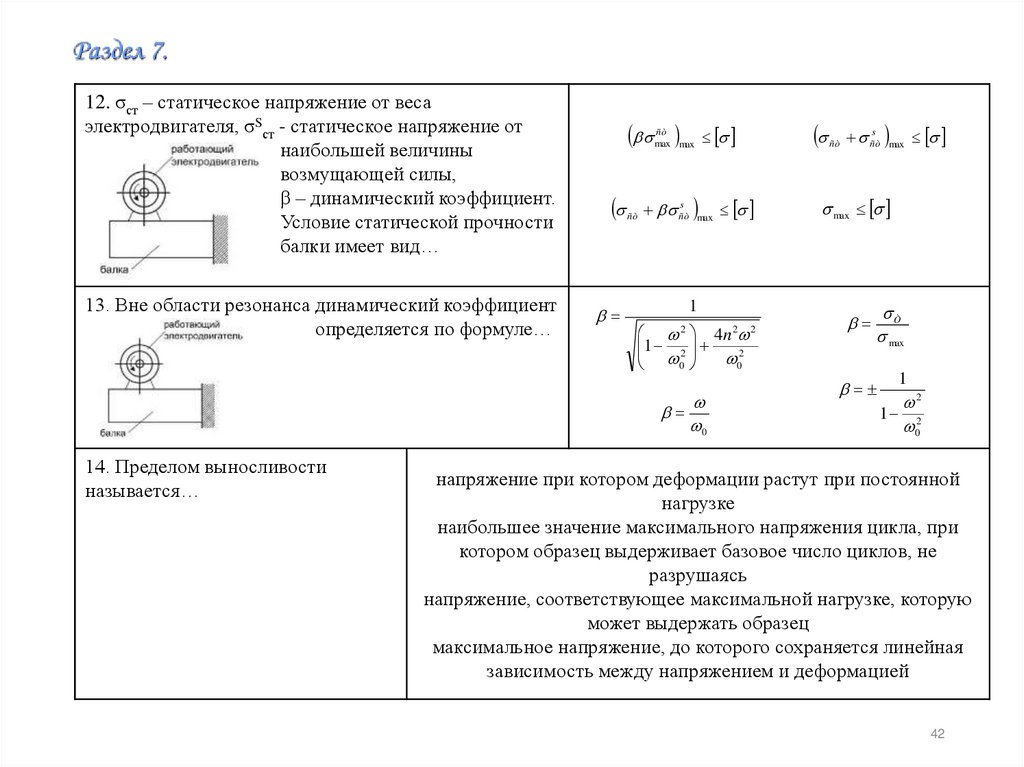
Раздел 7.
12. σст – статическое напряжение от веса
электродвигателя, σSст - статическое напряжение от
наибольшей величины
возмущающей силы,
β – динамический коэффициент.
Условие статической прочности
балки имеет вид…
13. Вне области резонанса динамический коэффициент
определяется по формуле…
ñò
max max
ñò
s
ñò max
1
2 4n 2 2
1 2
02
0
14. Пределом выносливости
называется…
0
ñò
s
ñò max
max
Ò
max
1
1
2
02
напряжение при котором деформации растут при постоянной
нагрузке
наибольшее значение максимального напряжения цикла, при
котором образец выдерживает базовое число циклов, не
разрушаясь
напряжение, соответствующее максимальной нагрузке, которую
может выдержать образец
максимальное напряжение, до которого сохраняется линейная
зависимость между напряжением и деформацией
42

43.

Раздел 7.
15. Среднее напряжение цикла нормальных
напряжений определяется по формуле…
max min
max min
2
4
1
max min
Ê Ä
2
16. σа = 2МПа, σm = 3МПа. График изменения
напряжения во времени имеет вид…
17. Кривая усталости (кривая Вёллера) для
углеродистых сталей имеет вид…
18. Коэффициент запаса усталостной прочности
по нормальным напряжениям определяется по
формуле…
n
n
Ò
max
n
n n
n n
2
2
1
K d a m
n
B
max
43

44.

Раздел 7.
19. Стержень АВ с площадью сечения А из материала с удельным весом
γ равномерно вращается с постоянной угловой
скоростью ω вокруг оси О-О.
Если m = (γ/g)·A – масса единицы длины
стержня, то условие прочности (без учета сил
тяжести стержня) имеет вид…
20.
Укорочение вертикального стержня длиной L,
статически сжатого усилием Р, составляет δ0.
Укорочение этого же стержня в случае
мгновенного приложения нагрузки Р равно…
m 2 L2
2A
m 2 L
2A
m 2 L2
A
2m 2 L2
2A
2 L
0
L
0 1 1
0
0 1 1
2 0
21. Дифференциальное уравнение движения упругой
системы с одной степенью свободы x 2n x P0 sin t
m
является уравнением…
22. Амплитуда σа цикла напряжений связана с
максимальным σmax и минимальным σmin
напряжениями цикла зависимостью…
0
0
2 L
- вынужденных колебаний с учетом сил
сопротивления
- гармонических колебаний без учета сил
сопротивления
- свободных колебаний с учетом сил
сопротивления
- свободных колебаний без учета сил
сопротивления
à
max min
2
à max min
à
à
max min
2
1
max
1
min
СОДЕРЖАНИЕ
44

45.

Раздел 8. Статически неопределимые системы.
1. При расчете методом сил
составляются…
2. При расчете методом сил
устанавливается…
трансцендентные уравнения
дифференциальные уравнения
канонические и дифференциальные уравнения
канонические уравнения
степень статической неопределимости системы
степень статической определимости системы
число опорных связей системы
число шарниров в системе
3. Число канонических уравнений
определяется…
числом опорных реакций
степенью статической неопределимости системы
числом внутренних сил, действующих в сечении элемента
по виду расчетной схемы
4. Если система пять раз статически
неопределима, то составляются…
два канонических уравнения
одно каноническое уравнение
пять канонических уравнений
семь канонических уравнений
45

46.

Раздел 8.
5. Последовательность расчета методом
сил…
1) записываются канонические уравнения
2) составляется основная система
3) определяется степень статической неопределимости
1) составляется основная система
2) определяется степень статической неопределимости
3) записываются канонические уравнения
1) строятся эпюры изгибающих моментов
2) записываются канонические уравнения
3) составляется основная система
1) определяется степень статической неопределимости
2) составляется основная система
3) записываются канонические уравнения
6. Степень статической неопределимости системы,
изображенной на рисунке, равна…
2
1
4
3
7. Для данной статически неопределимой балки
(изображенной на рисунке), основной системой
является схема…
46

47.

Раздел 8.
8. Статически неопределимая система
изображена на рисунке…
9. Степень статической неопределимости системы,
изображенной на рисунке,
равна…
10. Степень статической неопределимости системы,
изображенной на рисунке, равна…
11. Неизвестная X1
каноническом уравнении
δ11X1+Δ1P=0 определяет…
5
3
1
2
3
6
1
4
реакцию отброшенной связи
внешнюю нагрузку
единичное и грузовое перемещение в месте отброшенной связи
перемещение в месте отброшенной связи
47

48.

Раздел 8.
12. Физический смысл свободного члена Δ1P в
каноническом уравнении δ11X1+Δ1P=0
заключается в следующем…
единичное перемещение в направлении
отброшенной связи
сумма перемещений в направлении отброшенной
связи
обобщенная реакция отброшенной связи
обобщенное перемещение в направлении
отброшенной связи от действия внешней нагрузки
13. Коэффициент δ11 в каноническом уравнении
δ11X1+Δ1P=0 определяет…
грузовое перемещение
суммарное перемещение от действия силы X1 и
внешней нагрузки
реакцию от действия силы X1
обобщенное единичное перемещение в
направлении действия силы X1 от силы X1 1
48

49.

Раздел 8.
14. При нагружении стержня получены эпюры изгибающих моментов
от внешних сил МР и от единичной силы Ì , приведенные на
рисунке. Результат вычисления интеграла M P M dz по способу
Верещагина имеет вид…
2
Ml h
3
1
h
Ml h
2
2
Ml h
Ml
15. При нагружении стержня получены эпюры изгибающих моментов
от внешних сил МР и от единичной силы Ì , приведенные на
рисунке. Результат вычисления интеграла M P M dz по способу
Верещагина имеет вид…
h
2
2 2
Pl h
3
1 2
Pl h
3
Pl 2 h
1 2 h
Pl
3
2
49

50.

Раздел 8.
16. При нагружении стержня получены эпюры изгибающих моментов от
внешних сил МР и от единичной силы Ì , приведенные на рисунке.
Результат вычисления интеграла M P M dz по способу Верещагина
имеет вид…
17. При нагружении стержня получены эпюры изгибающих моментов от
внешних сил МР и от единичной силы Ì , приведенные на рисунке.
Результат вычисления интеграла M P M dz по способу Верещагина
имеет вид…
h
2
1
Ml h
3
Ml h
2
Ml h
3
Pl 2 h
2 2
Pl h
3
1 2
Pl h
3
1 2 h
Pl
3
2
Pl 3
4 EJ
2 Pl 3
EJ
Pl 2
EJ
Pl 3
16 EJ
Ml
18. Свободный член Δ1P канонического уравнения δ11X1+Δ1P=0 равен…
50

51.

Раздел 8.
19.
Прогиб среднего сечения шарнирно
опертой балки (p, l, EJx – известны)
равен…
Pl 3
48EJ õ
20. Статически неопределимой является система…(… раз неопределима).
21.
Pl 3
4 EJ õ
Pl 3
8 EJ õ
Pl 3
EJ õ
3, (1)
1, (2)
2, (2)
4, (1)
Для схемы, изображенной на
рисунке, правильно
составлена эквивалентная
система…
22. Эпюра изгибающих моментов для статически
неопределимой балки, показанной на рисунке, имеет
вид…
СОДЕРЖАНИЕ
51

52.

Раздел 9. Устойчивость сжатых стержней.
1. Упругое равновесие сжатого стержня
устойчиво, если стержень…
при любом малом отклонении от состояния
равновесия стремится возвратиться к
первоначальному состоянию после снятия
воздействия, вызывающего это отклонение
изгибается в произвольной плоскости
находится в безразличном равновесии: может
сохранять прямолинейную форму упругого
равновесия, но может и потерять её от малейшего
воздействия
продолжает деформироваться в направлении
вызванного малого отклонения
2. Вывод формулы Эйлера основан на
допущении…
3. Условие применимости формулы Эйлера
имеет вид…
напряжения превышают предел текучести
деформации подчиняются закону Гука
в стержне возникают пластические деформации
напряжения достигают предел текучести
êð
Ðêð
êð
Ðêð
À
À
Ò
êð
Ðêð
Ò
êð
Ðêð
À
À
ïö
ïö
52

53.

Раздел 9.
4. Для стержней из малоуглеродистой стали
формула Эйлера для критической силы
применима, если гибкость стержня…
5. Коэффициент приведенной длины стержня при
вычислении критической силы по формуле
Эйлера зависит от…
6. Величина λ=μl / imin, которая входит в формулу
для критического напряжения в сжатом стержне
σкр=π2E / λ2, называется…
7. График зависимости критического напряжения
σкр от гибкости сжатого стержня в пределах
применимости формулы Эйлера представляет
собой…
меньше 100
равна 50
больше 100
меньше 50
величины приложенной силы
формы поперечного сечения стержня
способа закрепления стержня
материала стержня
характеристикой продольного изгиба
гибкостью стержня
жесткостью
податливостью
дугу окружности
параболу
гиперболу
прямую линию
53

54.

Раздел 9.
8. Приведенная на рисунке форма потери
устойчивости сжатого стержня соответствует
способу закрепления стержня, показанному на
схеме…
9. При сжатии упругого стержня, показанного на
рисунке, силой Р-Ркр форма потери устойчивости
стержня имеет вид…
10. При сжатии упругого стержня, показанного на
рисунке, силой Р-Ркр форма потери устойчивости
стержня имеет вид…
11. Для показанного на рисунке способа закрепления
стержня коэффициент приведенной длины μ при
вычислении критической силы по формуле Эйлера равен…
μ=1
μ=2
μ = 0,5
μ = 0,7
54

55.

Раздел 9.
12. Формой потери устойчивости стержня при
шарнирном опирании его концов является…
синусоида
гипербола
парабола
дуга окружности
13. Для сжатого стержня с шарнирно
закрепленными концами коэффициент
приведенной длины μ при расчете на
устойчивость равен…
0,7
0,5
2
1
14. Основным критерием определения
критического напряжения за пределом
пропорциональности является…
длина
статический момент
площадь сечения
гибкость
15. При расчете на устойчивость сжатых
стержней за пределом пропорциональности
используется формула…
16. Формулу Ясинского используют при
расчетах на…
определения момента инерции
Эйлера
Ясинского
определения гибкости
жесткость
прочность при растяжении
прочность при сдвиге
устойчивость сжатых стержней за пределом
пропорциональности
55

56.

Раздел 9.
17. Коэффициент приведенной длины стержня при
вычислении критической силы по формуле Эйлера
зависит от…
18. Вывод формулы Эйлера для критической силы
сжатого стержня основан на предположении, что под
действием сжимающей силы, равной критической
силе, стержень изогнется, при этом…
материала стержня
формы поперечного сечения
величины приложенной силы
способа закрепления стержня
- в стержне возникают пластические деформации
- напряжения достигают предел текучести
- напряжения превышают предел текучести
- деформации подчиняются закону Гука
19. При сжатии упругого стержня, показанного
на рисунке, силой Р ≥ Ркр форма потери
устойчивости стержня имеет вид…
20. Стержень длиной l = 2,0м с промежуточным шарнирным закреплением сжат
силой Р. Зависимость критического напряжения от гибкости λ для стали Ст. 3
приведена на рисунке.
200МПа
227 МПа
232 МПа
240 МПа
Поперечное сечение стержня представляет собой швеллер №10, радиусы инерции
которого ix = 3,99см, iy = 1,37см. Критическое напряжение для стержня равно…
СОДЕРЖАНИЕ
56

57.

Список рекомендуемой литературы
1. Феодосьев В.И. Сопротивление материалов. М.: Наука, 1974 г.
2. Беляев М.Н. Сопротивление материалов. М.: Наука, 1976 г.
3. Писаренко Г.С. Сопротивление материалов. Киев: Вища школа,
1976 г.
4. Вольмир А.С. Сборник задач по сопротивлению материалов. М.:
Наука, 1984 г.
5. Лихарев К.К., Сухова Н.А. Сборник задач по курсу «Сопротивление
материалов»: учебное пособие для машиностроительных вузов.–
М.:Машиностроение, 1980г.–224 стр.
6. Справочник по сопротивлению материалов/ Писаренко Г.С.,
Яковлев А.П., Матвеев В.В. – Киев: Наукова думка, 1988г. – 736 с.
СОДЕРЖАНИЕ
57