Похожие презентации:
Сопротивление материалов. Основные понятия
1.
МЕ
Х
А
Н
И
К
А
Модуль 2.
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Раздел 6. Основные понятия
Раздел 7. Простейшие виды деформаций
Раздел 8. Сложное сопротивление
Раздел 9. Прочность при переменных и
динамических напряжениях
Раздел 10. Устойчивость
Лекционный курс - 34 час
Лабораторные занятия – 17 час
Самостоятельная работа : - Выполнение и защита РГЗ
2. Раздел 6. - Основные понятия сопротивления материалов
МЕХАНИКАСопротивление материалов
Модуль 2
Раздел 6. - Основные понятия
сопротивления материалов
Общие сведения
ЛЕКЦИЯ 1
ЛЕКЦИЯ 2
3. ЛЕКЦИЯ 1 План:
МЕХАНИКА1.1
Модуль 2
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ОСНОВНЫЕ ПОНЯТИЯ
СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Основные понятия и определения
ЛЕКЦИЯ 1
План:
1.1 Основные определения
1.2 Допущения (гипотезы) в сопротивлении материалов
1.3 Внешние силы
1.4 Внутренние силы. Метод сечений.
4. Сопротивление материалов - наука о методах расчетов на прочность, жесткость и устойчивость элементов машин и сооружений
1.2ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Сопротивление материалов - наука
о методах расчетов на прочность, жесткость и
устойчивость элементов машин и сооружений
Прочность – это способность элемента
конструкции сопротивляться разрушению под
нагрузкой.
Жесткость – это способность элемента
конструкции сопротивляться деформациям.
Устойчивость – это способность элемента
конструкции сопротивляться воздействию
больших отклонений от равновесия при малых
изменениях нагрузки.
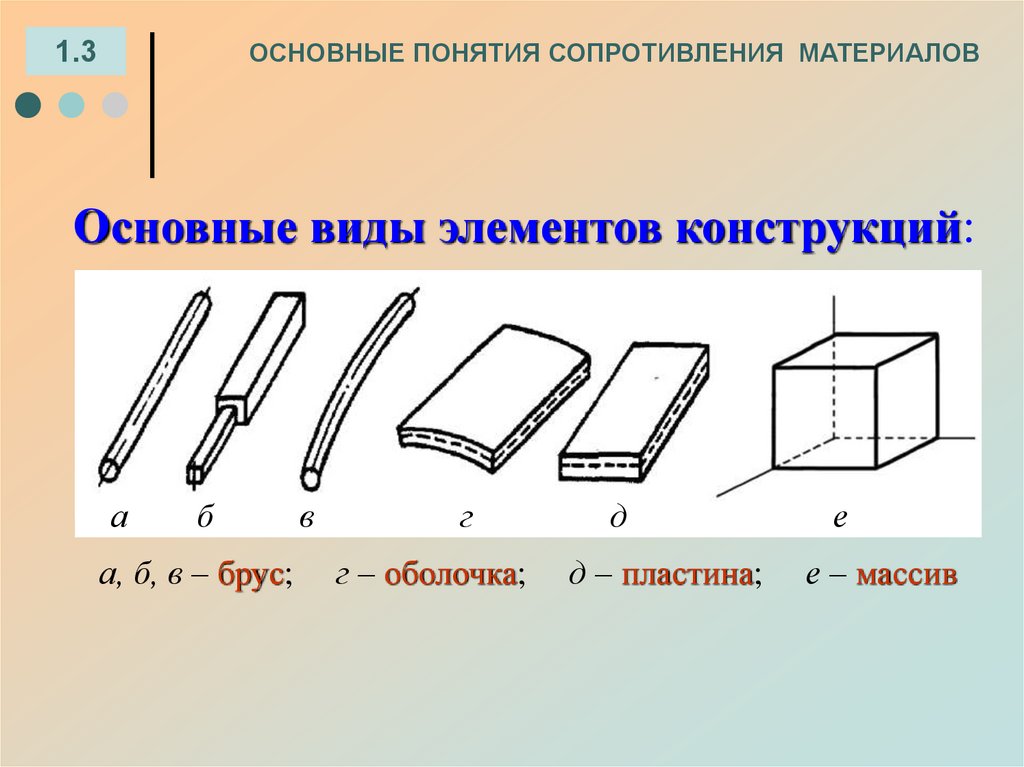
5. Основные виды элементов конструкций:
ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ1.3
Основные виды элементов конструкций:
а
б
а, б, в – брус;
в
г
г – оболочка;
д
д – пластина;
е
е – массив
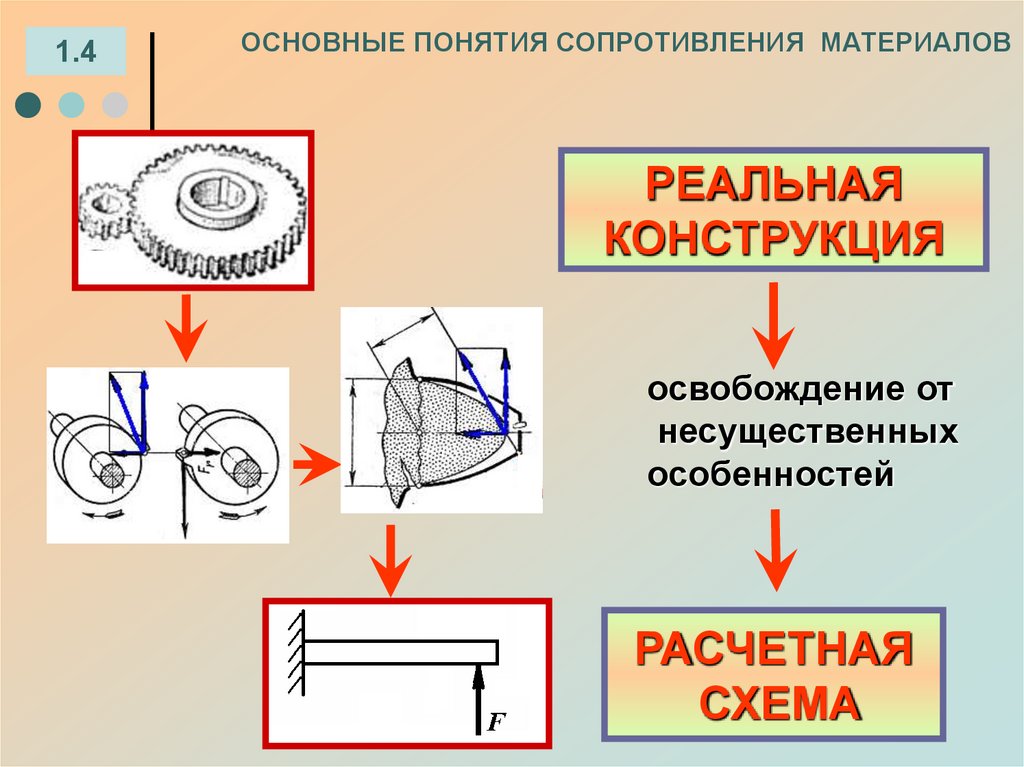
6. РЕАЛЬНАЯ КОНСТРУКЦИЯ
1.4ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
РЕАЛЬНАЯ
КОНСТРУКЦИЯ
освобождение от
несущественных
особенностей
РАСЧЕТНАЯ
СХЕМА
7. Гипотезы (допущения) сопротивления материалов
1.5ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Гипотезы (допущения)
сопротивления материалов
сплошности
однородности
изотропности
независимости действия сил
малости деформаций
внутренних усилий
8. ВНЕШНИЕ СИЛЫ (нагрузки)
1.6ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
ВНЕШНИЕ СИЛЫ
(нагрузки)
активные и реактивные
сосредоточенные и
распределенные (линейно, поверхностно,
объемно распределенные)
статические и динамические
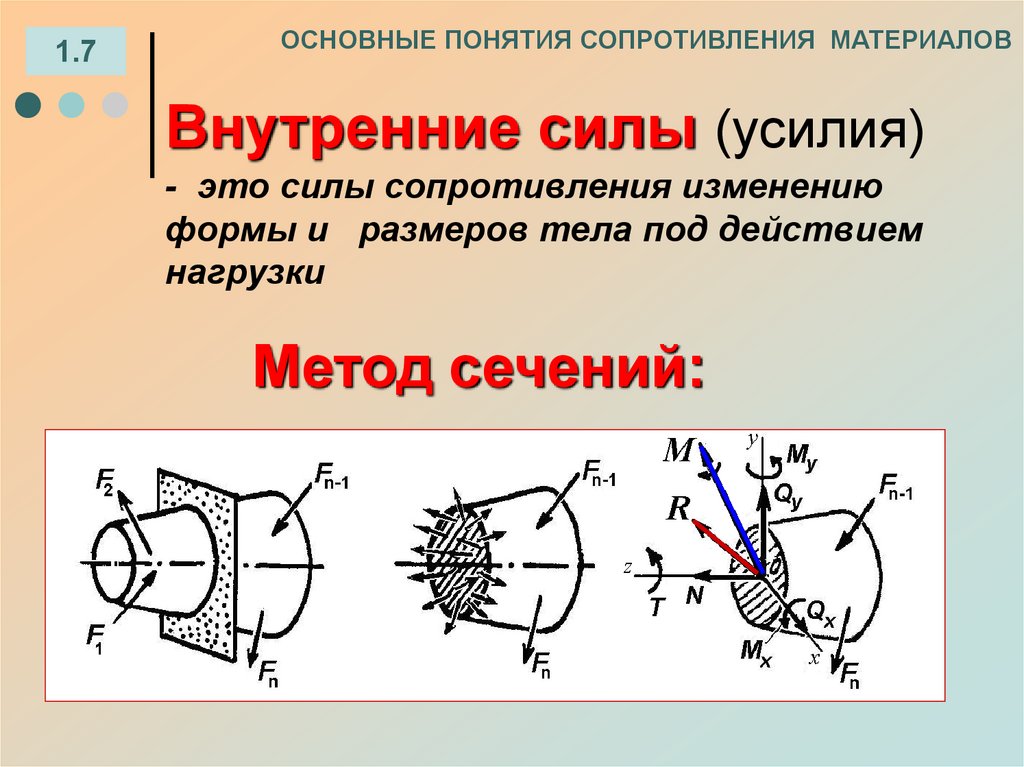
9. Внутренние силы (усилия)
1.7ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Внутренние силы (усилия)
- это силы сопротивления изменению
формы и размеров тела под действием
нагрузки
Метод сечений:
10. (ВСФ)
ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ1.8
Внутренние силовые факторы (ВСФ)
________________________________________________________
ВСФ
Вид деформации
продольная сила N
«растяжение» или «сжатие»
поперечная сила Q
«чистый сдвиг».
крутящий момент Т
«кручение»
изгибающий момент М
- «чистый изгиб»
комбинированные
виды нагружения
«сложное сопротивление».
________________________________________________________
Эпюры ВСФ - графики изменения внутренних силовых
факторов вдоль оси бруса
11. План построения эпюры ВСФ
1.9ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Внутренние силы.
Метод сечений
План построения эпюры ВСФ
1.
Вычерчивают схему нагружения стержня.
2.
Определяют реакции связей
3.
Выявляют «характерные участки» стержня
4.
Применяя метод сечений на каждом характерном
участке, составляют уравнения ВСФ по длине участка
5.
Строят графики зависимостей ВСФ
12. ЛЕКЦИЯ 2 План
МЕХАНИКА2.1
Модуль 2
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ОСНОВНЫЕ ПОНЯТИЯ
СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Основные понятия и определения
ЛЕКЦИЯ 2
План
2.1. Напряжения.
2.2. Перемещения и деформации.
2.3. Закон Гука.
2.4. Условия прочности и жесткости в общем виде
13. ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
2.2ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
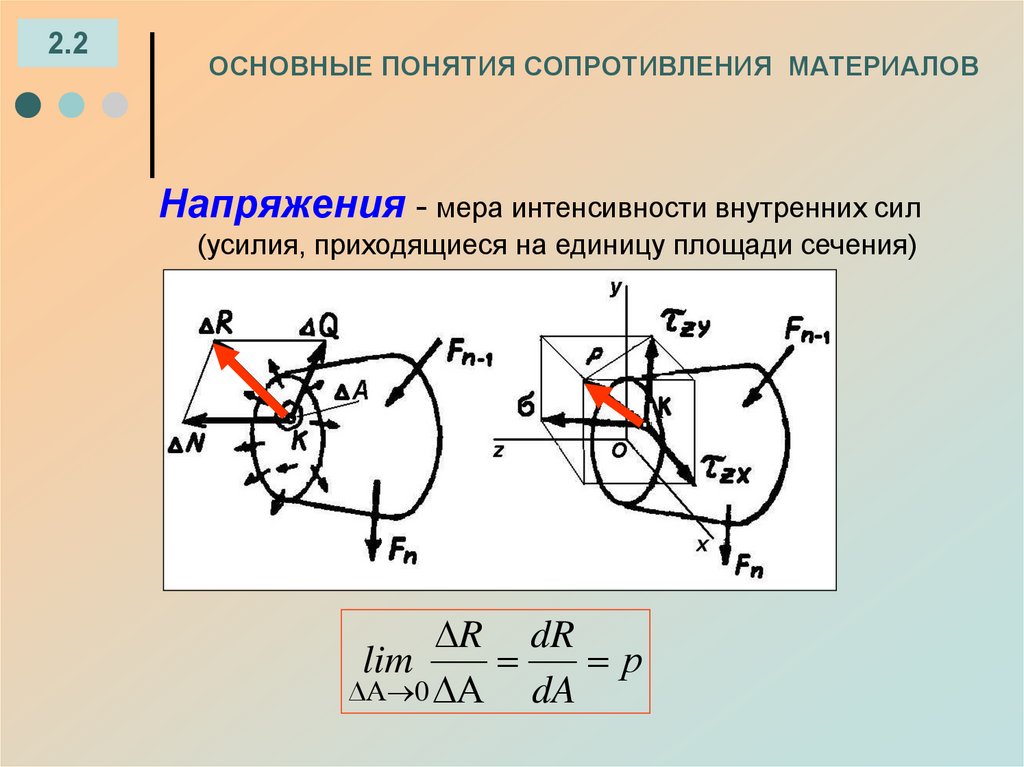
Напряжения - мера интенсивности внутренних сил
(усилия, приходящиеся на единицу площади сечения)
R dR
lim
р
0
dA
14. ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
2.3ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
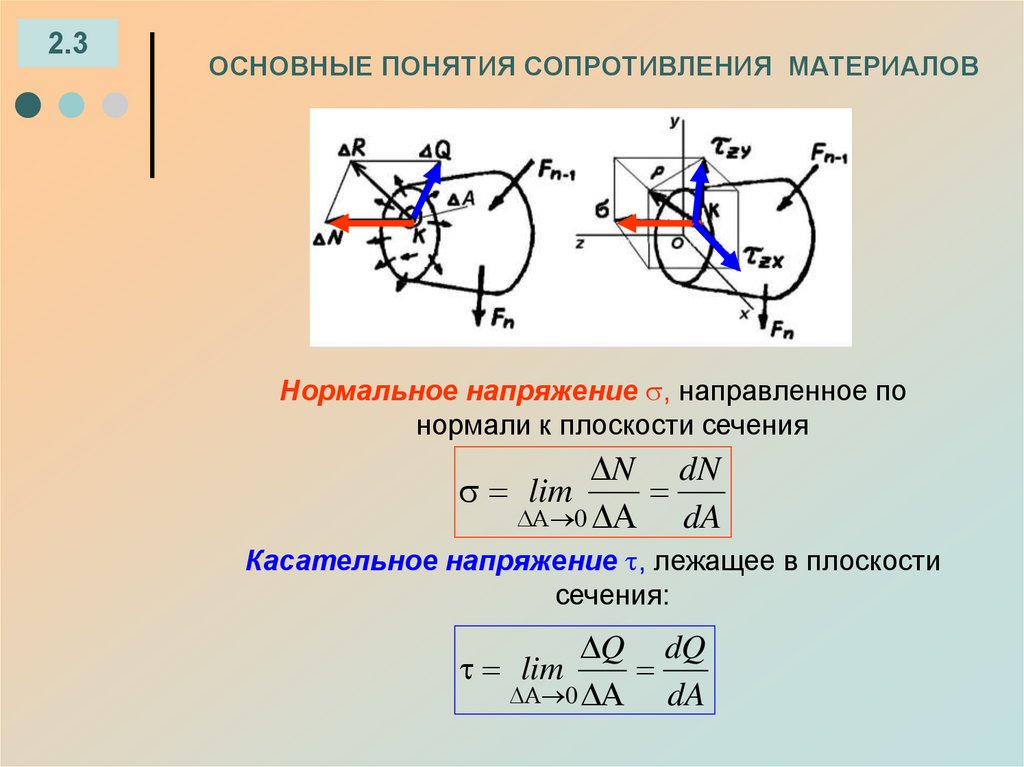
Нормальное напряжение , направленное по
нормали к плоскости сечения
N dN
lim
0
dA
Касательное напряжение , лежащее в плоскости
сечения:
Q dQ
lim
0
dA
15. ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
2.4ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
Связь напряжений и ВСФ
dA
A
Qx zx dA
Qy zy dA
zx y zy x dA
A
x y dA
A
y x dA
A
где x и y – координаты точки в поперечном сечении
__________________________________________
Паскаль (1 Па = 1 Н/м2).
Мегапаскаль (1 МПа = 106 Па = 106 Н/м2 =1 Н/мм2.
16. ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
2.5ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
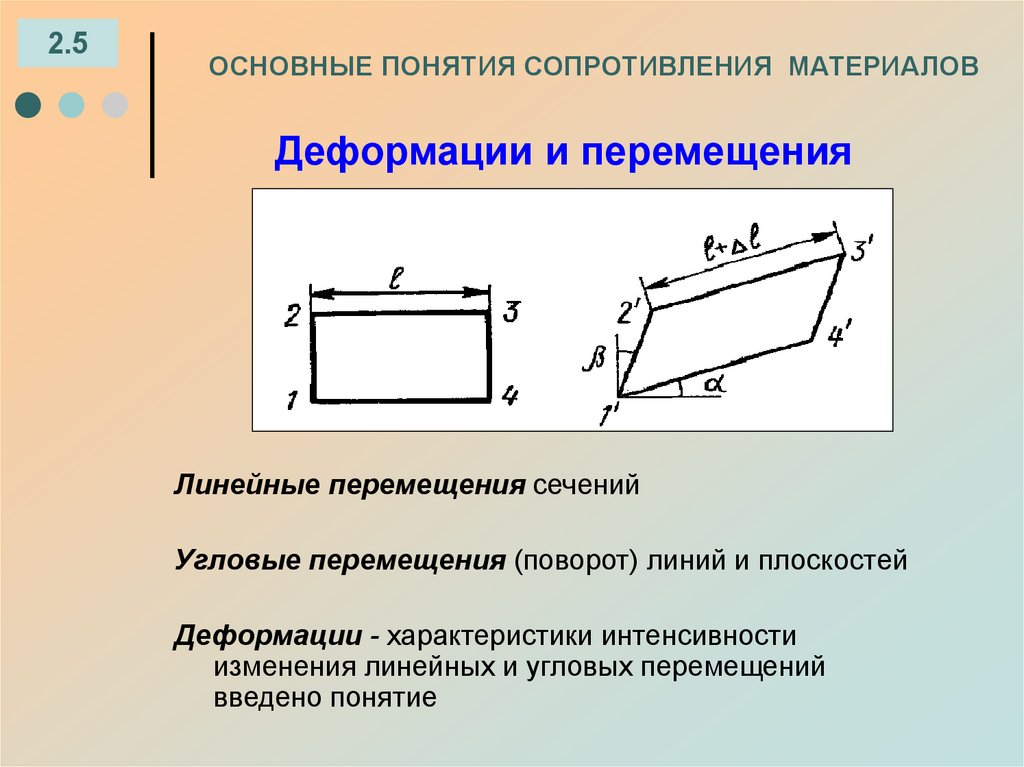
Деформации и перемещения
Линейные перемещения сечений
Угловые перемещения (поворот) линий и плоскостей
Деформации - характеристики интенсивности
изменения линейных и угловых перемещений
введено понятие
17. ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
2.6ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
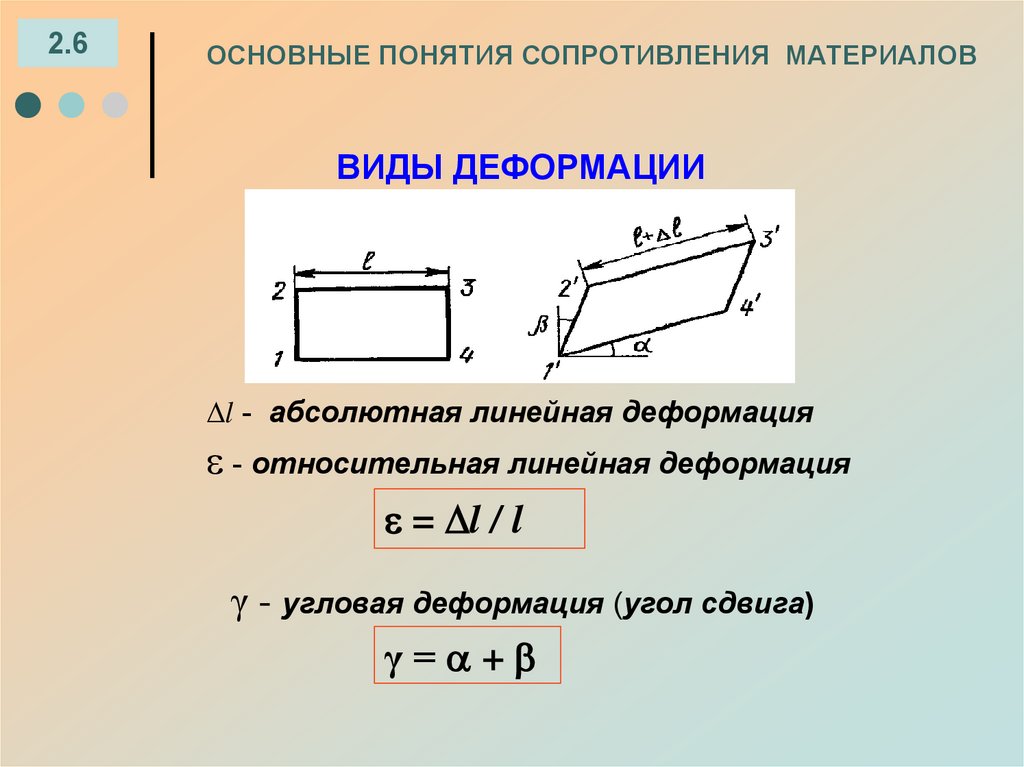
ВИДЫ ДЕФОРМАЦИИ
l - абсолютная линейная деформация
- относительная линейная деформация
= l / l
γ - угловая деформация (угол сдвига)
γ= +
18. ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
2.7ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
ХАРАКТЕР ДЕФОРМАЦИИ
Остаточные (пластические) деформации не
исчезают после снятия нагрузки
Упругие деформации исчезают после разгрузки
Закон Гука:
E Е - модуль Юнга (модуль продольной
упругости)
G
G - модуль сдвига
19. ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
2.8ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
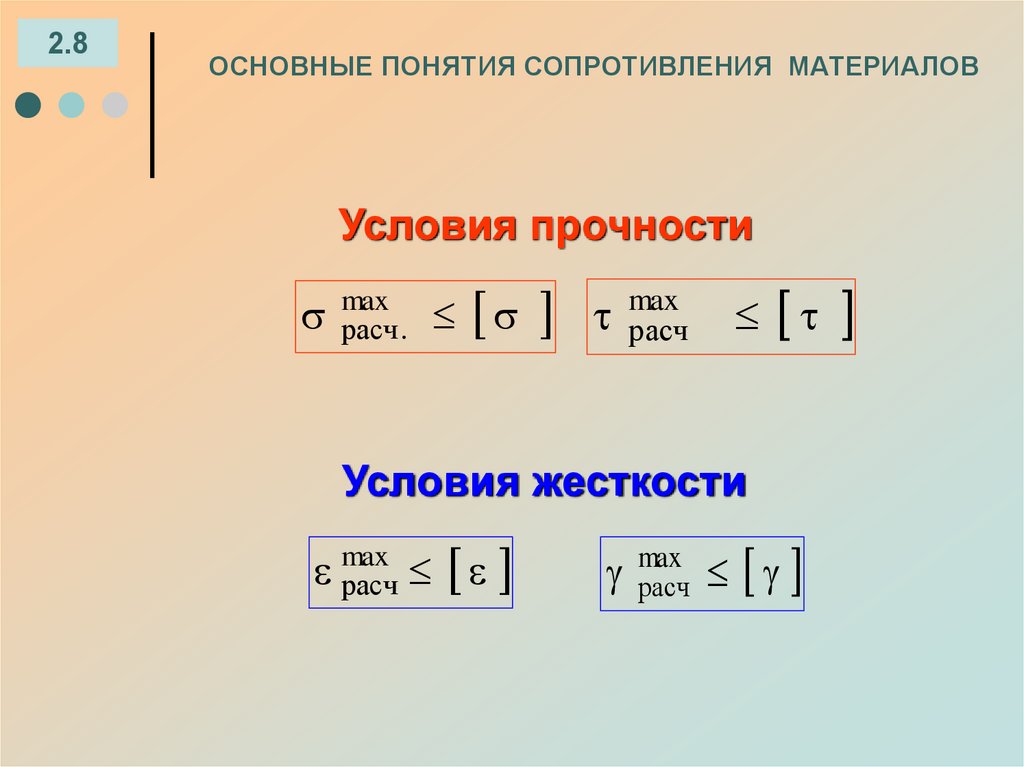
Условия прочности
max
max
расч .
расч
Условия жесткости
max
расч
max
расч
20. Раздел 7 - Простейшие виды деформации
МЕХАНИКАСопротивление материалов
Модуль 2
Раздел 7 - Простейшие виды деформации
Растяжение и сжатие
ЛЕКЦИЯ 3
Механические испытания
конструкционных материалов
ЛЕКЦИЯ 4
Геометрические характеристики
плоских сечений
ЛЕКЦИЯ 5
Чистый сдвиг. Кручение
ЛЕКЦИЯ 6
Изгиб
ЛЕКЦИЯ 7
ЛЕКЦИЯ 8
ЛЕКЦИЯ 9
21. ЛЕКЦИЯ 3 План:
МЕХАНИКА3.1
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ПРОСТЕЙШИЕ ВИДЫ ДЕФОРМАЦИИ
Растяжение и сжатие
ЛЕКЦИЯ 3
План:
3.1. Внутренние усилия при растяжении-сжатии
3.2. Напряжения при растяжении-сжатии
3.3. Деформации при растяжении-сжатии
3.4. Условия прочности и жесткости при растяжении и сжатии
22. РАСТЯЖЕНИЕ И СЖАТИЕ
3.2РАСТЯЖЕНИЕ И СЖАТИЕ
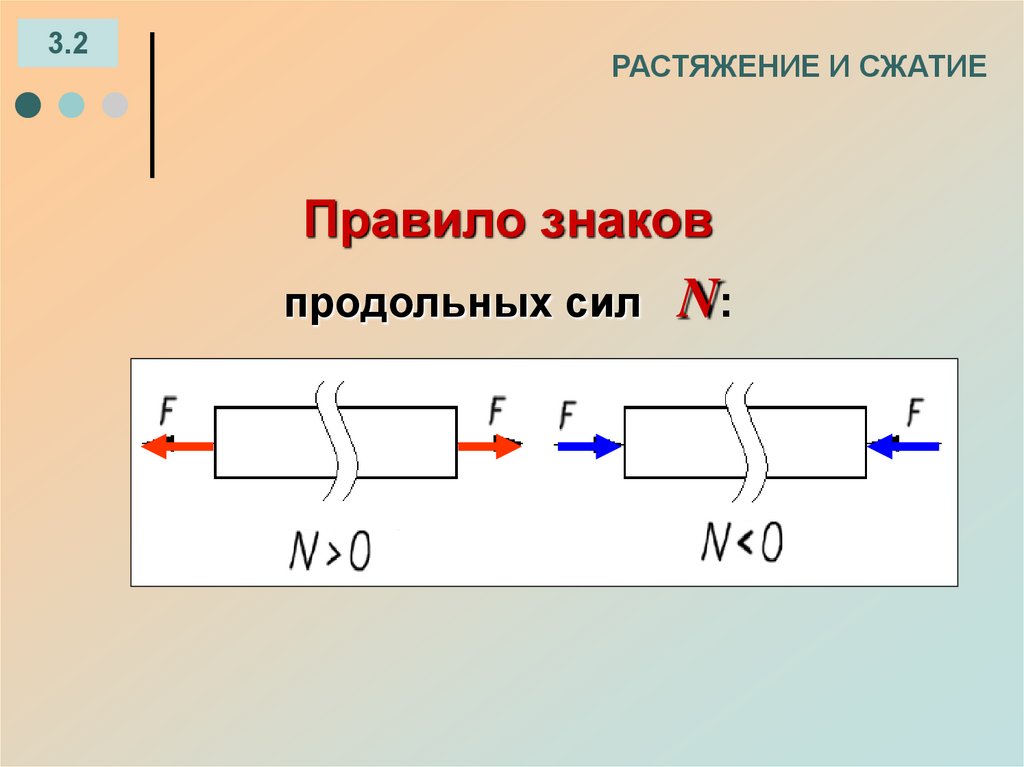
Правило знаков
продольных сил
N:
23. РАСТЯЖЕНИЕ И СЖАТИЕ
3.3РАСТЯЖЕНИЕ И СЖАТИЕ
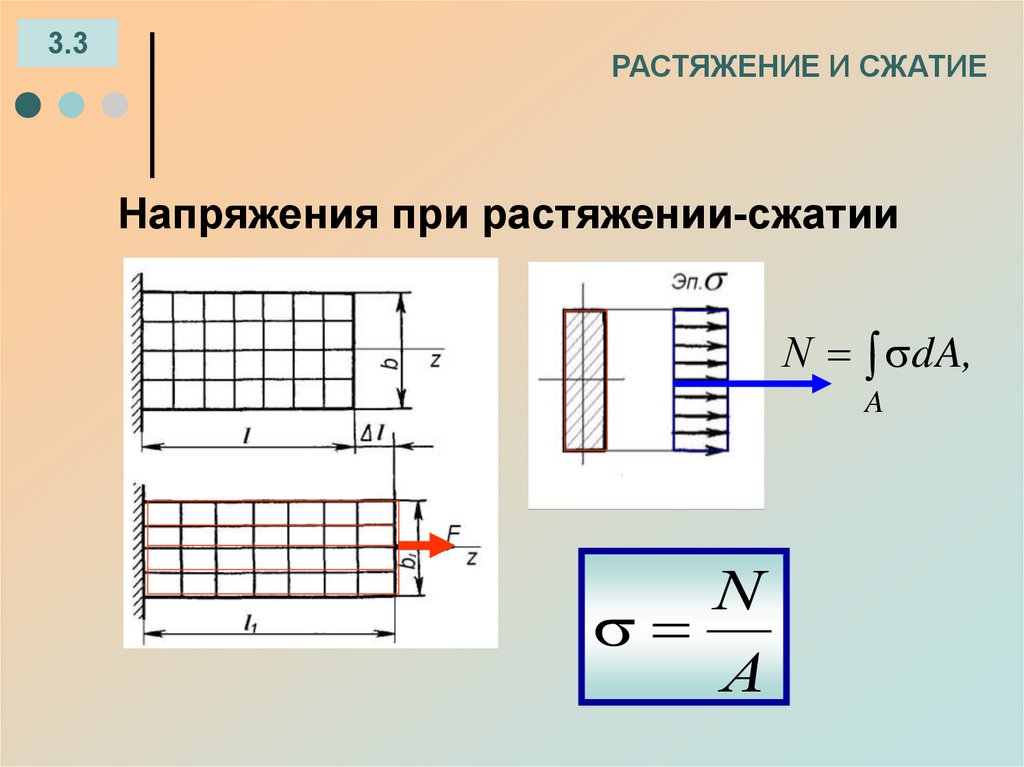
Напряжения при растяжении-сжатии
Ν dA,
A
Ν
Α
24. РАСТЯЖЕНИЕ И СЖАТИЕ
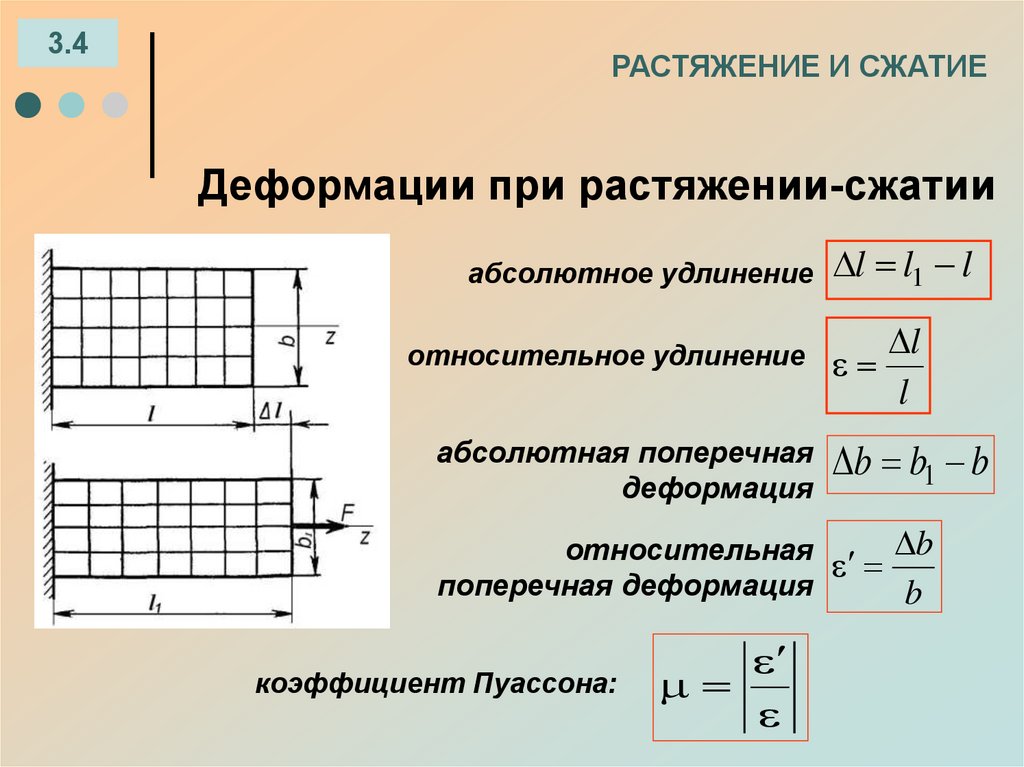
3.4РАСТЯЖЕНИЕ И СЖАТИЕ
Деформации при растяжении-сжатии
абсолютное удлинение l l1 l
относительное удлинение
l
l
абсолютная поперечная b b b
1
деформация
относительная b
поперечная деформация
b
коэффициент Пуассона:
25. РАСТЯЖЕНИЕ И СЖАТИЕ
3.5РАСТЯЖЕНИЕ И СЖАТИЕ
Коэффициент Пуассона μ
для различных материалов
Модуль продольной упругости Е
для различных материалов
Материал
μ
Сталь
0,25 - 0,33
Медь
0,31 - 0,34
Материал
Е, МПа
Сталь
2 · 105
Медь
Бронза
0,32 – 0,35
1 - 105
Алюминий
0,32 - 0,36
Дерево
1 - 104
Чугун
0,23 - 0,27
Алюминий
0,67 - 105
Камень
0,16 - 0,34
Чугун
1,6 - 105
Бетон
0,08 - 0,18
Мрамор
0,56 -· 105
Фанера
0,07
Пробка
≈0
26. РАСТЯЖЕНИЕ И СЖАТИЕ
3.6РАСТЯЖЕНИЕ И СЖАТИЕ
Деформации при растяжении-сжатии
закон Гука:
= Е · ,
где:
Ν
,
Α
l
l
абсолютное удлинение
стержня
Νl
l
ΕΑ
N dl
l
0 E A
l
(Е·А) - жесткость сечения
стержня
27. РАСТЯЖЕНИЕ И СЖАТИЕ
3.7РАСТЯЖЕНИЕ И СЖАТИЕ
Условие прочности стержня
max = Nmax/A ≤ [ ].
Условие жесткости стержня
l ≤ [ l],
28. ЛЕКЦИЯ 4 План:
4.1МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ПРОСТЕЙШИЕ ВИДЫ ДЕФОРМАЦИИ
Механические испытания конструкционных
материалов
ЛЕКЦИЯ 4
План:
4.1. Диаграммы растяжения
4.2. Пластическое и хрупкое разрушение материала
4.3. Испытание на сжатие
4.4. Испытание на твердость
4.5. Ползучесть, релаксация и длительная прочность материала
4.6. Допускаемые напряжения. Коэффициент запаса прочности
29. МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ
4.2МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ КОНСТРУКЦИОННЫХ
МАТЕРИАЛОВ
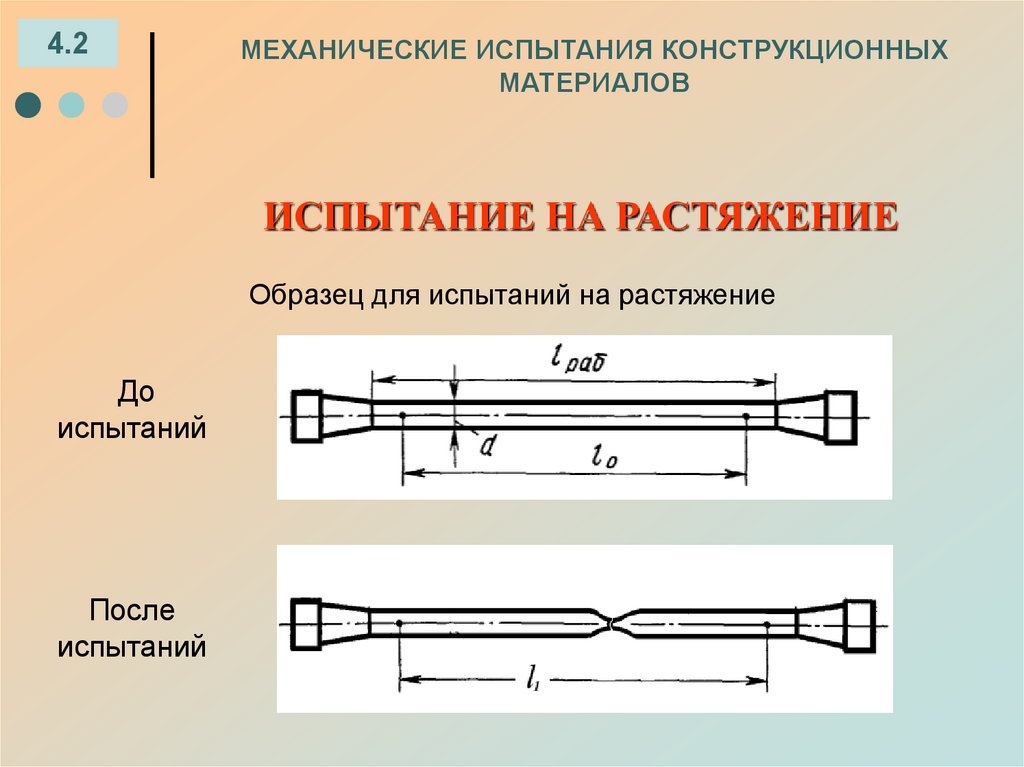
ИСПЫТАНИЕ НА РАСТЯЖЕНИЕ
Образец для испытаний на растяжение
До
испытаний
После
испытаний
30. МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ
4.3МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ КОНСТРУКЦИОННЫХ
МАТЕРИАЛОВ
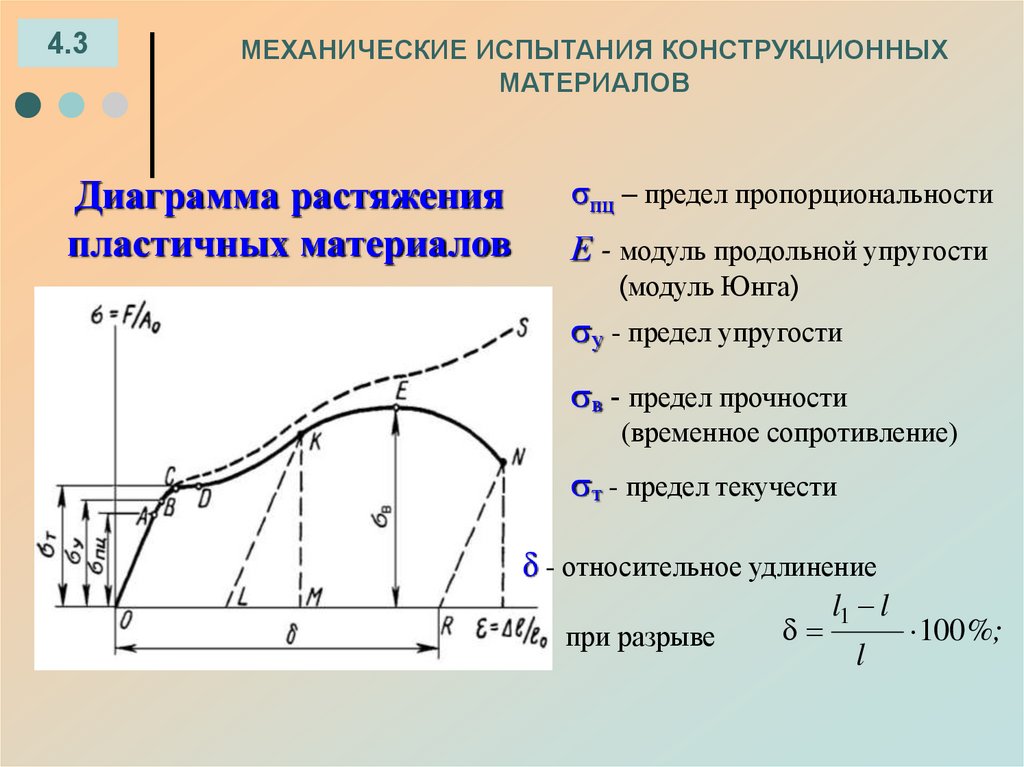
Диаграмма растяжения
пластичных материалов
σпц – предел пропорциональности
Е - модуль продольной упругости
(модуль Юнга)
у - предел упругости
в - предел прочности
(временное сопротивление)
т - предел текучести
δ - относительное удлинение
при разрыве
l1 l
l
100 %;
31. МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ
4.4МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ КОНСТРУКЦИОННЫХ
МАТЕРИАЛОВ
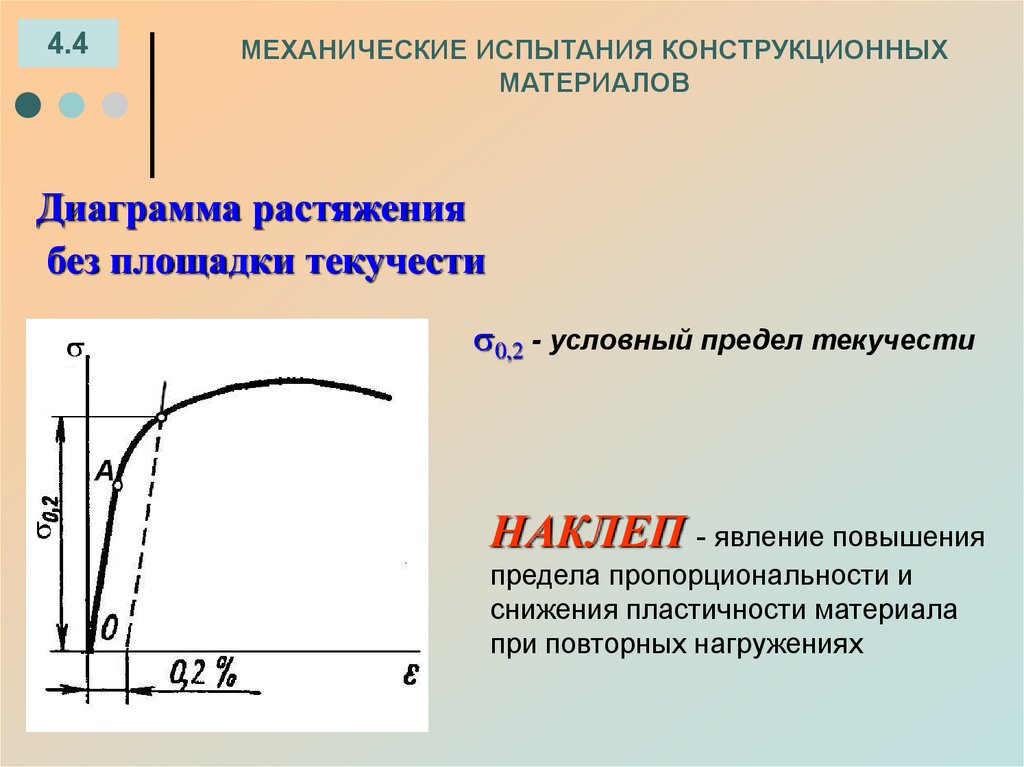
Диаграмма растяжения
без площадки текучести
0,2 - условный предел текучести
НАКЛЕП - явление повышения
предела пропорциональности и
снижения пластичности материала
при повторных нагружениях
32. МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ
4.5МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ КОНСТРУКЦИОННЫХ
МАТЕРИАЛОВ
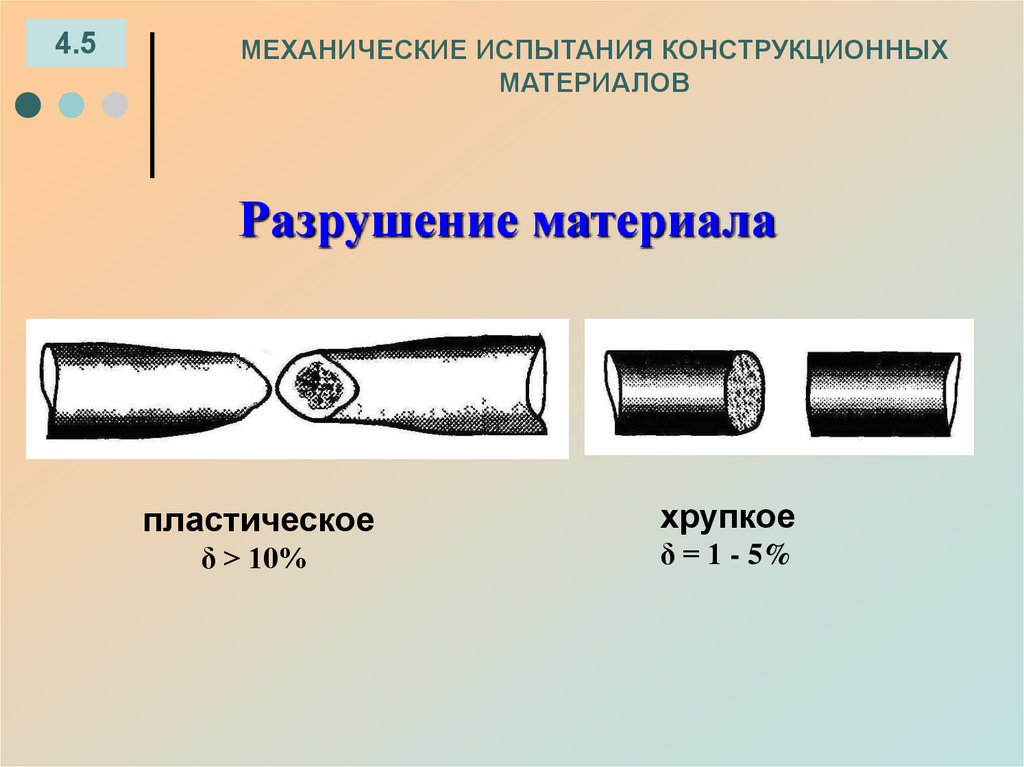
Разрушение материала
пластическое
δ > 10%
хрупкое
δ = 1 - 5%
33. МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ
4.6МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ КОНСТРУКЦИОННЫХ
МАТЕРИАЛОВ
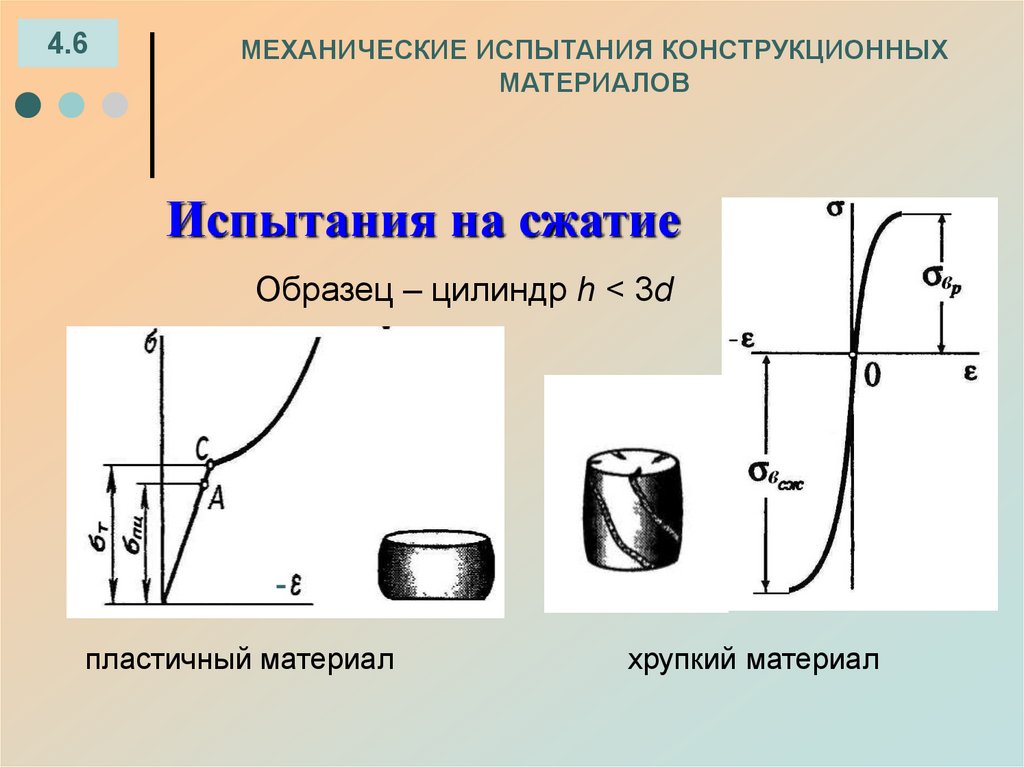
Испытания на сжатие
Образец – цилиндр h < 3d
пластичный материал
хрупкий материал
34. МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ
4.7МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ КОНСТРУКЦИОННЫХ
МАТЕРИАЛОВ
Испытание на твердость
Твердость - способность материала оказывать сопротивление
механическому внедрению в него другого более твердого тела
(индентора).
Метод
Обозначение
Индентор
Измерение
Твердость
по Бринеллю
НВ
Стальной
закаленный
шарик
Диаметр
отпечатка
Твердость
по Роквеллу
HRА, HRВ,
HRC
Алмазный
конус
Глубина
внедрения
HV
Алмазная
пирамида
Диагональ
отпечатка
Твердость
по Виккерсу
35. МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ
4.8МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ КОНСТРУКЦИОННЫХ
МАТЕРИАЛОВ
ПОЛЗУЧЕСТЬ МАТЕРИАЛА - изменение деформаций и
напряжений, возникающих в нагруженной конструкции с
течением времени в условиях не изменяющейся нагрузки
Последействие - рост пластических деформаций
материала при постоянном напряжении.
Релаксация напряжений - процесс уменьшения
напряжений при постоянной величине деформации
материала.
Предел длительной прочности -
900
1000
36. МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ
4.9МЕХАНИЧЕСКИЕ ИСПЫТАНИЯ КОНСТРУКЦИОННЫХ
МАТЕРИАЛОВ
Допускаемые напряжения.
[ ]= np / n
пр - предельные
Для хрупких материалов: ( пр = в),
напряжения
Для пластичных материалов: ( пр = т)
n – коэффициент
для пластичных материалов n = 2...4,
запаса прочности
для хрупких материалов n = 4...6.
37. ЛЕКЦИЯ 5 План:
5.1МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ПРОСТЕЙШИЕ ВИДЫ ДЕФОРМАЦИИ
Геометрические характеристики плоских
сечений
ЛЕКЦИЯ 5
План:
5.1. Статический момент сечения
5.2. Моменты инерции
5.3. Моменты инерции при параллельном переносе и повороте осей
5.4. Главные оси и главные моменты инерции
38. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
5.2ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
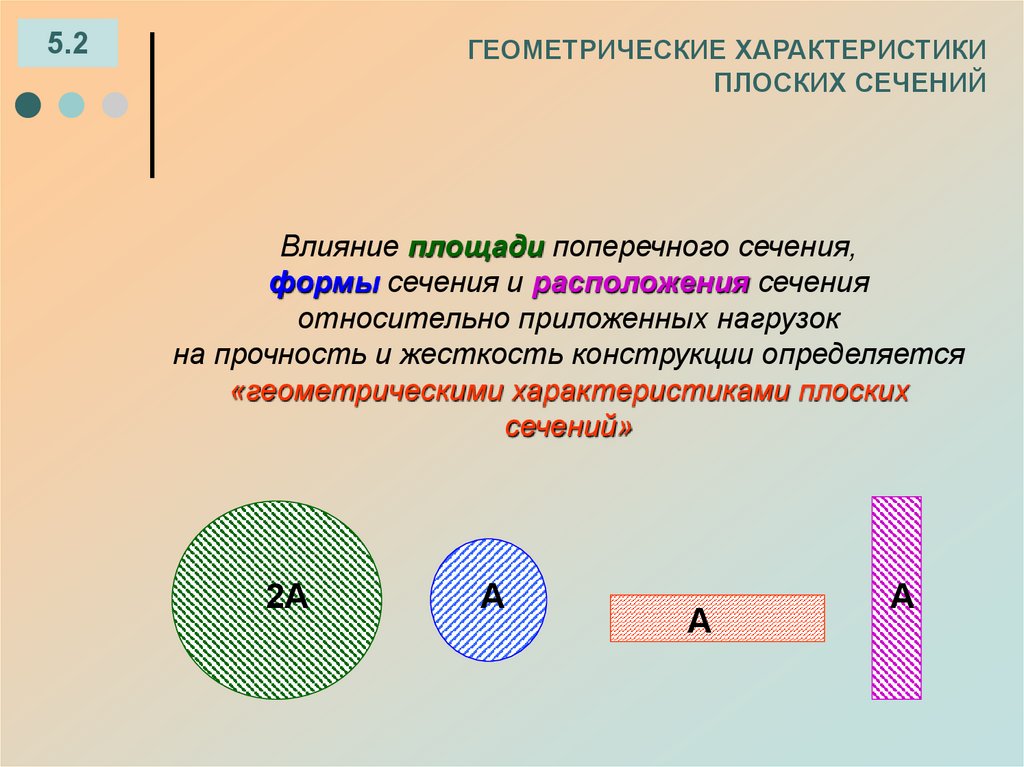
Влияние площади поперечного сечения,
формы сечения и расположения сечения
относительно приложенных нагрузок
на прочность и жесткость конструкции определяется
«геометрическими характеристиками плоских
сечений»
2А
А
А
А
39. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
5.3ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
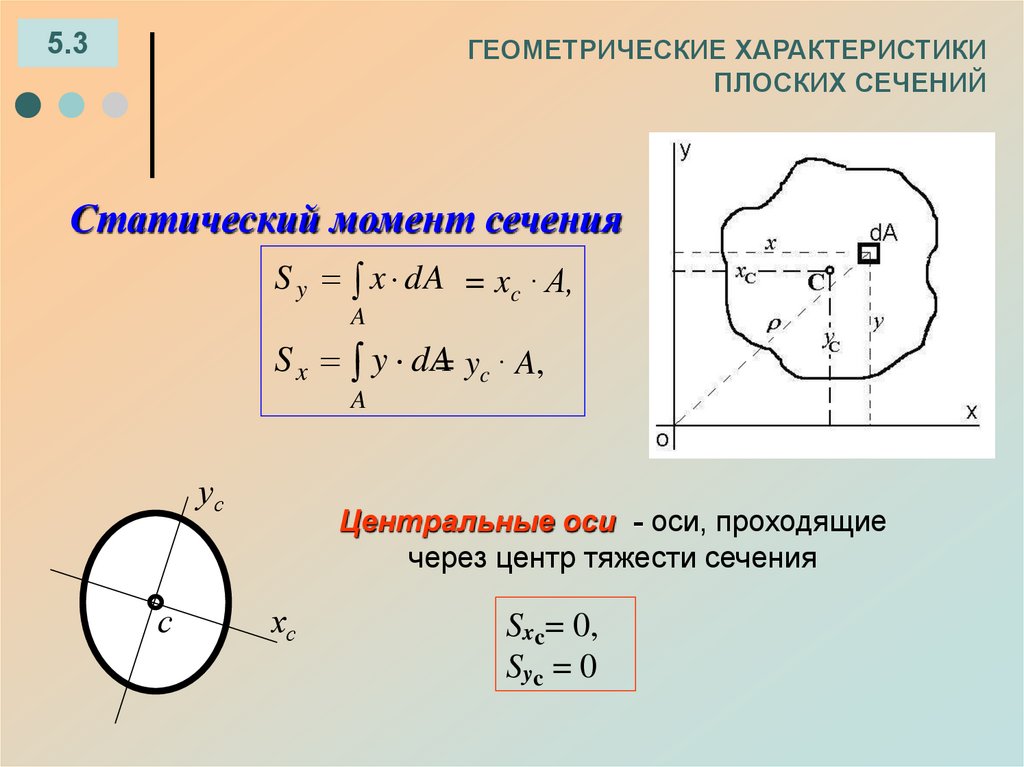
Статический момент сечения
S y x dA = xc · A,
A
S x y dA
= yc · A,
A
ус
с
Центральные оси - оси, проходящие
через центр тяжести сечения
хс
Sxc= 0,
Syc = 0
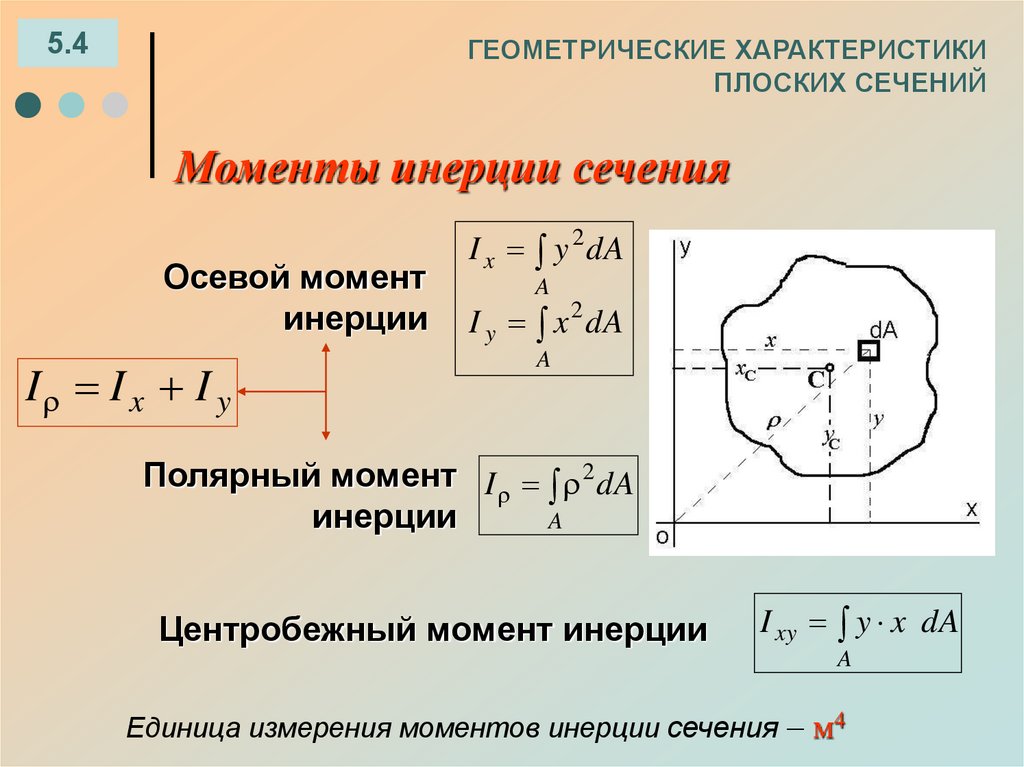
40. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
5.4ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
Моменты инерции сечения
Осевой момент
инерции
I I x I y
I x y 2 dA
A
I y x 2 dA
A
Полярный момент I 2 dA
инерции
A
Центробежный момент инерции
I xy y x dA
A
Единица измерения моментов инерции сечения – м4
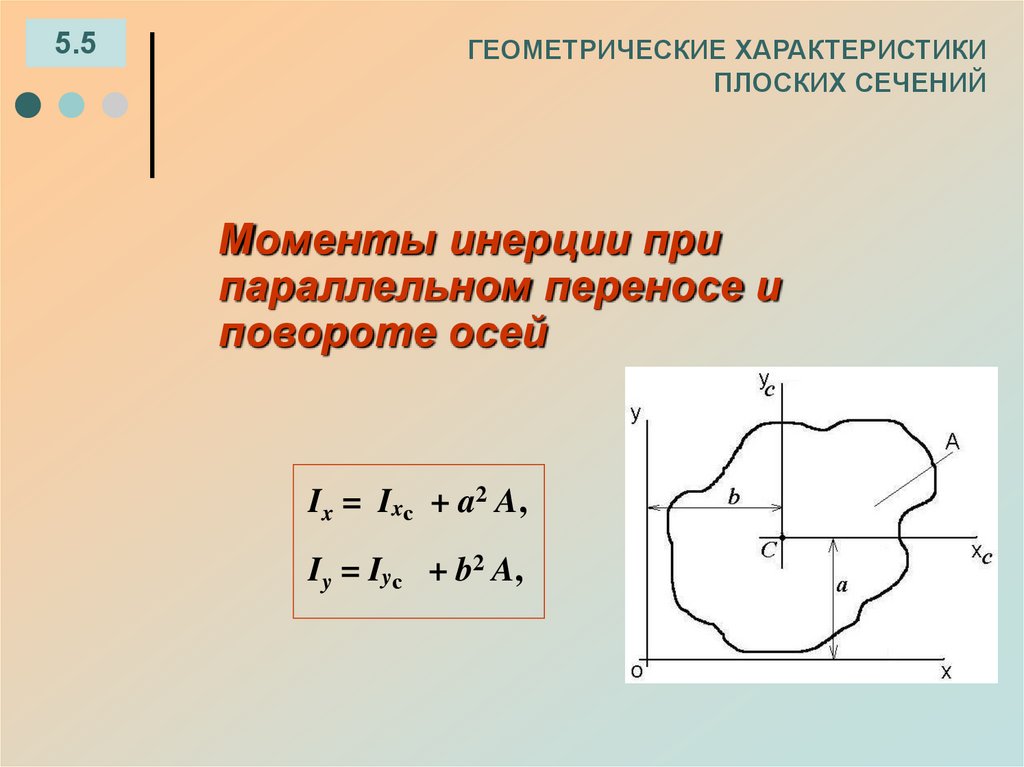
41. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
5.5ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
Моменты инерции при
параллельном переносе и
повороте осей
Ix = Ixс + a2 A,
Iy = Iyс + b2 A,
42. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
5.6ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
Моменты инерции при повороте
осей
Іu = Ix cos2α + Iy sin2α - Ixy sin2α ,
Iν = Ix sin2α + Iy cos2α + Ixy sin2α ,
Iuν =
Ix Iy
2
sin 2α + Ixy cos 2α.
Іu + Iν = Ix + Iy.
43. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
5.7ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
Главные оси и главные моменты инерции
Главные оси сечения - это оси u и v, относительно которых
центробежный момент инерции Іuν = 0, а осевые моменты инерции Іu и
Iν имеют экстремальные значения max или min
tg 2 0
2 I xy
Ix Iy
Главные центральные оси - это
главные оси проходящие через центр тяжести
сечения
Главные моменты инерции
I max
min
Ix Iy
2
1
2
( I x I y )2 4 I xy
2
.
44. ЛЕКЦИЯ 6 План:
6.1МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ПРОСТЕЙШИЕ ВИДЫ ДЕФОРМАЦИИ
Чистый сдвиг. Кручение
ЛЕКЦИЯ 6
План:
6.1. Чистый сдвиг
6.2. Кручение. Эпюры крутящих моментов
6.3. Напряжения при кручении
6.4. Деформации при кручении
6.5. Расчёт вала на прочность и на жёсткость
45. ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
6.2ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
ЧИСТЫЙ СДВИГ - напряженное состояние, при
котором на гранях элемента конструкции возникают только
касательные напряжения
= G· ,
где
- угол сдвига;
G - модуль сдвига,
для стали G = 8 ·104 МПа
Для изотропных материалов :
G = E / [2(1 + )]
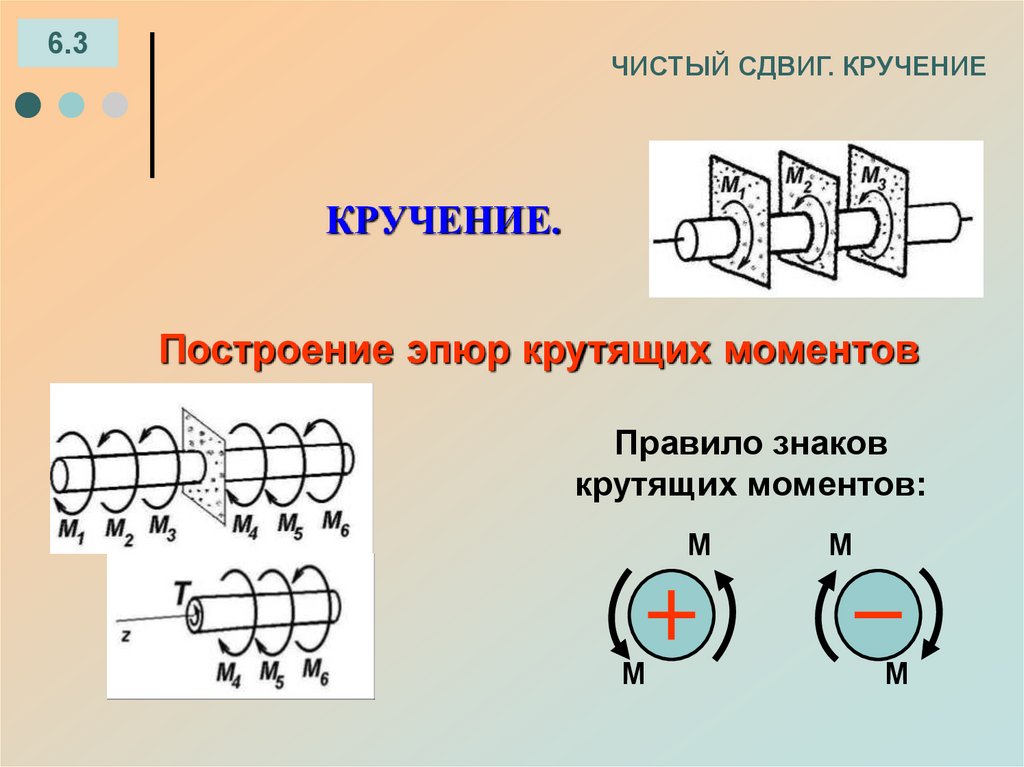
46. ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
6.3ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
КРУЧЕНИЕ.
Построение эпюр крутящих моментов
Правило знаков
крутящих моментов:
М
М
М
М
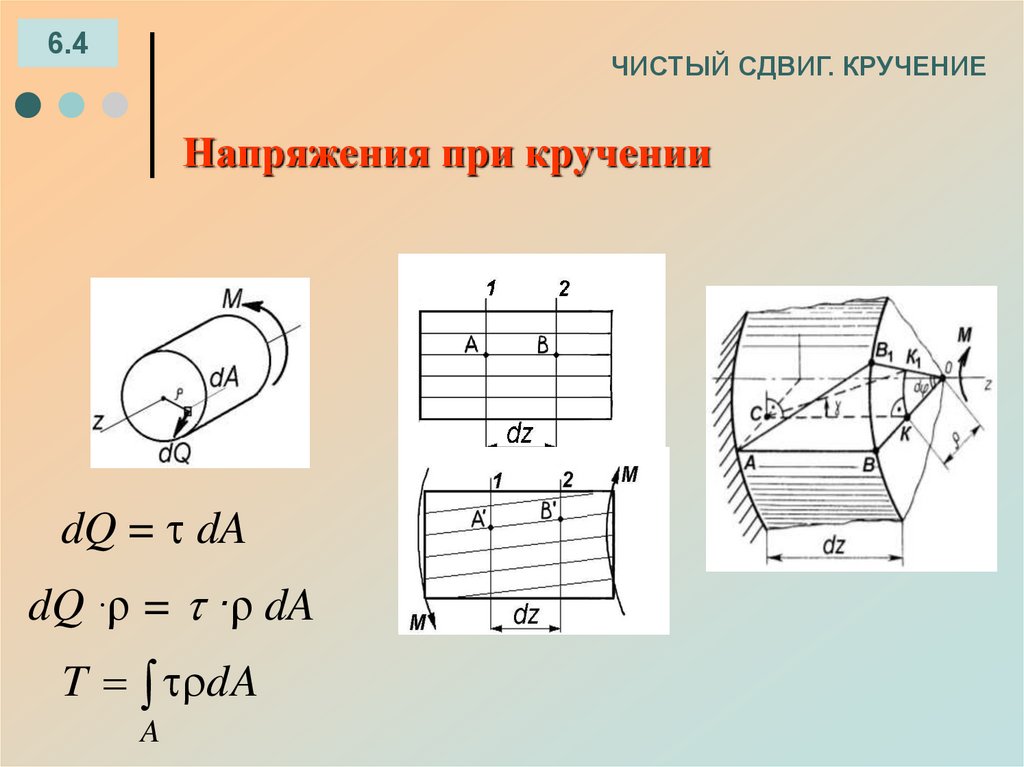
47. ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
6.4ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
Напряжения при кручении
dQ = dA
dQ ·ρ = ·ρ dA
T dA
A
48. ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
6.5ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
Напряжения при кручении
КК dz d
d
dz
по закону Гука: = G·
d
G
dz
d
d T
- относительный
dz угол закручивания,
dz GI
d 2
d
G
dA G
I
dz A
dz
T
I
49. ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
6.6ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
Напряжения при кручении
T
T
max max
I
W
W I / max I / R 2 I / d
Для круглого сечения W = π d3/16 ≈ 0,2 d3
Для сечения в виде кольца
d
d
W = 0,2 D3(1- с4)
D
50. ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
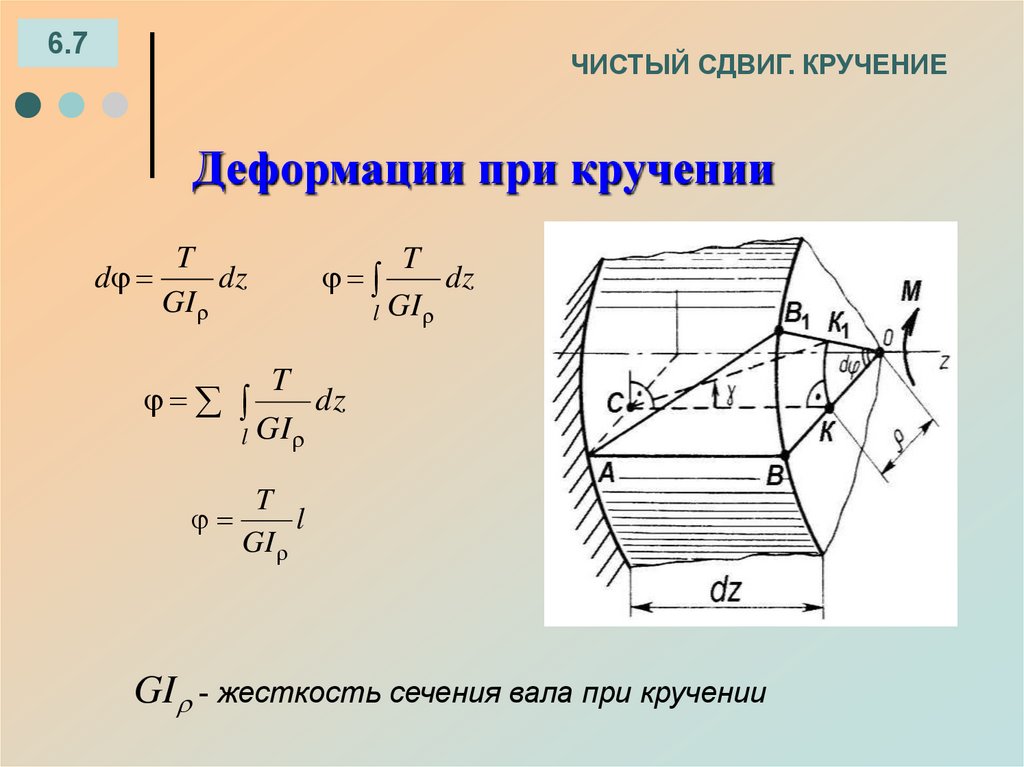
6.7ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
Деформации при кручении
d
T
dz
GI
l GI
T
l GI
T
dz
dz
T
l
GI
GI - жесткость сечения вала при кручении
51. ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
6.8ЧИСТЫЙ СДВИГ. КРУЧЕНИЕ
Расчёт вала на прочность и жёсткость
Условие прочности вала
d 3
Tmax
0,2[ ]
max [ ]
Условие жесткости вала
Tmax
max
[ ]
W
[T ] [ ]W
T
max
[ ]
GI
52. ЛЕКЦИЯ 7 План:
7.1МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ПРОСТЕЙШИЕ ВИДЫ ДЕФОРМАЦИИ
Изгиб
ЛЕКЦИЯ 7
План:
7.1. Общие сведения
7.2. Внутренние силовые факторы при изгибе балки
7.3. Дифференциальные зависимости Журавского
7.4. Внутренние силовые факторы в сечениях рам
53. ИЗГИБ
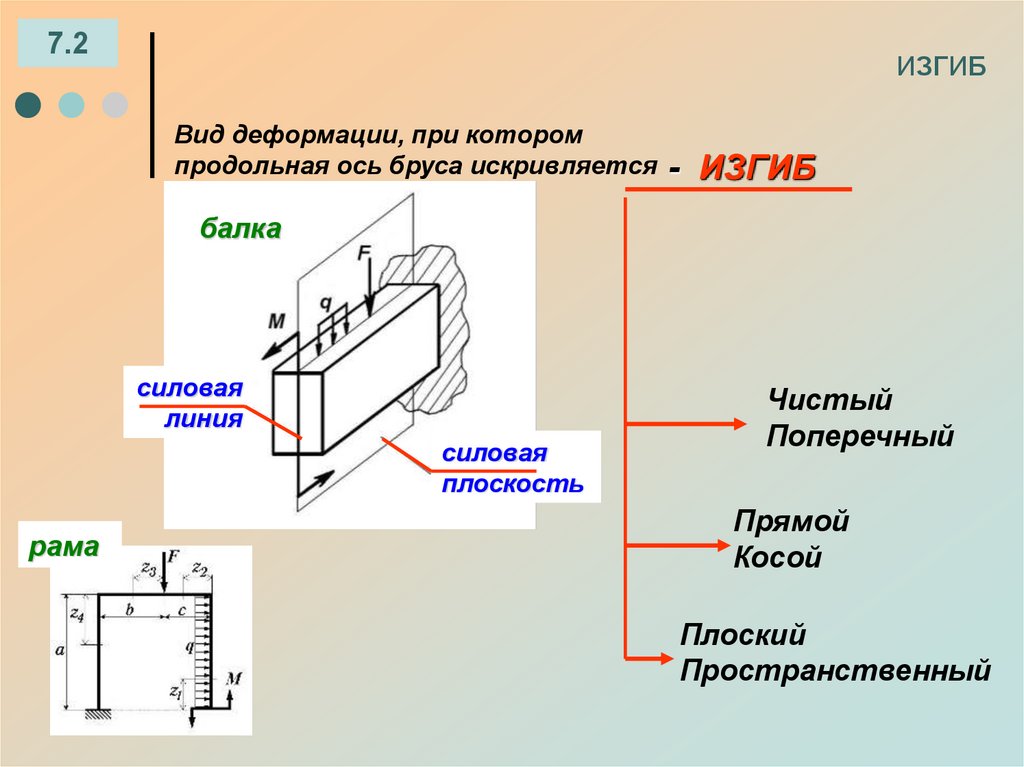
7.2ИЗГИБ
Вид деформации, при котором
продольная ось бруса искривляется -
ИЗГИБ
балка
силовая
линия
силовая
плоскость
рама
Чистый
Поперечный
Прямой
Косой
Плоский
Пространственный
54. ИЗГИБ
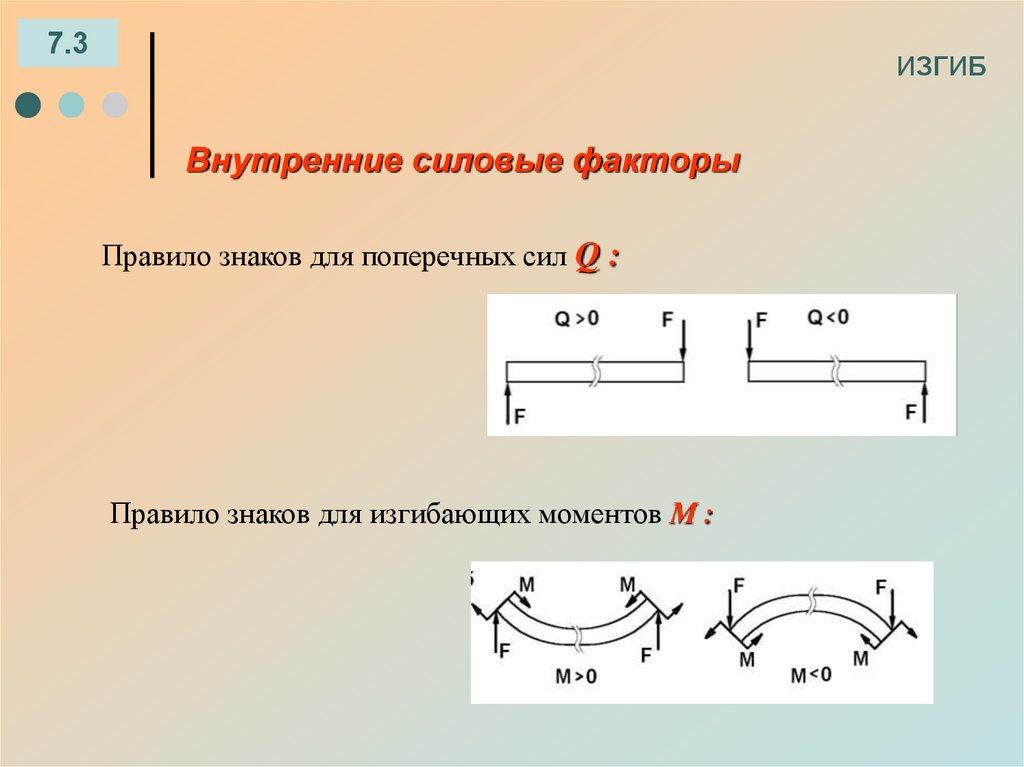
7.3ИЗГИБ
Внутренние силовые факторы
Правило знаков для поперечных сил Q :
Правило знаков для изгибающих моментов М :
55. ИЗГИБ
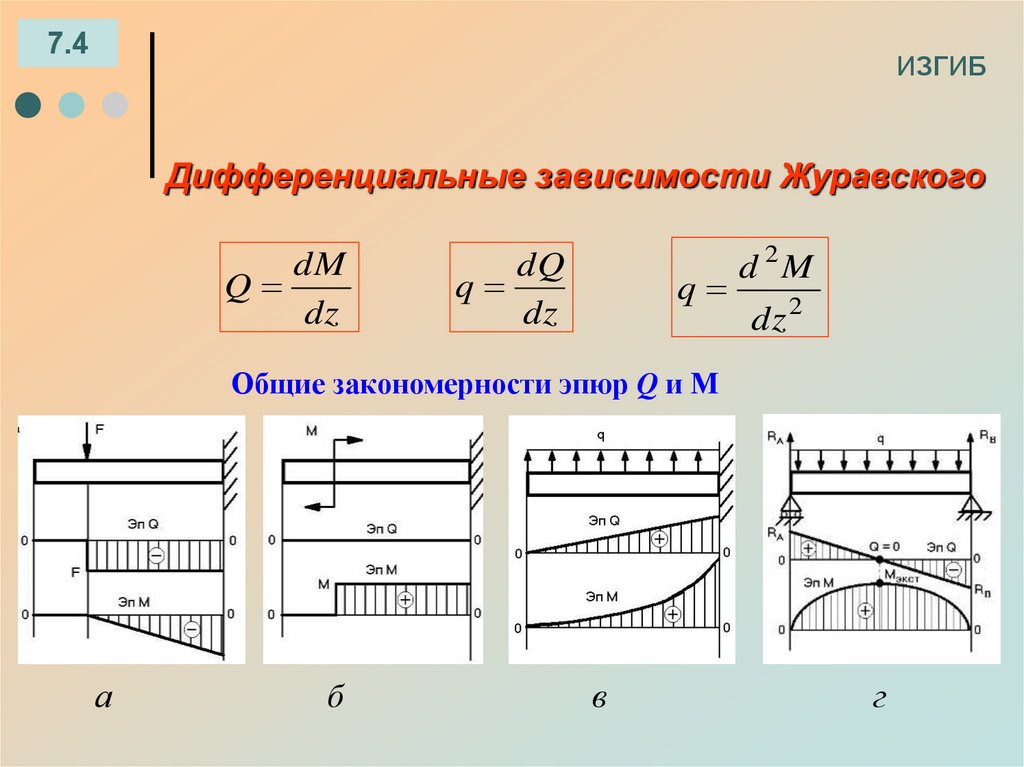
7.4ИЗГИБ
Дифференциальные зависимости Журавского
dM
Q
dz
dQ
q
dz
q
d 2M
dz 2
Общие закономерности эпюр Q и М
а
б
в
г
56. ИЗГИБ
7.5ИЗГИБ
ВНУТРЕННИЕ СИЛОВЫЕ ФАКТОРЫ
В СЕЧЕНИЯХ РАМ
В сечениях стержней рамы кроме изгибающих
моментов M и поперечных сил Q, обычно действуют
еще и продольные силы N.
Границами характерных участков для рамы
- являются также места изменения направления оси
рамы.
При определении знаков внутренних силовых
факторов наблюдателю удобно располагать взгляд как
бы изнутри контура рамы.
При построении этих эпюр положительные
ординаты M, Q и N откладывают с внешней стороны,
а отрицательные – внутрь контура рамы.
57. ЛЕКЦИЯ 8 План:
8.1МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ПРОСТЕЙШИЕ ВИДЫ ДЕФОРМАЦИИ
Изгиб
ЛЕКЦИЯ 8
План:
8.1. Напряжения при чистом изгибе
8.2. Напряжения при плоском поперечном изгибе
58. ИЗГИБ
8.2ИЗГИБ
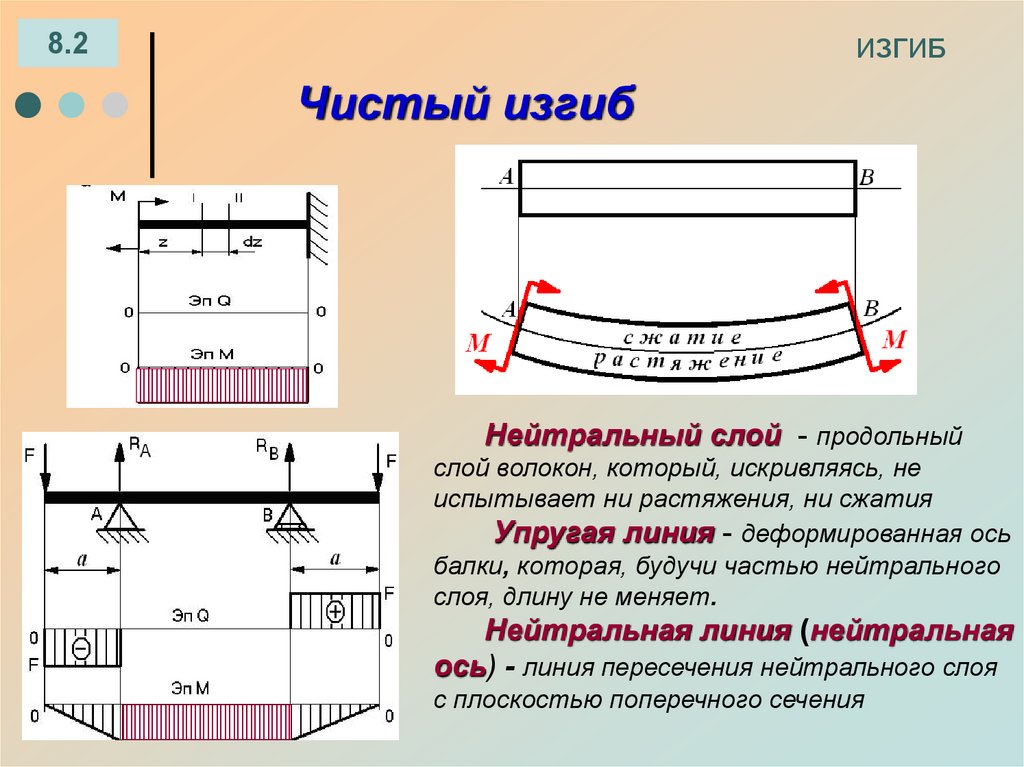
Чистый изгиб
Нейтральный слой - продольный
слой волокон, который, искривляясь, не
испытывает ни растяжения, ни сжатия
Упругая линия - деформированная ось
балки, которая, будучи частью нейтрального
слоя, длину не меняет.
Нейтральная линия (нейтральная
ось) - линия пересечения нейтрального слоя
с плоскостью поперечного сечения
59. ИЗГИБ
8.3ИЗГИБ
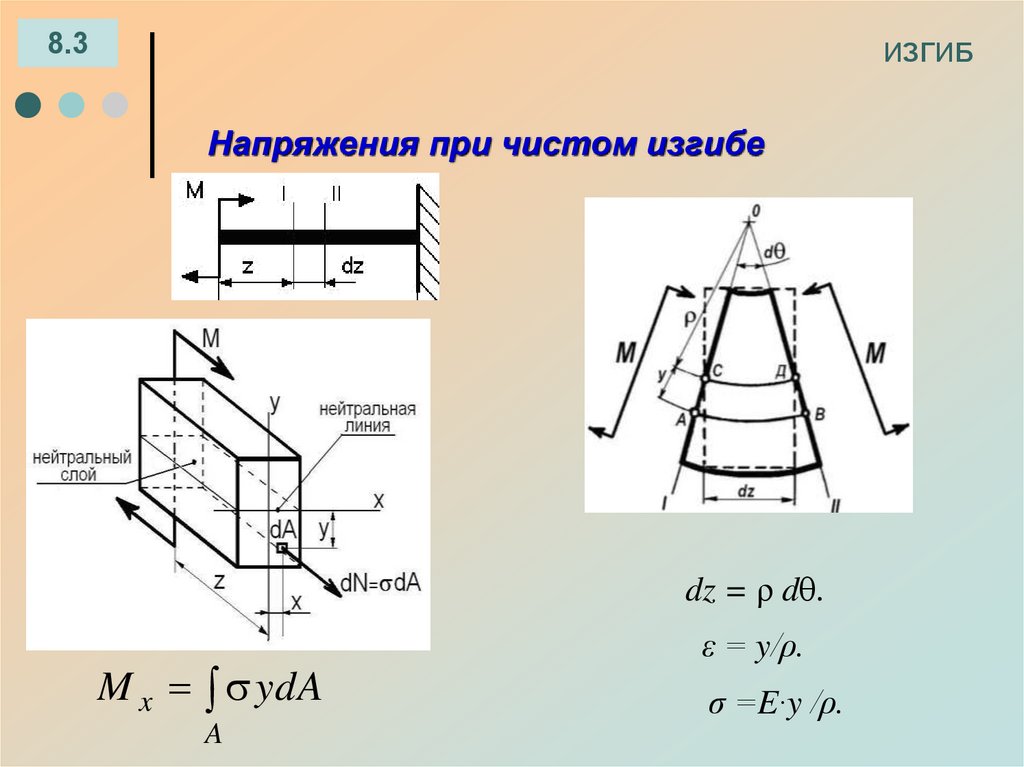
Напряжения при чистом изгибе
dz = ρ d .
M x y dA
A
ε = y/ρ.
σ =E·y /ρ.
60. ИЗГИБ
8.4ИЗГИБ
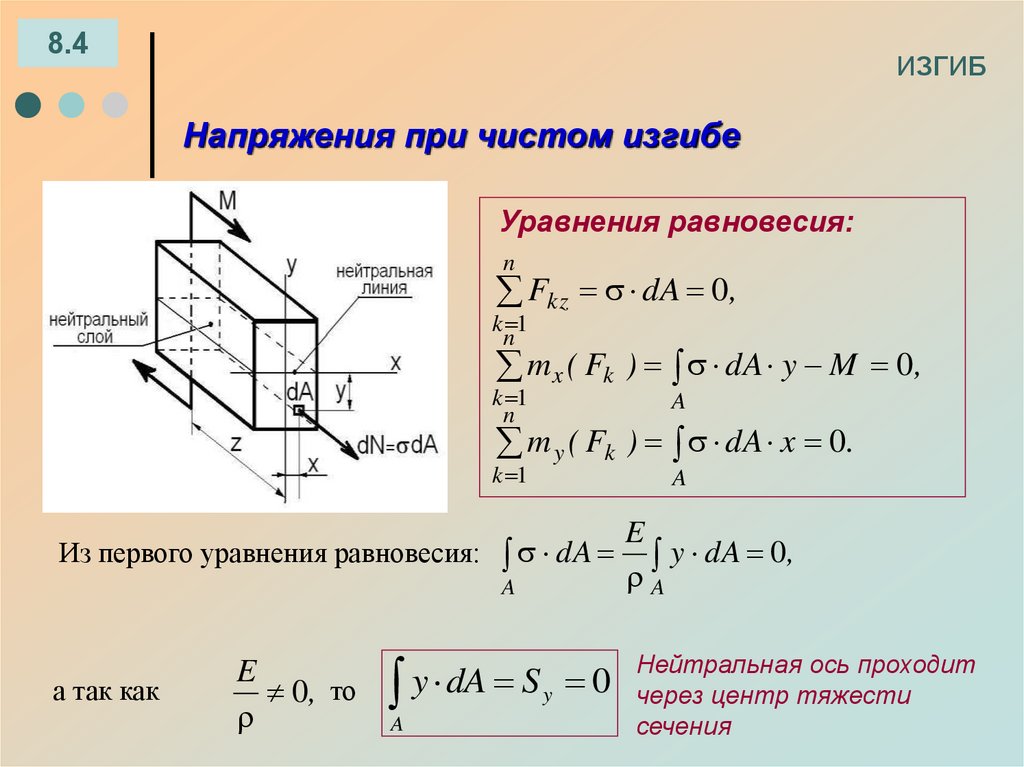
Напряжения при чистом изгибе
Уравнения равновесия:
n
Fkz dA 0,
k 1
n
m x ( Fk ) dA y M 0,
k 1
n
A
k 1
A
m y ( Fk ) dA x 0.
Из первого уравнения равновесия:
dA
A
а так как
E
0, то
y dA S y 0
A
E
y dA 0,
A
Нейтральная ось проходит
через центр тяжести
сечения
61. ИЗГИБ
8.5ИЗГИБ
Напряжения при чистом изгибе
Уравнения равновесия:
n
Fkz dA 0,
k 1
n
Третье из уравнений равновесия
E
dA
x
y x dA 0.
A
A
Так как
E
0,
y x dA I xy 0.
A
m x ( Fk ) dA y M 0,
k 1
n
A
k 1
A
m y ( Fk ) dA x 0.
то
Нейтральная линия совпадает с главной
центральной осью поперечного сечения
балки.
62. ИЗГИБ
8.6ИЗГИБ
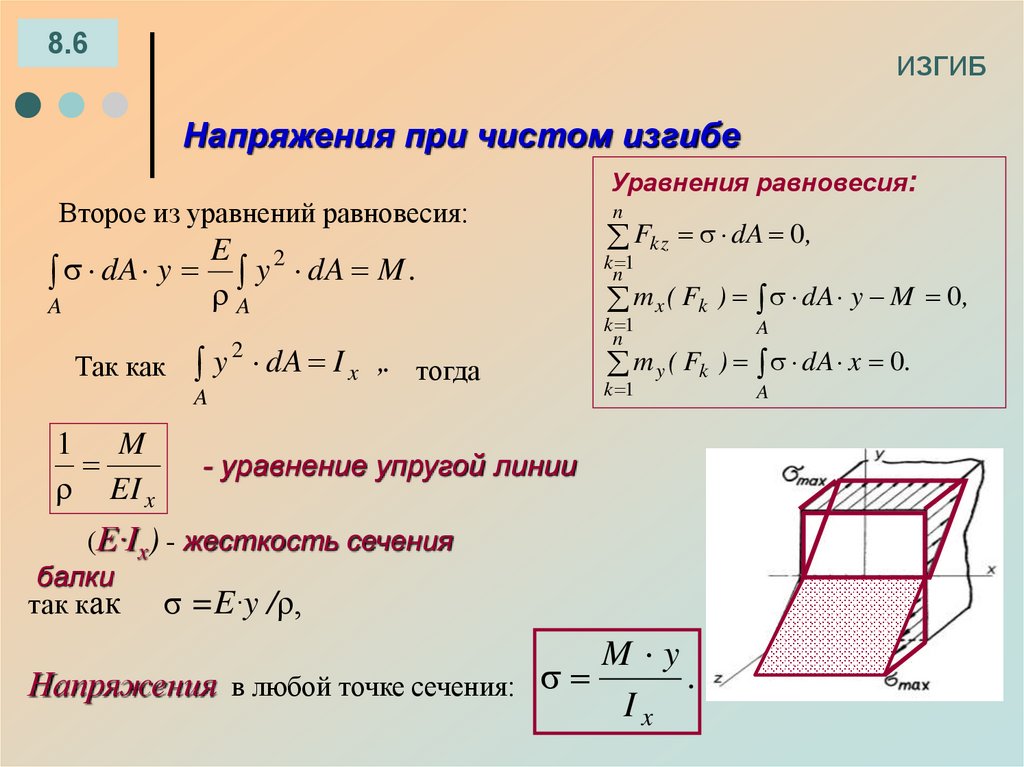
Напряжения при чистом изгибе
Второе из уравнений равновесия:
E 2
dA y y dA M .
A
A
2
y
dA I x ,. тогда
Так как
A
1 M
EI x
Уравнения равновесия:
n
Fkz dA 0,
k 1
n
m x ( Fk ) dA y M 0,
k 1
n
A
k 1
A
m y ( Fk ) dA x 0.
- уравнение упругой линии
(E·Ix) - жесткость сечения
балки
так как σ =E·y /ρ,
M y
.
Напряжения в любой точке сечения:
Ix
63. ИЗГИБ
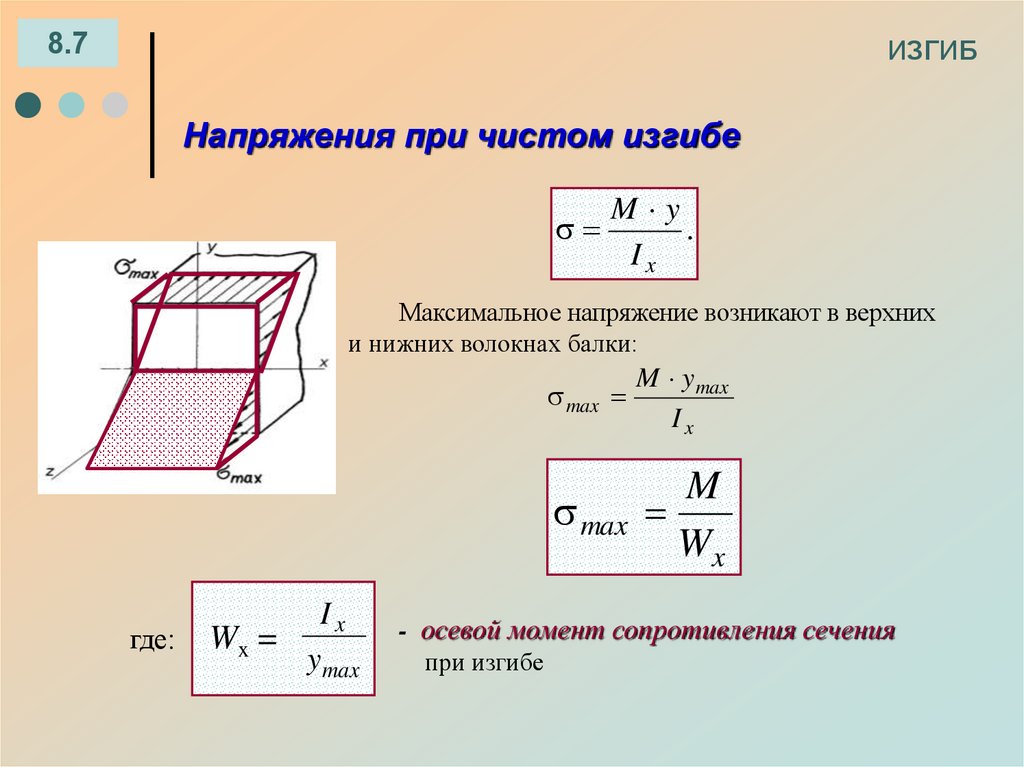
8.7ИЗГИБ
Напряжения при чистом изгибе
M y
.
Ix
Максимальное напряжение возникают в верхних
и нижних волокнах балки:
max
M y max
Ix
M
max
Wx
где:
Ix
Wx =
y max
- осевой момент сопротивления сечения
при изгибе
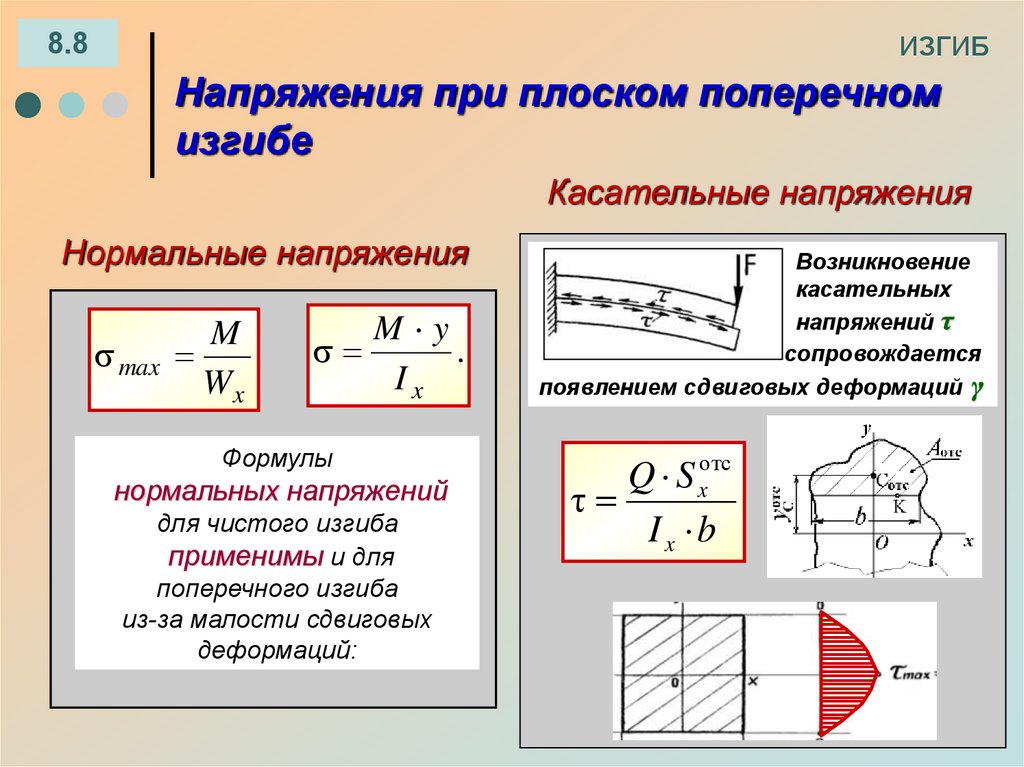
64. ИЗГИБ
8.8Напряжения при плоском поперечном
изгибе
Касательные напряжения
Нормальные напряжения
M
max
Wx
M y
.
Ix
Формулы
нормальных напряжений
для чистого изгиба
применимы и для
поперечного изгиба
из-за малости сдвиговых
деформаций:
Возникновение
касательных
напряжений τ
сопровождается
появлением сдвиговых деформаций γ
Q S xотс
τ
Ix b
65. ЛЕКЦИЯ 9 План:
9.1МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ПРОСТЕЙШИЕ ВИДЫ ДЕФОРМАЦИИ
Изгиб
ЛЕКЦИЯ 9
План:
9.1. Условие прочности при изгибе
9.2. Перемещения при изгибе
66. ИЗГИБ
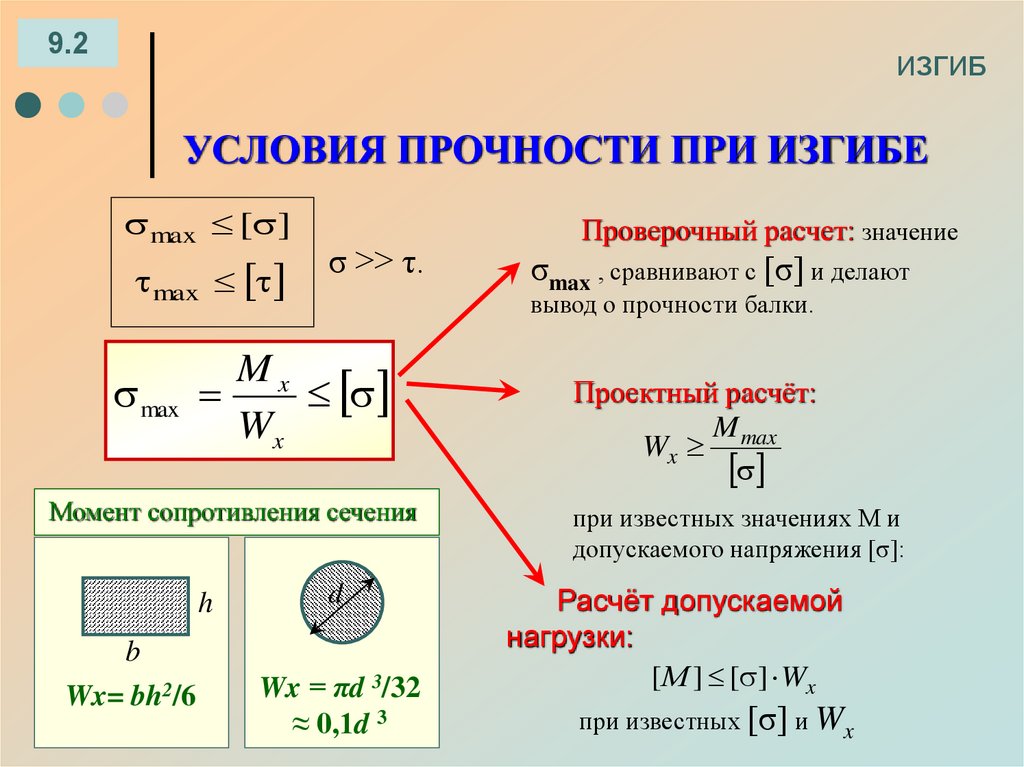
9.2ИЗГИБ
УСЛОВИЯ ПРОЧНОСТИ ПРИ ИЗГИБЕ
max [ ]
max
σ >> τ.
Момент сопротивления сечения
b
Wx= bh2/6
σmax , сравнивают с [σ] и делают
вывод о прочности балки.
Mx
max
Wx
h
Проверочный расчет: значение
d
Wx = πd 3/32
≈ 0,1d 3
Проектный расчёт:
M max
Wx
при известных значениях М и
допускаемого напряжения [σ]:
Расчёт допускаемой
нагрузки:
[ М ] [ ] Wx
при известных [σ] и Wx
67. ИЗГИБ
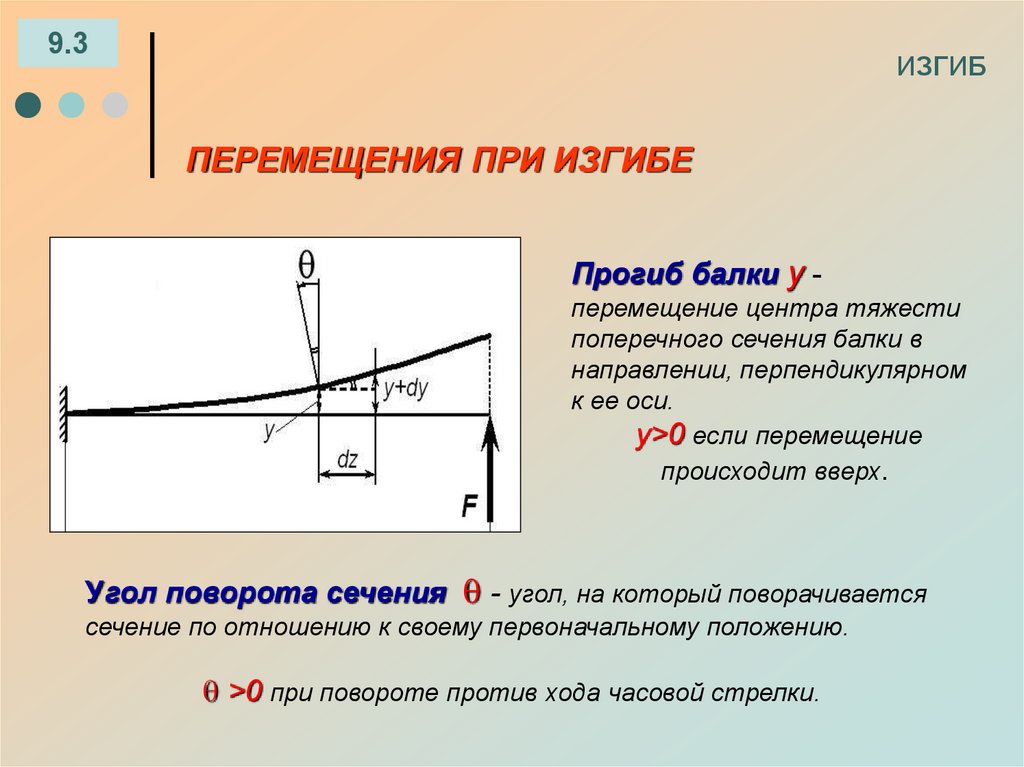
9.3ИЗГИБ
ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ
Прогиб балки у перемещение центра тяжести
поперечного сечения балки в
направлении, перпендикулярном
к ее оси.
у>0 если перемещение
происходит вверх.
Угол поворота сечения - угол, на который поворачивается
сечение по отношению к своему первоначальному положению.
>0 при повороте против хода часовой стрелки.
68. ИЗГИБ
9.4ИЗГИБ
ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ
Прогибы у и углы поворота
dy
связаны между собой: tgθ
y' θ
dz
1
y
.
3
2
1 y 2
y
M
2 32
EI x
1 y
Так как
y
1
, то
2
M
y
EI x
1 М
ЕI x
дифференциальное
уравнение упругой
линии
приближенное
дифференциальное
уравнение упругой линии
69. ИЗГИБ
9.5ИЗГИБ
ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ
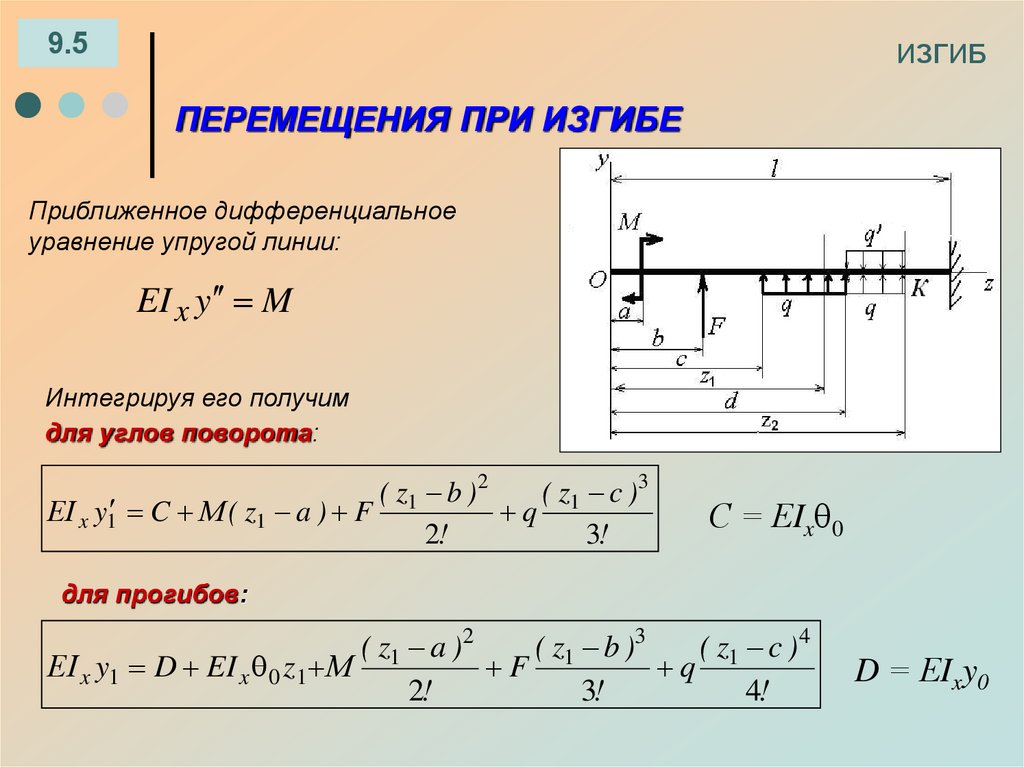
Приближенное дифференциальное
уравнение упругой линии:
EI x y M
Интегрируя его получим
для углов поворота:
( z1 b )2
( z1 c )3
ЕI x y1 C М ( z1 a ) F
q
2!
3!
С = ЕIx 0
для прогибов:
( z1 a )2
( z1 b )3
( z1 c )4
ЕI x y1 D EI x 0 z1 М
F
q
2!
3!
4!
D = ЕIxy0
70. В общем виде УНИВЕРСАЛЬНЫЕ УРАВНЕНИЯ
9.6ИЗГИБ
ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ
В общем виде УНИВЕРСАЛЬНЫЕ УРАВНЕНИЯ
для прогибов:
( z lq )
( z lM )2
( z lF )3
EI x у EI x y0 EJ x 0 z M
F
q
2!
3!
4!
4
для углов поворота :
( z lq )
( z lM )
( z l F )2
EI x EI x 0 M
F
q
1!
2!
3!
3
Начальные параметры находят из условий закрепления балки.
для консольной балки в заделке : y0 = 0, 0 = 0,
для балки на шарнирных опорах в опорных точках: yA = 0, yB = 0.
71. ИЗГИБ
9.7ИЗГИБ
ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ
Метод Мора:
В точке с искомым перемещением конструкцию
нагружают единичной силой, которая совершает
работу на возможном (искомом) перемещении.
Порядок определения перемещений :
1.
Строят «вспомогательную систему» и нагружают ее единичной
нагрузкой в точке с искомым перемещением .
2. Для каждого участка
системы записывают выражения изгибающих
.
моментов от приложенной нагрузки Мf и от единичной нагрузки - М1.
3. По всем участкам системы вычисляют и суммируют интегралы Мора,
получая в результате искомое перемещение :
M f M1
EI x
dz
72. ИЗГИБ
9.8ИЗГИБ
ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ
Правило Верещагина (графоаналитический способ)
Af – площадь эпюры изгибающего
момента Мf от заданной
нагрузки;
A f yc
yc – ордината эпюры от
единичной
EI x
нагрузки под центром
тяжести
эпюры Мf ;
EIx – жесткость сечения участка
балки.
Вычисления производятся по участкам,
на каждом из которых
прямолинейная эпюра должна быть без переломов.
Сложная эпюра Мf разбивается на простые фигуры.
Площадь каждой фигуры умножается на ординату под ее
центром тяжести
73. Раздел - 8. СЛОЖНОЕ СОПРОТИВЛЕНИЕ
МЕХАНИКАСопротивление материалов
Раздел - 8. СЛОЖНОЕ СОПРОТИВЛЕНИЕ
Напряжено-деформированное
состояние в точке
Сложное сопротивление бруса
ЛЕКЦИЯ 10
ЛЕКЦИЯ 11
ЛЕКЦИЯ 12
74. ЛЕКЦИЯ 10 План:
10.1МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
СЛОЖНОЕ СОПРОТИВЛЕНИЕ
Теория напряженно-деформированного
состояния
ЛЕКЦИЯ 10
План:
10.1. Напряженное состояние в точке
10.2. Обобщенный закон Гука
10.3. Теории прочности
75. СЛОЖНОЕ СОПРОТИВЛЕНИЕ
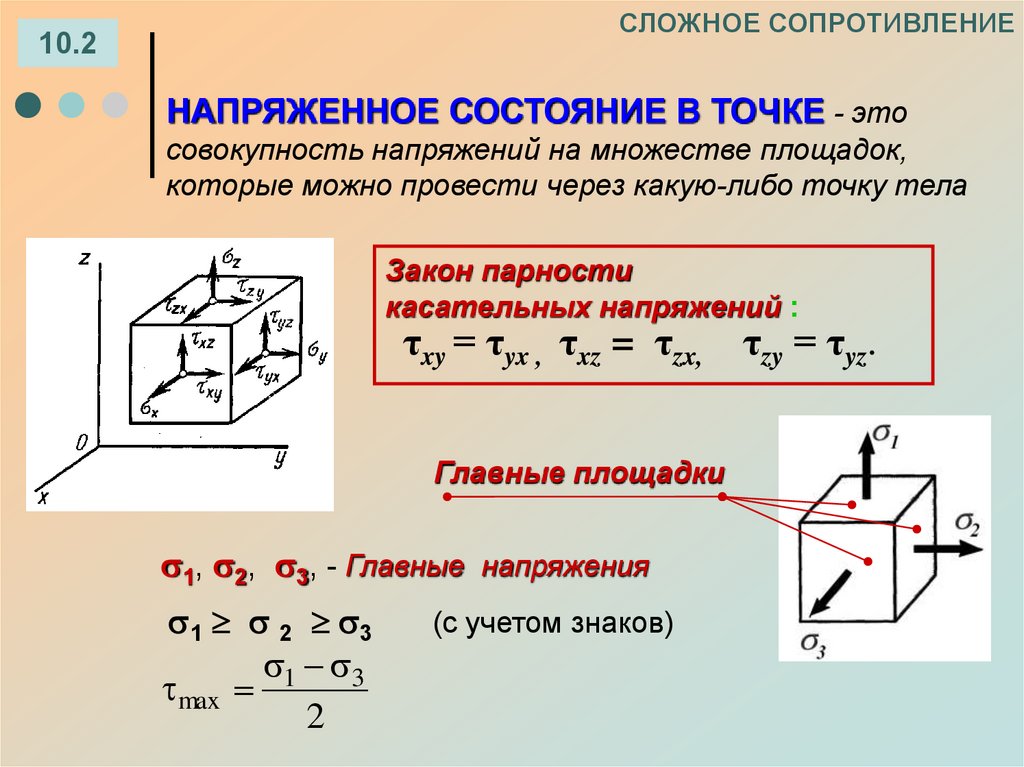
10.2НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ - это
совокупность напряжений на множестве площадок,
которые можно провести через какую-либо точку тела
Закон парности
касательных напряжений :
τxy = τyx , τxz = τzx, τzy = τyz.
Главные площадки
1, 2, 3, - Главные напряжения
1 2 3
1 3
max
2
(с учетом знаков)
76. СЛОЖНОЕ СОПРОТИВЛЕНИЕ
10.3СЛОЖНОЕ СОПРОТИВЛЕНИЕ
НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ
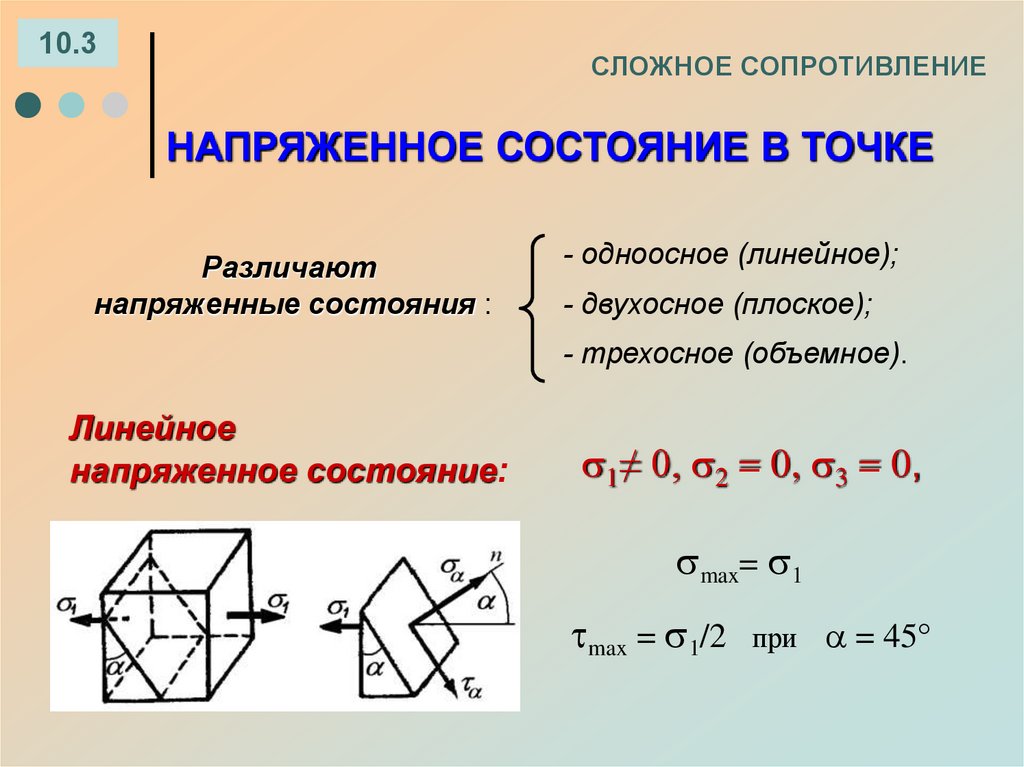
Различают
напряженные состояния :
- одноосное (линейное);
- двухосное (плоское);
- трехосное (объемное).
Линейное
напряженное состояние:
1≠ 0, 2 = 0, 3 = 0,
max= 1
max = 1/2 при = 45
77. СЛОЖНОЕ СОПРОТИВЛЕНИЕ
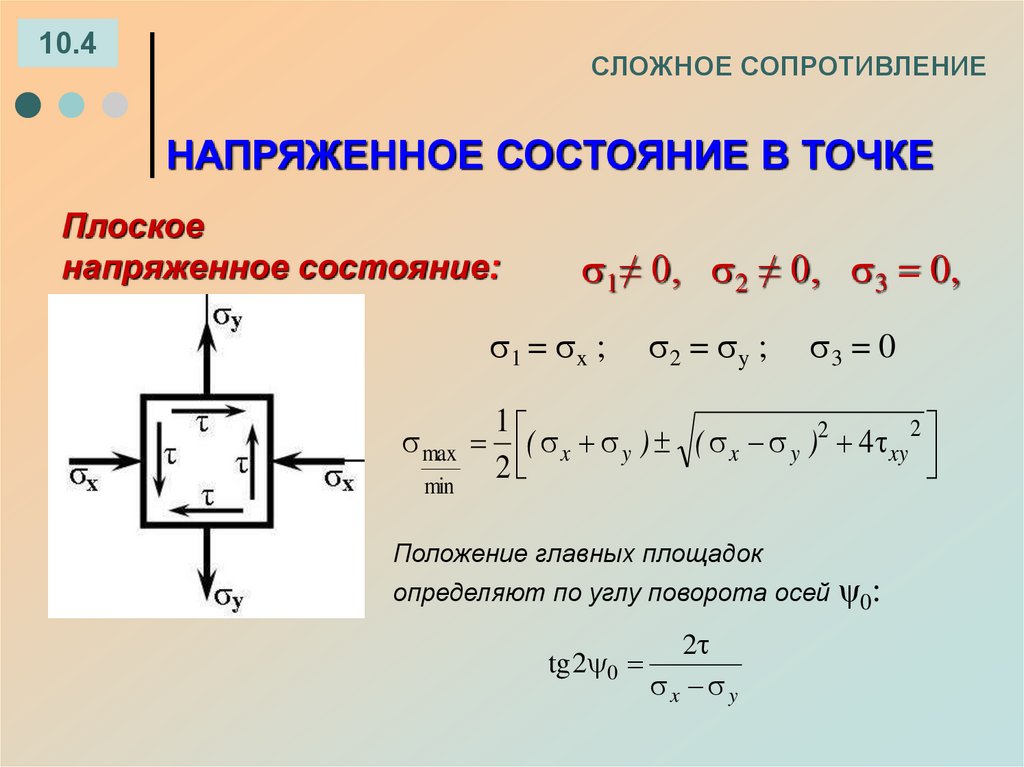
10.4СЛОЖНОЕ СОПРОТИВЛЕНИЕ
НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ
Плоское
напряженное состояние:
1≠ 0, 2 ≠ 0, 3 = 0,
1 = x ;
2 = y ;
3 = 0
1
max ( x y ) ( x y )2 4 xy 2
2
min
Положение главных площадок
определяют по углу поворота осей ψ0:
2
tg 2 0
x y
78. СЛОЖНОЕ СОПРОТИВЛЕНИЕ
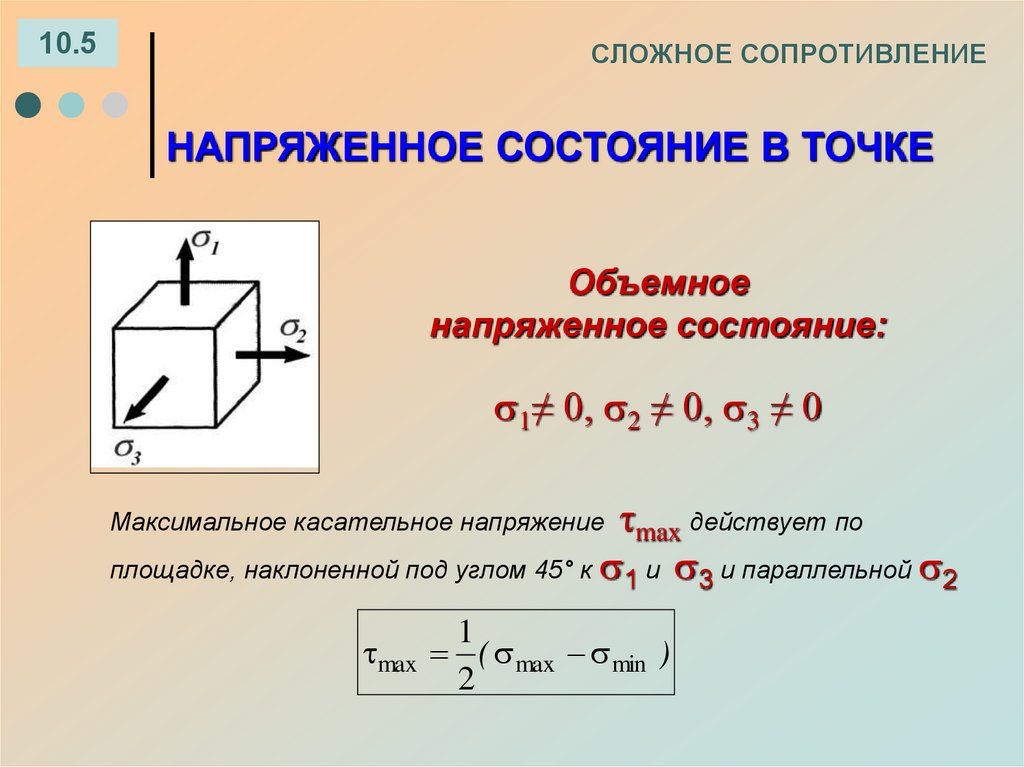
10.5СЛОЖНОЕ СОПРОТИВЛЕНИЕ
НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ
Объемное
напряженное состояние:
1≠ 0, 2 ≠ 0, 3 ≠ 0
Максимальное касательное напряжение τmax действует по
площадке, наклоненной под углом 45° к 1 и 3 и параллельной 2
1
max ( max min )
2
79.
10.6СЛОЖНОЕ СОПРОТИВЛЕНИЕ
ОБОБЩЕННЫЙ ЗАКОН ГУКА
Направле
-ние
деформации
x
y
z
Относительные деформации
ε и ε' от действия нормальных
напряжений
σx
x
E
x
E
x
E
σy
y
E
y
E
y
E
σz
z
E
z
E
z
E
Сложив все деформации одного
направления, получают
обобщенный закон Гука
1
x x ( y z )
E
1
y y ( x z )
E
1
z z ( x y )
E
относительное изменение объема при деформации
v x y z ( 1 2 )( x y z ) / E
80. СЛОЖНОЕ СОПРОТИВЛЕНИЕ
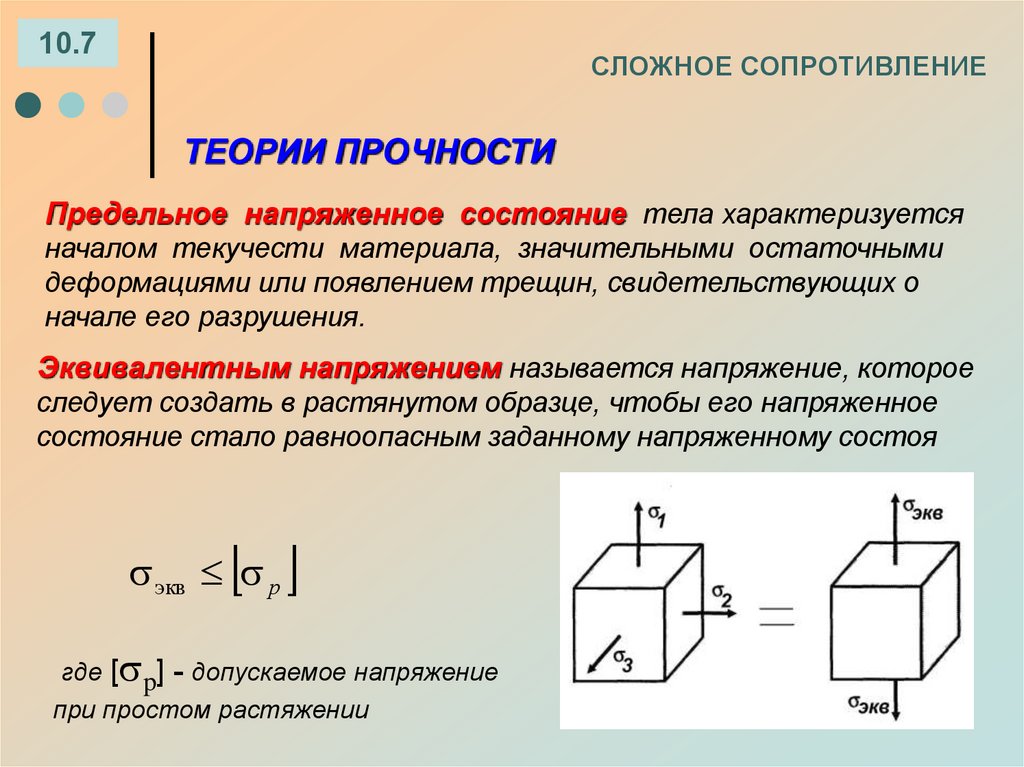
10.7СЛОЖНОЕ СОПРОТИВЛЕНИЕ
ТЕОРИИ ПРОЧНОСТИ
Предельное напряженное состояние тела характеризуется
началом текучести материала, значительными остаточными
деформациями или появлением трещин, свидетельствующих о
начале его разрушения.
Эквивалентным напряжением называется напряжение, которое
следует создать в растянутом образце, чтобы его напряженное
состояние стало равноопасным заданному напряженному состоя
экв р
где [ p] - допускаемое напряжение
при простом растяжении
81. СЛОЖНОЕ СОПРОТИВЛЕНИЕ
10.8СЛОЖНОЕ СОПРОТИВЛЕНИЕ
ТЕОРИИ ПРОЧНОСТИ
1. Теория наибольших нормальных напряжений
(первая гипотеза прочности)
экв ma x [ ]
2. Теория наибольших относительных удлинений
(вторая гипотеза прочности)
3. Теория наибольших касательных напряжений
(третья гипотеза прочности) экв ( z ) 4 zy [ ]
2
2
4. Теория энергии формоизменения
(энергетическая теория) экв ( z )2 3 2 [ ]
5. Теория прочности Мора
(пятая гипотеза прочности) экв 1 k 3
82. ЛЕКЦИЯ 11 План:
11.1МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
СЛОЖНОЕ СОПРОТИВЛЕНИЕ
Сложное сопротивление бруса
ЛЕКЦИЯ 11
План:
11.1. Понятие сложного сопротивления
11.2. Косой изгиб
83. Сложное сопротивление
11.2Сложное сопротивление
Сложное сопротивление - вид нагружения,
при котором в поперечных сечениях бруса одновременно
возникает несколько внутренних силовых факторов.
Случаи сложного сопротивления:
- одноосное напряженное состояние, или приближенное
к
нему (косой изгиб, внецентренное
растяжение
и
-плоское
напряженное
состояние (изгиб с кручением,
сжатие, или
изгиб
с растяжением
);
растяжение
сжатие
с кручением,
растяжение или сжатие с изгибом).
84. ИЗГИБ
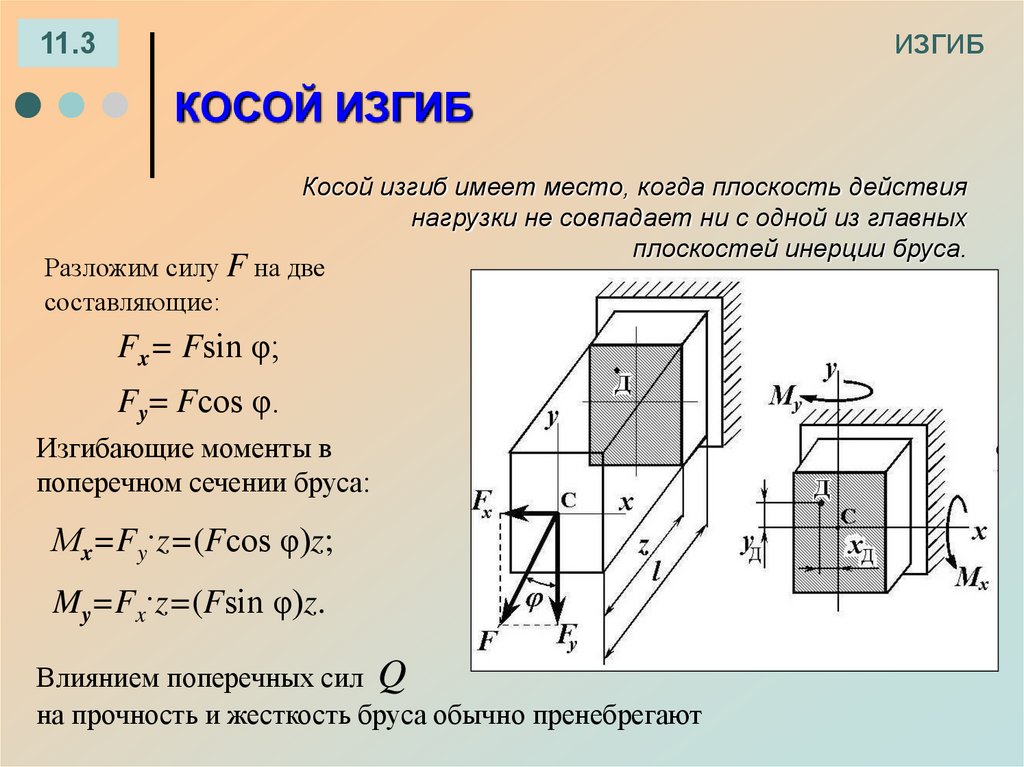
11.3КОСОЙ ИЗГИБ
Косой изгиб имеет место, когда плоскость действия
нагрузки не совпадает ни с одной из главных
плоскостей инерции бруса.
Разложим силу F на две
составляющие:
Fx= Fsin φ;
Fy= Fcos φ.
Изгибающие моменты в
поперечном сечении бруса:
Мx=Fy·z=(Fcos φ)z;
My=Fx·z=(Fsin φ)z.
Влиянием поперечных сил Q
на прочность и жесткость бруса обычно пренебрегают
85. ИЗГИБ
11.4ИЗГИБ
КОСОЙ ИЗГИБ
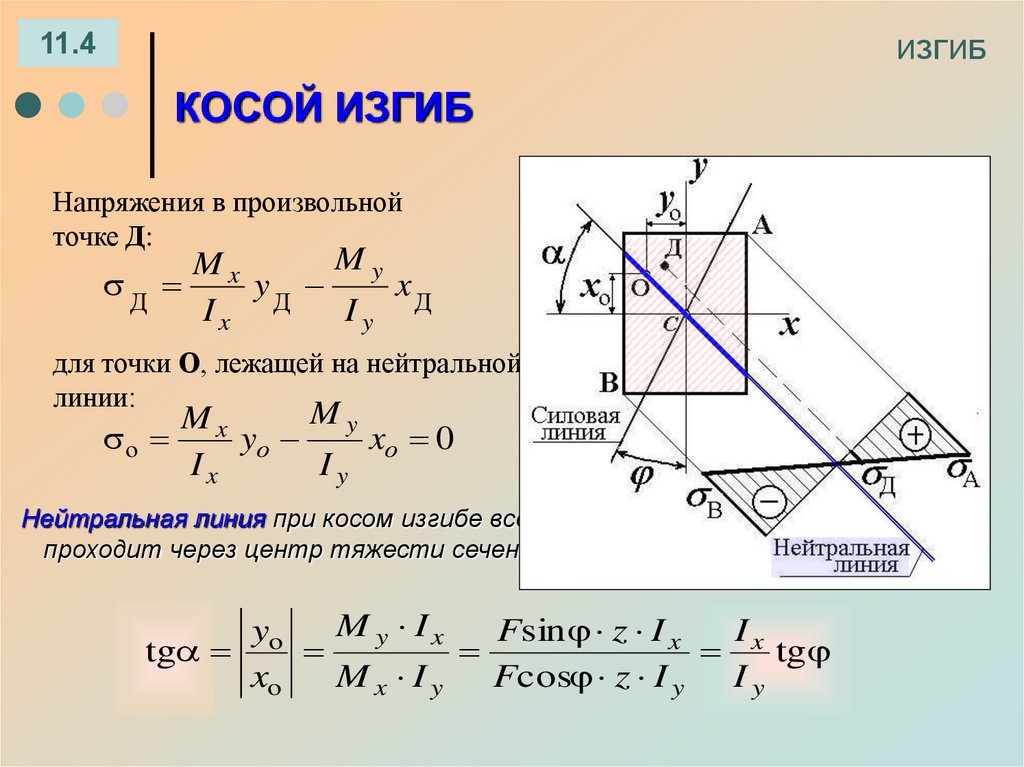
Напряжения в произвольной
точке Д:
My
Mx
Д
yД
xД
Ix
Iy
для точки О, лежащей на нейтральной
линии:
My
Mx
о
yо
xо 0
Ix
Iy
Нейтральная линия при косом изгибе всегда
проходит через центр тяжести сечения
M y Ix
yo
Fsin z I x
Ix
tg
tg
xo
M x I y Fcos z I y I y
86. ИЗГИБ
11.5ИЗГИБ
КОСОЙ ИЗГИБ
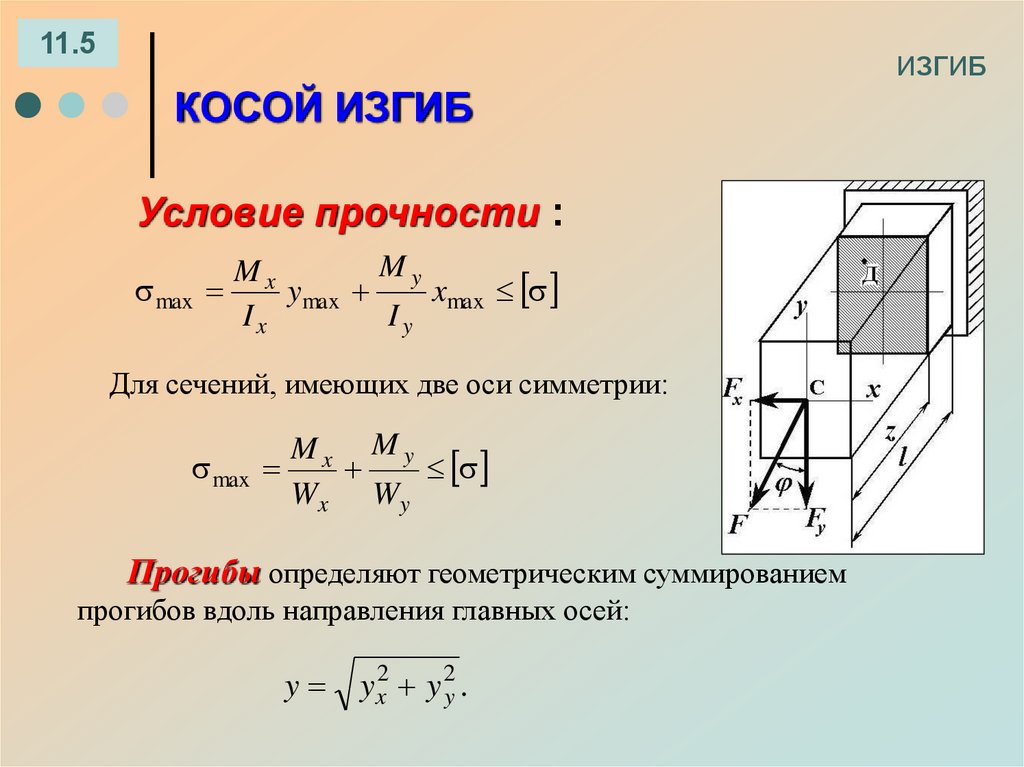
Условие прочности :
My
Mx
max
ymax
xmax
Ix
Iy
Для сечений, имеющих две оси симметрии:
Mx My
max
Wx W y
Прогибы определяют геометрическим суммированием
прогибов вдоль направления главных осей:
y
y x2 y 2y .
87. ЛЕКЦИЯ 12 План:
12.1МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
СЛОЖНОЕ СОПРОТИВЛЕНИЕ
Сложное сопротивление бруса
ЛЕКЦИЯ 12
План:
12.1. Изгиб с растяжением (сжатием)
12.2. Внецентренное растяжение или сжатие
12.3. Кручение с изгибом
88. Сложное сопротивление
12.2ИЗГИБ С РАСТЯЖЕНИЕМ (СЖАТИЕМ)
Внутренние усилия :
N= Fz,
Qx= Fx, Мх = Fy z,
Qy= Fy , My = Fx z
Напряжение в произвольно
выбранной точке Д :
My
N Mx
yд
xд
A Ix
Iy
Условие прочности для сечений с двумя осями симметрии :
N Mx My
max
A Wx Wy
89. Сложное сопротивление
12.3ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ
(СЖАТИЕ)
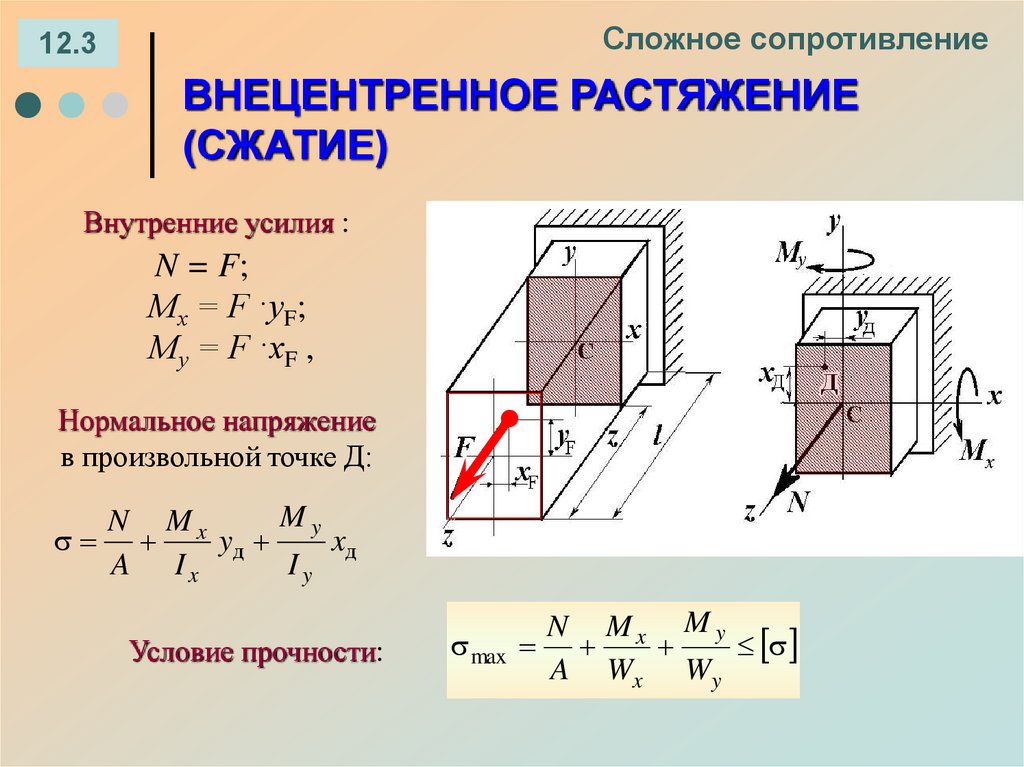
Внутренние усилия :
N = F;
Мх = F ·yF;
Му = F ·xF ,
Нормальное напряжение
в произвольной точке Д:
My
N Mx
yд
xд
A Ix
Iy
Условие прочности:
N Mx My
max
A Wx Wy
90. Сложное сопротивление
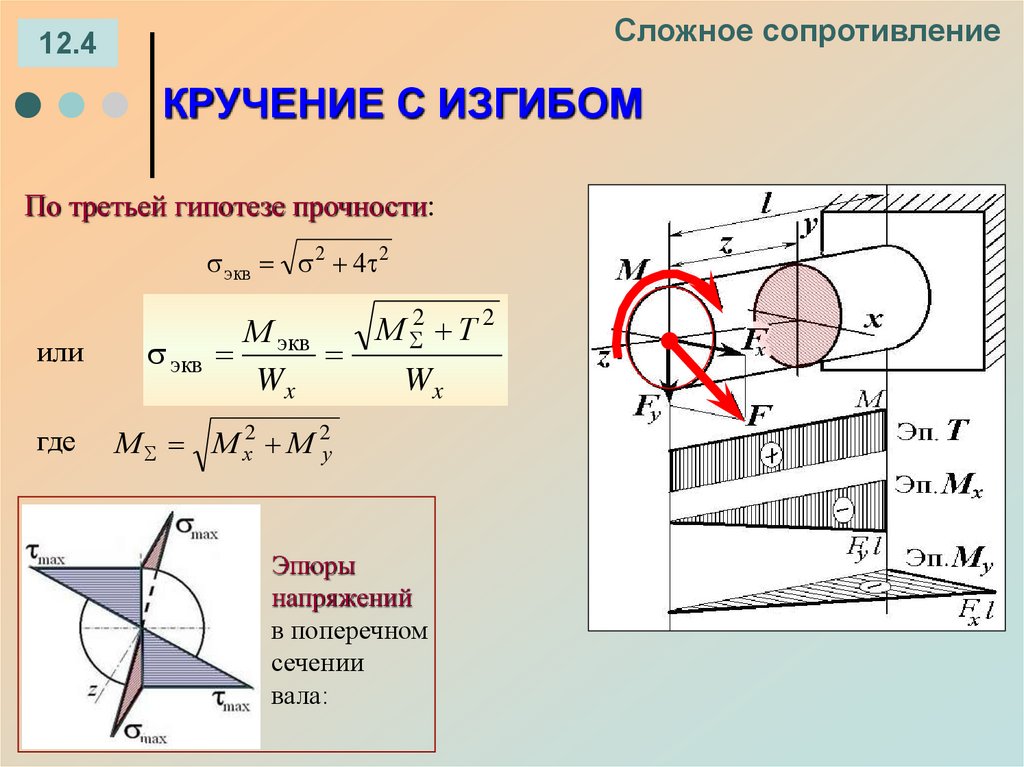
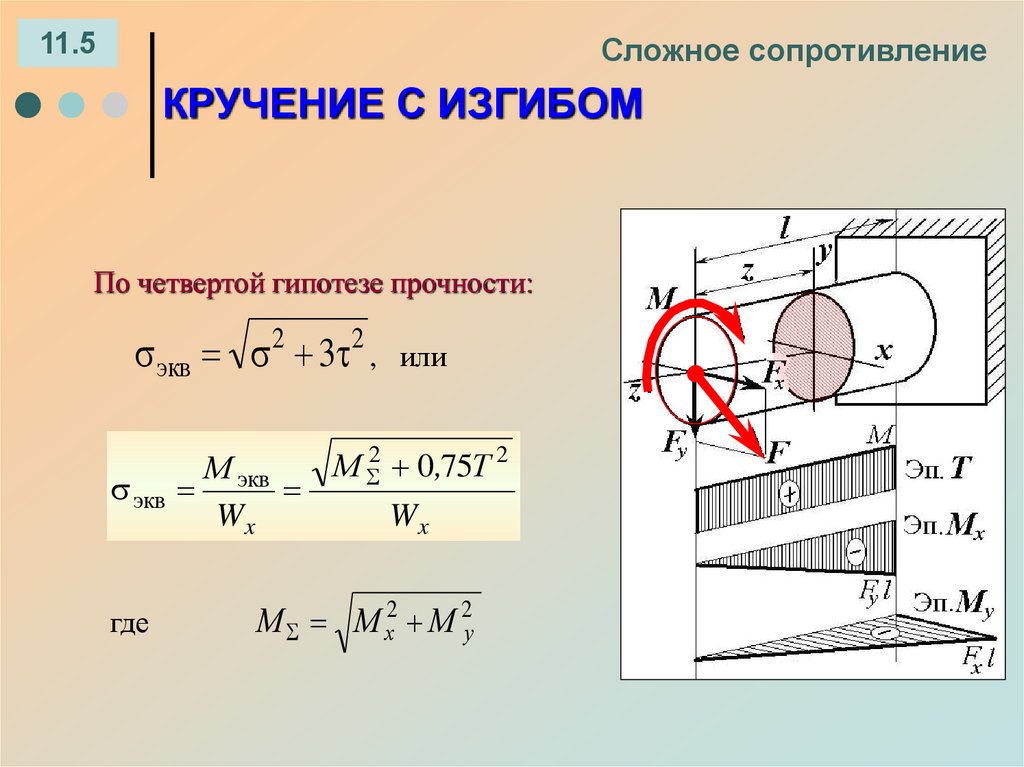
12.4КРУЧЕНИЕ С ИЗГИБОМ
По третьей гипотезе прочности:
экв 2 4 2
или
М экв
экв
Wx
где
М М х2 М 2у
М 2 Т 2
Wx
Эпюры
напряжений
в поперечном
сечении
вала:
91. Сложное сопротивление
11.5Сложное сопротивление
КРУЧЕНИЕ С ИЗГИБОМ
По четвертой гипотезе прочности:
экв 2 3 2 , или
М 2 0 ,75Т 2
М экв
экв
Wx
Wx
где
М М х2 М 2у
92. Раздел – 9. ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ И ДИНАМИЧЕСКИХ НАПРЯЖЕНИЯХ
МЕХАНИКАСопротивление материалов
Раздел – 9. ПРОЧНОСТЬ ПРИ
ПЕРЕМЕННЫХ И ДИНАМИЧЕСКИХ
НАПРЯЖЕНИЯХ
Прочность при переменных
напряжениях
Прочность при ударе
ЛЕКЦИЯ 13
ЛЕКЦИЯ 14
ЛЕКЦИЯ 15
93. ЛЕКЦИЯ 13 План:
13.1МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ И
ДИНАМИЧЕСКИХ НАПРЯЖЕНИЯХ
Расчеты на прочность при переменных
напряжениях
ЛЕКЦИЯ 13
План:
13.1. Явление усталости
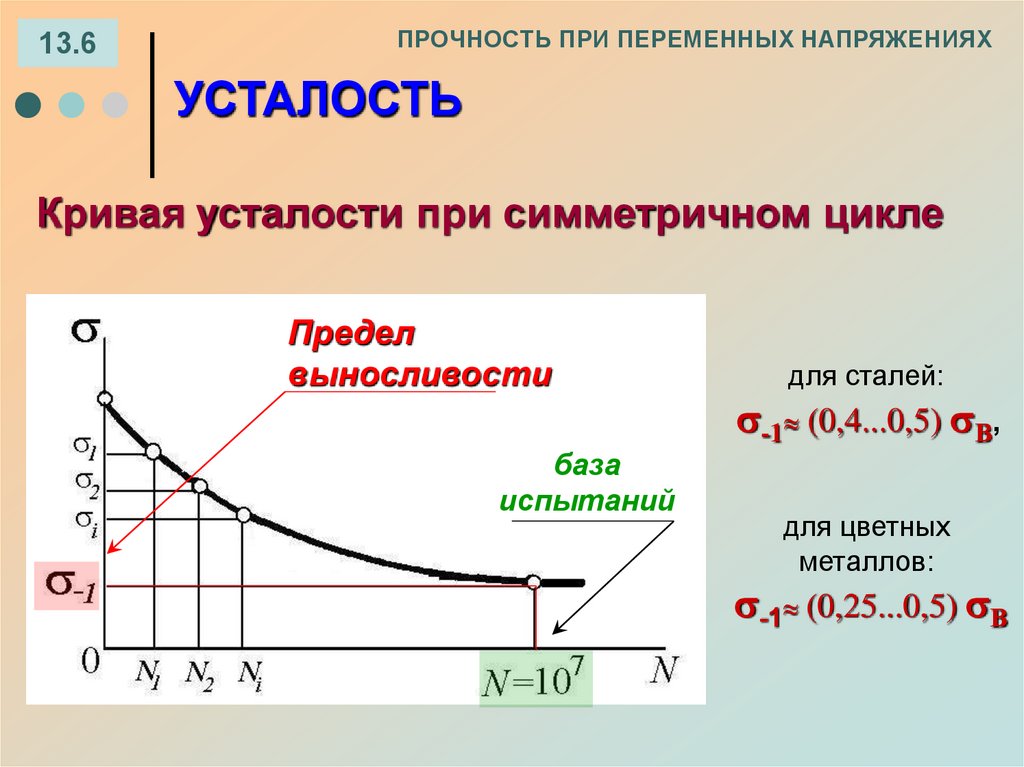
13.2. Кривая усталости при симметричном цикле
94. ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
13.2УСТАЛОСТЬ - процесс постепенного
накопления повреждений в материале под действием
переменных напряжений, приводящий к изменению его
свойств, образованию трещин, их развитию и
разрушению.
Усталостное разрушение – разрушение, происходящее при
напряжениях, значительно меньших предела прочности σВ, а
иногда даже и предела пропорциональности σпц.
Зона А - область распространения
трещины
Зона Б - зона разрыва
Вид усталостного излома
95.
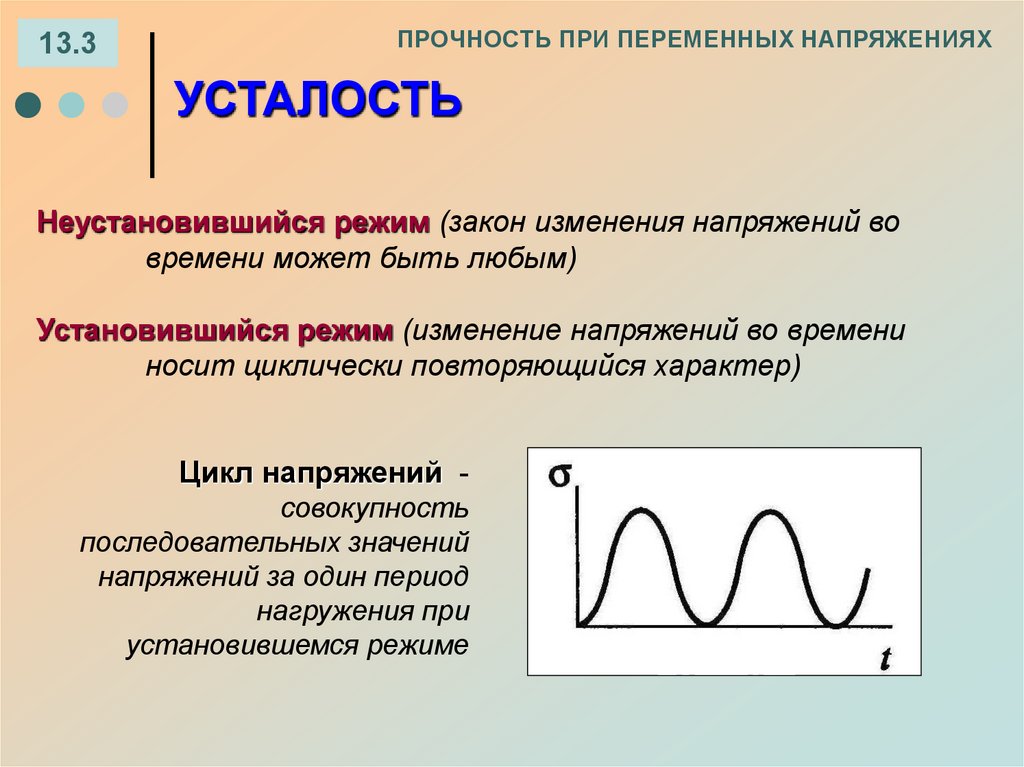
13.3ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
УСТАЛОСТЬ
Неустановившийся режим (закон изменения напряжений во
времени может быть любым)
Установившийся режим (изменение напряжений во времени
носит циклически повторяющийся характер)
Цикл напряжений совокупность
последовательных значений
напряжений за один период
нагружения при
установившемся режиме
96.
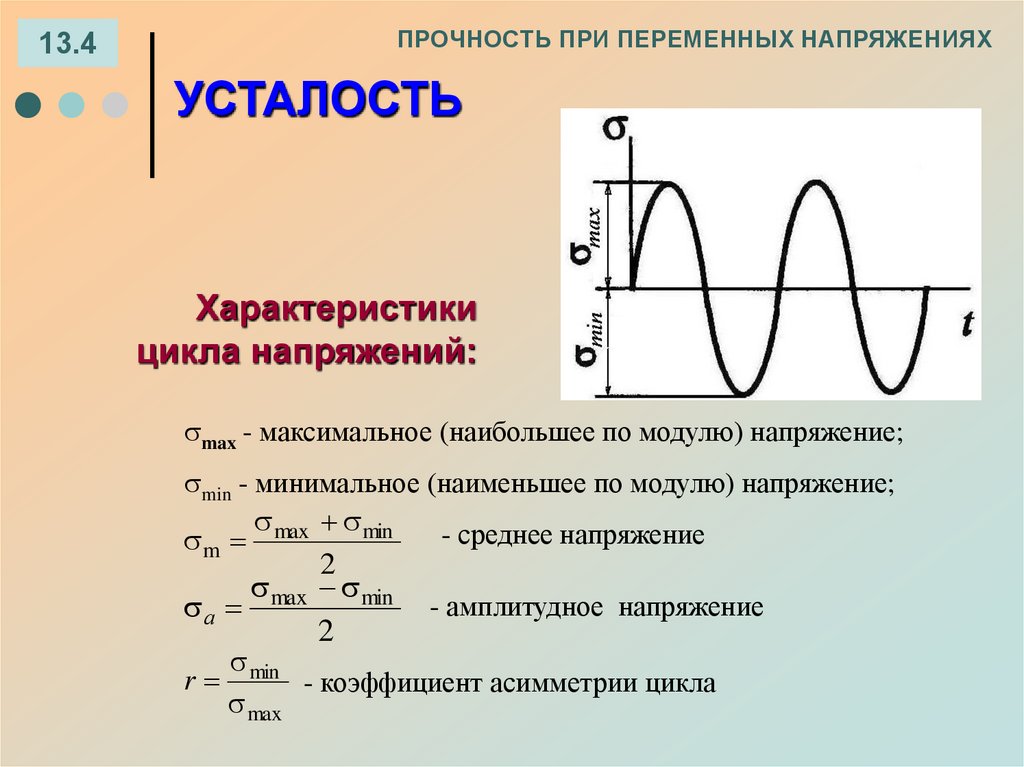
ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ13.4
УСТАЛОСТЬ
Характеристики
цикла напряжений:
max - максимальное (наибольшее по модулю) напряжение;
min - минимальное (наименьшее по модулю) напряжение;
max min
- среднее напряжение
2
max min
- амплитудное напряжение
а
2
min
r
- коэффициент асимметрии цикла
max
m
97.
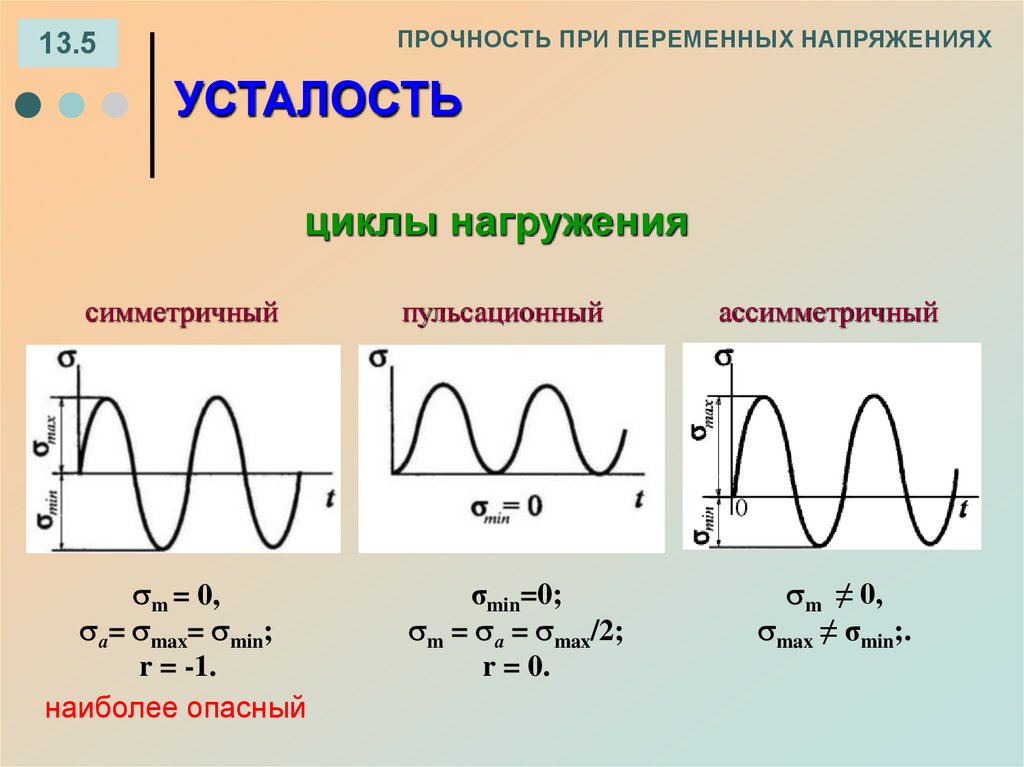
ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ13.5
УСТАЛОСТЬ
циклы нагружения
симметричный
пульсационный
ассимметричный
m = 0,
а= max= min;
r = -1.
наиболее опасный
σmin=0;
m = а = max/2;
r = 0.
m ≠ 0,
max ≠ σmin;.
98.
13.6ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
УСТАЛОСТЬ
Кривая усталости при симметричном цикле
Предел
выносливости
база
испытаний
для сталей:
-1 (0,4...0,5) В,
для цветных
металлов:
-1 (0,25...0,5) В
99. ЛЕКЦИЯ 14 План:
14.1МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ И
ДИНАМИЧЕСКИХ НАПРЯЖЕНИЯХ
Расчеты на прочность при переменных
напряжениях
ЛЕКЦИЯ 14
План:
14.1 Факторы, влияющие на предел выносливости.
14.2 Расчеты конструкций на усталость
100.
ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ14.2
ФАКТОРЫ, ВЛИЯЮЩИЕ
НА ПРЕДЕЛ ВЫНОСЛИВОСТИ
концентрация напряжений,
масштабный фактор,
состояние поверхности,
внешняя среда
101.
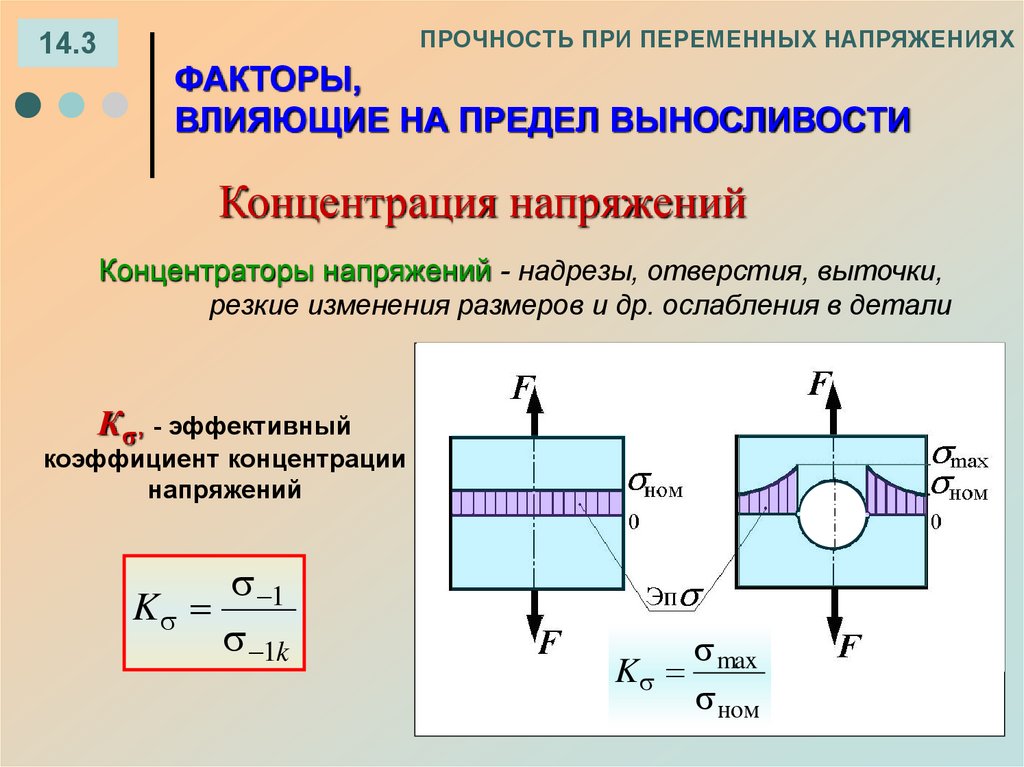
14.3ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
ФАКТОРЫ,
ВЛИЯЮЩИЕ НА ПРЕДЕЛ ВЫНОСЛИВОСТИ
Концентрация напряжений
Концентраторы напряжений - надрезы, отверстия, выточки,
резкие изменения размеров и др. ослабления в детали
Кσ, - эффективный
коэффициент концентрации
напряжений
1
K
1k
max
K
ном
102.
ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ14.4
ФАКТОРЫ,
ВЛИЯЮЩИЕ НА ПРЕДЕЛ ВЫНОСЛИВОСТИ
Масштабный фактор
статистический фактор (высокая вероятность появления
дефектных зон - раковин, неметаллических включений, микротрещин);
технологический фактор (способ обработки детали в
процессе ее изготовления);
производственный фактор (ухудшение качества материала
с увеличением объема детали).
- масштабный коэффициент
1
о
1
Предел выносливости материала в гладком
образце диаметром d
Предел выносливости того же материала в
стандартном образце диаметром do = 6...10 мм
103.
14.5ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ
ФАКТОРЫ,
ВЛИЯЮЩИЕ НА ПРЕДЕЛ ВЫНОСЛИВОСТИ
Состояние поверхности детали
- коэффициент состояния поверхности (для шлифованной
неупрочненной поверхности = 1)
Способ повышения σ-1 - поверхностное упрочнение детали
(наклеп, ХТО, закалка ТВЧ и др.),
Внешняя среда
Коррозия металлов (в поверхностных слоях возникают трещины
коррозионной усталости)
Способ повышения σ-1 - защита от коррозии (антикоррозионные
покрытия, окраска).
104.
ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ14.6
РАСЧЕТЫ КОНСТРУКЦИЙ НА УСТАЛОСТЬ
Условие усталостной прочности :
n
n n
n 2 n 2
n
[n] = 1,5 – 4.
n - коэффициент запаса усталостной прочности,
n
n
1
K
a m
1
K
a m
а
M
Wx
m 0
T
а m
2W
105. ЛЕКЦИЯ 15 План:
15.1МЕХАНИКА
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ И
ДИНАМИЧЕСКИХ НАПРЯЖЕНИЯХ
Прочность при ударе
ЛЕКЦИЯ 15
План:
15.1 Ударная нагрузка
15.2. Динамический коэффициент
15.3. Расчеты на прочность при динамическом нагружении
106. ПРОЧНОСТЬ ПРИ УДАРЕ
15.2ПРОЧНОСТЬ ПРИ УДАРЕ
Ударная нагрузка
Ударная нагрузка - всякая быстроменяющаяся нагрузка.
Гипотезы теории удара:
Удар считают неупругим;
Ударяемое тело имеет одну степень свободы и вся масса
тела сосредоточена в точке удара;
Ударяемая конструкция считается идеально упругой;
Вся кинетическая энергия ударяющего тела преобразуется
в потенциальную энергию упругой деформации ударяемой
конструкции.
Потенциальная энергия статической упругой
деформации растянутого стержня :
N 2l EA( l ) 2
U
2 EA
2l
107.
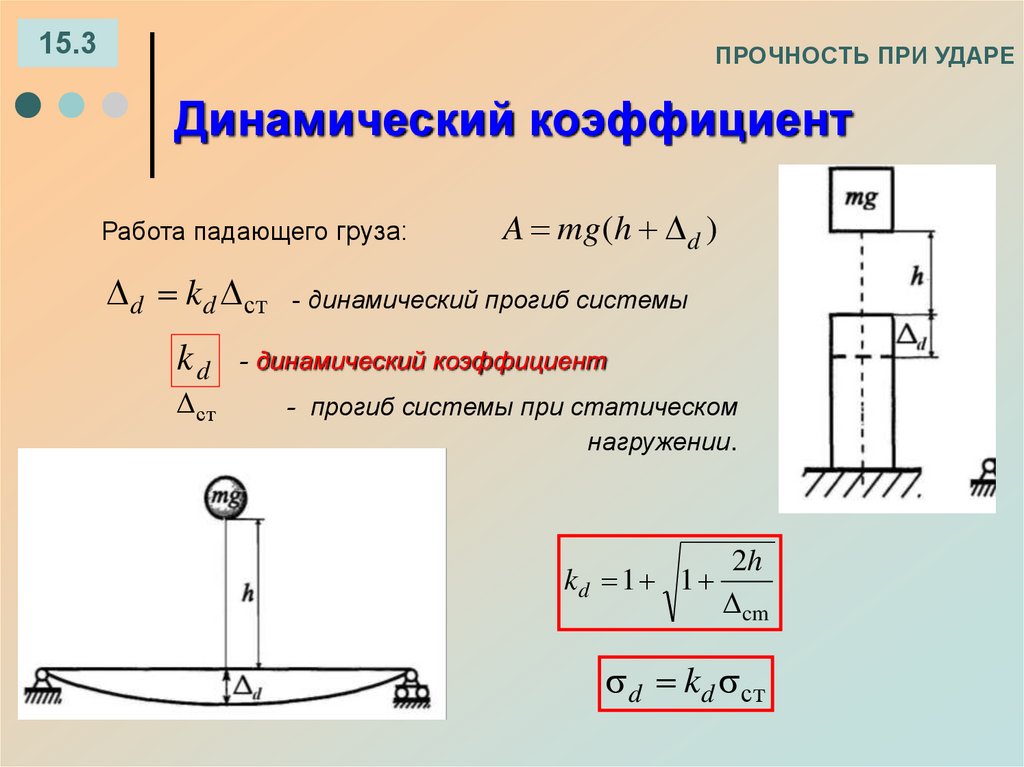
15.3ПРОЧНОСТЬ ПРИ УДАРЕ
Динамический коэффициент
Работа падающего груза:
A mg (h d )
d kd ст - динамический прогиб системы
kd
ст
- динамический коэффициент
- прогиб системы при статическом
нагружении.
kd 1 1
2h
cm
d kd ст
108.
ПРОЧНОСТЬ ПРИ УДАРЕ15.4
Расчеты на прочность при
динамическом нагружении
Частные случаи удара:
1. Внезапное динамическое приложение нагрузки
При h = 0
тогда
2h
kd 1 1
2
cm
d 2 ст
d 2 ст
2. Высота падения значительно больше статической
деформации
При h >> ст
kd
2h
cm
109. Раздел –10. УСТОЙЧИВОСТЬ
МЕХАНИКАСопротивление материалов
Раздел –10. УСТОЙЧИВОСТЬ
Устойчивость сжатых стержней
ЛЕКЦИЯ 16
ЛЕКЦИЯ 17
110. ЛЕКЦИЯ 16 План:
МЕХАНИКА16.1
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
УСТОЙЧИВОСТЬ
Устойчивость сжатых стержней
ЛЕКЦИЯ 16
План:
16.1. Понятие об устойчивости первоначальной формы
равновесия
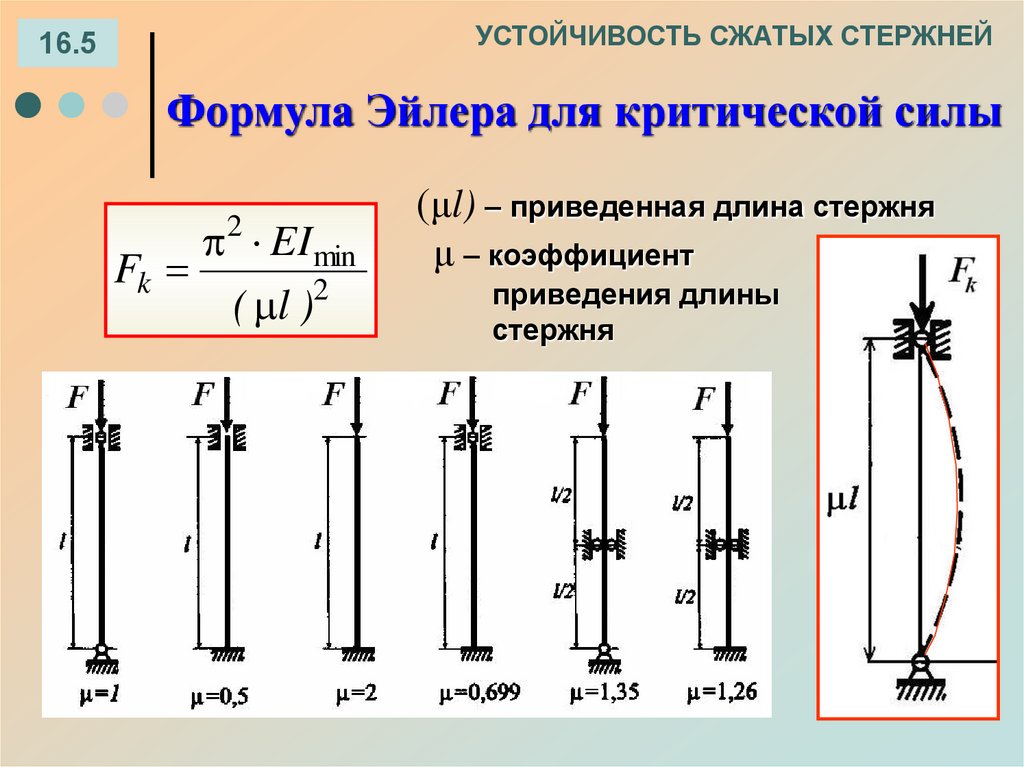
16.2. Формула Эйлера для критической силы
111. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
16.2УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
Понятие об устойчивости
первоначальной формы равновесия
При отклонении системы от положения равновесия
после устранения причин, вызывающих это отклонение,
различают три формы равновесия системы:
Устойчивое равновесие - система возвращается в первоначальное
положение.
Неустойчивое равновесие - система не возвращается в исходное
положение, а отклоняется от него еще больше.
Безразличное равновесие - новое положение системы после
отклонения от исходного остается равновесным и
после удаления внешнего воздействия.
112.
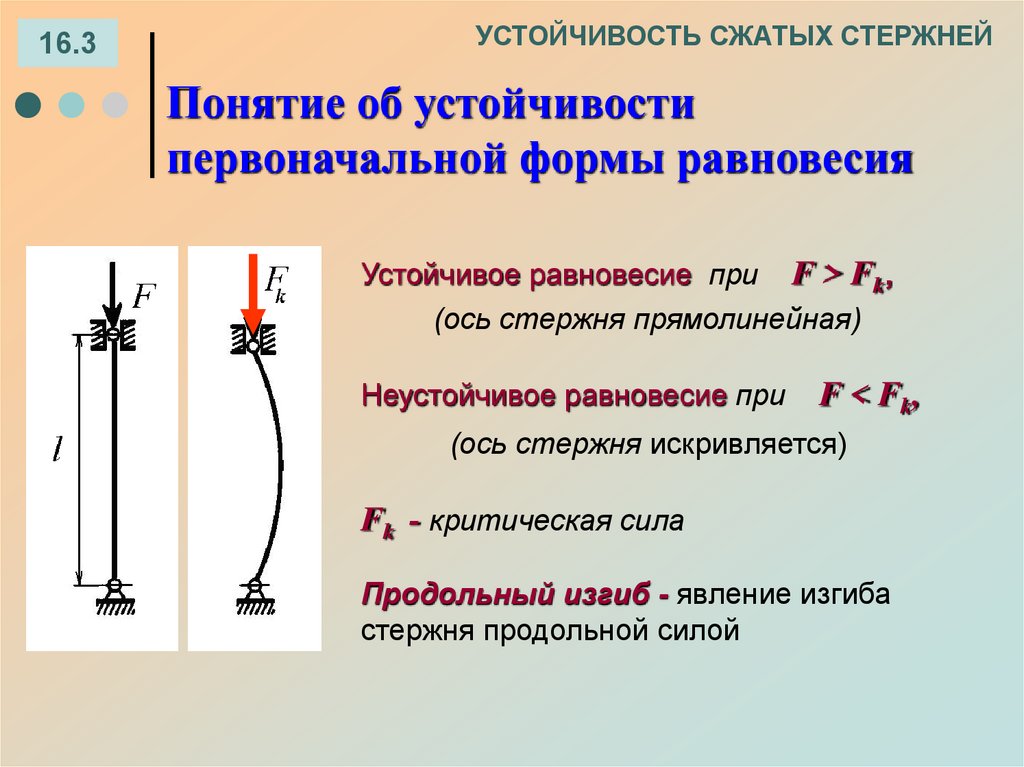
16.3УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
Понятие об устойчивости
первоначальной формы равновесия
Устойчивое равновесие при F > Fk,
(ось стержня прямолинейная)
Неустойчивое равновесие при
F < Fk,
(ось стержня искривляется)
Fk - критическая сила
Продольный изгиб - явление изгиба
стержня продольной силой
113.
16.4УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
Понятие об устойчивости
первоначальной формы равновесия
Для обеспечения устойчивости определяют
допускаемую нагрузку на сжатый стержень.
Fk
Fдоп
nу
Fk - критическая сила
nу - коэффициент запаса устойчивости
для стали пу = 2 … 4,
114.
16.5УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
Формула Эйлера для критической силы
М = -Fk y ;
ЕImin у"= ± М .
EIminy" = -Fk y.
Пусть Fk / (EImin) = α2,
у" + α2у = 0,
у = Asin αx + Bcos αx
В = 0, т.к.
при х = 0 прогиб у = 0.
y = A sin αx.
при х = l прогиб у = 0
Поэтому
у = A sin αl = 0
sin αl = 0, или αl = πn
Fk
EImin
n 2 2 EImin
Fk
l2
при n = 1 получаем
2 EImin
Fk
l2
115.
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ16.5
Формула Эйлера для критической силы
EImin
Fk
2
( l )
2
(μl) – приведенная длина стержня
μ – коэффициент
приведения длины
стержня
116. ЛЕКЦИЯ 17 План:
МЕХАНИКА17.1
Модуль 2.
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
УСТОЙЧИВОСТЬ
Устойчивость сжатых стержней
ЛЕКЦИЯ 17
План:
17.1. Пределы применимости формулы Эйлера.
17.2. Устойчивость сжатых стержней за пределами упругости
17.3. Расчет на устойчивость с помощью коэффициента снижения
допускаемого напряжения
117. УСТОЙЧИВОСТЬ
17.1УСТОЙЧИВОСТЬ
УСТОЙЧИВОСТЬ СЖАТЫХ
СТЕРЖНЕЙ
_________________________________________________________________
ЛЕКЦИЯ 8
_________________________________________________________________
План
17.1. Пределы применимости формулы Эйлера.
17.2. Устойчивость сжатых стержней за
пределами упругости
17.3. Расчет на устойчивость с помощью
коэффициента снижения допускаемого
напряжения
118. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
17.2ПРЕДЕЛЫ ПРИМЕНИМОСТИ
ФОРМУЛЫ ЭЙЛЕРА
Fk 2 EImin
k
пц
2
A
( l ) A
Imin /A, = i2min, тогда
k
l
imin
2
2 E imin
( l )
2
пц
- гибкость стержня
2 E
k 2 пц
Условие применимости
формулы Эйлера:
2 Е
пц
или
λ ≥ λ0
λ ≥ 100
для чугуна - λ ≥ 80,
для алюминиевого сплава - λ ≥ 60
для стали -
119.
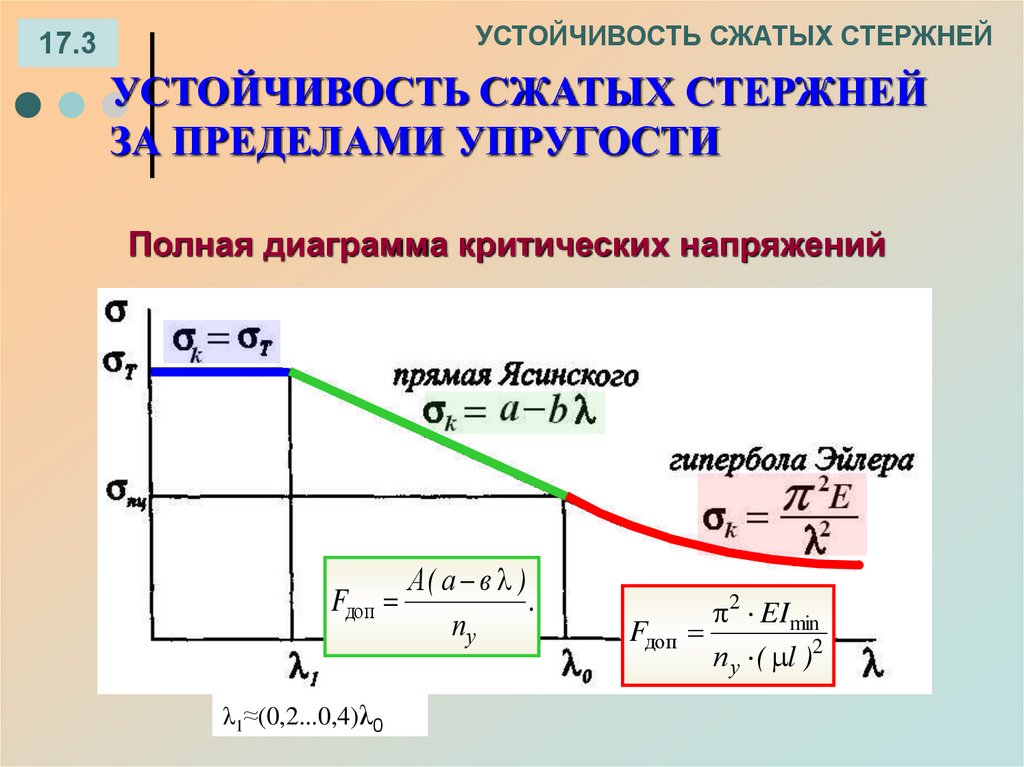
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ17.3
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
ЗА ПРЕДЕЛАМИ УПРУГОСТИ
Полная диаграмма критических напряжений
А( а в )
Fдоп
.
пу
λ1≈(0,2...0,4)λ0
2 EImin
Fдоп
п у ( l )2
120.
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ17.4
РАСЧЕТ НА УСТОЙЧИВОСТЬ
С ПОМОЩЬЮ КОЭФФИЦИЕНТА СНИЖЕНИЯ
ДОПУСКАЕМОГО НАПРЯЖЕНИЯ
F
с ,
A
где: [σс] - допускаемое напряжение сжатия;
φ - коэффициент снижения
допускаемого напряжения (коэффициент
продольного изгиба)
Допускаемое напряжение
при расчете на устойчивость:
у с .
Площадь сечения стержня:
F
A
.
с
Значение φ подбирается последовательно, начиная с 1 0 ,5






























































 Механика
Механика








