Геометрическое моделирование

1. Геометрическое моделирование

Аффинные преобразования на
плоскости

2. Общий вид аффинного преобразования

Аффинные преобразования
координат на плоскости.
(x, y) - двумерная система координат.
(X, Y) - координаты в новой системе координат.

3. Общий вид аффинного преобразования

X Ax By C
Y Dx Ey F
A, B, C, D, E, F - константы
Или в матричной форме:
X A B C x
Y D E F y
1 0 0 1 1

4. Обратное преобразование

x A X B Y C
y D X E Y F
Обратное преобразование также является
аффинным

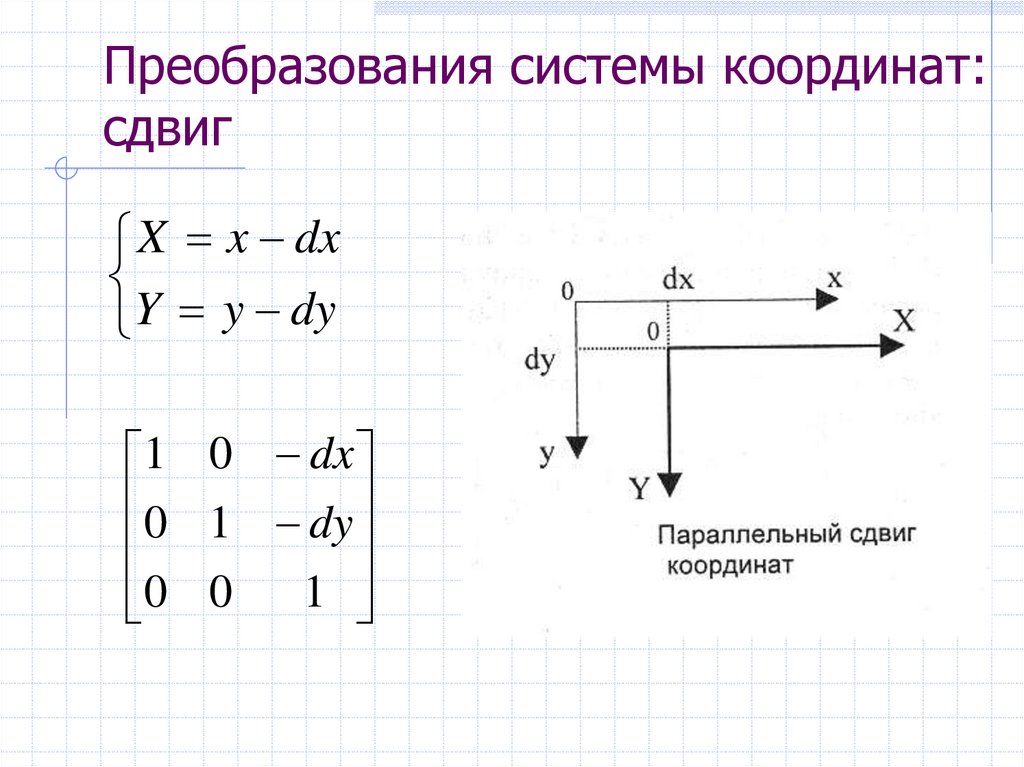
5. Преобразования системы координат: сдвиг

X x dx
Y y dy
1 0 dx
0 1 dy
1
0 0

6. Преобразования системы координат: сдвиг

обратное преобразование
x X dx
y Y dy
1 0 dx
0 1 dy
0 0 1

7. Преобразования системы координат: растяжение/сжатие

X x kx
Y
y
k
y
0
1 k x
0 1k
y
0
0
0
0
1

8. Преобразования системы координат: растяжение/сжатие

обратное преобразование
x Xk x
y
Yk
y
k x
0
0
0
ky
0
0
0
1

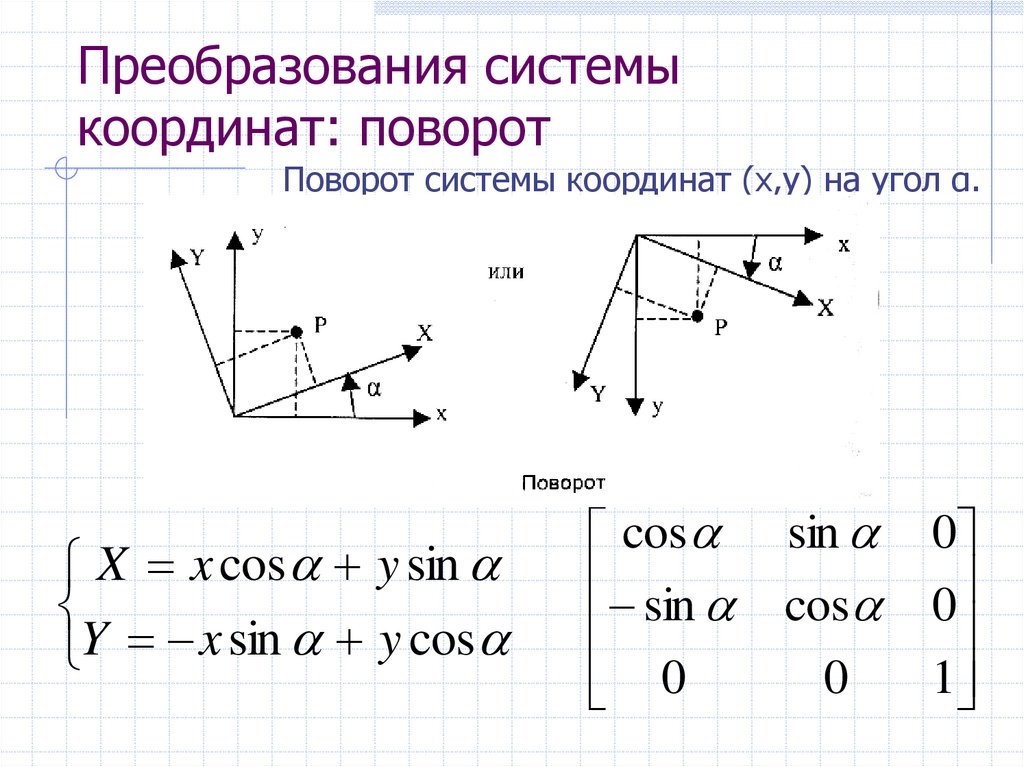
9. Преобразования системы координат: поворот

Поворот системы координат (x,y) на угол α.
X x cos y sin
Y x sin y cos
cos
sin
0
sin
cos
0
0
0
1

10. Преобразования системы координат: поворот

обратное преобразование
x X cos Y sin
y X sin Y cos
cos
sin
0
sin
cos
0
0
0
1

11. Аффинные преобразования объектов на плоскости

Система координат неподвижна.
Преобразованиям подвергаются все точки
объекта.
x, y - старые координаты точки
X, Y - новые координаты точки

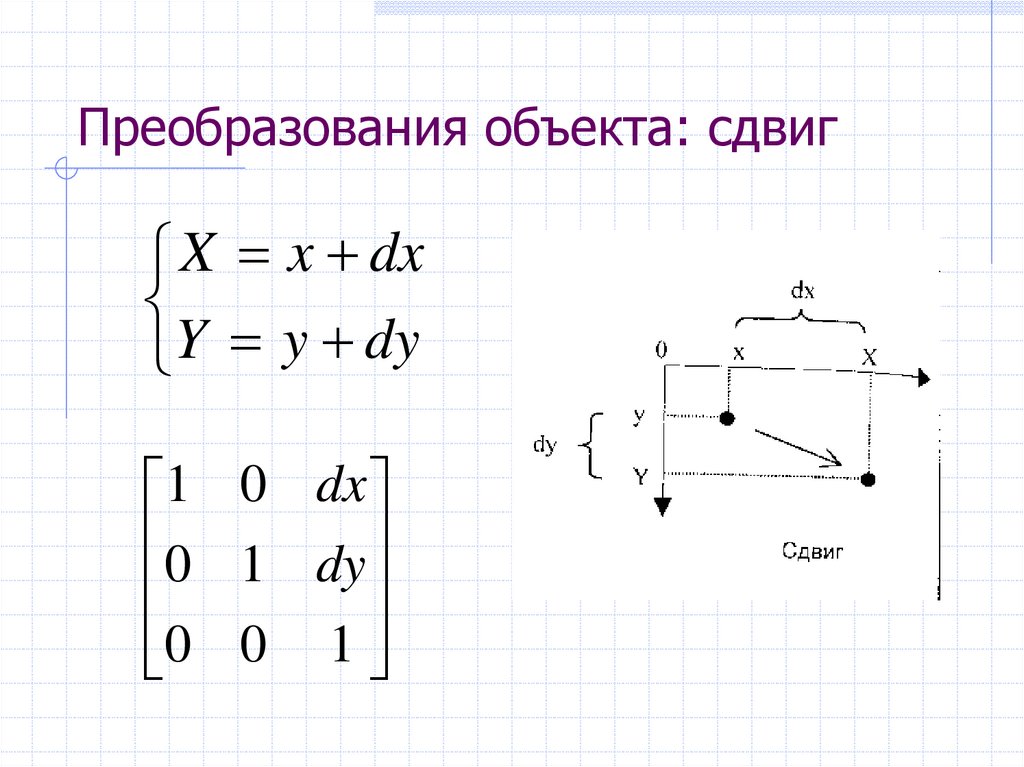
12. Преобразования объекта: сдвиг

X x dx
Y y dy
1 0 dx
0 1 dy
0 0 1

13. Преобразования объекта: сдвиг

обратное преобразование
x X dx
y Y dy
1 0 dx
0 1 dy
1
0 0

14. Преобразования объекта: растяжение/сжатие

X xkx
Y
yk
y
k x
0
0
0
ky
0
0
0
1

15. Преобразования объекта: растяжение/сжатие

обратное преобразование
x X kx
y
Y
k
y
0
1 k x
0 1k
y
0
0
0
0
1

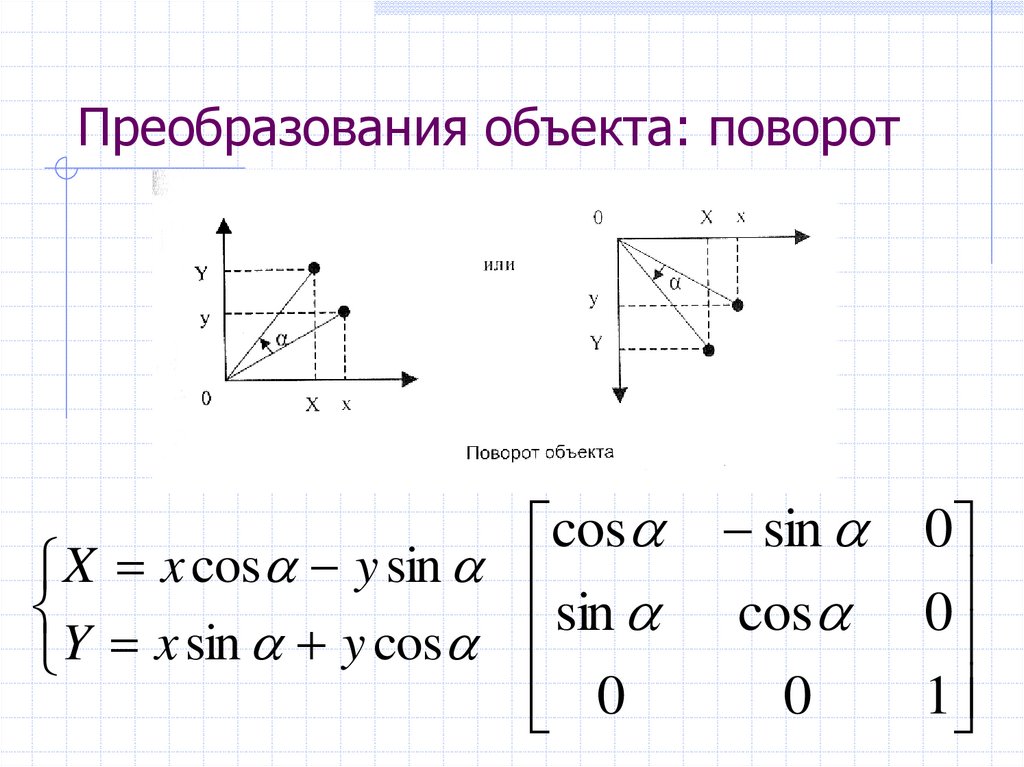
16. Преобразования объекта: поворот

cos
X x cos y sin
sin
Y x sin y cos
0
sin
cos
0
0
0
1

17. Преобразования объекта: поворот

обратное преобразование
x X cos Y sin
y X sin Y cos
cos
sin
0
sin
cos
0
0
0
1

18. Комбинация преобразований

Пусть требуется
повернуть точку
с координатами
(x,y) на угол α
относительно
точки (x0,y0)

19. Комбинация преобразований

В матричной форме одно из решений может быть
записано следующим образом: