Похожие презентации:
Моделирование случайных событий
1.
2. Моделирование случайных событий
01
,
p 1 p
ξ
p 1,
else 0
Попарно несовместны (A1, A2,…, An), P(Ai)=pi
ξ
1
p1
2
p2
n
. . . pn
. . .
3. Моделирование случайных событий
3. 2 независимых совместных события A и BP(A)=pA, P(B)=pB
1 ,
2 ,
A1=AB, A2=A B, A3= AB, A4= A B
1 2 3 4 p1=pApB, p2=pA(1-pB),
, p3=(1-pA)pB, p4=(1-pA)(1-pB)
p1 p2 p3 p4
4. Моделирование случайных событий
4.А и В – зависимые
совместные события
Р(А)=рА
Р(В)=рВ
Р(АВ)=рАВ
р
=р
р
=р
-р
1
АВ
2
А
АВ
3
1
2
4
,
р3=рВ-рАВ
p
p
p
p
1 2 3 4
р4=1-рА-рВ+рАВ
5. Моделирование непрерывных случайных величин
p(x) на (a,b)x
F x p u du
a
6. Моделирование непрерывных случайных величин
Теорема 2: Сл.в. , удовлетворяющая уравнениюF( )= ,
(2)
имеет плотность распределения p(x).
Доказательство: т.к. функция F(x) строго
возрастает в интервале (a,b) от F(a)=0 до F(b)=1, то
уравнение (2) имеет единственный корень при
каждом .
7. Доказательство теоремы 2
P x x dxP F x F x dx
И т.к. сл.в.
р.р. в интервале (0,1), то
8. Преобразования случайных величин
Пример: Экспоненциальная случайная величинаопределена на (0, ) с плотностью
p(x)=a*exp(-ax)
x
F x ae au du 1 e ax
0
1
ln 1
a
1
ln
a
9. Моделирование n-мерной случайной точки с независимыми координатами
Координаты n-мерной сл. т. QQ( 1 , , n )
FQ ( x1 , , xn ) F1 ( x1 ) F ( xn ),
Fi ( i ) i
10. Моделирование n-мерной случайной точки с независимыми координатами
Пример: Сл.т. Q в декартовых координатах( 1, 2) р.р. в прямоугольнике П
a
1
x b1 , a2 y b2
Плотность вероятностей т. Q постоянна в П:
1
, x, y
pQ ( x, y ) (b2 a2 )(b1 a1 )
0
11. Моделирование n-мерной случайной точки с независимыми координатами
Тогда1
pi bi ai ,
0
xi (ai , bi )
Следовательно, 1 и 2 равномерно распределены в
интервалах (a1,b1), (a2,b2). И эти координаты
независимы. Тогда
Fi ( i )
i ai
bi ai
i
12.
Замена переменныхQ( 1 , , n )
Q ( 1, , n )
вВ
в В’
(х1, х2,…,хn)
(y1, y2,…,yn)
( x1 , , xn )
pQ ( y1 , , yn ) pQ ( x1 , , xn )
.
( y1 , , yn )
13.
Преобразования вида g ( 1 , 2 )Пусть 1 и 2 два независимых случайных числа.
Могут существовать функции g(x,y) такие,
что случайная величина g( 1, 2)
имеет функцию распределения F(x)
14. Применение полярных координат
Q( , ) имеет плотностьpQ ( x , y ) c( r ),
r x y
2
2
:
R1 r R2
15. Применение полярных координат
yr
φ
x
x r cos ,
y r sin ,
16.
Применение полярных координатx
r
Якобиан = y
r
x
cos
y
sin
r sin
r
r cos
pQ (r , ) r c(r )
17. Применение полярных координат
R1 r R2 ,0 2 ,1
r c(r ) 2 r c(r )
p (r ) p ( ),
2
1
p (r ) 2 r c(r ); p ( )
;
2
2 r c(r )dr 1 ;
2
2
R1
pQ (r , ) r c(r )
18. Моделирование нормальной случайной величины
Пример: Смоделировать сл.в. ~N(0,1)1
p ( x)
e
2
~ N (0,1)
x2
2
, x ;
Q( , )
19.
1pQ ( x, y) p ( x) p ( y)
e
2
2
p (r ) r e
r
2
r2
2
,0 r
1
, p ( )
2
20.
Моделирование нормальной случайной величины2 1 , 2 ln 2 ,
2 ln 2 cos 2 1 ,
2 ln 2 sin 2 1
21. Моделирование нормальной случайной величины
a,2
0 ,
( a)
0 ,
a 0
22. Метод суперпозиции
nF ( x) Ck Fk ( x),
k 1
Ck>0
n
,
1 2 n
,
C1 C2 Cn
C
k 1
P( =k)=Ck
k
1
23. Метод суперпозиции
Теорема 3: Пусть 1 и 2 - независимые сл.числа. Еслипо числу 1 разыграть =k, затем из уравнения
Fk ( ) 2
определить , то ф.р. есть F(x).
Доказательство: По формуле полной вероятности вычислим ф.р. величины , построенной в теореме:
m
m
k 1
k 1
P( x) P x k P( k ) Fk ( x) Ck F ( x)
24. Метод суперпозиции
Пример: Случайная величина определена на0<x<1 и имеет функцию распределения
n
F ( x) Ck x k ,
k 1
Считаем, что
Тогда, если
где все Ck 0.
Fk ( x) x .
k
k 1
k
j 1
j 1
C j 1 C j ,
1
то
2 k.
25.
Преобразования видаg ( 1 , , n )
Извлечение корней из случайного числа
F(x)=xn при 0<x<1,
P(γ<x)=x
Fξ(x)=P(γ1<x, γ2<x,…,γn<x)=P(max(γ1, γ2,…,γn)<x)
max( 1 , , n )
26. Преобразования вида
g ( 1, , n )Моделирование Гамма-распределения
-1 n-1 -x
pn(x)= (n-1) x e , n 1;
(n)=-ln( 1 2… n)
27. Преобразования вида
g ( 1, , n )Моделирование биномиальных
распределений
k k
n-k
P( =k)=Cn p (1-p) ,
k=0,1,…,n
γ1<p
γ2<p,
…
γn <p
ξ=k
28. Приближенное моделирование нормального распределения
M =n/2, D =n/12,n
i ,
i 1
M
N 0,1 ,
D
P( x)
1
2
x
e
t2
2
dt.
n
n
3
2 i 1
n i 1
12
для n=12
i 6
i 1
29. Методы отбора
Q , если QЄBЭффективность= вероятность отбора,
или
P Q B
30. Методы отбора
Моделирование усеченных распределенийПусть
~ p( x) на (a,b):
b
p( x)dx 1.
a
И пусть p1(x) , усеч. р. на (a`,b`) (a,b)
p1 ( x)
p( x)
b`
p( x)
p( x)dx
a`
ξ=η, если η (a`,b`)
31. Методы отбора
Пример:~ e
x
на (0, )
(2, ), p1 ( x)
p ( x)
e
x
dx
2
Э e
2
x
dx e
t
2
e
2
32. Метод Неймана
Пусть на (a;b) с p(x) c:y
y=p(x)
c
`=a+(b-a) 1,
`=c 2
.
Q( `, `)
0
a
`
b
x
33. Метод Неймана
Теорема 4: Пусть 1 и 2 - независимые сл.числа,
a 1 (b a), c 2 .
Сл.в. , определенная
условием = , если ’<p( ),
имеет пл.в. p(x).
34. Метод Неймана
Доказательство: т.Q( )~р.р. в (a<x<b, 0<y<c)p(x`,y`)=1/c (b-a)
P z, p( )
P z P z / p( )
P p( )
35. Метод Неймана
Эффективность метода Нейманаэ=p( <p(x))=1/c(b-a)


















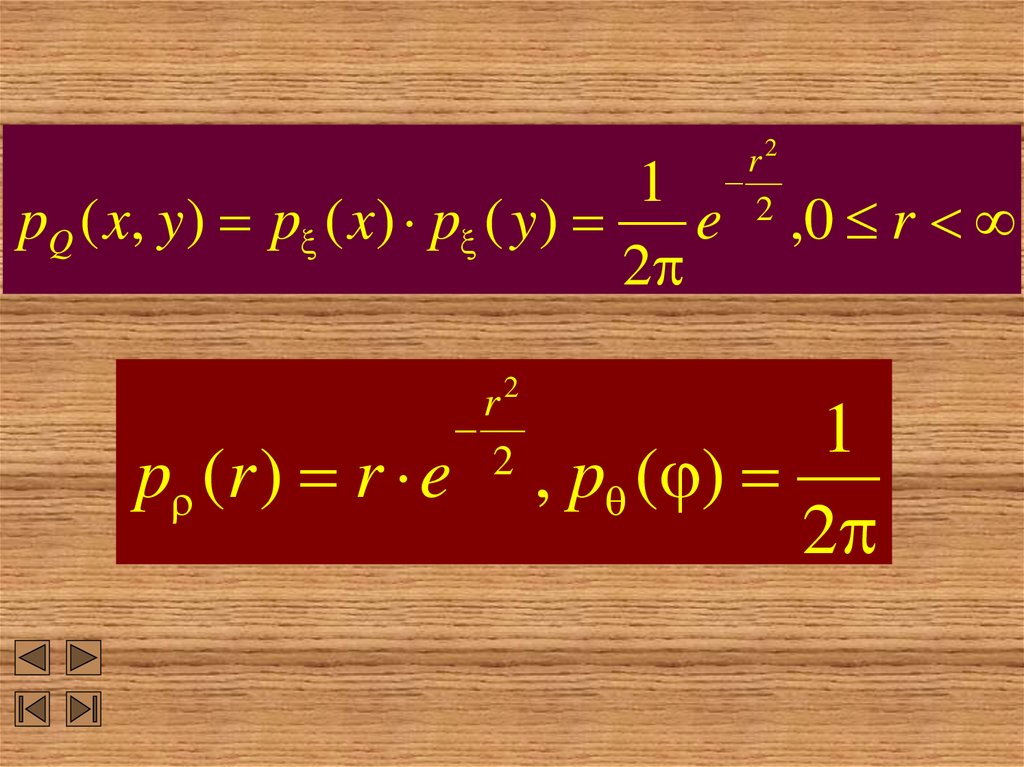
















 Математика
Математика








