Элементы химической термодинамики

1.

ЭЛЕМЕНТЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ
Первый закон термодинамики и химические процессы
Закон Гесса: тепловой эффект химической реакции зависит только от начального
и конечного состояния системы, но не зависит от пути перехода.
Закон Гесса является одним из частных случаев первого закона термодинамики.
Рассмотрим реакцию взаимодействия водорода и кислорода, проходящую в
цилиндре под невесомым поршнем, через который реагирующие газы
воспринимают давление окружающей среды; цилиндр размещен в термостате
окружающей среде с постоянной температурой.
В начальном состоянии в цилиндре имеется 1 кмоль Н2 (т. е. 2 кг Н2) и 0,5 кмоль
O2 (8 кг), смесь газов имеет стандартное давление 101,325 кПа и стандартную
температуру 298,15 К (25°С).
Возбудим реакцию с помощью электрической искры. Согласно уравнению
H 2 0,5O2 H 2O (г),
после завершения реакции образуется 1 кмоль Н2О в газообразной форме.
Измерения показывают, что количество выделившейся при горении водорода
теплоты в данном случае равно Qp = 242 000 кДж.

2.

Кроме того, изменился объем системы: в начальном состоянии было 1,5
кмоля, в конечном – 1 кмоль.
Поскольку р и Т постоянны (в процессе реакции температура газовой смеси
возросла, но затем снова вернулась к значению 298,15 К, что позволяет считать
Т=const), то по закону Авогадро объем системы уменьшается в 1,5 раза;
следовательно, окружающая среда совершает над системой работу сжатия:
L n иi n пi pV ,
где nиi – число киломолей исходных веществ; nпi – число киломолей продуктов
реакции; Vμ – объем 1 кмоля при стандартных р и Т.
В расчет принимаются только газообразные участники реакции. С учетом
уравнения Менделеева–Клапейрона выражение для работы против давления
окружающей среды принимает вид:
L n иi n пi R T .
(1)
В данном случае имеем (1,5 – 1)⋅ 8,314⋅ 298,15 = 1239 кДж.
Уравнение первого закона термодинамики со значениями входящих в него
величин можно представить следующим образом:
Q и п U и п Lи п ,
–242 000 кДж = –240 761 кДж – 1239 кДж.
(2)

3.

Уравнение (2) можно записать и в таком виде:
Q и п (U п U и ) p (V п V и ) (U п pV п ) (U и pV и ),
где V и V
n ; V V n .
иi
п
пi
С учетом определения энтальпии H = U + pV имеем:
Q и п Q p H ,
(3)
где Qp – тепловой эффект реакции (изобарный); для экзотермической реакции
Qp>0, для эндотермической Qр<0.
Уравнение (3) есть результат применения первого закона термодинамики к
химической реакции при р, T = const. Одновременно это уравнение выражает
закон Гесса; действительно, изменение энтальпии – параметра состояния –
определяется только ее значениями в начальном и конечном состояниях.
Например, тепловые эффекты реакций горения углерода в одну стадию (C →
CO2) и в две стадии (C→CO→CO2) равны между собой.

4.

Описанную выше реакцию взаимодействия водорода с кислородом можно
провести при постоянном объеме.
Измерения показывают, что если начальное состояние – стандартное, то при
прохождении реакции в условиях V, T = const выделяется теплота
Qv = 240 761 кДж.
Этот результат согласуется с первым законом термодинамики и с законом Гесса:
(4)
Q v U .
Изохорный тепловой эффект реакции Qv не зависит от пути перехода от исходных
веществ к продуктам реакции, поскольку величина ΔU определяется только
начальным и конечным состояниями. Работа изменения объема в данном случае
равна нулю.
Конечное состояние изохорно-изотермической реакции 2 (p1, V, T) в
рассмотренном случае отличается от конечного состояния 2 изобарноизотермической реакции (p, V1, T).
Однако U2 U1 = U2' U1, поскольку внутренняя энергия идеального газа зависит
только от температуры, а химический состав и масса системы в состояниях 2 и 2
одинаковы [18 кг Н2О (г)].

5.

Тогда из уравнений (2)–(4) и (1) получим:
Q p Q v n пi n иi R T .
(5)
Если число киломолей при прохождении реакции не изменяется, т. е.
n n 0,
пi
иi
то уравнение (5) принимает вид: Qp = Qv.
Практическое значение закона Гесса заключено в возможности рассчитывать
энтальпию реакции
H ni H i п ni H i и
(6)
по относительно небольшому объему справочных данных; величина ΔU,
необходимость определения которой возникает значительно реже, может быть
рассчитана по уравнениям (3)–(5).
Принцип накопления и использования термохимических справочных данных
основан на одном из следствий закона Гесса, которое может быть выражено
следующим образом:
H1 2 (H 2 H 0 ) (H1 H 0 ).
(7)
Согласно уравнению (7), разность энтальпий реакций, идущих от одинаковых
начальных состояний к двум различным конечным состояниям, равна энтальпии
перехода от одного конечного состояния к другому.

6.

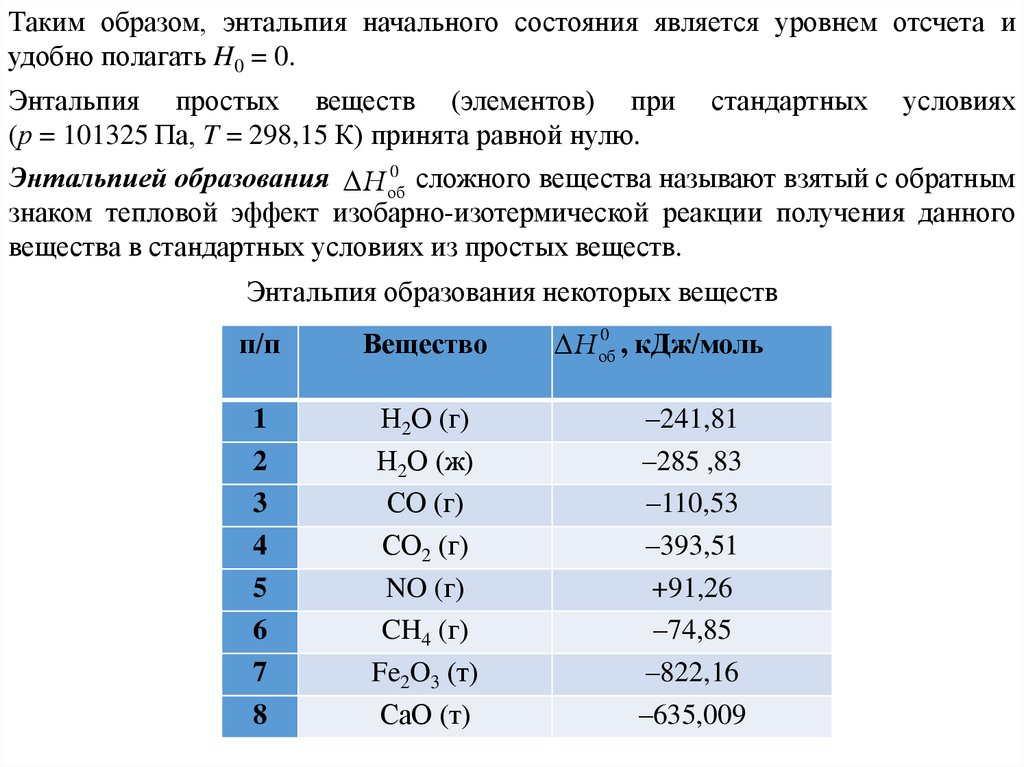
Таким образом, энтальпия начального состояния является уровнем отсчета и
удобно полагать H0 = 0.
Энтальпия простых веществ (элементов) при
(р = 101325 Па, T = 298,15 К) принята равной нулю.
стандартных
условиях
0
Энтальпией образования H об
сложного вещества называют взятый с обратным
знаком тепловой эффект изобарно-изотермической реакции получения данного
вещества в стандартных условиях из простых веществ.
Энтальпия образования некоторых веществ
п/п
Вещество
1
2
3
4
5
6
7
8
Н2О (г)
Н2О (ж)
СО (г)
СО2 (г)
NO (г)
CH4 (г)
Fe2O3 (т)
СаО (т)
0
, кДж/моль
H об
–241,81
–285 ,83
–110,53
–393,51
+91,26
–74,85
–822,16
–635,009

7.

При вычислении энтальпии произвольной реакции ΔH энтальпии образования
исходных веществ и продуктов можно считать обычными значениями энтальпии
Hi в том же смысле, в каком это понятие используется для воды и водяного пара
(там уровень отсчета взят 0°С).
Тогда уравнение (6) становится конкретной расчетной формулой
0
0
H ni H об
n
H
i обi .
i
п
и
(8)
В справочниках приводятся энтальпии образования нескольких тысяч
соединений, по этим данным можно рассчитать энтальпию десятков тысяч
различных реакций.
Используется и другое следствие закона Гесса: разность энтальпий реакций,
идущих от различных начальных состояний к одному конечному, равна
энтальпии перехода от одного начального состояния к другому.
Это следствие можно представить так:
H1 2 (H к H1 ) (H к H 2 ),
(9)
где Нк энтальпия конечного состояния.
Уравнение (9) позволяет использовать для расчета энтальпии произвольной
реакции энтальпии сгорания H сг0 веществ: энтальпии реакций взаимодействия
вещества с кислородом с образованием высших стабильных окислов (Н2О, СО2 и
т. п.).

8.

В этом случае энтальпия реакции равна
H ni H сг0 i ni H сг0 i .
п
и
(10)
Энтальпии сгорания могут быть определены с высокой точностью при сжигании
вещества в калориметрической бомбе. По энтальпиям сгорания рассчитывают
энтальпии образования органических веществ.
Указанные методы позволяют рассчитать энтальпию реакции при стандартной
температуре 25°С.
Для определения ΔН при любой температуре необходимо знать зависимость
ΔН = ΔН(Т).
Для реакции
n1A1 n 2 A2 n3 A3 n 4 A4
энтальпия равна
H (n3H 3 n 4 H 4 ) (n1H 1 n 2 H 2 ),
где Hi энтальпия 1 кмоля i-го вещества, кДж/кмоль.
(11)

9.

Продифференцируем обе части выражения (11) по Т при р = const:
H H 3
H 4 H 1
H 2
n3
n4
n1
n2
.
T p T p
T p T p
T p
Учитывая, что ( H/ T)p = cp, кДж/(кмоль К), получим
H
n3 c p 3 n 4 c p 4 n1 c p1 n 2 c p 2 ,
T p
или в сокращенной форме
H
c p .
T p
(12)
Уравнение (12) выражает закон Кирхгофа: (д Н/дТ)р равен разности
между молярными теплоемкостямпри постоянном давлении
температурный коэффициент энтальпии реакции и продуктов
реакции
и исходных
веществ.
Для получения
расчетной
формулы необходимо проинтегрировать
выражение (12).
В общем случае
c pi a0i a1iT a 2iT 2 ... .

10.

Эту зависимость можно подставить в уравнение (12) и сгруппировать
коэффициенты для одинаковых степеней T. Например, для коэффициента при T2
получим
a2 (n3a 23 n 4a 24 ) (n1a 21 n 2a 22 ) ni a 2i п ni a 2i и .
(13)
Используя принцип, выраженный уравнением (13), уравнение (12) можно
записать следующим образом:
H
2
a
dT
a
TdT
a
T
dT ... .
0
1
2
T p
(14)
Интегрируя уравнением (14), получим
a1T 2 a 2T 3
H a0T
... const .
2
3
(15)
Константу интегрирования можно найти, рассчитав ΔH298 для стандартной
температуры T = 298,15 К; для этой цели можно использовать и известное
значение ΔHT для любой температуры Т.

11.

Второй закон термодинамики в применении к химическим реакциям
Второй закон термодинамики позволяет выяснить направление химической
реакции и положение химического равновесия.
Как известно, химическое равновесие устанавливается в результате двусторонней
химической реакции
n1A1 n 2 A2 n3 A3 n 4 A4
и описывается законом действующих масс: скорость гомогенной реакции при
Т=const пропорциональна произведению концентраций (или парциальных
давлений) реагирующих веществ, возведенных в степень их стехиометрических
коэффициентов.
В состоянии равновесия скорости прямой и обратной реакций равны:
kи p1n1 p2n2 kп p3n3 p4n4 ,
где pi – парциальные давления; kи и kп – скорости прямой и обратной реакций,
отнесенные к единичным парциальным давлениям.
Количественная оценка положения равновесия для химической реакции при
определенной температуре дается константой равновесия КР, равной
p3n3 p4n4
К Р n1 n2 .
p1 p2
(16)

12.

Основная практическая ценность выражения (16) состоит в возможности
рассчитать выход продуктов реакции при равновесии, если известны количества
исходных веществ, давление и значение КР.
Пусть, например, для реакции 0,5А1 + 2А2 = А3, осуществляемой под давлением р,
количества исходных веществ равны: 2 кмоль реагента А1 и 1 кмоль реагента А2.
Требуется определить количество х продукта А3 в состоянии равновесия; и
определенной температуре, если известно взятое из справочника значение КР при
этой температуре.
Для решения таких задач необходимо составить уравнение вида KP = f(x, р) на
основе формулы (16) и решить его относительно х; во многих случаях для
решения такого уравнения приходится использовать численные или графические
методы, так как уравнение оказывается высокой степени.
Парциальное давление компонента газовой смеси определяется выражением:
ni
pi pi ,
n
где n – полное количество киломолей.
В состоянии равновесия n3 = х и в соответствии с уравнением реакции
n1 2 0,5x ;
n 2 1 2x.

13.

Величина
n ni (2 0,5x ) (1 2x ) x 3 1,5x.
Определив парциальные давления pi и подставив их и в выражение (16), получим
x (3 1,5x )1,5
КР
.
0,5
2 1,5
(2 0,5x ) (1 2x ) p
(17)
Решив это уравнение, найдем объемную долю продукта A3 в равновесной смеси; в
процентах она составляет 100х/(3 – 1,5х).
Отметим, что величина КР, согласно выражению (16), зависит от соотношения
парциальных давлений, но не зависит от полного давления р; если изменить
объем реагирующей или равновесной газовой смеси, не изменяя ее температуру и
состав, то давление р изменится, но это никак не отразится на значении КР.
С другой стороны, в правую часть уравнения (17) входит p–1,5, при этом для
рассматриваемой реакции
n ni п ni и n3 (n1 n 2 ) 1,5.
Для идеально-газовой смеси в уравнение типа (17) всегда входит множитель pΔn,
т. е. KP = f(x) pΔn.
Таким образом, при изменении р величина f(x) должна измениться так, чтобы
сохранилось значение КР.

14.

Изменение f(x), а следовательно, и выхода продукта реакции х происходит в
соответствии с принципом Ле Шателье-Брауна: при воздействии на равновесную
систему в ней развиваются процессы, стремящиеся как бы ослабить результат
этого воздействия.
Рассматриваемая реакция идет с уменьшением объема (Δn < 0), поэтому при
увеличении р происходит некоторое увеличение выхода продукта х, объем
системы при этом уменьшается, вследствие чего результат повышения давления
ослабляется.
Принцип Ле Шателье-Брауна часто применяется для качественного анализа
равновесия химических реакций и фазовых переходов, других равновесных
состояний при разнообразных воздействиях – механических, тепловых и др.
Рассмотренные здесь положения, касающиеся вопроса о химическом равновесии,
не имеют никакой видимой связи со вторым законом термодинамики.
Между тем общие принципы термодинамического равновесия, о которых уже
говорилось, применимы, конечно, и к химическим реакциям.
Условие максимума энтропии, справедливое для изолированной (или даже
закрытой адиабатной) системы, применяется не только для простых (т. е.
гомогенных однокомпонентных) систем, его можно использовать и для анализа
систем с фазовыми и химическими превращениями.

15.

Наиболее последовательный и простой путь такого использования связан с
методом термодинамических потенциалов Гиббса.
Понятие термодинамического потенциала поясним на примере изменения
внутренней энергии. Для простой системы с произвольной массой m
объединенное выражение первого и второго законов термодинамики можно
записать так:
dU TdS pdV .
(18)
Для адиабатной системы dS = 0 и из выражения (18) получаем:
pdV dU .
(19)
Если процесс обратим, то pdV = dL = –dU, т. е. работа равна изменению
внутренней энергии, взятому с обратным знаком.
По аналогии с механикой внутреннюю энергию называют термодинамическим
потенциалом.
Если процесс необратим, то, согласно выражению (19), dLн < dL. Таким образом,
величина –dU равна максимальной работе, реальная работа всегда меньше.
Термодинамический потенциал U может быть использован в качестве критерия
термодинамического равновесия.

16.

По условию система является закрытой (m = const). Прекратив подвод к системе
энергии в виде теплоты (dS = 0) и в виде работы (dV = 0), получим
изолированную систему. Для нее из выражения (18) имеем
(20)
dU 0.
Следовательно, в изолированной системе по второму закону термодинамики
могут происходить необратимые процессы с уменьшающейся внутренней
энергией (dUн < 0) или в идеализированном варианте обратимые процессы с
постоянной внутренней энергией (dU = 0).
Реально в изолированной системе внутренняя энергия будет уменьшаться до
минимума и затем сохранять постоянное значение. Достаточные условия
минимума функции U = U(S, V) имеют вид:
dU 0; d 2U 0.
(21)
Здесь также проявляется аналогия с механической системой: известно, что
условие равновесия в поле сил тяжести в простейшем случае состоит в наиболее
низком расположении центра тяжести; при этом потенциальная энергия системы
имеет минимальное значение.
Понятие потенциала связано с работой, поэтому имеет смысл рассмотреть
процесс совершения работы не только без подвода теплоты, как это сделано
выше, но и с подводом теплоты dQ = TdS от теплоотдатчика с температурой Т.

17.

Тождественные
преобразования
выражения
(18)
позволяют
найти
термодинамический потенциал и для этого случая. Прибавим и вычтем в правой
части выражения (18) величину SdT и перенесем d(TS) в левую, тогда получим
dF SdT pdV ,
(22)
где F = U – TS – энергия Гельмгольца, или изохорно-изотермический потенциал
(кратко – изохорный потенциал).
Из выражения (22) следует, что при dT = 0 работа pdV = dL – dF, т. е. величина F
обладает свойствами потенциала для изотермического процесса.
Таким образом, изохорный потенциал F позволяет определить максимальную
работу при T = const и принимает минимальное значение при равновесии системы
в условиях T = const, V = const.
Наряду с работой изменения объема dL = pdV важное значение имеет полезная
работа dLп =Vdp. Термодинамическими потенциалами для полезной работы
являются уже упомянутая ранее энтальпия H(S, p) и изобарный потенциал
(энергия Гиббса) G(T, p), для которых объединенное выражение первого и
второго законов термодинамики имеет вид:
dH TdS Vdp ;
(23)
dG SdT Vdp.
(24)

18.

Термодинамические потенциалы U, F, H и G, а также энтропию S называют
характеристическими функциями (функциями состояния).
Каждая их этих функций связана с определенными термодинамическими
параметрами ее «естественными» переменными: U = U(S, V); F = F(T, V);
H=H(S, p); G = G(T, p); S = S(U, V).
С помощью любой характеристической функции и ее производных могут быть
выражены все термодинамические свойства системы.
Пусть, например, задана функция U = U(S, V). Сравнивая выражение полного
дифференциала dU = ( U/ S)VdS + ( U/ V)SdV с уравнением dU = TdS pdV,
получим p = ( U/ V)S + p(S, V).
Исключив из двух последних уравнений энтропию
термодинамическое уравнение состояния F(p, V, T) = 0.
S,
получим
Поскольку ( 2U/ S2)V = ( T/ S)V, то имеем
CV
U S V
U S
2
2
CV (S ,V ).
V
Зная изохорную теплоемкость CV и используя уравнение состояния, можно найти
изобарную теплоемкость Cp. Легко найти и остальные параметры: H, F, G и
другие.

19.

Таким образом, для произвольного состояния, определяемого значениями S и V по
выражению U = U(S, V), могут быть рассчитаны все остальные
термодинамические параметры.
Конкретный вид той или иной характеристической функции для определенной
системы методами термодинамики определить, конечно, нельзя.
Нахождение характеристических функций возможно, например, экспериментальным путем.
Расширим понятие термодинамического потенциала, вводя в рассмотрение более
сложные системы, такие как, например, системы с химическими или фазовыми
превращениями, а также открытые системы.
Внутренняя энергия двухфазной системы, состоящей из воды и водяного пара,
зависит от того, какая часть массы системы приходится на жидкую фазу и какая
на паровую.
Каждая фаза представляет собой открытую систему, внутренняя энергия которой
зависит от массы.
Внутренняя энергия смеси газов зависит от состава этой смеси.
Термодинамические потенциалы F, H и G связаны с внутренней энергией,
поэтому все сказанное справедливо и для них.

20.

Действительно, F = U TS, при этом F называют также свободной энергией, а TS
связанной энергией, их сумма равна внутренней энергии U;
энтальпия H = U + pV;
изобарный потенциал G = U + pV TS = H TS.
В последующем будем рассматривать только изобарный потенциал, так как
условия p = const, T = const являются наиболее распространенными.
В соответствии со сказанным изобарный потенциал многокомпонентной системы
зависит не только от давления и температуры, но и от количества отдельных
компонентов:
G G ( p ,T , n1 , n 2 ,..., nm ),
(25)
где ni количество киломолей i-го компонента, i =1, 2, …, m.
Дифференциал изобарного потенциала равен
m
dG ( G T ) p ,n dT ( G p )T ,n dp ( G ni ) p ,T ,n dni
i 1
или с учетом выражения (24) имеем
m
dG SdT Vdp i dni ,
i 1
где i химический потенциал i-го компонента, кДж/кмоль.
(26)

21.

Выражение (26) есть объединенное выражение первого и второго закона
термодинамики для многокомпонентной системы переменного состава.
Такое выражение можно получить и для трех других термодинамических
потенциалов, основываясь на формулах (18), (22) и (23).
Применительно к обратимым процессам выражения типа (26) становятся
уравнениями, их называют основными термодинамическими уравнениями
Гиббса.
Изменение количества компонента dni может происходить как из-за процессов
внутри системы (химические превращения, фазовые переходы), так и в связи с
поступлением компонента i через границу системы.
Для химических превращений удобнее измерять i в кДж/кмоль, для фазовых
превращений в однокомпонентной системе в кДж/кг; оба способа правильны.

22.

Составим три остальных выражения по типу выражения (26) для наиболее
простого случая открытой однокомпонентной системы с обратимыми
процессами; вместе с формулой (26) получим:
dU TdS pdV ( U n )S ,V dn ;
dF SdT pdV ( F n )T ,V dn ;
dH TdS Vdp ( H n )S , p dn ;
dG SdT Vdp ( G n )T , p dn.
(27)
Сравнивая уравнения (27) с выражением (26), видим, что частные производные в
правой части уравнений (27) есть выражение химического потенциала через
различные независимые переменные. Это подтверждается равенством всех
производных между собой:
( U n )S ,V ( F n )T ,V ( H n )S , p ( G n )T , p ,
(28)
которое легко доказать, если перенести два первых члена правой части любого из
уравнений (27) в левую часть.

23.

Зависимость (28) распространяется и на многокомпонентную систему. Она
раскрывает смысл химического потенциала: он равен изменению
термодинамического потенциала системы при изменении ni на 1 кмоль в
условиях
постоянства
естественных
переменных
данного
термодинамического потенциала и количеств nj, j i всех остальных
компонентов.
Произведение idni можно трактовать так же, как работу немеханического
характера: ведь
именно
вследствие
совершения
работы меняется
термодинамический потенциал системы.
Величина idni применительно к химическим превращениям называется
химической работой.
Условие равновесия термодинамической системы определяется выражением (24)
и имеет вид
(29)
dG 0.
Выражение (29) означает, что в состоянии равновесия изобарный потенциал
принимает минимальное значение, то есть dG = 0, d2G > 0.

24.

Для открытой многокомпонентной системы (или многокомпонентной системы
переменного состава, но замкнутой) в состоянии равновесия при p, T = const
имеем
dG i dni 0.
(30)
Установим связь термодинамического условия (30) для равновесного состояния с
условием (16) химического равновесия.
Убеждение в том, что такая связь существует, основано на том, что два способа
закон действующих масс и второй закон термодинамики используются для
количественной характеристики одного и того же факта равновесия системы.
Для химической реакции n1A1 + n2A2 = n3A3 + n4A4 определяют не элементарное
изменение dG, а конечное приращение изобарного потенциала G = Gп Gи
аналогично тому, как это делалось для энтальпии реакции H по формуле (6).
По уравнению (30) имеем:
dG ni i п ni i и .
(31)
Для расчетов по формуле (31) необходимо уметь определять величину i для
каждого компонента. Достаточно просто это можно сделать лишь для
реагирующей смеси идеальных газов.

25.

Определим вначале химический потенциал для 1 кг отдельно взятого идеального
газа.
Если dG SdT VdT , то
d sdT vdT .
Для T = const имеем
dp
d vdT RT
p
или после интегрирования
RT ln p const RT ln p f (T ).
Для определенного (стандартного) давления p = p0 имеем
0 (T ) RT ln p 0 f (T ).
Тогда, вычитая это уравнение из предыдущего, получим
0 RT (ln p ln p 0 ).
Если выбрать p0 = 1 МПа и выражать p также в МПа, то
0 (T ) RT ln p.

26.

Для реагирующей газовой системы вместо p следует брать парциальное давление
компонента pi, а так как i измеряется в кДж/кмоль, а не в кДж/кг, то вместо
газовой постоянной R, кДж/(кг·К), следует брать универсальную газовую
постоянную R , кДж/(кмоль·К).
С учетом сказанного получаем следующую формулу для химического потенциала
компонента реагирующей смеси идеальных газов:
i i0 (T ) R T ln pi .
(32)
Подсчитаем G по формуле (31):
G n 4 04 (T ) n 4R T ln p4 n3 30 (T ) n3R T ln p3
n1 10 (T ) n1R T ln p1 n 2 02 (T ) n 2R T ln p2 .
Сгруппировав подобные члены, получим более компактную запись последнего
выражения:
p3n3 p4n4
G (T ) R T ln n1 n2 ,
(33)
p1 p2
где pi парциальное давление i-го компонента для системы, которая еще не
0
достигла состояния равновесия; (T) сумма членов вида n1 1 (T ) .

27.

В состоянии равновесия G = 0, а парциальные давления pi принимают значения
равновесных парциальных давлений pi, по которым определяется константа
равновесия Кр в формуле (16). Принимая эти условия к выражению (33), имеем:
p3n3 p4n4
(T ) R T ln n1 n2 R T К р .
p1 p2
(34)
Подставляя (T) из уравнения (34) в уравнение (33), получаем:
p3n3 p4n4
G R T ln n1 n2 ln К р .
p1 p2
(35)
Уравнение (35) называется уравнением изотермы химической реакции, оно
получено Вант-Гоффом. Это уравнение устанавливает связь между
термодинамическим критерием равновесия и константой закона действующих
масс Кр.

28.

Если давления pi pi , т.е. принимают равновесные значения, то G = 0 и реакция
не идет.
Если первое слагаемое в квадратных скобках выражения (35) больше второго, то
G > 0. Это означает, что при осуществлении прямой реакции (слева направо)
изобарный потенциал возрастал бы, что запрещается вторым законом
термодинамики (29), следовательно, прямая реакция не идет, но зато может идти
обратная реакция (справа налево).
И, наконец, если первое слагаемое меньше второго, то G < 0 и идет прямая
реакция.
Значимость величины G для химической реакции не исчерпывается только ее
знаком, оказывается, важно и абсолютное значение величины G изменения
изобарного потенциала в реакции. Чем больше значение G , тем с большей
интенсивностью система стремится к состоянию равновесия.
Применительно к химическим реакциям величина G характеризует так
называемое химическое сродство: тенденцию исходных веществ вступать в
реакцию. Чем больше G при G < 0, тем больше термодинамическая
возможность протекания прямой реакции, тем большим химическим сродством
обладают реагенты.

29.

Величина G равна максимально возможной полезной работе, которую
совершает система при обратимом переходе в состояние равновесия в
изотермических условиях:
G Lп , при этом Lп LHп .
Если постоянно и давление, то dp = 0 и
Lп Vdp i ni dLп.хим ,
т.е. система совершает только полезную химическую работу. При этом говорят,
что максимальная работа химической реакции есть мера химического сродства.
Для практики важно предсказывать химическое сродство определенной реакции.
Например, необходимо установить для какой из двух реакций I или II
химическое сродство больше. С этой целью сравнивают величины GI и GII.
Сравнение нужно производить в сопоставимых условиях, т.е. при вычислении G
по формуле (35) должны быть TI = TII, К I К II .
Для температуры принимают стандартное значение 298,15 К, а при определении К
все давления pi берут единичными; при К 1 и ln К 0. Следует понимать, что
единицы измерения у величин pi и pi должны быть одинаковыми.

30.

В справочной литературе по расчетам химических равновесий давления pi
традиционно измеряются в атмосферах (1 атм = 101325 Па), поэтому единичные
0
давления равны pi 1 атм (для записанной ранее типовой реакции с четырьмя
веществами Ai общее давление равно 4 атм).
Для принятых условий (T = 298,15 К, pi0 101325 Па) стандартное изменение
0
изобарного потенциала реакции G298
, кДж/кмоль, согласно формулы (35) равно:
0
G298
8,314 298,15 ln К р .
(36)
Сравним, например, реакции окисления меди и золота:
Cu(т) + 0,5O2 = CuO(т);
2Au(т) + 1,5O2 = Au2O3(т);
0
G298
127,2 МДж/кмоль CuO;
0
G298
78,3 МДж/кмоль Au 2O3 .
Видно, что если поместить медь в атмосферу кислорода при давлении 1 атм и
0
температуре 298,15 К, то реакция окисления пойдет, так как G298
0;
0
для золота G298
0 и оно в стандартных условиях не окисляется.
Стандартное изменение изобарного потенциала
температуры, согласно уравнению (35), равно
G 0 R T ln К р .
G 0
.
Из уравнения (37) получаем К р exp
R T
G
для
произвольной
(37)
(38)

31.

Знание константы Кр позволяет решить основную практическую задачу: найти
выход продуктов реакции для заданных значений температуры и давления; такие
расчеты позволяют выбрать оптимальные условия проведения реакции.
Зная величину G0 при различных температурах, можно выбрать температуру,
для которой G0 < 0. Формулы (37) и (38) позволяют легко найти любую из
указанных величин, если известна вторая.
Экспериментальное определение константы Кр сложно и трудоемко. Прямое
измерение
равновесных
концентраций
при
высоких
температурах
затруднительно, поэтому применяют «закаливание» реагирующей газовой смеси
ее резкое охлаждение, что приводит практически к прекращению реакции и
сохранению равновесного состава, который подвергается анализу.
При проведении подобных экспериментов используется сложная герметичная
аппаратура с автоматическим поддержанием постоянной температуры.
Для некоторых реакций, которые можно осуществить в гальваническом элементе,
Кр определяется по измерению ЭДС элемента.
Все перечисленные выше сложности привели к необходимости решить проблему
путем нахождения G0 с последующим расчетом Кр по формуле (38).
Расчет G0 по справочным данным, полученным в результате относительно
простых калориметрических экспериментов, оказался возможным благодаря
третьему закону термодинамики.

32.

Для определения функции
дифференциальное уравнение.
G0
=
G0(T)
необходимо
составить
Поскольку G = H TS, то при T = const имеем G = H T S.
Сравнивая полный дифференциал dG(T, p) с уравнением (24), получаем
G
G
S
, или S
.
T p
T p
Тогда
G
G H T
.
T p
(39)
Это уравнение называется уравнением Гиббса-Гельмгольца.
Учитывая отдельно условие p = const, уравнение (39) можно записать в виде
GdT Td G HdT .
Разделив обе части уравнения на T 2, получим слева дифференциал частного
G/T:
H
G
d
2 dT .
T
T
(40)

33.

Подставив в левую часть величину G0/T из уравнения (37)
d ln К р
dT
H
.
2
R T
(41)
Уравнение (41) называют уравнением изобары реакции. Оно связывает
константу Кр с энтальпией реакции H и температурой.
Выражение функции H = H(T) дается уравнением (15), полученным из закона
Кирхгофа (12), поэтому уравнение изобары можно интегрировать:
H (T )
ln К р R
dT I .
2
T
1
(42)
Интеграл (42) берется просто, поскольку H(T) является многочленом, однако
постоянная интегрирования I может быть найдена только по известному
значению Кр для определенной температуры, т.е. вопрос сводится к измерению
Кр, что, как отмечено выше, нежелательно.
Интегрирование уравнения (40) или подстановка в уравнение (42) значения lnКр
из формулы (37) дает следующее выражение:
H (T )
G T
dT TI ,
2
T
0
в котором также имеется неопределенная постоянная интегрирования.
(43)

34.

Поскольку I в уравнении (43) может быть определена на основе третьего закона
термодинамики, однако вначале рассмотрим некоторые следствия из первых двух
законов.
Поскольку G H T S ,
то lim( G H ) limT S 0,
T 0
T 0
так как lim S , в силу того, что энтропия S имеет конечное значение.
T 0
Следовательно, при T 0 имеем G = H. По уравнению (39)
( G H )
d G
lim
lim
,
T 0
T
0
T
dT
однако предел левой части, согласно правилу Лопиталя, равен
d G d H
d G
lim
C p .
Tlim
T 0
0
dT
dT
dT
Отсюда Cp = 0 и, согласно закону Кирхгофа,
d H
0.
dT

35.

Таким образом, для реакции, проходящей в условиях T = const, p = const, вблизи
абсолютного нуля кривая H = H(T) пересекает ось ординат в точке H = G и
имеет горизонтальную касательную.

36.

Экспериментальные исследования поведения величин G и H при низких
температурах показали, что и кривая G = G(T) имеет при T 0
горизонтальную касательную, т.е.
d G
0.
dT
Это утверждение составляет основное содержание тепловой теоремы Нернста,
которая справедлива для конденсированных сред и исторически представляет
собой первую формулировку третьего закона термодинамики.
Из условия d G/dT = 0 следует, что S = S2 S1 = 0.
В связи с этим третий закон формулируется так: при T 0 энтропия
равновесной системы принимает одну и ту же для всех систем постоянную
величину, которую можно положить равной нулю.
Эквивалентной формулировкой является утверждение о недостижимости
абсолютного нуля, основанное на том, что при T 0 изотермический и
адиабатный процессы совпадают, поэтому невозможно как адиабатическое
понижение температуры, так и изотермический отвод теплоты.

37.

Важным практическим следствием третьего закона является возможность
рассчитывать химические равновесия по калориметрическим данным.
Из уравнения (14) следует, что a0 = 0, так как при T 0 имеем d H/dT = 0.
С учетом этого подстановка H(T) в уравнение (43) после несложных
преобразований дает:
a1T 2 a 2T 3
G
H T 0 TI ;
2
6
d G 0
a 2T 2
2
a1T
I.
dT
2
0
(44)
(45)
Поскольку при T 0 имеем d G0/dT = 0, то по (45) I = 0.
Это дает возможность вычислять G0 по уравнению (44), если известны
коэффициенты a1, a2 температурной зависимости теплоемкости и энтальпии
реакции H при T 0.
Однако чаще всего для расчета G0 используют формулу G0 = H0 T S0, куда
входят стандартные термодинамические величины: энтальпия реакции,
определяемая законом Кирхгофа, и изменение энтропии в реакции, определяемое
формулой
S 0 ni Si0 ni Si0 ,
п
и
где