Параллельность прямых, прямой и плоскости

1. Параллельность прямых, прямой и плоскости

1

2.

2

3.

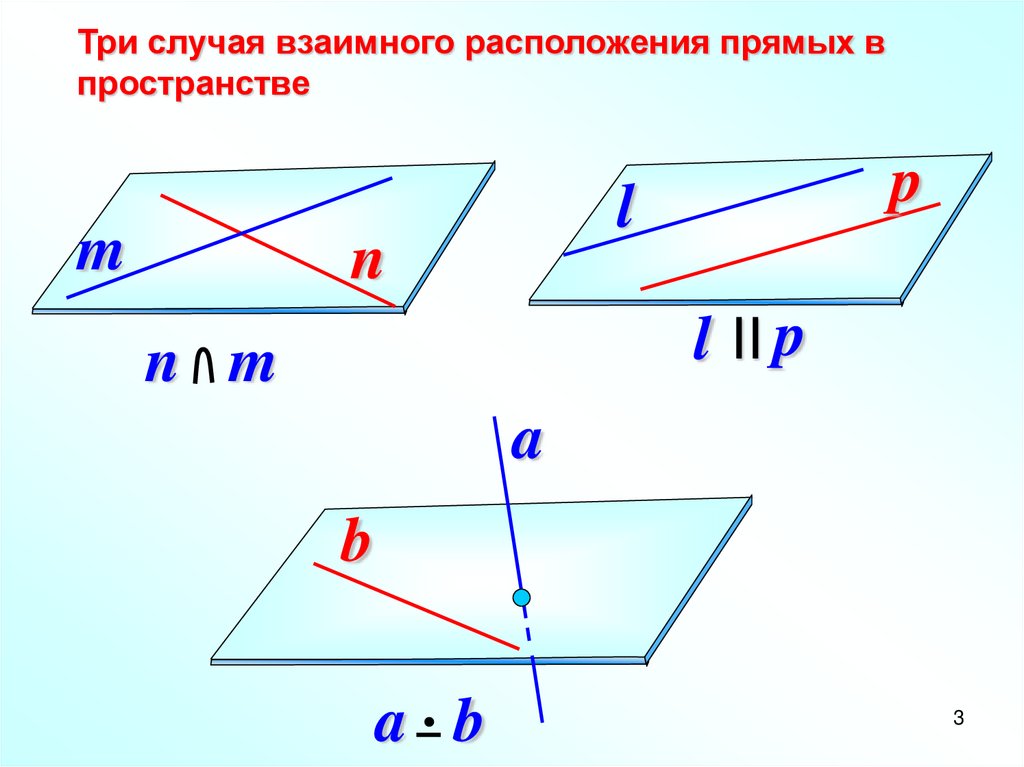
Три случая взаимного расположения прямых в
пространстве
m
p
l
n
l II p
n m
a
b
a b
3

4.

Планиметрия
Стереометрия
Две прямые на
плоскости называются
параллельными, если
они не пересекаются.
Две прямые в
пространстве
называются
параллельными, если
они лежат в одной
плоскости и не
пересекаются.
aIIb
aIIb
4

5.

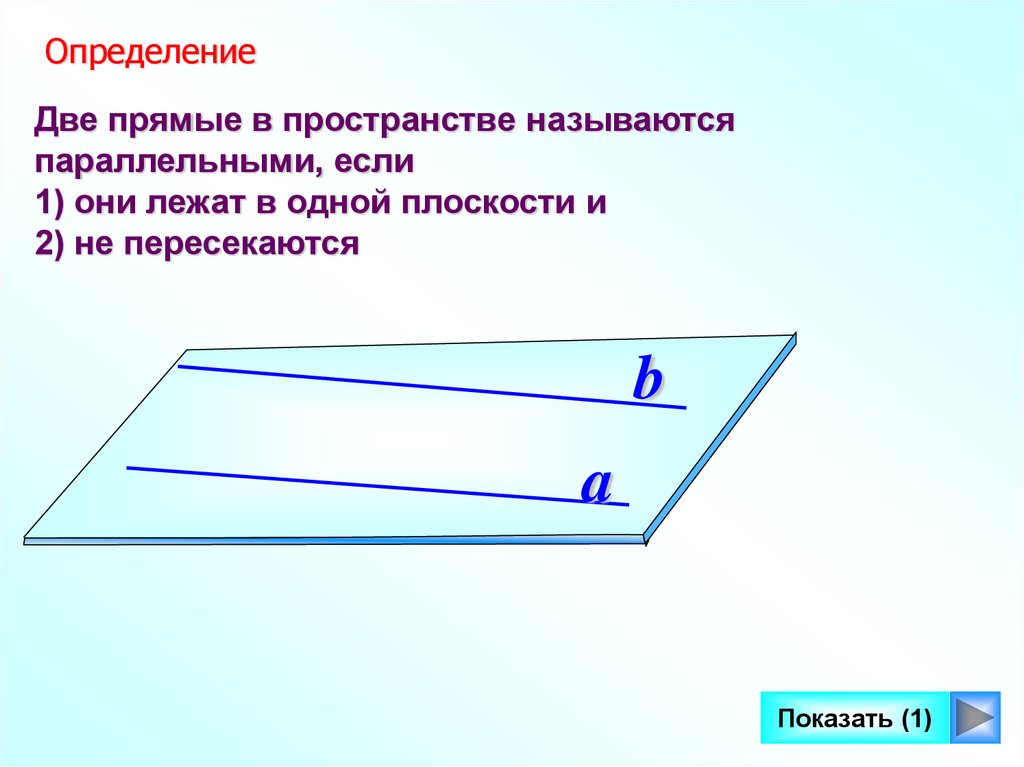
Определение
Две прямые в пространстве называются
параллельными, если
1) они лежат в одной плоскости и
2) не пересекаются
b
a
Показать (1)
5

6.

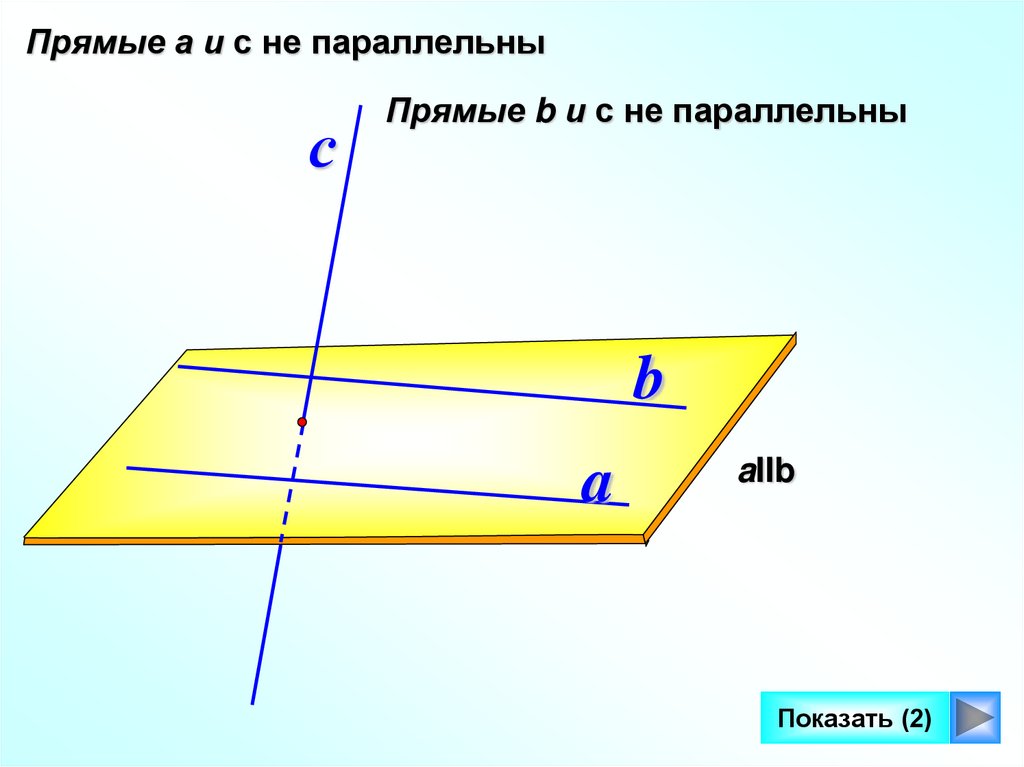
Прямые а и с не параллельны
с
Прямые b и с не параллельны
b
a
aIIb
Показать (2)
6

7.

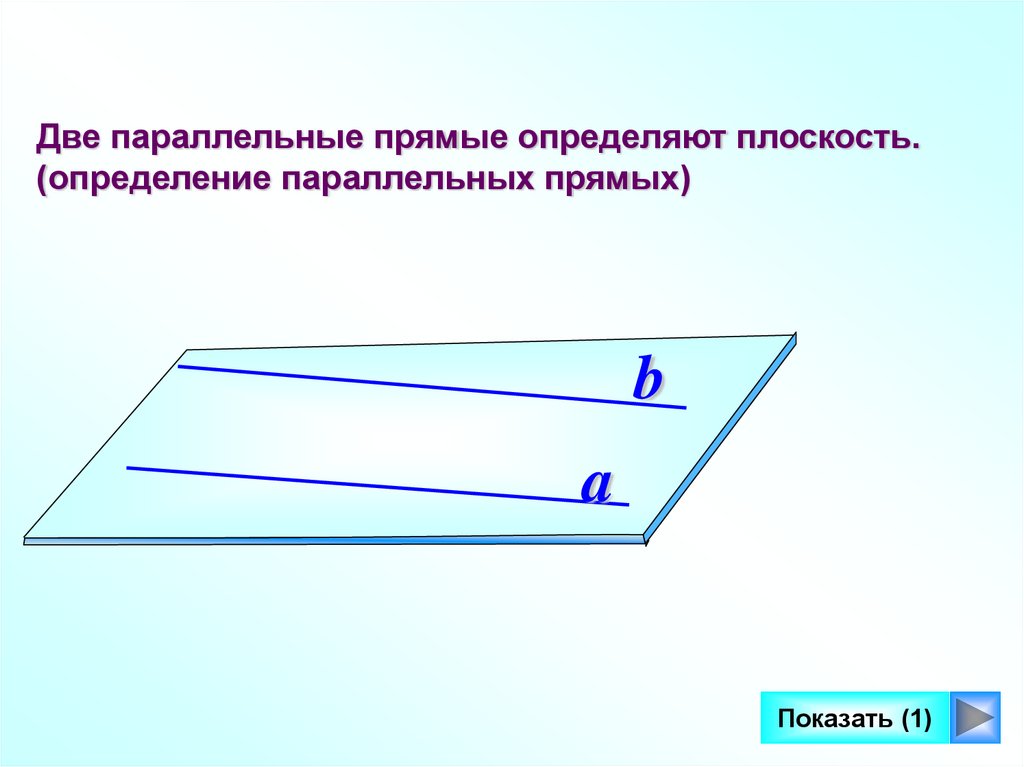
Две параллельные прямые определяют плоскость.
(определение параллельных прямых)
b
a
Показать (1)
7

8.

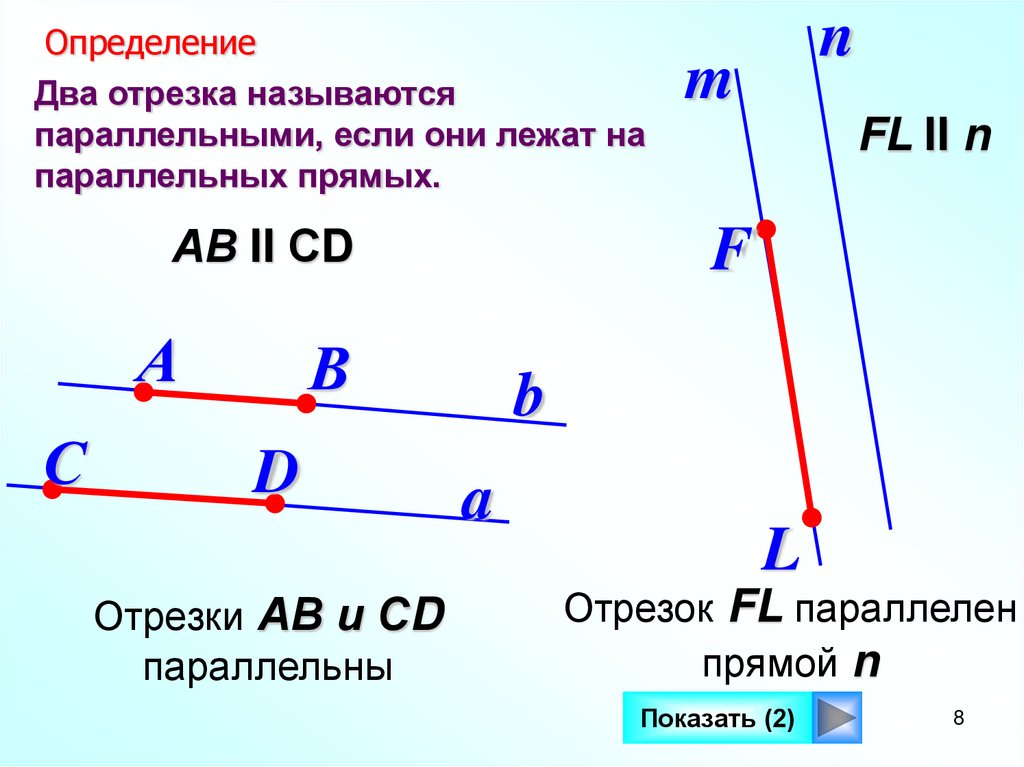
Определение
Два отрезка называются
параллельными, если они лежат на
параллельных прямых.
АВ II СD
А
С
Отрезки АВ и СD
параллельны
m
FL II n
F
В
D
n
b
a
L
Отрезок FL параллелен
прямой n
Показать (2)
8

9.

№ 17.
Точки М, N, P и Q – середины отрезков BD, CD, AB и АС.
РMNQP - ?
D
M
N
В
А
P
Q
С
9

10.

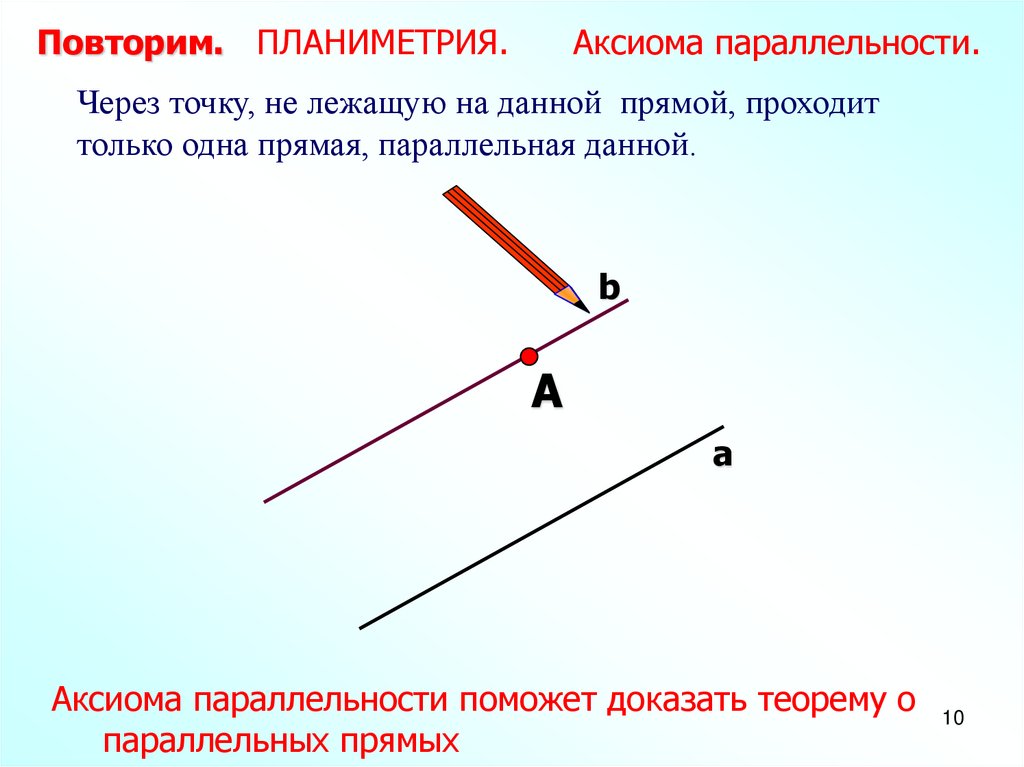
Повторим. ПЛАНИМЕТРИЯ.
Аксиома параллельности.
Через точку, не лежащую на данной прямой, проходит
только одна прямая, параллельная данной.
b
А
а
Аксиома параллельности поможет доказать теорему о
параллельных прямых
10

11.

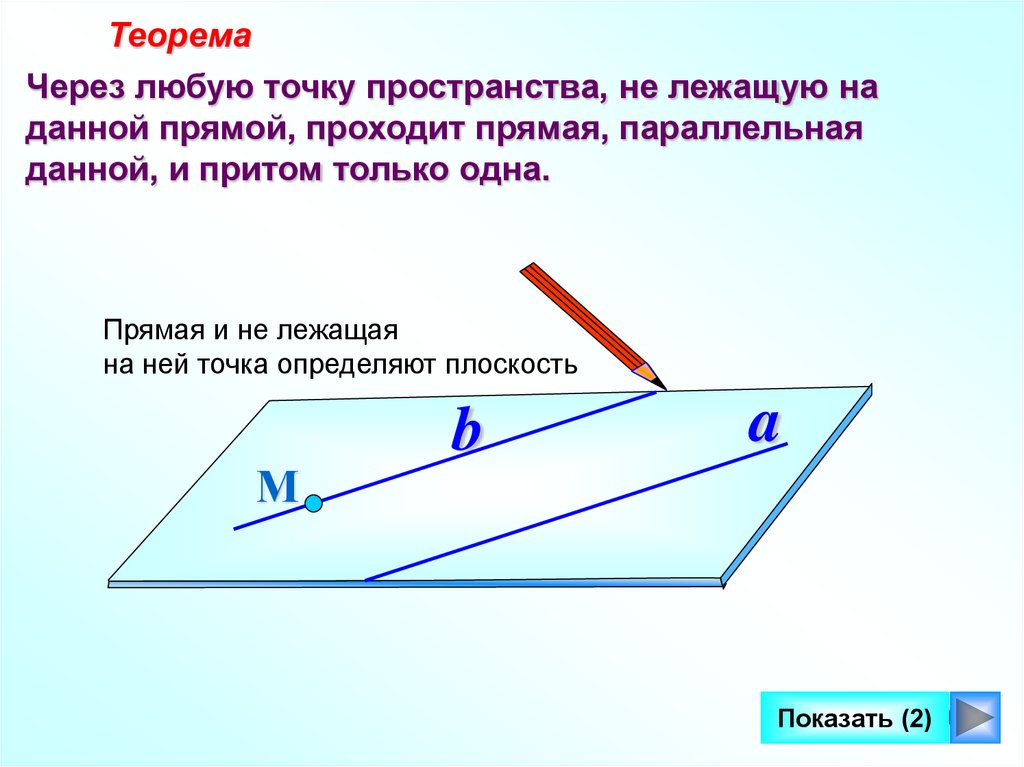
Теорема
Через любую точку пространства, не лежащую на
данной прямой, проходит прямая, параллельная
данной, и притом только одна.
Прямая и не лежащая
на ней точка определяют плоскость
М
b
a
Показать (2) 11

12.

Повторим.
Следствие из аксиомы параллельности.
b
c
а
Если прямая пересекает одну из двух
параллельных прямых, то она
пересекает и другую.
aIIb, c b
c
a
Это следствие из аксиомы параллельности поможет
доказать лемму о параллельных прямых
12

13.

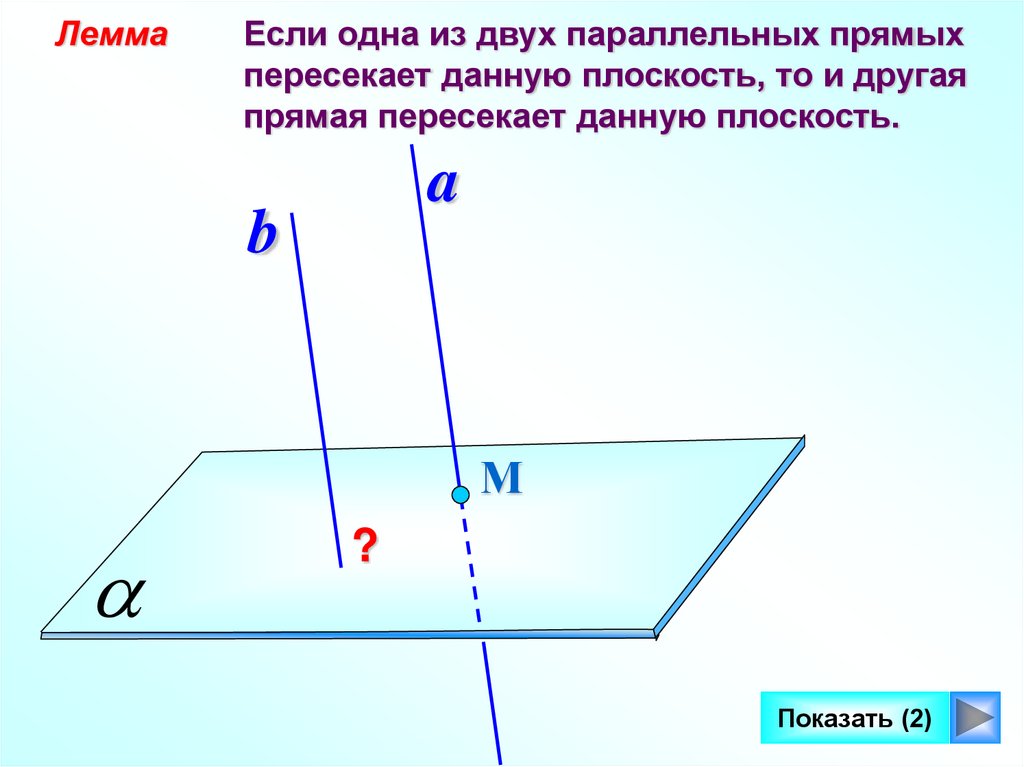
Лемма
Если одна из двух параллельных прямых
пересекает данную плоскость, то и другая
прямая пересекает данную плоскость.
a
b
М
?
Показать (2) 13

14.

Плоскости
и имеют общую
точку М, значит они пересекаются
по прямой (А3)
a
b
р
М
N
Прямая р лежит в плоскости
и пересекает прямую а в т. М.
Поэтому она пересекает и
параллельную ей прямую b
в некоторой точке N.
, поэтому N – точка
Прямая р лежит также в плоскости
плоскости .
Значит, N – общая точка прямой b и
плоскости .
14

15.

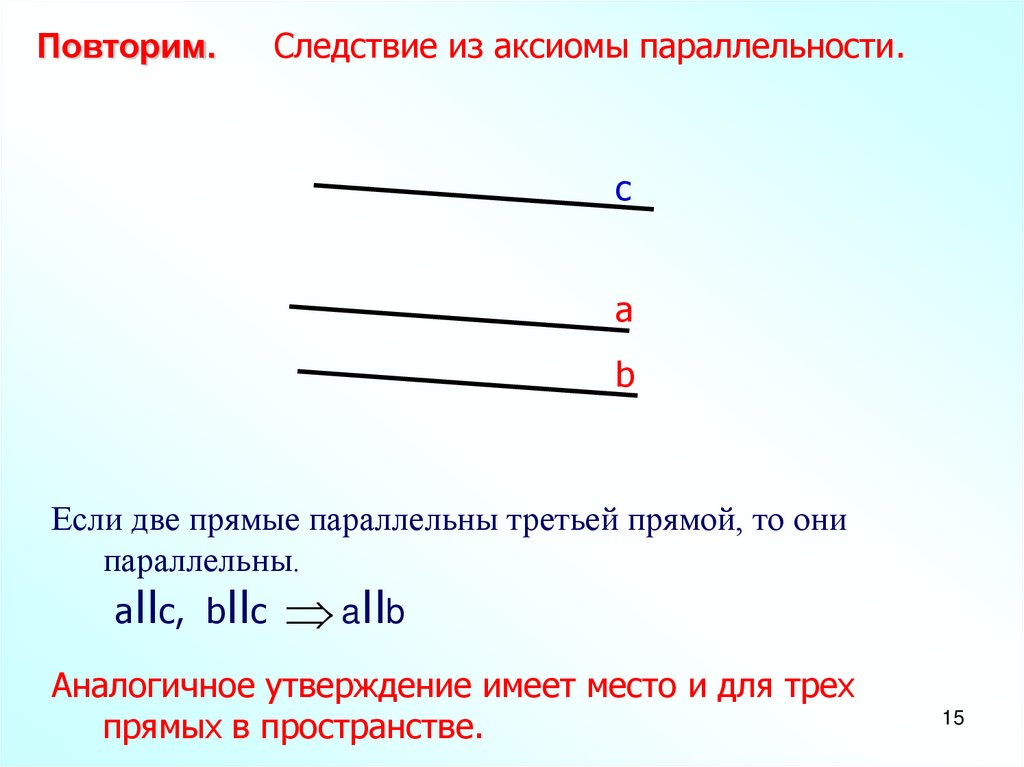
Повторим.
Следствие из аксиомы параллельности.
с
а
b
Если две прямые параллельны третьей прямой, то они
параллельны.
aIIс, bIIс aIIb
Аналогичное утверждение имеет место и для трех
прямых в пространстве.
15

16.

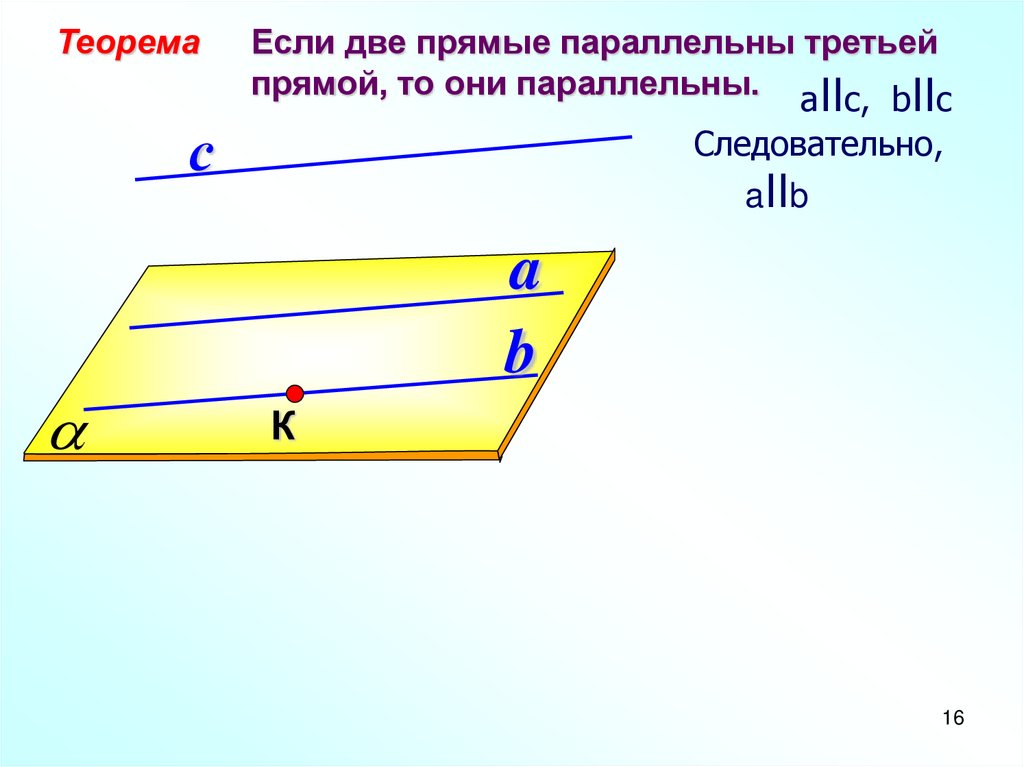
Теорема
с
Если две прямые параллельны третьей
прямой, то они параллельны. aIIс, bIIс
Следовательно,
aIIb
a
b
К
16

17.

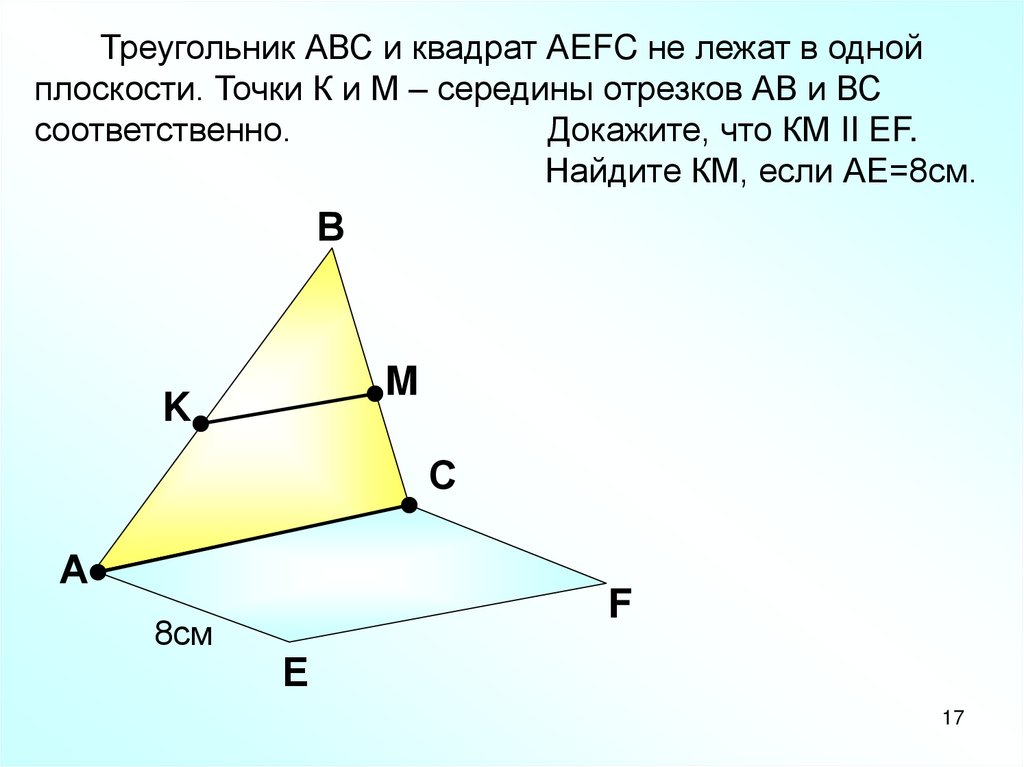
Треугольник АВС и квадрат АEFC не лежат в одной
плоскости. Точки К и М – середины отрезков АВ и ВС
соответственно.
Докажите, что КМ II EF.
Найдите КМ, если АЕ=8см.
В
M
K
С
А
8см
F
Е
17

18.

19.

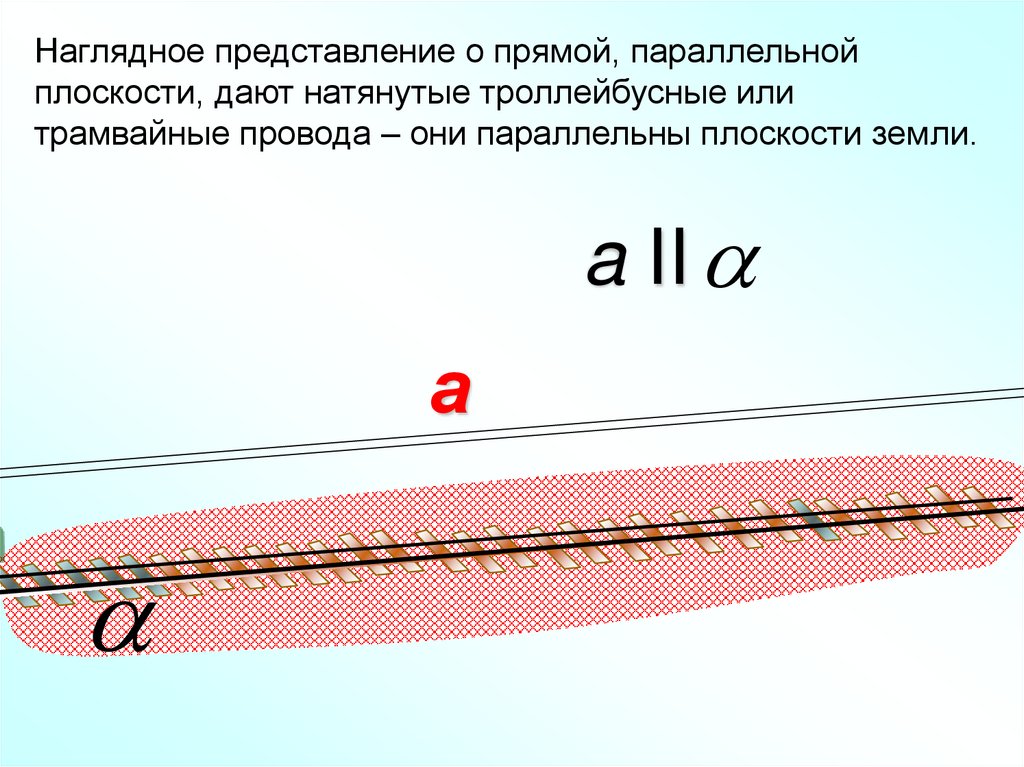
Наглядное представление о прямой, параллельной
плоскости, дают натянутые троллейбусные или
трамвайные провода – они параллельны плоскости земли.
a II
а

20.

а

21.

а
b

22.

Назовите прямые, параллельные данной плоскости
С1
D1
А1
В1
D
А
С
В

23.

Теорема
Если прямая не лежащая в данной плоскости,
параллельна какой-нибудь прямой, лежащей в этой
плоскости, то она параллельна этой плоскости.
a
b
Дано: a II b, b
Следовательно
a II

24.

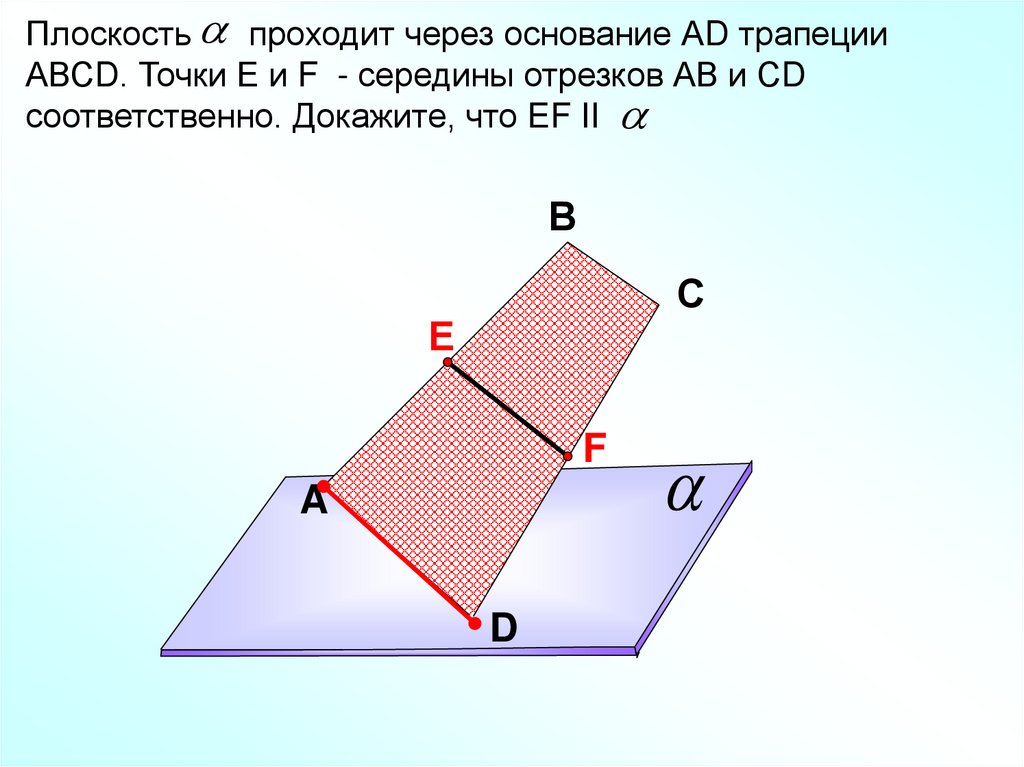
Плоскость проходит через основание АD трапеции
АВСD. Точки Е и F - середины отрезков АВ и СD
соответственно. Докажите, что EF II
В
С
Е
F
A
D

25.

Плоскость проходит через сторону АС треугольника АВС.
Точки D и E - середины отрезков АВ и BC соответственно.
Докажите, что DE II
В
D
E
A
С

26.

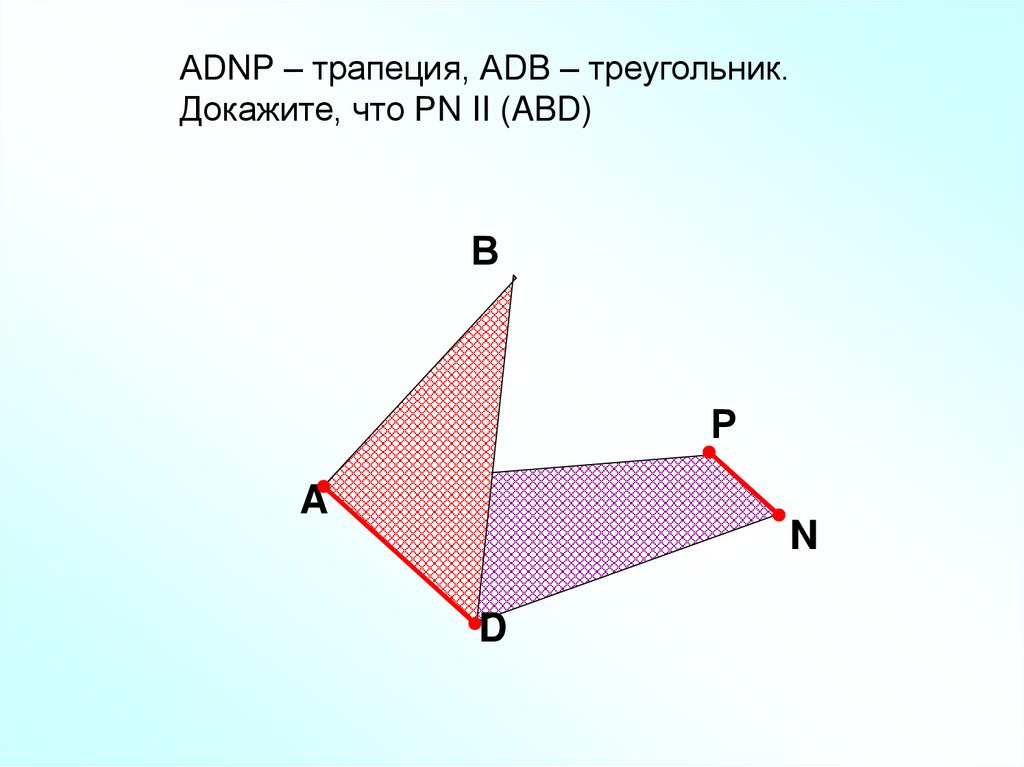
АDNP – трапеция, АDB – треугольник.
Докажите, что РN II (ABD)
В
Р
A
N
D

27.

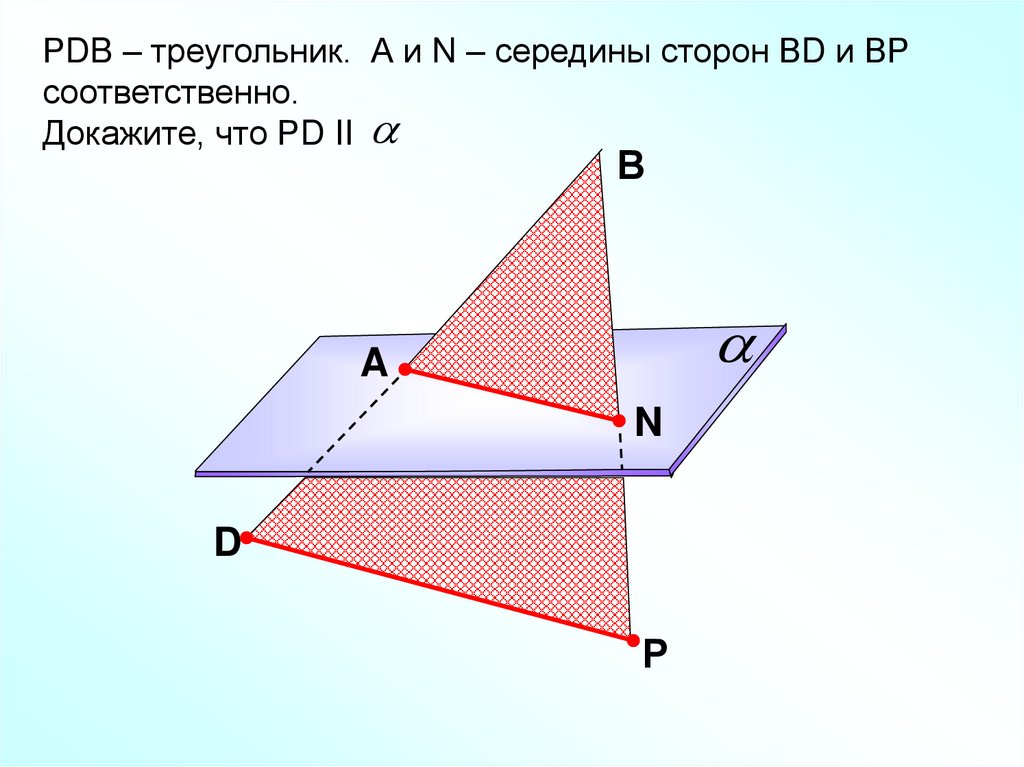
РDB – треугольник. А и N – середины сторон ВD и ВР
соответственно.
Докажите, что РD II
В
A
N
D
Р

28.

ДОМАШНЕЕ ЗАДАНИЕ:
Повторить( выучить теоремы и
леммы), решить задачи на
следующем слайде

29.

Плоскость проходит
через основание АD
трапеции АВСD. Точки Е
и F - середины отрезков
АВ и СD соответственно.
Докажите, что EF II
Плоскость проходит через
сторону АС треугольника
АВС. Точки D и E - середины
отрезков АВ и BC
соответственно.
Докажите, что DE II
В
В
D
E
A
С
Е
F
A
С
D