Теоретическая механика. Колебания материальной точки

1. Теоретическая механика

Курс лекций для студентов электромеханического
факультета
Лектор
Иваночкин Павел Григорьевич
доктор технических наук, профессор

2.

3.

y
O
x k x 0
2
x(t)
F
F c x ; m x F ; m x cx 0 m
круговая
c
c
2
c
частота
x
x
0
;
k
;
k
x
m
колебаний
m
m
– дифференциальное уравнение свободных колебаний материальной точки.
t
k 0; k i;
Основная форма
x C 1 k sin kt C 2 k cos kt .
общего решения: x C 1 cos kt C 2 sin kt
Определение констант: Начальные условия: при t 0 : x x0 , x
v0 .
x0 C 1 C 2 0 ;
v0
C 1 x0 ; C 2 k .
v0 C 1 k 0 C 2 k ;
Решение ищем в виде:
x e ;
Частное решение дифференциального уравнения
свободных колебаний материальной точки в
основной форме:
2
2
v0
x x0 cos kt sin kt
k

4.

x k x 0
2
Амплитудная форма
общего решения:
– дифференциальное уравнение свободных колебаний материальной точки.
Решение ищем в виде:
t
k 0; k i;
x e ;
2
2
x A sin kt или x A sin cos kt A cos sin kt .
x C 1 cos kt C 2 sin kt
C 1 A sin ; C 2 A cos .
2
0
2
v
А – амплитуда колебаний: A C C x
;
k
C 1 kx0
α – начальная фаза колебаний (изменяется в пределах [0,2π]): tg
;
C2
v0
2
1
2
2
Частное решение дифференциального уравнения
свободных колебаний материальной точки в
амплитудной форме:
2
0
v
kx0
x x
sin kt arctg
k
v0
2
0
2
0
2

5.

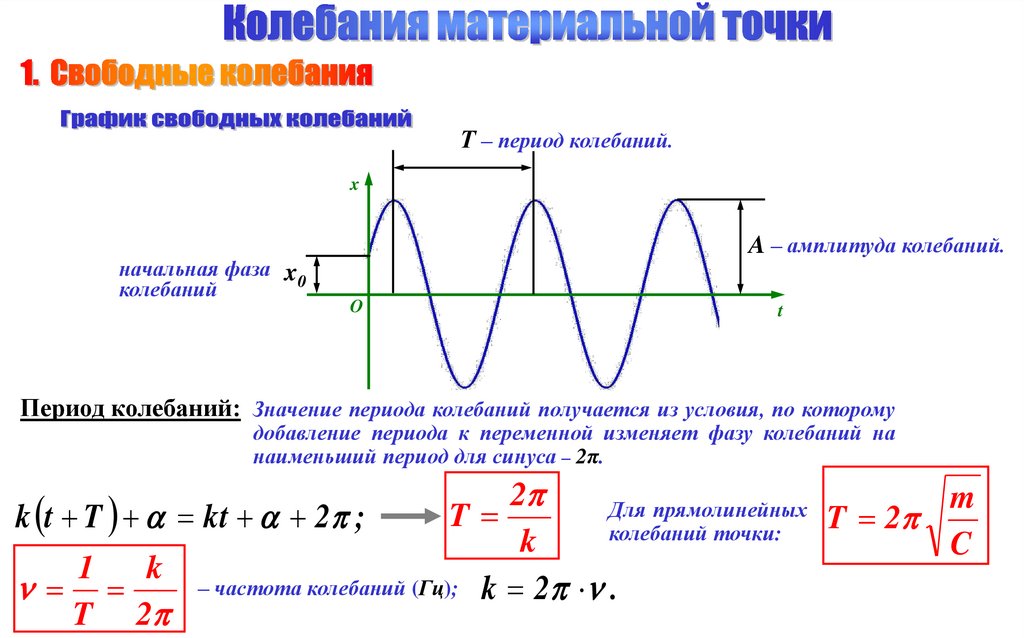
Т – период колебаний.
x
начальная фаза x0
колебаний
A – амплитуда колебаний.
O
t
Период колебаний: Значение периода колебаний получается из условия, по которому
добавление периода к переменной изменяет фазу колебаний на
наименьший период для синуса – 2π.
2
m
Для
прямолинейных
T
k t T kt 2 ;
T 2
колебаний точки:
k
C
1
k
– частота колебаний (Гц); k 2 .
T 2

6.

A
F
B
C
P
x
Пружина АВ, закрепленная одним концом в точке А, имеет жесткость с =
19,6 н/м. В некоторый момент к нижнему концу В недеформированной пружины
подвешивают гирю С массой m = 0.1 кг и отпускают ее без начальной скорости.
Найти уравнение движения гири, амплитуду и период ее колебаний пренебрегая
массой пружины.
Решение: ma P F ;
mx mg F ; mx mg cx ; k c m ;
x k 2 x g – дифференциальное уравнение движения гири.
g mg
x x1 x2 ;
частное решение неоднородного дифуравнения: x2 2
;
2
y
c
1 k x1 0 ; k
общее решение однородного дифуравнения: x
характеристическое уравнение: 2 k 2 0
ki ;
x1 C1 cos kt C2 sin kt .
0 0.
начальные условия: при t 0 : x0 0 ;x
mg
определение
C1 mg c ;
x C1 cos kt C 2 sin kt
произвольных
c
C 2 0.
постоянных:
x C1k sin skt C2 k cos kt
mg
mg mg
x
cos
t
c
c
c

7.

Пружина АВ, закрепленная одним концом в точке А, имеет жесткость с =
19,6 н/м. В некоторый момент к нижнему концу В недеформированной пружины
подвешивают гирю С массой m = 0.1 кг и отпускают ее без начальной скорости.
Найти уравнение движения гири, амплитуду и период ее колебаний пренебрегая
массой пружины.
Решение: ma P F . В положении статического равновесия: 0 P F ;
A
F c ст
F
F
B
C
mx mg F ; mx mg c x ст ;
начало
движения
статическая
ст деформация
λ
x
P
P
x
ст P c mg c
положение
статического
равновесия
y
x+λст
деформация
пружины
x mg k 2 x mg ;
x k x 0
2
k c m 14 ;
– дифференциальное уравнение
движения гири.
Характеристическое уравнение: 2 k 2 0
Общее решение однородного дифуравнения:
ki .
x C 1 cos kt C 2 sin kt

8.

Пружина АВ, закрепленная одним концом в точке А, имеет жесткость с =
19,6 н/м. В некоторый момент к нижнему концу В недеформированной пружины
подвешивают гирю С массой m = 0.1 кг и отпускают ее без начальной скорости.
Найти уравнение движения гири, амплитуду и период ее колебаний пренебрегая
массой пружины.
Решение:
A
x C 1 cos kt C 2 sin kt x C1k sin skt C2 k cos kt ;
0 0.
Начальные условия: при t 0 : x0 ст ; x
Определение произвольных постоянных: C1 ст 0 ,05 ; C 2 0.
начало
движения
F
λст статическая
деформация
B
x
C
P
x
положение
статического
равновесия
y
x+λст
деформация
пружины
x 0.05 cos 14 t м – уравнение движения гири.
Амплитуда колебаний:
A
Период колебаний:
T 2 k 0.45 c .
Ответ:
2
2
C 1 C 2 0.05 м .
x 0.05 cos 14 t м ; A 0.05 м ; T 0.45 c .

9.

y
O
F c x ; R x ; m x R F ; m
x(t)
F
c
c
2
x x
2
n
;
x
x
0
;
k
;
R
m
m
m
m
R
R
x 2 nx k x 0
2
Решение ищем в виде:
t
x e ;
– дифференциальное уравнение затухающих
колебаний материальной точки.
2 n k 0 ;
2
2
Три случая решения дифференциального уравнения:
n k;
2. Предельный случай:
n k;
3. Случай большого сопротивления: n k ;
1. Случай малого сопротивления:
n n k ;
2
2

10.

n k
1 , 2 n k1 i , где
k1 k n
2
2
c
m
2
2m
круговая частота
Затухающих колебаний
C 1 cos k1t C 2 sin k1t
nt
nt
x ne C 1 cos k1 t C 2 sin k1 t e C 1 k1 sin k1 t C 2 k1 cos k1 t .
Основная форма общего решения:
x e
nt
Определение констант: Начальные условия: при t 0 : x x0 , x
v0 .
x0 1 C 1 C 2 0 ;
v0 nC 1 C 2 k1 ;
Частное
решение
дифференциального уравнения затухающих
колебаний материальной точки в
основной форме:
1
C 1 x0 ; C 2 v0 nx0 .
k1
x e
nt
1
x
cos
k
t
v
nx
sin k1t
0
1
0
0
k1

11.

n k
Амплитудная форма
общего решения:
или
x e
nt
x Ae
nt
sin k1t
A sin cos k1t A cos sin k1t .
x e nt C 1 cos k1t C 2 sin k1t
v0 nx0
x
;
C 1 A sin ;
C 2 A cos .
2
Амплитуда колебаний: A
C C
2
1
2
2
2
0
2
1
k
α – начальная фаза колебаний (изменяется в пределах [0,2π]):
Частное решение дифференциального уравнения затухающих колебаний материальной
точки в амплитудной форме:
C1
x0 k1
tg
;
C 2 v0 nx0
v0 nx0
x
sin kt arctg
2
x
2
0
2
1
k
x0 k1
v0 nx0

12.

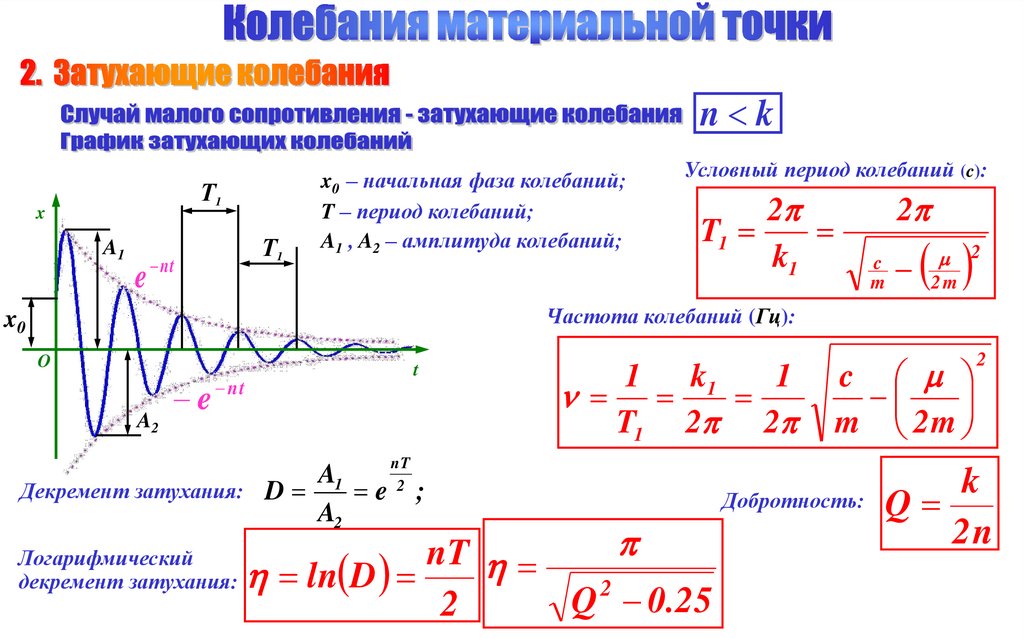
n k
Т1
x
A1
e
Т1
nt
x0 – начальная фаза колебаний;
T – период колебаний;
A1 , A2 – амплитуда колебаний;
Условный период колебаний (c):
2
T1
k1
2
c
m
2
2m
Частота колебаний (Гц):
x0
O
A2
e
t
nt
Декремент затухания:
Логарифмический
декремент затухания:
A1
D
e
A2
nT
2
1
k1
1
T1 2 2
;
nT
ln D
2
Q 0.25
2
c
m 2m
2
k
Добротность: Q
2n

13.

n k
1 , 2 n . Общее решение: x e nt C 1 t C 2 x ne nt C 1 t C 2 e ntC 1 .
Определение констант:
Начальные условия: при
x0 1 C 1 0 C 2 ;
v0 nC 2 C 1 ;
t 0 : x x0 , x v0 .
C 2 x0 ;
C 1 v0 nx0 .
Частное решение дифференциального
уравнения
затухающего
движения
материальной точки :
x e
nt
v0 nx0 t x0
x
v0 > 0
v0 = 0
x0
t
O
v0 < 0

14.

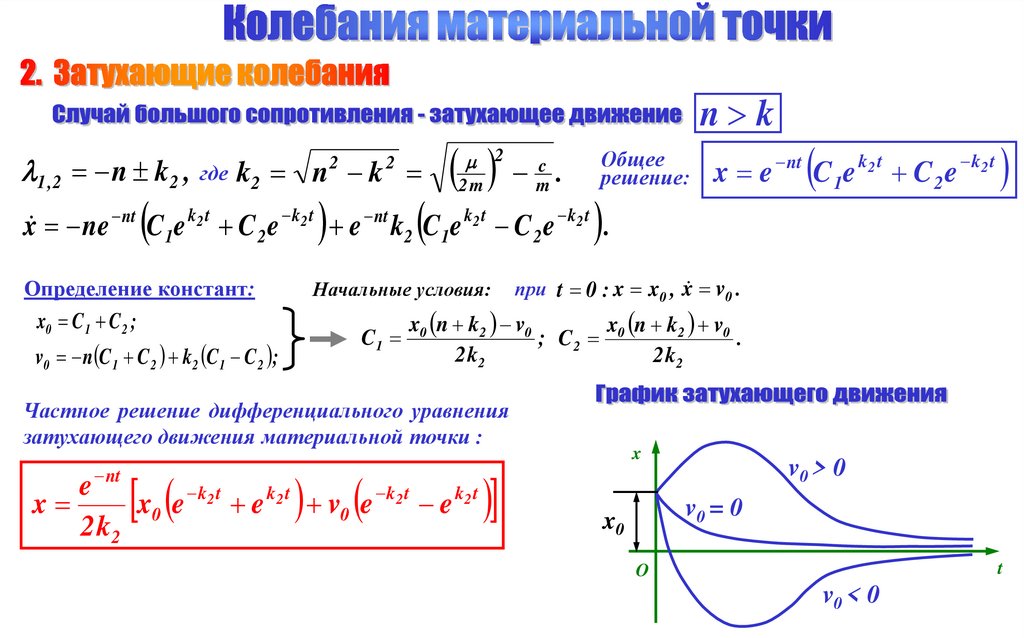
1 , 2 n k2 , где k2 n k
2
x ne
nt
2
n k
2
c
.
2m
m
Общее
решение:
C e C e e k C e C e .
k2 t
k2 t
1
2
Определение констант:
x0 C 1 C 2 ;
nt
v0 n C 1 C 2 k2 C 1 C 2 ;
1
1
C2e
k2 t
2
Начальные условия:
при t 0 : x x0 , x v0 .
x0 n k2 v0
x n k2 v0
C1
; C2 0
.
2 k2
2 k2
Частное решение дифференциального уравнения
затухающего движения материальной точки :
nt
C e
k2 t
k2 t
k2 t
2
x e
nt
e
k2 t
k2 t
k2 t
k2 t
x
x0 e
e v0 e
e
2 k2
x
v0 > 0
v0 = 0
x0
t
O
v0 < 0

15.

A
Пластина C массой m = 0.1 кг , подвешенная на пружине АВ, движется между полюсами
магнита. Вследствие вихревых токов движение тормозится силой, пропорциональной скорости. Сила
сопротивления движению R = fФ2v Н, где f = 0,001, Ф = 10√5 [Вб] — магнитный поток между
полюсами магнита. В начальный момент скорость пластинки равна нулю и пружина не растянута;
жесткость пружины с = 19,6 н/м.
Найти уравнение движения пластины.
Решение: ma P F R ; mx
mg F R ; mx mg c x ст x ;
k c m 14 c 1 ; 2 n m 5 c 2 ; ст mg c 0.05 м .
x 2 nx k x 0 – дифференциальное уравнение движения пластины.
2
B
CR
F
положение
статического
равновесия
y
Характеристическое уравнение:
x
n k1i ;
k1 k 2 n 2 13 .77 c 1 .
Общее решение:
Скорость:
P
2 2 n k 2 0
x e
nt
C 1 cos k1t C 2 sin k1t .
x ne nt C 1 cos k1 t C 2 sin k1 t e nt C 1 k1 sin k1 t C 2 k1 cos k1 t .

16.

A
Пластина C массой m = 0.1 кг , подвешенная на пружине АВ, движется между полюсами
магнита. Вследствие вихревых токов движение тормозится силой, пропорциональной скорости. Сила
сопротивления движению R = fФ2v Н, где f = 0,001, Ф = 10√5 [Вб] — магнитный поток между
полюсами магнита. В начальный момент скорость пластинки равна нулю и пружина не растянута;
жесткость пружины с = 19,6 н/м.
Найти уравнение движения пластины.
Решение:
x e nt C 1 cos k1t C 2 sin k1t
R
B
C
x
F
положение
статического
равновесия
P
x ne nt C 1 cos k1 t C 2 sin k1 t e nt C 1 k1 sin k1 t C 2 k1 cos k1 t .
0 0.
Начальные условия: при t 0 : x0 ст 0 ,05 м ; x
y
C1 0.05 ;
n
C2 ст 0.0091.
k1
2 .5 t
0.05 cos 13.77 t 0.0091 sin 13.77 t м .
x e
Определение
произвольных
постоянных:
Ответ: x e 2.5 t 0.05 cos 13.77 t 0.0091 sin 13.77 t м .

17.

18.

y
O
x(t)
F
x
HH
m x F H ;
F c x;
H N sin pt ;
m x cx N sin pt m
Дифференциальное уравнение вынужденных колебаний материальной точки:
x k x h sin pt
2
x x1 x 2 ;
x 1 C 1 cos kt C 2 sin kt ;

19.

x 2 B sin pt ;
2
x 2 Bp cos pt ; x 2 Bp sin pt ;
2
2
Bp Bk h sin pt 0 ;
B 2 h 2 ; x 2 2 h 2 sin pt ;
p k
Основная форма
общего решения:
k p
k p
x C 1 cos kt C 2 sin kt k 2 h p 2 sin pt
x C 1k sin kt C 2 k cos kt k 2 p 2 cos pt .
hp
Определение констант:
при t 0 : x x0 , x v0 .
Начальные условия:
x0 C 1 k 2 h p 2 sin ;
C 1 x0 k 2 h p 2 sin ;
v0
hp
C 2 k k k 2 p 2 cos .
v0 C 2 k k 2 p 2 cos ;
Частное решение дифференциального уравнения свободных колебаний материальной точки в основной форме:
hp
x
x0 k 2 h p 2 sin
cos kt
v0
hp
k k 2 p 2 cos
k
sin kt k 2 h p 2 sin pt

20.

x 2 B sin pt ;
2
x 2 Bp cos pt ; x 2 Bp sin pt ;
2
2
Bp Bk h sin pt 0 ;
B 2 h 2 ; x 2 2 h 2 sin pt ;
p k
Амплитудная форма
общего решения:
k p
k p
x A sin kt k 2 h p 2 sin pt
Амплитуда собственных колебаний:
A
С 12 С 22
x0 k 2 h p 2 sin
2
2
1
hp
2 v0 k 2 p 2 cos .
k
C1
x0 k 2 p 2 h sin
Начальная фаза собственных колебаний: arctg
arctg k v k 2 p 2 hp cos .
0
C2
Частное решение дифференциального уравнения свободных колебаний материальной точки в амплитудной форме:
x
x
0
h
k 2 p2
sin
2
2
1
x0 k 2 p 2 h sin
hp
2 v0 k 2 p 2 cos sin kt arctg k v k 2 p 2 hp cos k 2 h p 2 sin pt
0
k

21.

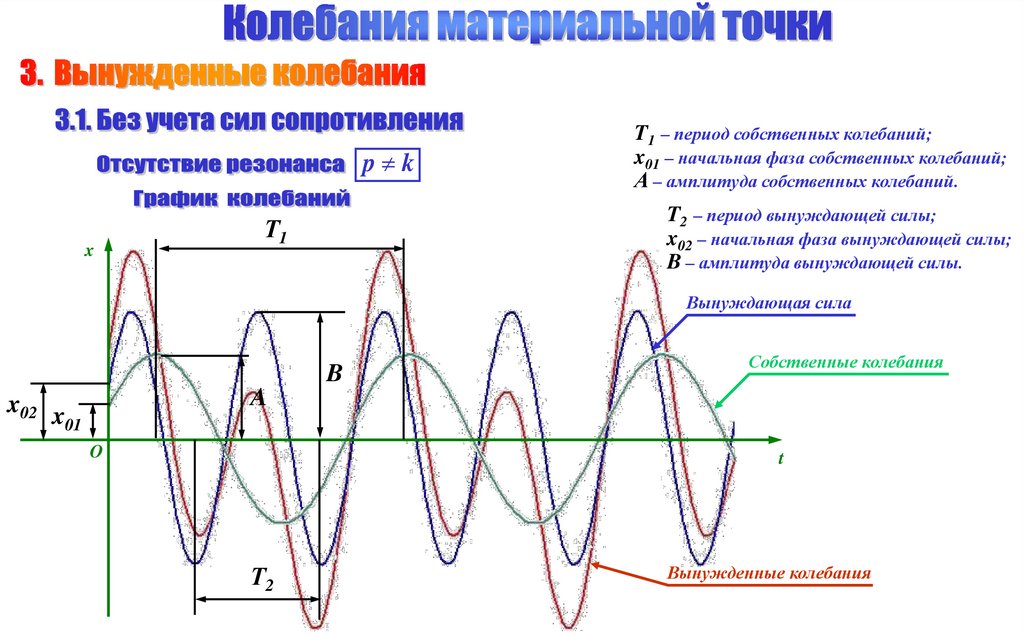
p k
x
T1 – период собственных колебаний;
x01 – начальная фаза собственных колебаний;
А – амплитуда собственных колебаний.
T2 – период вынуждающей силы;
x02 – начальная фаза вынуждающей силы;
B – амплитуда вынуждающей силы.
Т1
Вынуждающая сила
B
x02 x
Собственные колебания
A
01
O
t
Т2
Вынужденные колебания

22.

x 2 Bt cos pt ;
p k
x 2 B cos pt Bpt sin( pt ); x 2 2 Bp sin pt Bp 2 t cos pt ;
B 2hp ; x 2 2htp cos pt 2htp sin pt 2 ;
2 Bp h sin pt 0 ;
Основная форма
общего решения:
x C 1 cos kt C 2 sin kt 2htp sin pt 2
x C 1 k sin kt C 2 k cos kt 2hp sin pt 2 ht2 cos pt 2 .
Определение констант:
x0 C 1 ;
v0 C 2 k 2hp cos ;
Начальные условия:
при t 0 : x x0 , x v0 .
C 1 x0 ;
C 2 vk0 2 hpk cos .
Частное решение дифференциального уравнения свободных колебаний материальной точки в основной форме:
x x0 cos kt
v0
k
h
2 pk
cos sin kt 2htp sin pt 2

23.

x 2 Bt cos pt ;
p k
x 2 B cos pt Bpt sin( pt ); x 2 2 Bp sin pt Bp 2 t cos pt ;
B 2hp ; x 2 2htp cos pt 2htp sin pt 2 ;
2 Bp h sin pt 0 ;
Амплитудная форма
общего решения:
x A sin kt 2htp sin pt 2
Амплитуда собственных колебаний:
A
Начальная фаза собственных колебаний:
2
2
С1 С 2
2
x0 k12
v0 2hp cos
.
2
C1
0
arctg
arctg 2 p 2v0pk h x cos
.
C2
Частное решение дифференциального уравнения свободных колебаний материальной точки в амплитудной форме:
x x
2
0
1
k2
v
0
h
2p
cos
sin kt arctg
2
2 pk x0
2 p v0 h cos
sin pt
ht
2p
2

24.

p k
Зависимость амплитуды колебаний от
круговой частоты возмущающей силы
x
Вынужденные колебания
Возмущающая сила
h
при p k или
2
2
k p
h
B
1
где
B 2.
2
p
B 1 2
k
k
B
B
B
x 2 ht 2 p
Собственные колебания
1
0
O
t
p k
p k
p k
p
k
При p k
Зависимость сдвига фаз колебаний от
круговой частоты возмущающей силы
2
x 2 ht 2 p
0
p k
p k
p k
p
k
ht
B
.
2p

25.

A
Магнит C массой m = 0.1 кг подвешен на пружине АВ жесткостью с = 19,6 н/м движется в поле
соленоида, по катушке которого идет переменный ток i = 20sin(8πt). Ток идет с момента t = 0,
втягивая стержень в соленоид; до этого момента магнит висел неподвижно. Сила взаимодействия
между катушкой и магнитом T = 0.016πi Н.
Определить уравнение дальнейшего движения магнита.
Решение:
B
ma P F T ; mx mg c x ст 0.32 sin 8 t ;
1
mx mg F T ; k c m 14 c ; ст mg c 0.05 м .
1
p 8 25.12 c ; h 0.32 m 10.05 м.
C
x k x h sin pt – дифференциальное уравнение движения магнита.
2
F
y
x x1 x 2 ;
x 1 C 1 cos kt C 2 sin kt ;
p k x 2 2 h 2 sin pt ;
x
0
.
023
sin
8
t
2
k p
положение
статического
равновесия
T P
x
– вынужденные
колебания
магнита.

26.

A
Магнит C массой m = 0.1 кг подвешен на пружине АВ жесткостью с = 19,6 н/м движется в поле
соленоида, по катушке которого идет переменный ток i = 20sin(8πt). Ток идет с момента t = 0,
втягивая стержень в соленоид; до этого момента магнит висел неподвижно. Сила взаимодействия
между катушкой и магнитом T = 0.016πi Н.
Определить уравнение дальнейшего движения магнита.
Решение:
B
ma P F T ; mx mg c x ст 0.32 sin 8 t ;
1
mx mg F T ; k c m 14 c ; ст mg c 0.05 м .
1
p 8 25.12 c ; h 0.32 m 10.05 м.
C
x k x h sin pt – дифференциальное уравнение движения магнита.
2
F
y
x x1 x 2 ;
x 1 C 1 cos kt C 2 sin kt ;
p k x 2 2 h 2 sin pt ;
x
0
.
023
sin
8
t
2
k p
положение
статического
равновесия
T P
x
– вынужденные
колебания
магнита.

27.

y
O
x(t)
F
x
R HH R
R
F c x ; H N sin pt ; R x ;
m x F H R ;
m x x cx N sin pt m
c
c
N
2
x x x 0 , где k ; 2 n ; h .
m
m
m
m
m
Дифференциальное уравнение вынужденных колебаний материальной точки с учетом сил
сопротивления движению:
x 2 nx k x h sin pt x x 1 x 2 ;
2
Три случая общего решения однородного дифференциального уравнения:
1. Случай малого сопротивления
2. Предельный случай
n k : x1 e C 1 cos k1t C 2 sin k1t .
nt
C 1t C 2 .
x
e
n k: 1
3. Случай большого сопротивления n k :
nt
x1 e
nt
C e
1
k2 t
C2e
k2 t
.

28.

Дифференциальное уравнение вынужденных колебаний материальной точки с учетом сил
сопротивления движению:
x 2 nx k x h sin pt x x 1 x 2 ;
Частное решение неоднородного дифференциального уравнения: x 2 B sin pt ;
x 2 Bp cos pt ; x 2 Bp 2 sin pt ;
2
2
Bp sin pt 2 nBp cos pt Bk sin pt h sin pt ;
2
h sin pt h sin pt h sin cos pt h cos sin pt ;
B k p h cos sin pt 2 Bnp h sin cos pt 0 ;
B k p h cos 0 ; 2 Bnp h sin 0 ;
2
2
2
B
2
h
k p 4 n2 p 2
2
2 2
tg k 2 p 2 , 0
2 np
x2
h
k 2 p 4 n2 p 2
2 2
sin pt arctg k 2 p 2
2 np

29.

На пружине АВ жесткостью с = 19,6 н/м подвешены магнит C массой m = 0.05 кг ,
движущийся в поле соленоида, по катушке которого идет переменный ток i = 20sin(8πt) и
пластина D массой m = 0.05 кг, движущаяся между полюсами постоянного магнита.
Сила взаимодействия между катушкой соленоида и магнитом T = 0.016πi Н. Ток идет с
момента t = 0, втягивая стержень в соленоид.
Сила сопротивления движению пластины R = fФ2v Н, где f = 0,001, Ф = 10√5 [Вб] —
магнитный поток между полюсами магнита. В начальный момент магнит и пластину подвесили
к концу нерастянутой пружины и сообщили скорость v0 = 0,05 м/с , направленную вниз.
A
B
R
F
C
Определить уравнение дальнейшего движения магнита с пластиной.
Решение:
y
положение
статического
равновесия
P
DT
m m1 m2 0.1 кг ; k c m 14 c ; ст mg c 0.05 м .
1
fФ 0.5 ; 2 n m 5 c 2 ; p 8 25.12 c 1 ; h 0.32 m 10.05 м.
2
x 2 nx k x h sin pt – дифференциальное уравнение движения системы.
2
x
ma P F T R ; mx mg F T R ;
mx mg c x ст x 0.32 sin 8 t ;

30.

На пружине АВ жесткостью с = 19,6 н/м подвешены магнит C массой m = 0.05 кг ,
движущийся в поле соленоида, по катушке которого идет переменный ток i = 20sin(8πt) и
пластина D массой m = 0.05 кг, движущаяся между полюсами постоянного магнита.
Сила взаимодействия между катушкой соленоида и магнитом T = 0.016πi Н. Ток идет с
момента t = 0, втягивая стержень в соленоид.
Сила сопротивления движению пластины R = fФ2v Н, где f = 0,001, Ф = 10√5 [Вб] —
магнитный поток между полюсами магнита. В начальный момент магнит и пластину подвесили
к концу нерастянутой пружины и сообщили скорость v0 = 0,05 м/с , направленную вниз.
A
R
B F
Определить уравнение дальнейшего движения магнита с пластиной.
Решение:
y
C
x x1 x 2 ;
x 2 nx k x h sin pt
2
частное решение неоднородного дифуравнения: x 2 B sin pt
общее решение однородного дифуравнения:
P
T
D
x
;
x1 e C 1 cos k1 t C 2 sin k1 t .
2
2
2
2
1
k1 k n 14 2.5 13 .77 c ;
0 v0 0.05 м c .
Начальные условия: при t 0 : x0 ст 0 ,05 м ; x
– случай малого сопротивления n k :
nt

31.

На пружине АВ жесткостью с = 19,6 н/м подвешены магнит C массой m = 0.05 кг ,
движущийся в поле соленоида, по катушке которого идет переменный ток i = 20sin(8πt) и
пластина D массой m = 0.05 кг, движущаяся между полюсами постоянного магнита.
Сила взаимодействия между катушкой соленоида и магнитом T = 0.016πi Н. Ток идет с
момента t = 0, втягивая стержень в соленоид.
Сила сопротивления движению пластины R = fФ2v Н, где f = 0,001, Ф = 10√5 [Вб] —
магнитный поток между полюсами магнита. В начальный момент магнит и пластину подвесили
к концу нерастянутой пружины и сообщили скорость v0 = 0,05 м/с , направленную вниз.
A
R
B F
Определить уравнение дальнейшего движения магнита с пластиной.
Решение:
y
C
P
T
D
x
x2
h
k 2 p 4 n2 p 2
2 2
sin pt arctg k 2 p 2 0.022 sin 25.12 t 0.28 ;
2 np
x e nt C 1 cos k1 t C 2 sin k1 t 0.022 sin 25.12 t 0.28 ;
x ne nt C 1 cos k1 t C 2 sin k1 t k1e nt C 1 sin k1 t C 2 cos k1 t
0.022 25.12 cos 25.12 t 0.28 ;

32.

На пружине АВ жесткостью с = 19,6 н/м подвешены магнит C массой m = 0.05 кг ,
движущийся в поле соленоида, по катушке которого идет переменный ток i = 20sin(8πt) и
пластина D массой m = 0.05 кг, движущаяся между полюсами постоянного магнита.
Сила взаимодействия между катушкой соленоида и магнитом T = 0.016πi Н. Ток идет с
момента t = 0, втягивая стержень в соленоид.
Сила сопротивления движению пластины R = fФ2v Н, где f = 0,001, Ф = 10√5 [Вб] —
магнитный поток между полюсами магнита. В начальный момент магнит и пластину подвесили
к концу нерастянутой пружины и сообщили скорость v0 = 0,05 м/с , направленную вниз.
A
R
B F
Определить уравнение дальнейшего движения магнита с пластиной.
Решение:
y
C
P
T
D
x
Определение
произвольных
постоянных:
x e
2 .5 t
0.05 C1 0.022 sin 0.28 ;
0.05 nC1 k1C2 5.53 cos 0.28 ;
C1 0.044 ;
C2 0.043;
0.044 cos 13.77 t 0.043 sin 13.77 t 0.022 sin 25.12 t 0.28
Ответ: x e 2.5 t 0.044 cos 13.77 t 0.043 sin 13.77 t 0.022 sin 25.12 t 0.28

33.

Вынужденные
колебания
при
линейном
сопротивлении
являются
незатухающими. Амплитуда их постоянна как при отсутствии резонанса, так и
при резонансе.
Линейное сопротивление не влияет на частоту вынужденных колебаний,
которая совпадает с частотой возмущающей силы.
Вынужденные колебания как при линейном сопротивлении, так и при его
отсутствии не зависят от начальных условий.
Амплитуда вынужденных колебаний стремится к нулю с увеличением
относительной частоты возмущающей силы, причем при наличии линейного
сопротивления – быстрее.

34.

: m v P sin ; v l ; ; ml mg sin ;
O
φ
g
sin 0
l
l
n
τ
M
– дифференциальное уравнение движения
g
В случае малых колебаний ( sinφ ≈ φ ):
0
l
A sin kt
M0
P
k
A
2
T
g
2
– круговая частота колебаний;
l
k
– амплитуда колебаний;
– начальная фаза колебаний;
математического
маятника
–
не
интегрируется в элементарных функциях.
– общее
решение
дифференциального
уравнения
малых
колебаний
математического маятника .
l – период малых колебаний.
g
В случае обычных колебаний:
1 sin sin ...
T 2
l
g
T 2
l
g
1 2
2
1
A2
16
2 A
2
1 3 2
2 4
4 A
2
– колебания не являются гармоническими,
период колебаний зависит от амплитуды.
– приближенная формула вычисления периода негармонических колебаний
математического маятника.