Вынужленные колебания, затухающие колебания

1. ВЫНУЖЛЕННЫЕ КОЛЕБАНИЯ, ЗАТУХАЮЩИЕ КОЛЕБАНИЯ.

ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
ДИНАМИКА
ЛЕКЦИЯ 3

2. СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ

Начало отсчета – в положении
равновесия
lO
0
F
FC
x
l
F c l cx
l
FC x
Запишем ДУ движения точки
m x F FC m x cx x
ДУ свободных затухающих
колебаний
x 2bx k x 0
b / 2m k 2 c / m
2
2
Затухающие колебания

3. СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ

x 2bx k x 0
2
b / 2m k c / m
2
1. Случай малого сопротивления b k
bt
x e (C1 sin k1t C2 cos k1t )
bt
x Ae sin( k1t )
v x
Ae
bt
3
Затухающие колебания
( b sin( k1t ) k1 cos(k1t ))

4. СЛУЧАЙ МАЛОГО СОПРОТИВЛЕНИЯ

Используем начальные условия
x(0) x0
v(0) v 0
x0 A sin
v0 A( b sin k1 cos )
Получим постоянные интегрирования
A x (v 0 bx0 ) / k
2
0
2
2
1
tg x0 k1 /( v 0 bx0 )
k1 k 2 b 2
частота колебаний
T1 2 / k1 2 / k 2 b 2
период колебаний
4
Затухающие колебания

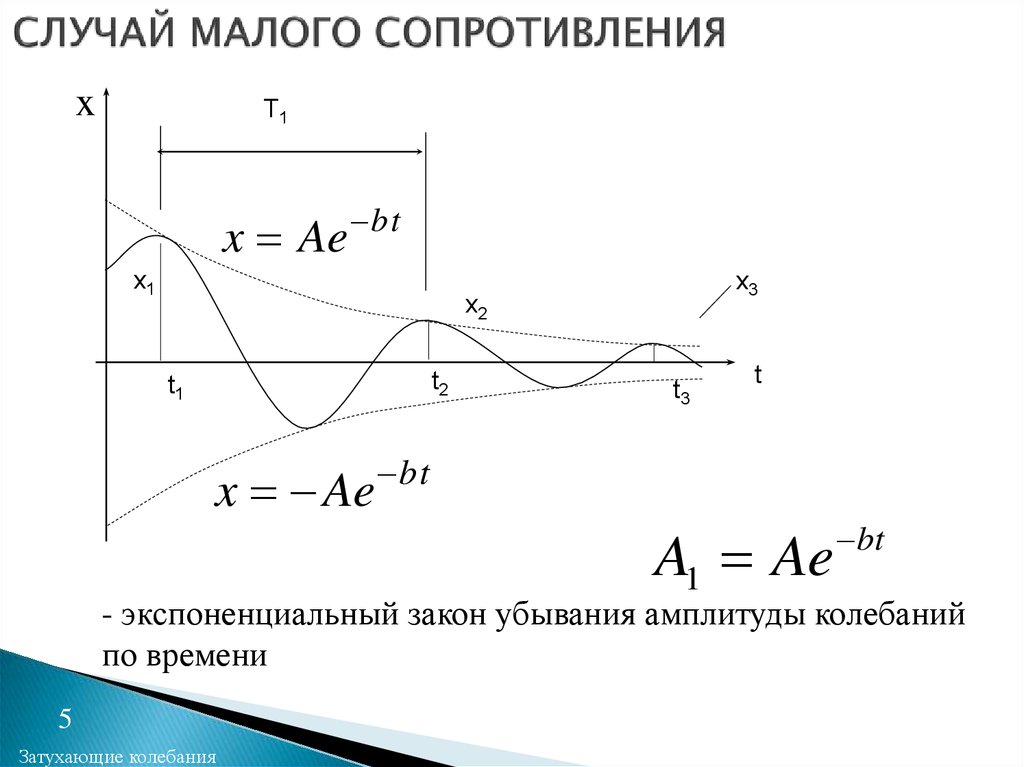
5. СЛУЧАЙ МАЛОГО СОПРОТИВЛЕНИЯ

x
T1
x Ae
bt
x1
x3
x2
t2
t1
t3
t
x Ae bt
A1 Ae
bt
- экспоненциальный закон убывания амплитуды колебаний
по времени
5
Затухающие колебания

6. СЛУЧАЙ МАЛОГО СОПРОТИВЛЕНИЯ

Выясним, как меняется амплитуда колебаний за один период
x n Ae
btn
sin( k1t n )
x n 1 Ae
btn 1
sin( k1t n 1 )
t n 1 t n T1
с учетом
получим
x n 1 / x n e
bT1
Амплитуда колебаний будет убывать по геометрической
прогрессии
e
bT1
bT1
- декремент затухания
- логарифмический декремент затухания
Декремент затухания показывает, во сколько раз
уменьшается амплитуда колебаний за один период
6
Затухающие колебания

7. СЛУЧАЙ СИЛЬНОГО СОПРОТИВЛЕНИЯ

k c/m
b / 2m
2
x 2bx k x 0
2
b k
Общее решение уравнения
x C1e
q1t
C2 e
q2 t
q1 b b k , q2 b b k
q1 0 q2 0
2
2
2
2
- апериодическое движение точки, не является типично
колебательным, соответствует достаточно быстрому
затуханию по времени
7
Затухающие колебания

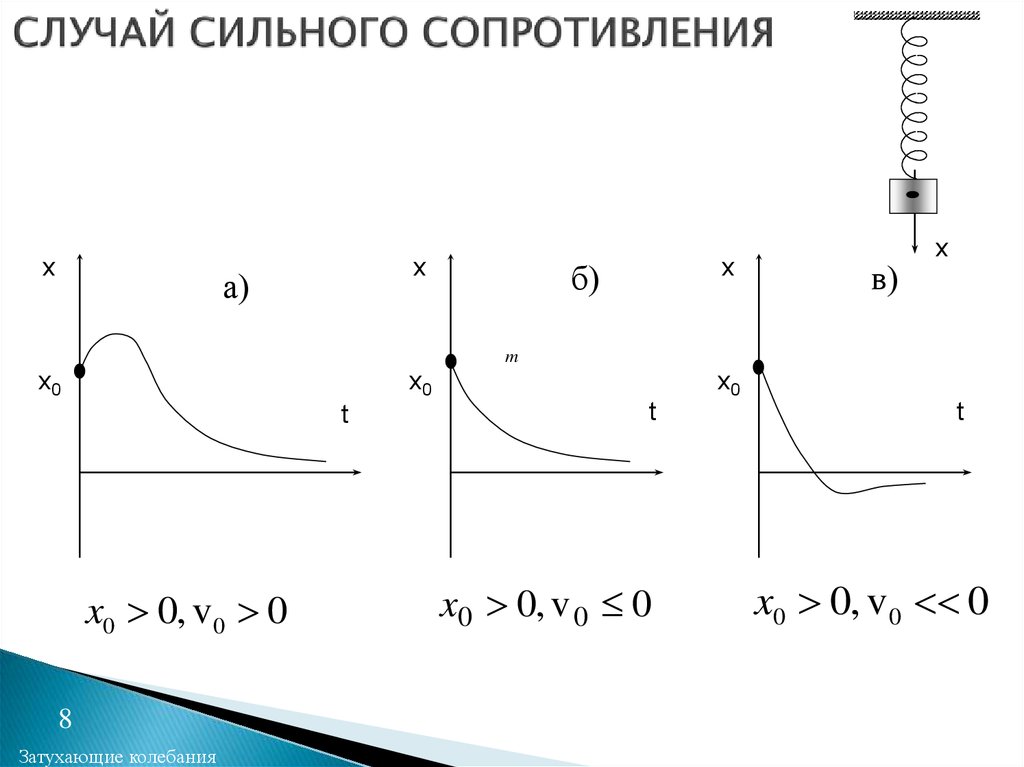
8. СЛУЧАЙ СИЛЬНОГО СОПРОТИВЛЕНИЯ

x
x
а)
x
б)
в)
x
m
x0
x0
t
x0 0, v0 0
8
Затухающие колебания
x0
t
x0 0, v 0 0
t
x0 0, v0 0

9. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ (без учета сопротивления среды)

Q Q0 sin pt - вынуждающая сила
p - частота
Q0 - амплитуда,
Уравнение движения
m x cx Q0 sin pt
Q0
c
x x
sin pt
m
m
ДУ вынужденных колебаний (без учета
сопротивления)
x k x p0 sin pt
2
9
Вынужденные колебания
p0 Q0 / m

10. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

x k x p0 sin pt
2
Это неоднородное уравнение и его решение можно записать
x x1 x2
x1
-общее решение однородного уравнения
(с нулевой правой частью)
x1 A sin( kt )
x2
- частное решение полного уравнения
x2 B sin pt
Подставляя частное решение в ДУ, получим
p 2 B sin pt k 2 B sin pt p0 sin pt
10
Вынужденные колебания

11. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

p B sin pt k B sin pt p0 sin pt
2
2
Это равенство должно выполнятся для любого t
B p0 /( k p )
B(k p ) p0
2
Для случая
2
2
2
p k
x 2 ( p 0 /( k p )) sin pt
2
2
Общее решение
x A sin( kt ) ( p0 /( k p )) sin pt
2
11
Вынужденные колебания
2

12. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

Явление резонанса наступает когда собственная частота
колебаний совпадает с частотой возмущающей силы.
k p
Подставим частное решение полного уравнения
x2 Ct cos pt
в уравнение
x k x p0 sin pt
2
x2 ( p0 / 2 p)t cos pt
или
x2 ( p0 / 2 p)t sin( pt / 2)
- сдвиг по фазе между вынужденными колебаниями и
возмущающей силой равен / 2
- максимальному значению возмущающей силы соответствует
положение статического равновесия и наоборот
12
Вынужденные колебания

13. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

x
p k
x p0t / 2 p
t
x k 2 x p0 sin pt
x p0t / 2 p
Общее решение
x A sin( kt ) ( p0 / 2 p)t cos pt
При резонансе происходит линейный по времени
неограниченный рост амплитуды.
13
Вынужденные колебания