Числа Фибоначчи

1.

ЧИСЛА ФИБОНАЧЧИ
Выполнил учащийся 11-1 класса Вакуленко Данила.
МАОУ Лицея .
Научный руководитель:О.А.Полковский
Г. Калининград, 2019г.

2.

Актуальность
«Числа управляют миром! Число – это сила, царящая
над богами и смертными!» - так говорили ещё
древние пифагорейцы. Изучая в школе науку чисел,
нам хочется убедиться в том, что действительно, явления
всей Вселенной подчинены определенным числовым
соотношениям, найти эту невидимую связь между
математикой и жизнью!

3.

Цель
Изучить проявление чисел Фибоначчи и
связанного с ним закона золотого
сечения в строении живых и неживых
объектов, найти примеры
использования чисел Фибоначчи.

4.

Задачи
Описать способ построения ряда Фибоначчи и спирали
Фибоначчи.
Увидеть математические закономерности, в строении
человека, растительного мира и неживой природы с точки
зрения феномена Золотого сечения.

5.

Кто такой Фибоначчи?
Леонардо Пизанский — первый
крупный математик средневековой Европы.
Наиболее известен под
прозвищем Фибоначчи. Фибоначчи
родился в итальянском городе Пиза,
предположительно в 1170-е годы. Его отец
был торговцем. В 1192 году представлял
пизанскую торговую колонию в Северной
Африке и часто бывал в Алжире. По
желанию отца, Леонардо переехал в Алжир
и изучал там математику у арабских
учителей. Позже Фибоначчи посетил
Египет, Сирию, Византию, Сицилию.

6.

Великое достижение
Удивительные числа были
открыты итальянским
математиком средневековья
Леонардо Фибоначчи.
Путешествуя по Востоку, он
познакомился с
достижениями арабской
математики, способствовал
передаче их на Запад. В
одном из своих трудов он
представил Европе одно из
величайших открытий всех
времён и народов –
десятичную систему
счисления.

7.

Числа, образующие данную
последовательность
называются "числами
Фибоначчи", а сама
последовательность
последовательностью
Фибоначчи. Действительно,
когда появился ряд
Фибоначчи, никто, в том
числе и он сам, не подозревал,
насколько близко ему удалось
приблизиться к разгадке
одной из величайших тайн
мироздания!

8.

Божественная пропорция
В числах Фибоначчи существует интересная
особенность: частное от деления последующего числа
Фибоначчи на предыдущее, по мере роста самих чисел,
стремится к 1,618. Именно это постоянное число
деления в средние века было названо Божественной
пропорцией, а ныне именуется как золотое сечение или
золотая пропорция.
В алгебpе это число обозначается гpеческой буквой фи
(Ф)
Итак, φ = 1,618
233 / 144 = 1,618
377 / 233 = 1,618
610 / 377 = 1,618
987 / 610 = 1,618
1597 / 987 = 1,618
2584 / 1597 = 1,618

9.

Обратная пропорция
При делении меньшего числа на последующее
большее получаем частное 0, 618, это число,
обратное к 1, 618, тоже называется золотой
пропорцией.

10.

Что такое спираль Фибоначчи?
В математике нет иной формы, которая обладала бы
такими же уникальными свойствами, как спираль,
потому, в основе строения спирали лежит правило
Золотого сечения ! Золотое сечение - это такое
пропорциональное деление отрезка на неравные части,
при котором весь отрезок так относится к большей
части, как сама большая часть относится к меньшей.

11.

Удивительные свойства числового
ряда
Учёные, анализируя дальнейшее
применение этого числового ряда к
природным феноменам и процессам,
обнаружили, что эти числа содержатся
буквально во всех объектах живой
природы, в растениях, в животных и в
человеке. Удивительная математическая
игрушка оказалась уникальным кодом,
заложенным во все природные объекты
Вселенной. Рассмотрим примеры, где
встречаются числа Фибоначчи в живой и
неживой природе.

12.

Золотое сечение в природе
Подсолнечник: 21 и 34 спирали.
Эхинацея, 34 и 55 спиралей.

13.

Чёткая, симметричная форма цветов также подчинена
строгому закону. У многих цветов количество
лепесточков – именно числа из ряда Фибоначчи.
Например:
ирис, 3 лепестка
астра, 34 лепестка
лютик, 5 лепестков
дельфиниум, 13 лепестков
маргаритки,55 лепестков

14.

В форме спирали развиваются рога и бивни
животных, когти львов и клювы попугаев являют
собой логарифмические формы и напоминают форму
оси, склонной обратиться в спираль.
Попугай и его клюв
Горный козел и его рога
спиралевидной формы

15.

Золотое сечение в природных
явлениях
Интересно, что спиралью закручивается ураган,
облака циклона и антициклона и это хорошо
видно из космоса:

16.

В океанских и морских волнах спираль можно
математически отразить на графике с точками
1,1,2,3,5,8,13,21,34 и 55
вода убегает из ванной по
спирали:
Мы живём в спирали, ведь галактика –
это спираль, соответствующая
формуле Золотого сечения.

17.

Золотое сечение в анатомии
человека
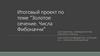
Достаточно лишь
приблизить сейчас вашу
ладонь к себе и внимательно
посмотреть на указательный
палец, и вы сразу же найдете
в нем формулу золотого
сечения. Каждый палец
нашей руки состоит из трех
фаланг.
Сумма двух первых фаланг
пальца в соотношении со
всей длиной пальца и дает
число золотого сечения.

18.

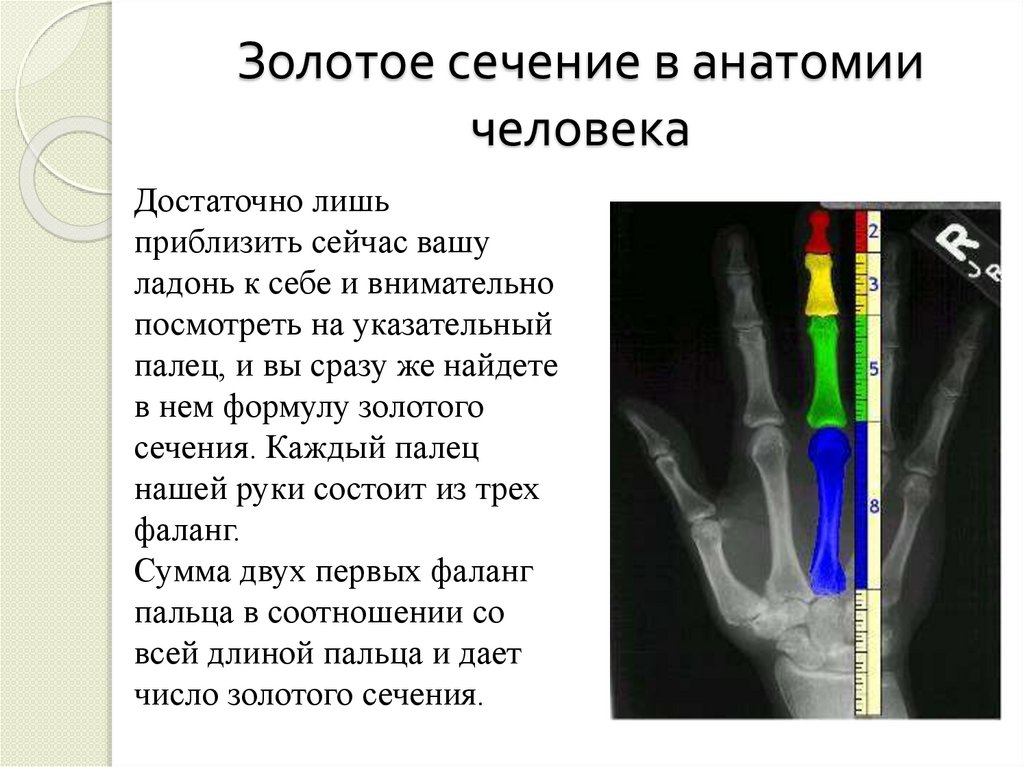
В строении легких человека также
существует золотое сечение.
Особенность бронхов заключена в
их асимметричности. Бронхи состоят
из двух основных дыхательных
путей, один из которых (левый)
длиннее, а другой (правый) короче.
Было установлено, что эта
асимметричность продолжается во
всех более мелких дыхательных
путях. Причем соотношение длины
коротких и длинных бронхов также
составляет золотое сечение и равно
1:1,618.

19.

Все сведения о физиологических особенностях живых
существ хранятся в микроскопической молекуле ДНК,
строение которой также содержит в себе закон
золотой пропорции. Молекула ДНК состоит из двух
вертикально переплетенных между собой спиралей.

20.

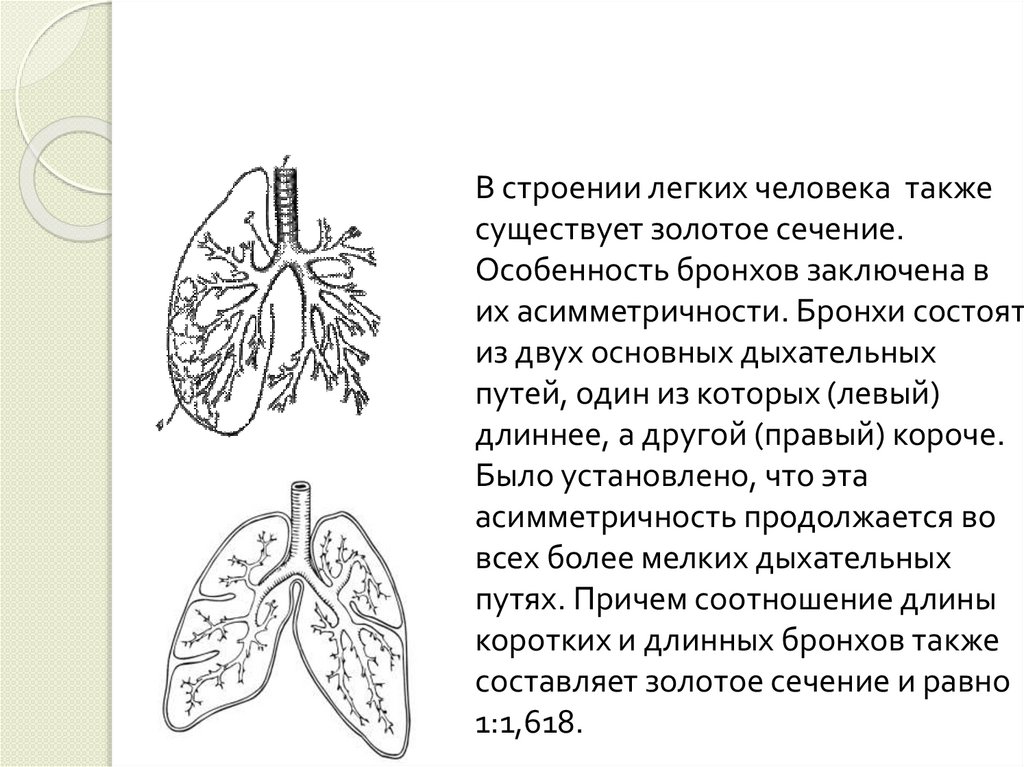
Спирали есть на наших ладошках и пальцах:
Спирали есть и в человеке. С помощью
спиралей мы слышим:

21.

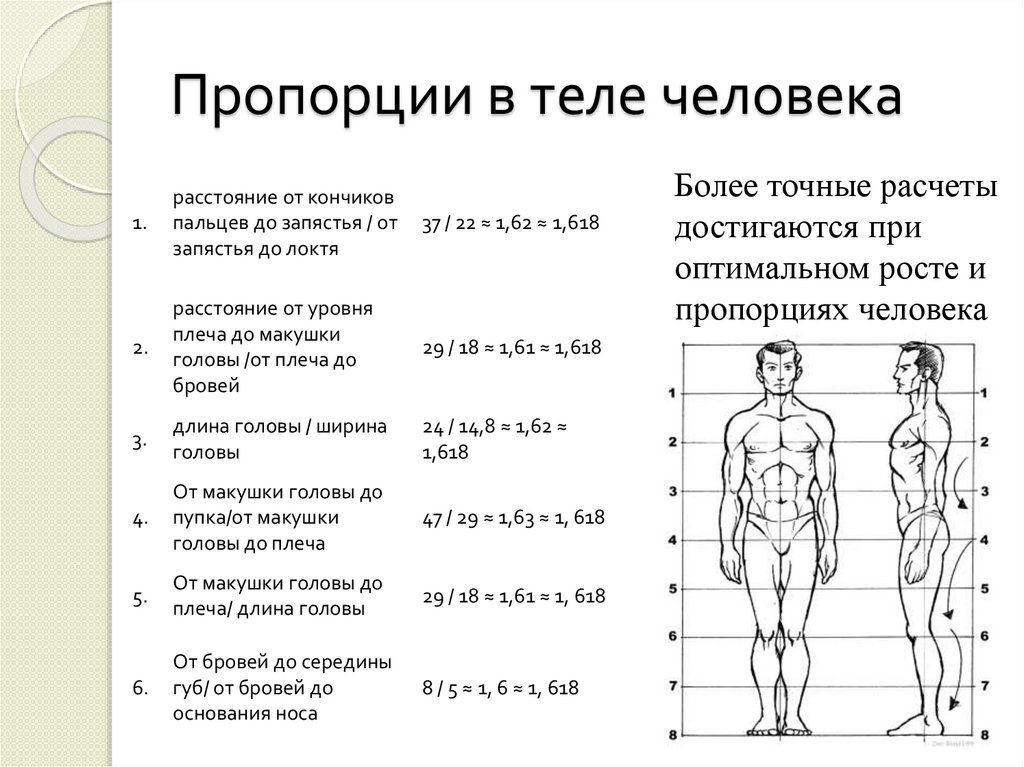
Пропорции в теле человека
1.
расстояние от кончиков
пальцев до запястья / от
запястья до локтя
37 / 22 ≈ 1,62 ≈ 1,618
2.
расстояние от уровня
плеча до макушки
головы /от плеча до
бровей
29 / 18 ≈ 1,61 ≈ 1,618
3.
длина головы / ширина
головы
24 / 14,8 ≈ 1,62 ≈
1,618
4.
От макушки головы до
пупка/от макушки
головы до плеча
47 / 29 ≈ 1,63 ≈ 1, 618
5.
От макушки головы до
плеча/ длина головы
29 / 18 ≈ 1,61 ≈ 1, 618
6.
От бровей до середины
губ/ от бровей до
основания носа
8 / 5 ≈ 1, 6 ≈ 1, 618
Более точные расчеты
достигаются при
оптимальном росте и
пропорциях человека

22.

Золотое сечение в архитектуре
В архитектуре Древнего
Египта по правилам золотой
пропорции была построена
пирамида Хеопса. Здесь
можно увидеть треугольник с
прямым углом, один катет
которого является высотой,
второй – половиной длины
основания. Если взять
отношение гипотенузы к
меньшей стороне, получим
идеальное значение 1,61950.

23.

Идеальные пропорции в древней
Греции
Парфенон, который возведен в 5 веке до нашей эры.
Если взять отношение его высоты к ширине,
получится практически идеальное число 0,618.
Ученые определили, что для абсолютного золотого
числа нужно отнять от высоты 14 см и прибавить
их к ширине. Учитывая строение сооружения,
очень похоже, что это было сделано намеренно,
поскольку фасад немного сужается в верхней части
и отклоняется от золотого прямоугольника. Но
общие пропорции золотого сечения соблюдены.

24.

25.

Прекрасным памятником
истории архитектуры
средневековья, сохранившимся
до нашего времени, является
собор Парижской Богоматери
или Нотр-Дам де Пари.

26.

Дом Советов был возведен по проекту
Троцкого в 1941 году. По обе стороны
расположены два корпуса высотой в 5 этажей.
Длина здания – 1472 единицы, если разделить
его на значение Ф = 1,618, получим размерный
ряд: 1472, 909, 562, 347, 214, 132, 81, 50. К ним
относятся высота входа, всего сооружения,
различных элементов.

27.

Золотое сечение в искусстве
Великий Леонардо да Винчи является едва ли не
самым известным поклонником «золотого принципа»
в живописи. Композиция многих его картин построена
именно на основе «Божественной пропорции»

28.

Именно Леонардо да Винчи наглядно продемонстрировал
связь золотого сечения и пропорций тела. Сделал он это в
своем чернильном рисунке «Витрувианский человек», где
была отражена гармония и соразмерность частей тела
относительно друг друга.
Фреска «Тайная вечеря» Леонардо да Винчи

29.

Известные картины на религиозную тематику во многом
обязаны золотой пропорции величественным и
умиротворяющим впечатлением, которое производят.
«Святое семейство» Микеланджело
«Сикстинская Мадонна» Рафаэля

30.

Вывод
В наших исследованиях мы увидели, что
в окружающих нас растениях,
живых организмах и даже в
строении человека проявляют себя числа из
последовательности Фибоначчи, что
отражает гармоничность их строения.
Сосновая шишка, тысячелистник,
комар, человек устроены с
математической точностью.​

31.

Использованная литература
1.http://www.chydesasveta.ru/en/chisla_fibonachchi.html​
2.http://zagadkamozga.ru/node/630​
3.http://magov.net/blog/3621.html​
4.http://greenword.ru/2009/06/fibonaccisequence.html​
5.http://esopedia.ru/ChislaFibonachchi

32.

Спасибо за внимание!