Комбинаторика и её формулы

1.

Комбинаторика и
её формулы
Щепетев Никита Константинович СА-12

2.

Комбинаторика – раздел математики, изучающий дискретные
объекты, множества (сочетания, перестановки, размещения и
перечисления элементов) и отношения на них (например,
частичного порядка).
Говоря простым языком, комбинаторика изучает задачи, основным
вопросом которых является «Сколькими способами/вариантами/…»
Одним из важнейших понятий современной математики является понятие множества.
Говорят о множестве учащихся в группе, о множестве букв в алфавите, о множестве
изделий в упаковке и т.д.
Понятие множества относится к первоначальным, простейшим, понятиям и формально
через другие более простые понятия не определяется. Оно воспринимается конкретно,
посредством знакомства с различными примерами множества. Множество
характеризуется объединением некоторых однородных объектов в одно целое. Объекты,
образующие множество, называются элементами множества.
Множества элементов называются соединениями.

3.

Для формулировки и решения комбинаторных задач используют различные
модели комбинаторных конфигураций. Примерами комбинаторных
конфигураций являются:
Размещением из n элементов по k называется упорядоченный набор из k различных
элементов некоторого n-элементного множеств.
Перестановкой из n элементов (например чисел 1, 2, … n) называется всякий упорядоченный
набор из этих элементов. Перестановка также является размещением из n элементов по n.
Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов.
Наборы, отличающиеся только порядком следования элементов (но не составом), считаются
одинаковыми, этим сочетания отличаются от размещений.

4.

Определения:
В комбинаторике размеще
́ нием (из n по k) называется упорядоченный
набор из k различных элементов из некоторого множества различных n
элементов.
Перестано
́ вка в комбинаторике — упорядоченный набор без повторений чисел
(1.2.3.4…n) обычно трактуемый как биекция на множестве {1.2.3.4…n}, которая числу
ставит в соответствие i-й элемент из набора. Число n при этом называется длиной
перестановки
В комбинаторике сочетанием из n по k называется набор из k элементов, выбранных
из n -элементного множества, в котором не учитывается порядок элементов.

5.

Формулы этих способов:
Перестановки:
Pn = n·(n−1)·(n−2)...3·2·1 = n!
Размещения:
Anm = n·(n − 1)·(n − 2)·...·(n − m + 1) = n!/(n − m)!
Сочетания:
Сnm = n!/(n − m)!/m!

6.

Задачи:
Задача 1.
На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом 1-й и 2-й тома не стояли рядом?
Задача 2.
На книжной полке стояло 30 томов. Ребенок уронил книги с полки, а затем расставил их в случайном порядке. Какова вероятность того, что он не
поставил 1-й и 2-й тома рядом?
Задача 3.
Сколькими способами можно расставить 15 томов на книжной полке, если выбирать их из имеющихся в наличии 30-ти книг?
Задача 4.
Сколькими способами можно расставить 30 книг на двух полках, если на каждой из них помещается только по 15 томов?
Задача 5.
Сколькими способами можно расставить 15 томов на книжной полке, если выбирать их из имеющихся в наличии внешне
неразличимых 30-ти книг?
Задача 6.
Сколькими способами можно расставить 30 внешне неразличимых книг на двух полках, если на каждой из них помещается
только по 15 томов?

7.

Бином Ньютона.
К примеру, известная формула сокращенного умножения "квадрат
суммы" вида есть частный случай бинома Ньютона при n=2.
Выражение, которое находится в правой части формулы бинома
Ньютона, называют разложением выражения (a+b)n, а выражение
называют (k+1)-ым членом разложения, k=0,1,2,…,n.

8.

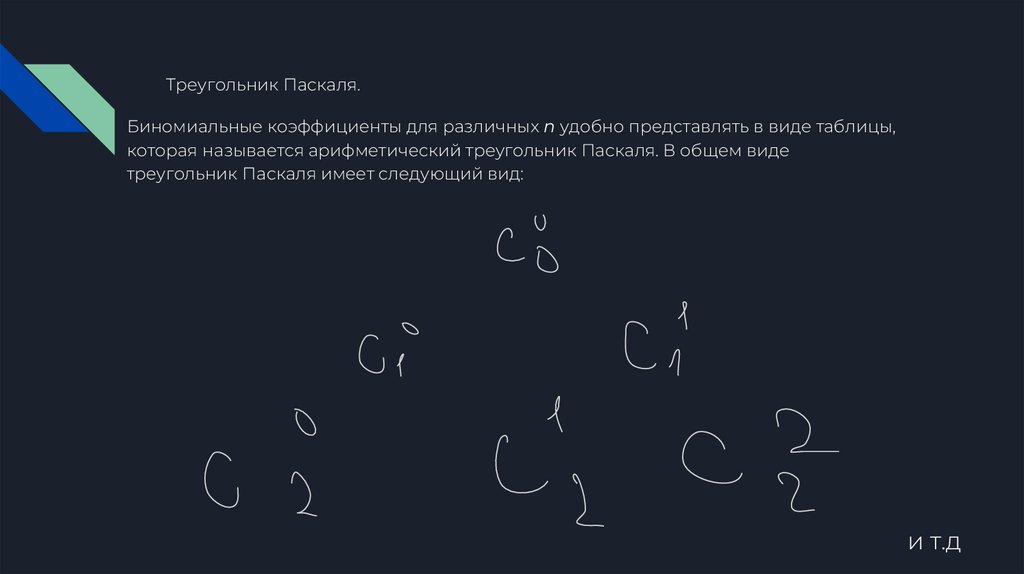
Треугольник Паскаля.
Биномиальные коэффициенты для различных n удобно представлять в виде таблицы,
которая называется арифметический треугольник Паскаля. В общем виде
треугольник Паскаля имеет следующий вид:
и т.д

9.

Спасибо за внимание!