Похожие презентации:
Интеллектуальные системы и технологии
1. Интеллектуальные системы и технологии
2. История развития искусственного интеллекта
3. История развития искусственного интеллекта за рубежом
1.2.
3.
4.
1235-1315 – Р.Луллий
XVIII - Г.Лейбниц и Р. Декарт
(независимо друг от друга)
40 –х года XX века – Н.Винер
1956 г. – предложен термин
искусственный интеллект
4. Искусственный интеллект – как самостоятельная отрасль
НейрокибернетикаЕдинственный объект,
способный мыслить – это
человеческий мозг
нейронные сети
(нейросети)
Кибернетика
«черного ящика»
Не имеет значение, как
устроено «мыслящее»
устройство. Главное
чтобы на заданные
входные воздействия
оно реагировало так
же, как человеческий
мозг
алгоритмы и модели
человеческого
мышления
5.
История развитиянейронных сетей
1.
2.
3.
конец 50-х Г.Розенблатт,П.МакКаллок (перцептрон)
70-80 года –
исследования
снижались
середина 80 годов –
создание
нейрокомпьютера
(транспьютеры)
Подходы
1.
2.
3.
4.
Конец 50-х – модель
лабиринтного поиска
Начало 60-х –
эвристическое
программирование
1963-1970 – методы
математической
логики
Середина 70-х –
экспертные системы
6. Подходы к созданию нейросетей
1.2.
3.
Аппаратный
Программный
Гибридный
7. История развития искусственного интеллекта в России
1.2.
3.
4.
5.
1954 год- семинар «Автоматы и
мышление»
1945-1964 г.г- программы и исследуются
поиск решения логических задач
1965-1980 г.г. – ситуационное управление
1980-1990 г.г. – исследования в области
представления знаний
1988 г. – ассоциация искусственного
интеллекта
8. Основные направления исследований в области ИИ
Искусственный интеллект – одно изнаправлений информатики, цель которого
разработка аппаратно-программных
средств, позволяющих пользователюнепрограммисту ставить и решать свои
задачи, традиционно считающиеся
интеллектуальными, общаясь с ЭВМ на
ограниченном подмножестве естественного
языка.
9. Классификация направлений
1.2.
3.
4.
5.
Разработка интеллектуальных
информационных систем или
систем, основанных на знаниях
Разработка естественно-языковых
интерфейсов и машинный перевод
Генерация и распознавание речи
Обработка визуальной информации
Обучение и самообучение
10. Классификация ИИС
Характерные признаки (интеллектуальныесвойства)
развитые коммуникативные способности
умение решать сложные плохо
формализуемые задачи
способность к самообучению
адаптивность
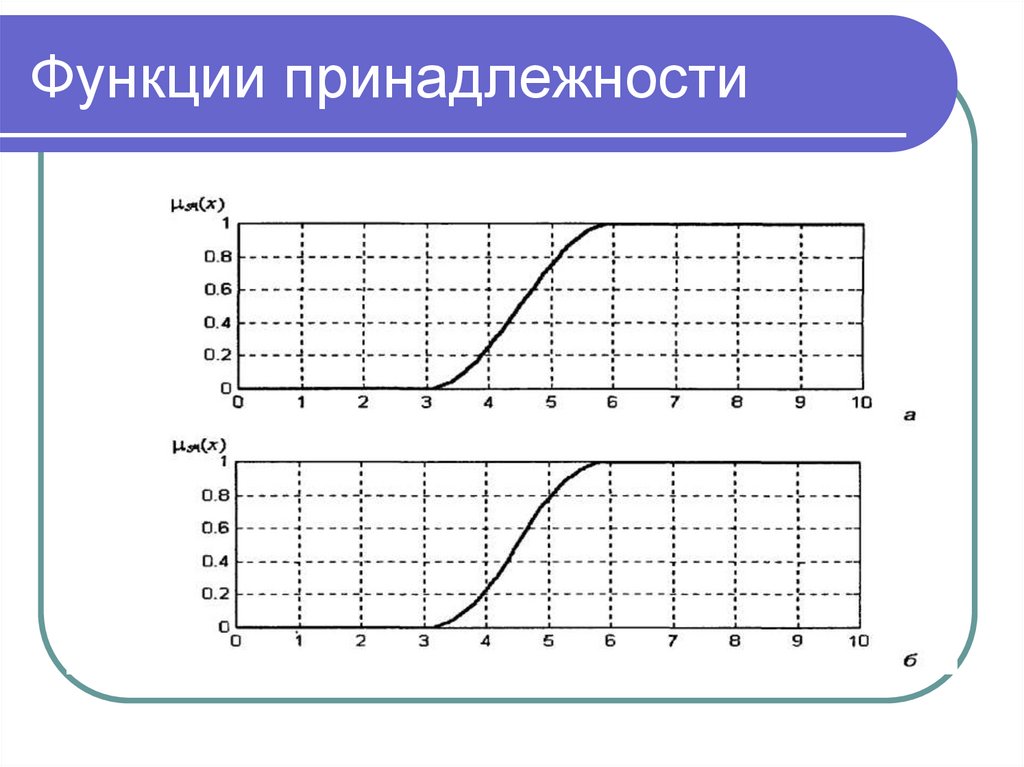
11. Нечеткое множество
Нечетким множеством (fuzzy set) А науниверсальном множестве X называется
совокупность пар ( А(X),x), где А(X) - степень
принадлежности элемента u U к нечеткому
множеству А. Степень принадлежности - это число
из диапазона [0,1]. Чем выше степень
принадлежности, тем в большей мерой элемент
универсального множества соответствует
свойствам нечеткого множества.
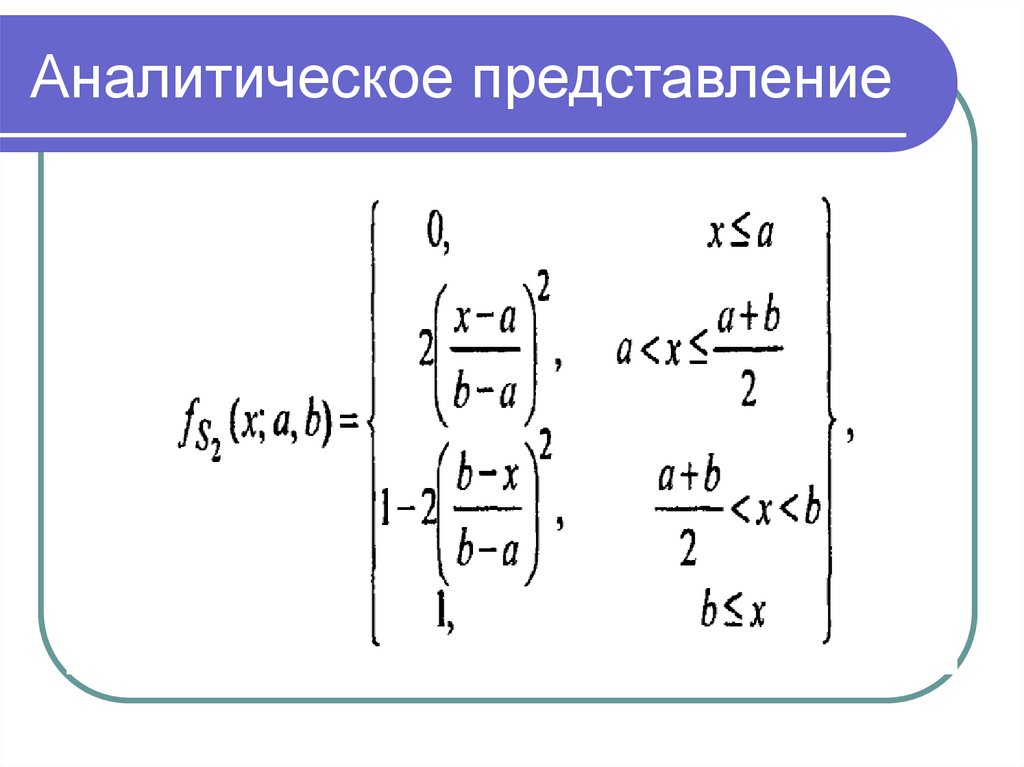
• Функцией принадлежности (membership function)
называется функция, которая позволяет вычислить
степень принадлежности произвольного элемента
универсального множества к нечеткому множеству.
12.
Если универсальное множество состоит изконечного количества элементов
X=(x1,x2,…,xn) , тогда нечеткое множество
записывается в виде:
В случае непрерывного множества U
используют следующее обозначение:
Пример: Представить в виде нечеткого множества
понятие “мужчина среднего роста”.
Решение: 0/155+0.1/160 + 0.3/165 + 0.8/170 +1/175
+1/180 + 0.5/185 +0/190.
13.
Примеры записей нечеткогомножества:
X={x1, x2, x3, x4, x5}
Пусть А-нечеткое множество для
которого
µ(x1)=3, µ(x2)=0 µ(x3)=1
µ(x4)=0,5 µ(x5)=0,9
Тогда А можно представить в виде
А=0,3/х1+0/x2+1/х3+0,5/х4+0,9/х5,
где здесь знак + есть знак объединения.
Или А={0,3/х1 ;0/x2 ;1/х3 ;0,5/х4 ;0,9/х5}
14.
Пусть X={0,1,2,…n….};Нечеткое множество “малый” можно
определить с помощью формулы
следующем образом
«малый»(n)=1/(1+(n/10)2)
15.
Е = { Иванов, Петров, Сидоров, …}задается
с
помощью
функции
принадлежности
µ«молодой»(x)
на
множестве
X= {1, 2, 3, … 100} (возраст),
16.
Пусть Е={Запорожец, Жигули ,Мерседес, Феррари…..};
X=[0, ]- универсальное множество
(стоимость). Тогда на E мы можем
определить нечеткие множество типа
“ для бедных”; ” для среднего класса”;
“престижные”
17. Свойства нечетких множеств
Высота нечеткого множестваВысотой нечеткого множества называется
верхняя граница его функции
принадлежности:
Для дискретного универсального множества
супремум становится максимумом, а значит
высотой нечеткого множества будет максимум
степеней принадлежности его элементов
18. Нормальное нечеткое множество
Нечеткое множество называетсянормальным, если его высота равна
единице. Нечеткие множества не
являющиеся нормальными называются
субнормальными.
Нормализация - преобразование
субнормального нечеткого множества в
нормальное определяется так:
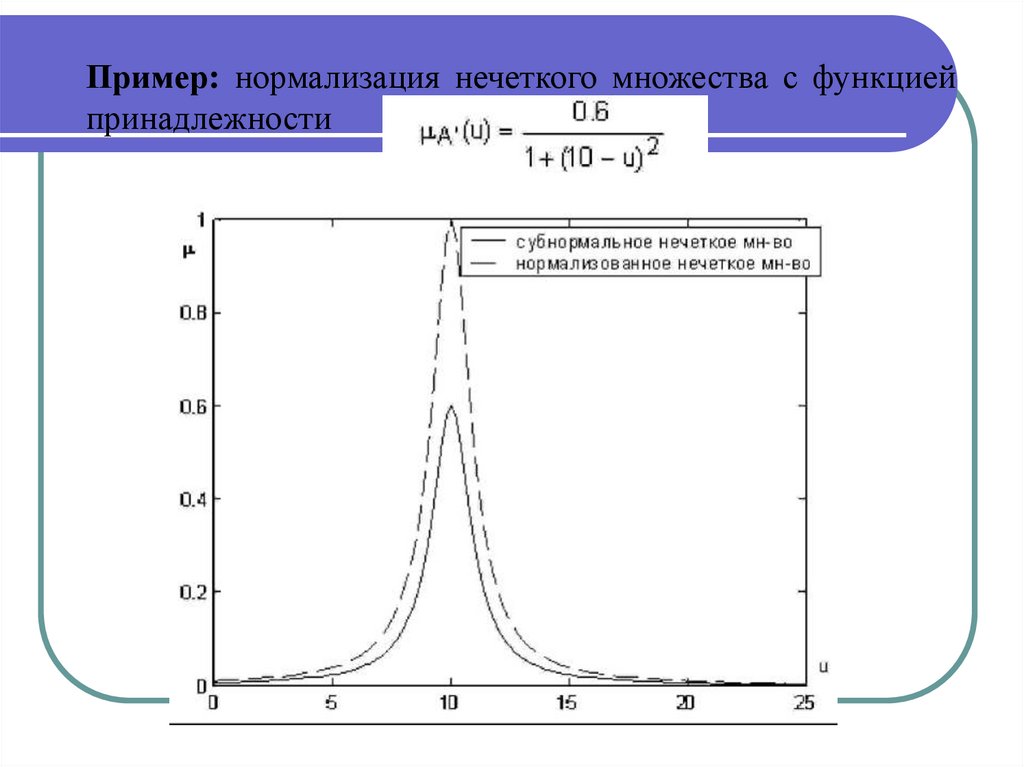
19.
Пример: нормализация нечеткого множества с функциейпринадлежности
20. Носитель нечеткого множества
Носителемнечеткого
множества
называется
четкое
подмножество
универсального множества U, элементы
которого
имеют
ненулевые
степени
принадлежности:
Пустое нечеткое множество
Нечеткое множество называется пустым, если
его носитель является пустым множеством.
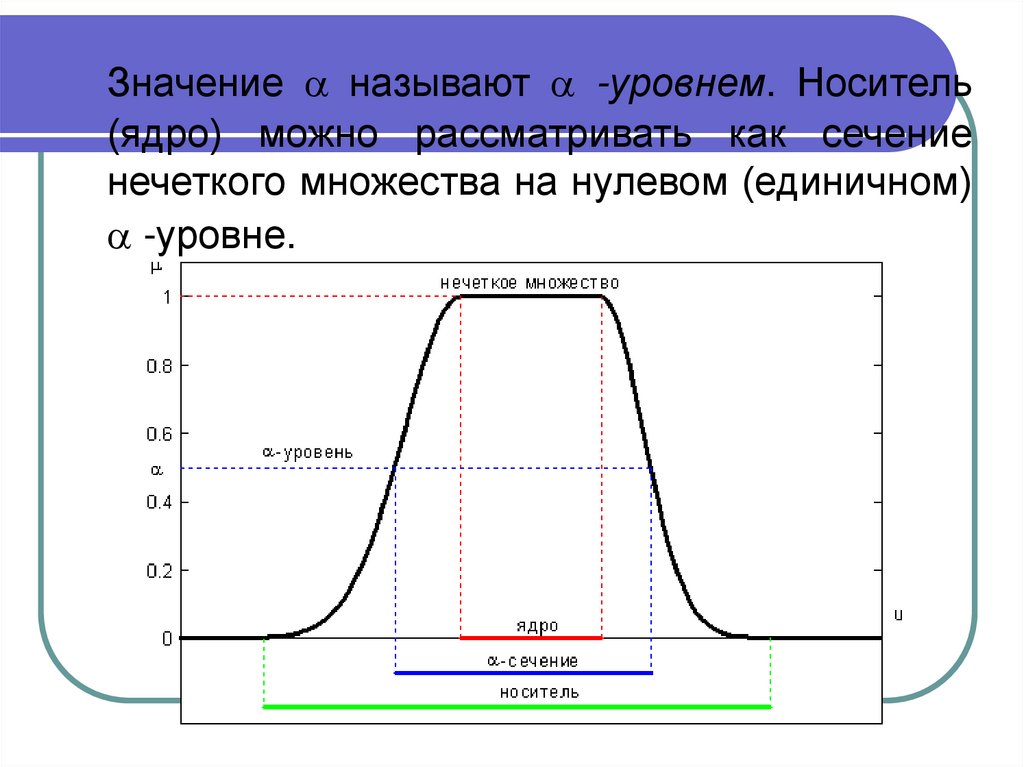
21. Ядро нечеткого множества
Ядром нечеткого множества называется четкоеподмножество универсального множества U,
элементы
которого
имеют
степени
принадлежности равные единице:
-сечением (или множеством -уровня) нечеткого
множества
называется
четкое
подмножество
универсального множества u, элементы которого
имеют степени принадлежности большие или
равные :
22.
Значение называют -уровнем. Носитель(ядро) можно рассматривать как сечение
нечеткого множества на нулевом (единичном)
-уровне.
23.
Равенство нечетких множествНечеткие множества А и В равны если
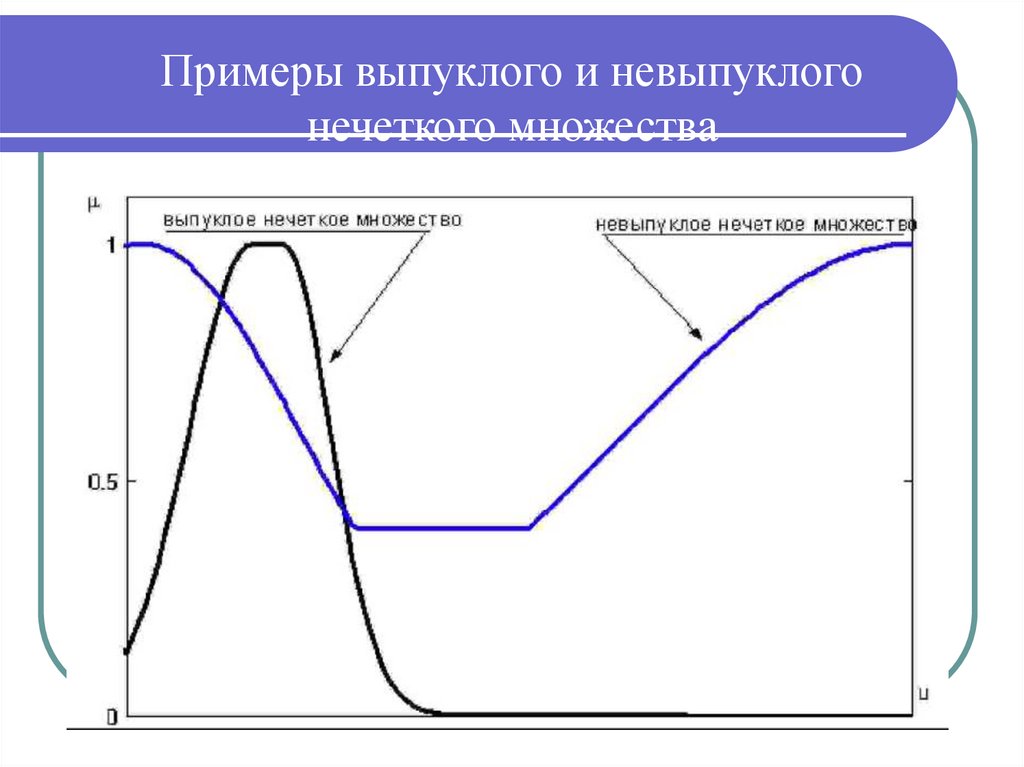
Нечеткое множество называется выпуклым
если:
нечеткое множество будет выпуклым, если все его
-сечения - выпуклые множества.
24.
Примеры выпуклого и невыпуклогонечеткого множества
25.
Операции над НМ в максминном базисе1. Пересечение: A B- наибольшее
нечеткое подмножество, содержащееся
одновременно в A и B
а b(x)= min ( a(x), b(x))
2. Объединение: A B- наименьшее
нечеткое подмножество, включающее,
как
A так
и
B
с
функцией
принадлежности
а b(x)= max ( a(x), b(x))
Разность
A-B=A∩(не В): µa-b(x)=min(µa(x),1-µb(x))
26.
ПримерыПусть А = 0,4/x1+0,2/x2+0/x3+1/x4
B = 0,7/x1+0,9/x2+0,1/x3+1/x4
Видно, что A B
А≠В
Ā = 0,6/x1 + 0,8/x2+1/x3+0/x4
A B = 0,4/x1+0,2/x2+0/x3+1/x4
A B = 0,7/x1+0,9/x2+0,1/x3+1/x4
A-B = 0,3/x1+0,1/x2+0/x3+0/x4
27.
Дополнением нечётких множеств A и Bназывается множество
функция принадлежности элементов к
которому определяется как
A ( x) 1 A ( x)

























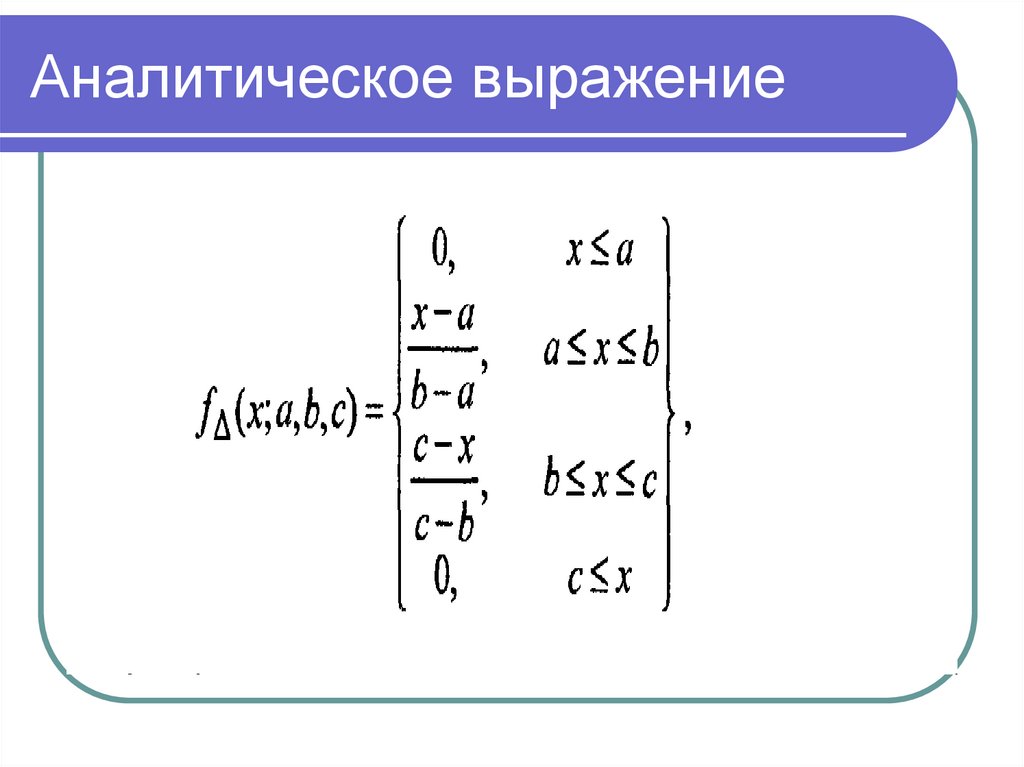
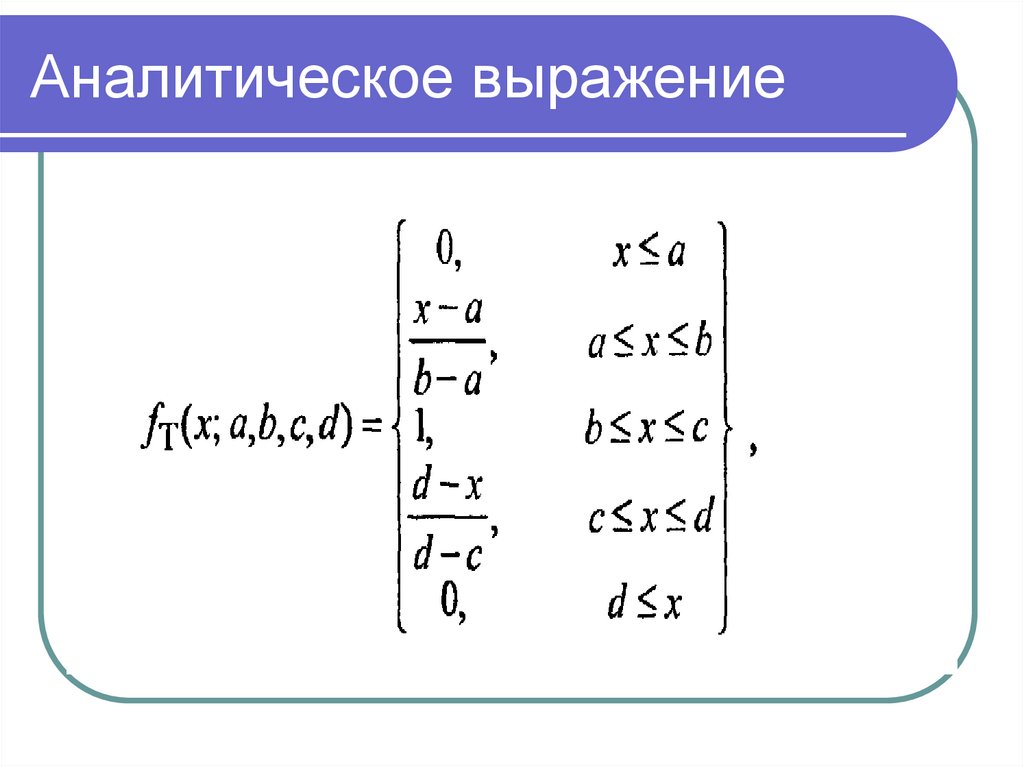
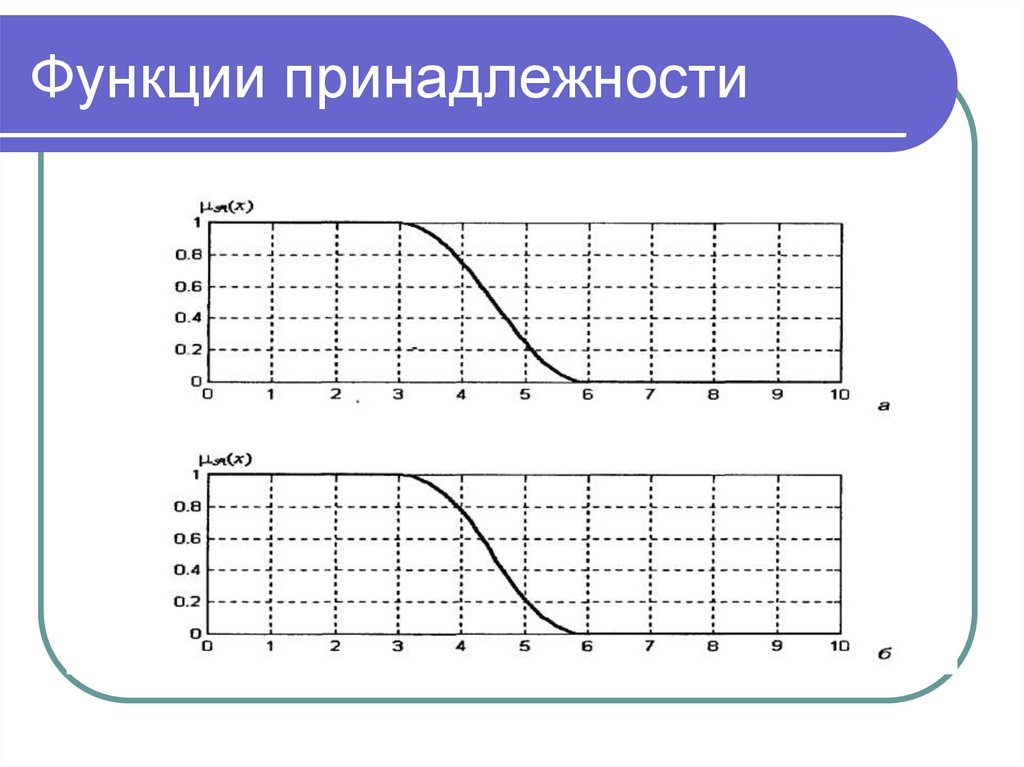

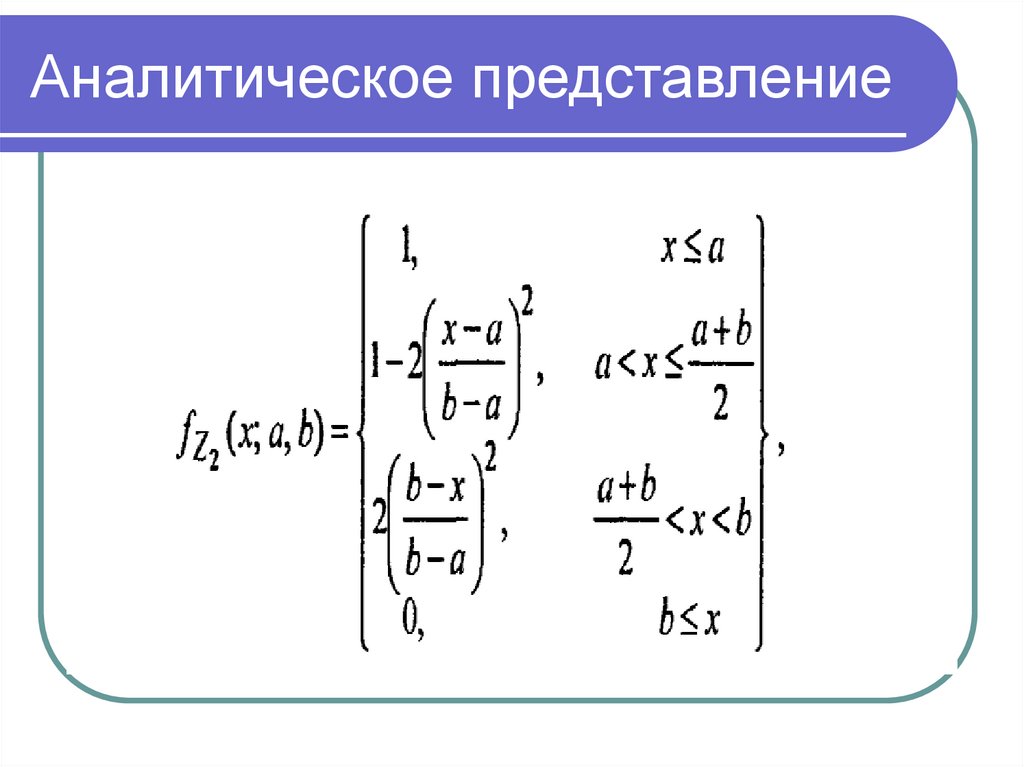


 Математика
Математика








