Похожие презентации:
Элементы теории нечетких множеств
1. Элементы теории нечетких множеств
2. Содержание
ВведениеОсновные определения
Основные операции над нечеткими множествами
Типичные одномерные функции принадлежности
Заключение
Список литературы
3. Введение
Современные интеллектуальные системы базируются на нечеткой логикепри принятии решений и адаптации к изменяющимся условиям среды
Основа нечеткой логики - нечеткие множества и нечеткие правила
В классической теории множеств рассматриваются множества с четкой
границей:
A x x 0
Нечеткое множество:
не имеет четкой границы,
характеризуется функцией принадлежности,
позволяют моделировать часто используемые лингвистические
выражения
Примеры:
Высокий рост
Близко
Погода холодная
Нечеткость множеств проистекает из неопределенной и неточной природы
понятий и выражений естественных языков
4. Основные определения
Пусть X - универсальное множество, содержащее элементы xМножество A задается характеристической функцией A x :
1, x A,
0, x A.
A x
С=«желательный вид транспорта для поездки из Москвы в Санкт-Петербург»
С={(поезд, 0.9), (самолет, 0.6), (автомобиль, 0.4)}
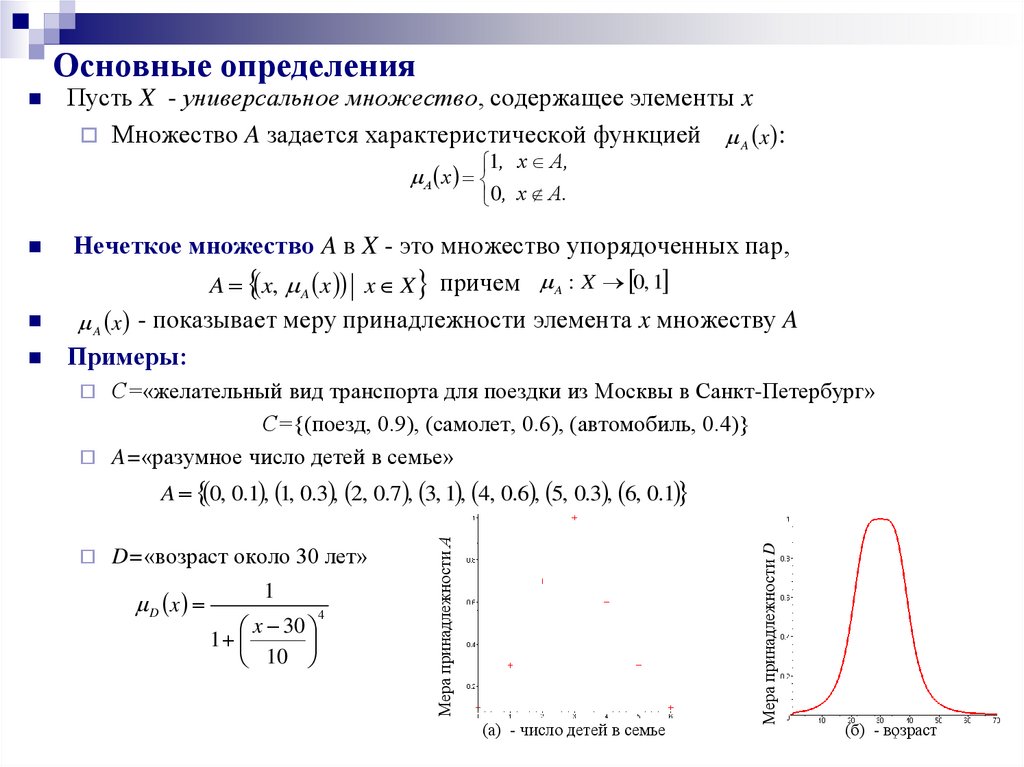
A=«разумное число детей в семье»
A 0, 0.1 , 1, 0.3 , 2, 0.7 , 3, 1 , 4, 0.6 , 5, 0.3 , 6, 0.1
D=«возраст около 30 лет»
D x
1
x 30
1
10
4
(а) - число детей в семье
Мера принадлежности D
Нечеткое множество A в X - это множество упорядоченных пар,
A x, A x x X причем A : X 0, 1
A x - показывает меру принадлежности элемента x множеству A
Примеры:
Мера принадлежности А
(б) - возраст
5.
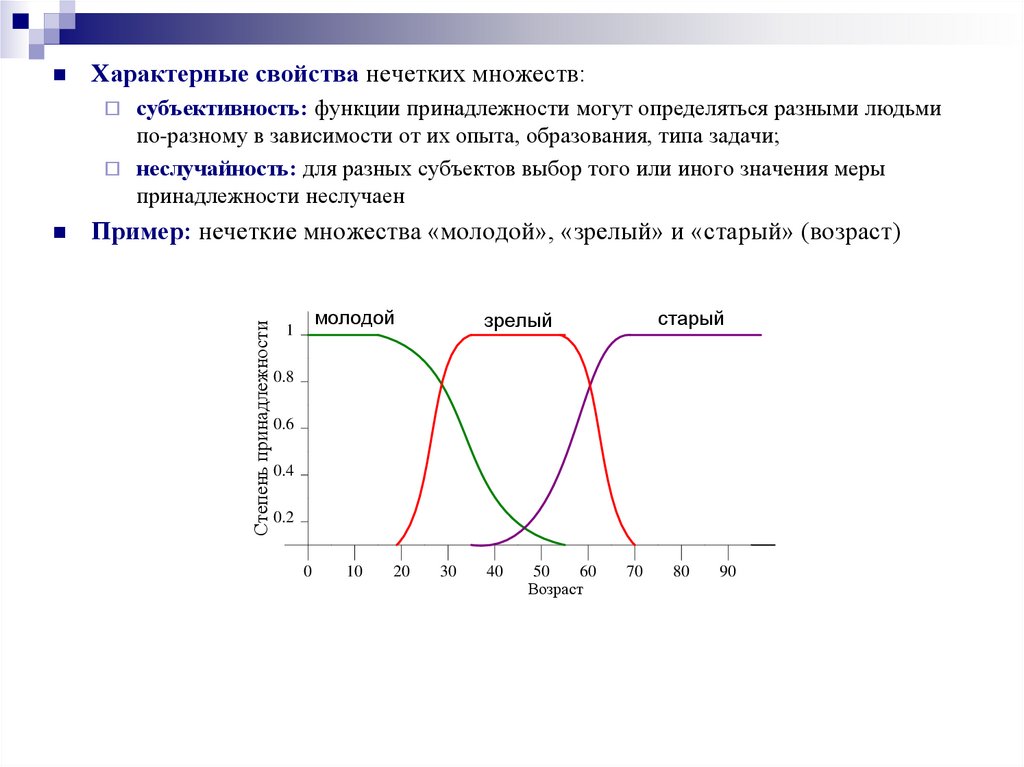
Характерные свойства нечетких множеств:субъективность: функции принадлежности могут определяться разными людьми
по-разному в зависимости от их опыта, образования, типа задачи;
неслучайность: для разных субъектов выбор того или иного значения меры
принадлежности неслучаен
Пример: нечеткие множества «молодой», «зрелый» и «старый» (возраст)
Степень принадлежности
молодой
1
старый
зрелый
0.8
0.6
0.4
0.2
0
10
20
30
40
50
60
Возраст
70
80
90
6.
~~
Степень принадлежности
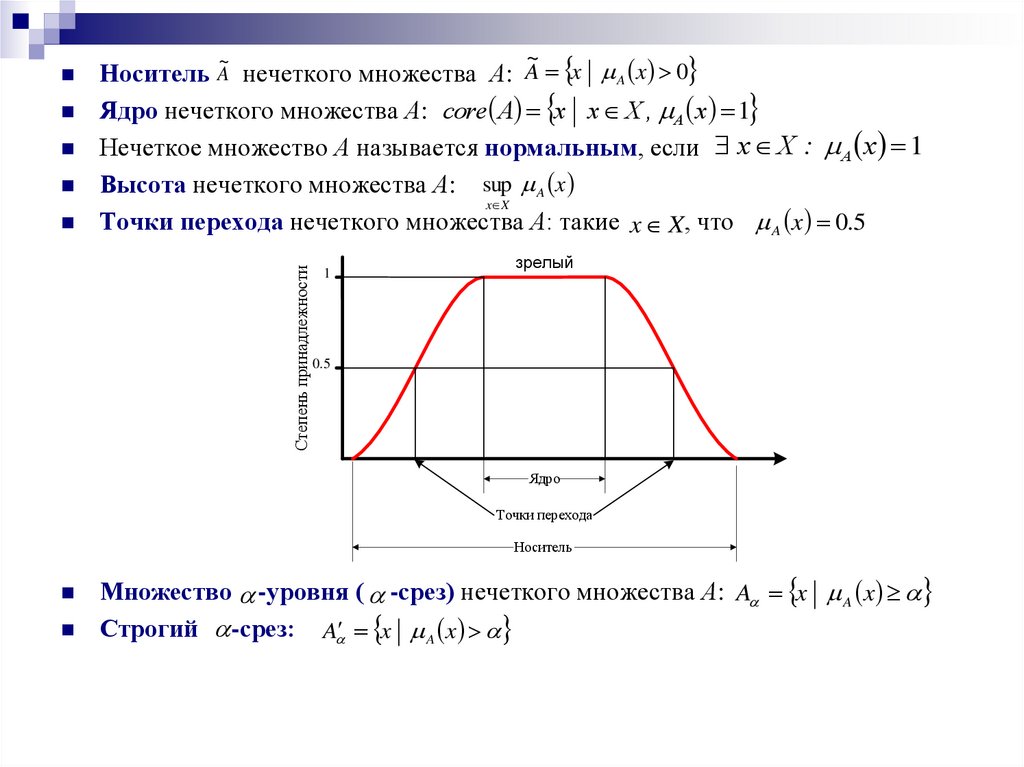
Носитель A нечеткого множества А: A x A x 0
Ядро нечеткого множества А: core A x x X , A x 1
Нечеткое множество А называется нормальным, если x X : A x 1
Высота нечеткого множества А: sup A x
x X
Точки перехода нечеткого множества А: такие x X, что A x 0.5
1
зрелый
0.5
Ядро
Точки перехода
Носитель
Множество -уровня ( -срез) нечеткого множества А: A x A x
Строгий -срез: A x A x
7.
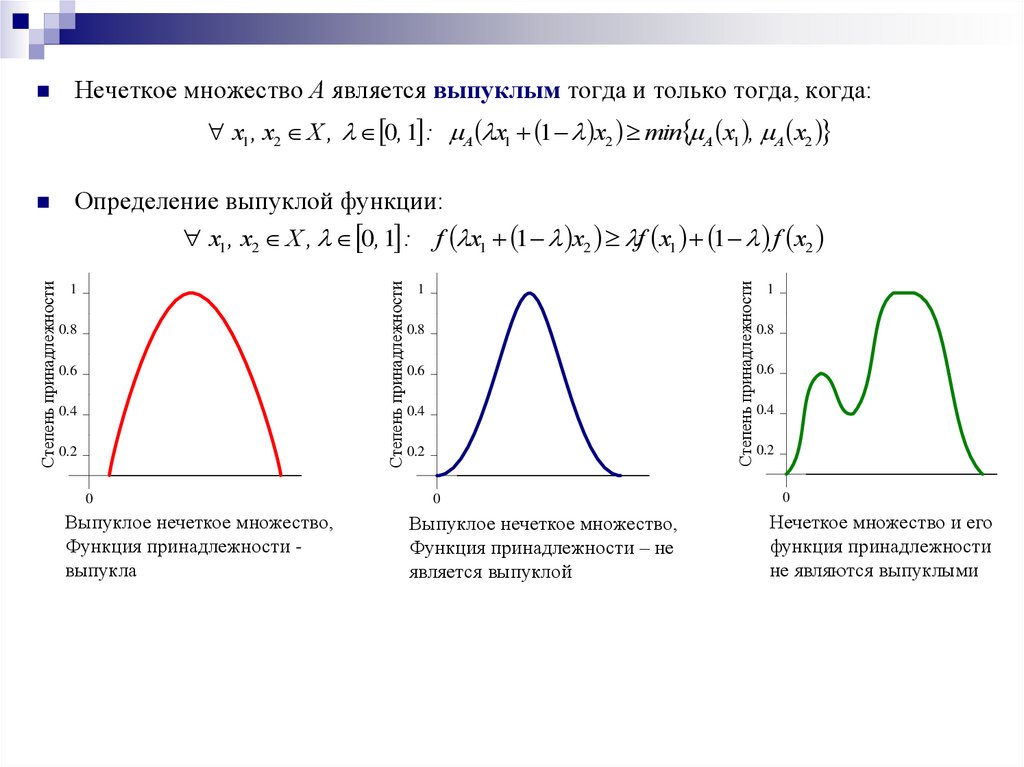
Нечеткое множество А является выпуклым тогда и только тогда, когда:x1 , x2 X , 0, 1 : A x1 1 x2 min A x1 , A x2
1
0.8
0.6
0.4
0.2
0
Выпуклое нечеткое множество,
Функция принадлежности выпукла
Степень принадлежности
Определение выпуклой функции:
x1 , x2 X , 0, 1 : f x1 1 x2 f x1 1 f x2
Степень принадлежности
Степень принадлежности
1
0.8
0.6
0.4
0.2
0
Выпуклое нечеткое множество,
Функция принадлежности – не
является выпуклой
1
0.8
0.6
0.4
0.2
0
Нечеткое множество и его
функция принадлежности
не являются выпуклыми
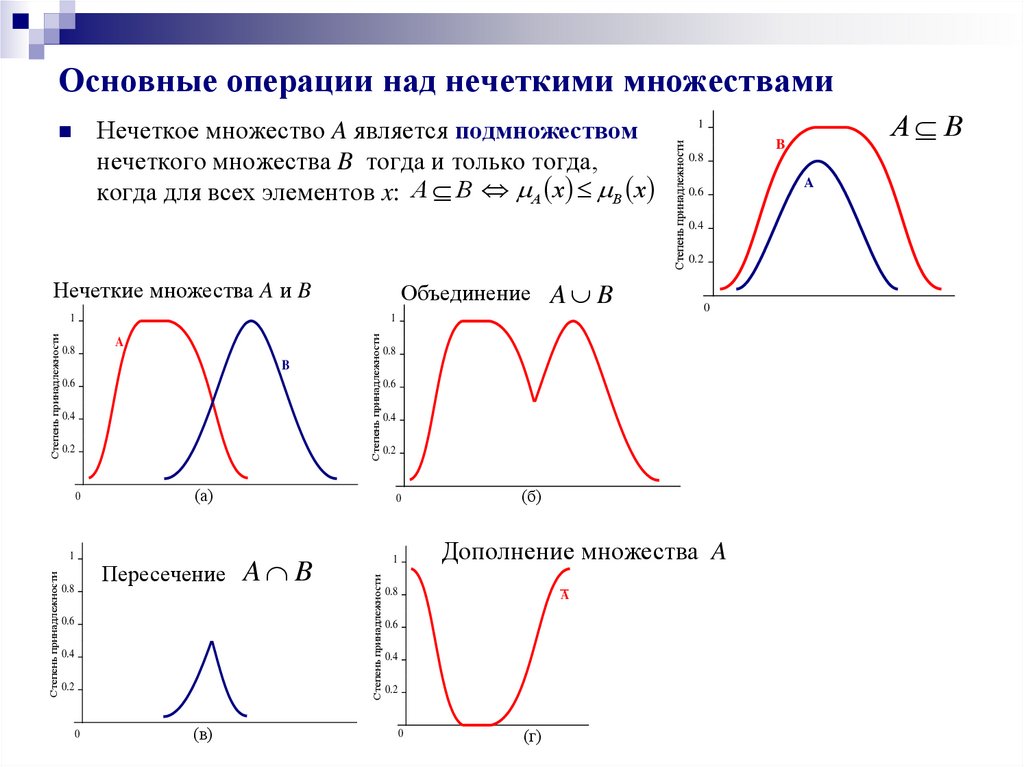
8. Основные операции над нечеткими множествами
Объединение A BНечеткие множества A и B
A
0.8
B
0.6
0.4
0.2
0
Степень принадлежности
1
(а)
Пересечение
0.8
0.6
0.4
0.2
0
Степень принадлежности
1
(в)
A B
B
0.8
A
0.6
0.4
0.2
0
0.8
0.6
0.4
0.2
0
(б)
Дополнение множества A
1
Степень принадлежности
Степень принадлежности
1
0.8
A
0.6
0.4
0.2
0
(г)
A B
1
Степень принадлежности
Нечеткое множество A является подмножеством
нечеткого множества B тогда и только тогда,
когда для всех элементов x: A B A x B x
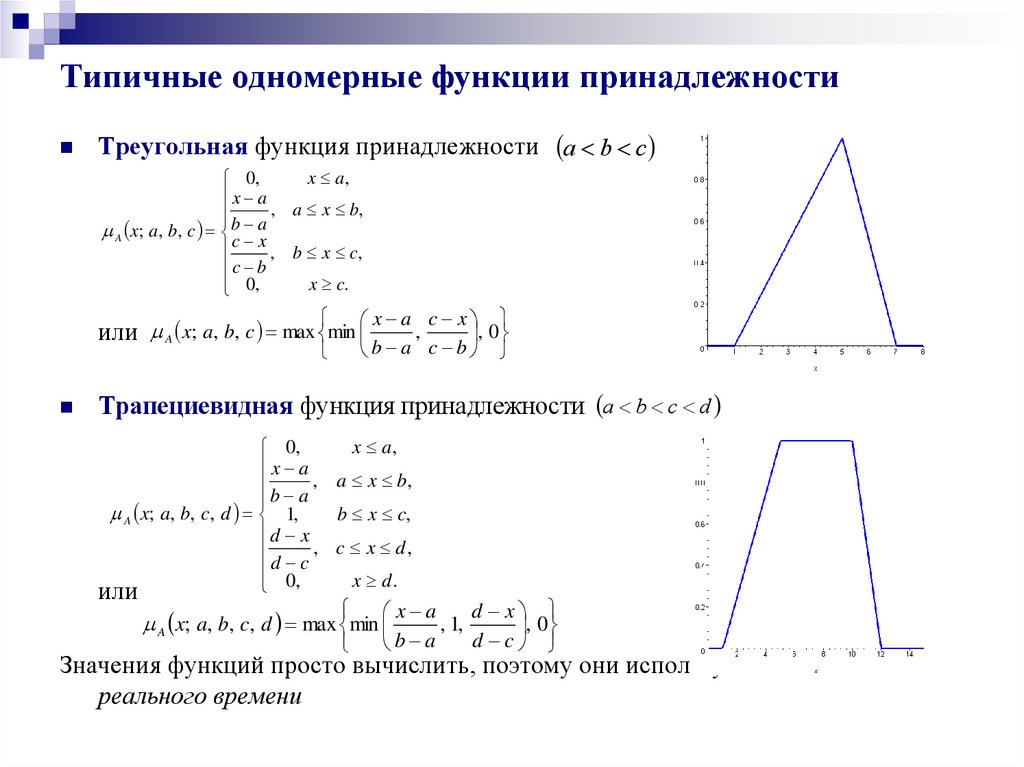
9. Типичные одномерные функции принадлежности
Треугольная функция принадлежности a b cx a,
0,
x a
, a x b,
A x; a, b, c b a
c x
, b x c,
c b
0,
x c.
x a c x
,
, 0
или A x; a, b, c max min
b a c b
Трапециевидная функция принадлежности a b c d
x a,
0,
x a
, a x b,
b
a
A x; a, b, c, d 1,
b x c,
d x
d c , c x d,
0,
x d.
или
d x
x a
, 1,
, 0
b
a
d
c
A x; a, b, c, d max min
Значения функций просто вычислить, поэтому они используются в системах
реального времени
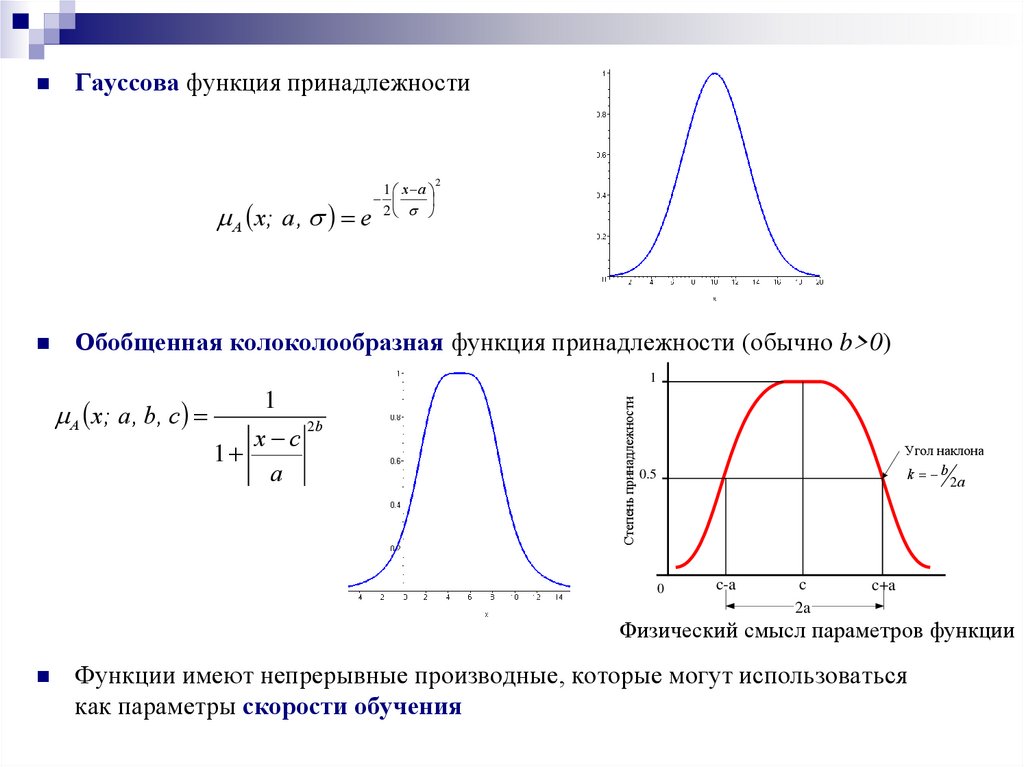
10.
Гауссова функция принадлежностиA x; a , e
1 x a
2
2
Обобщенная колоколообразная функция принадлежности (обычно b>0)
A x; a , b, c
1
x c
1
a
2b
Степень принадлежности
1
Угол наклона
k b
0.5
0
c-a
c
2a
2a
c+a
Физический смысл параметров функции
Функции имеют непрерывные производные, которые могут использоваться
как параметры скорости обучения
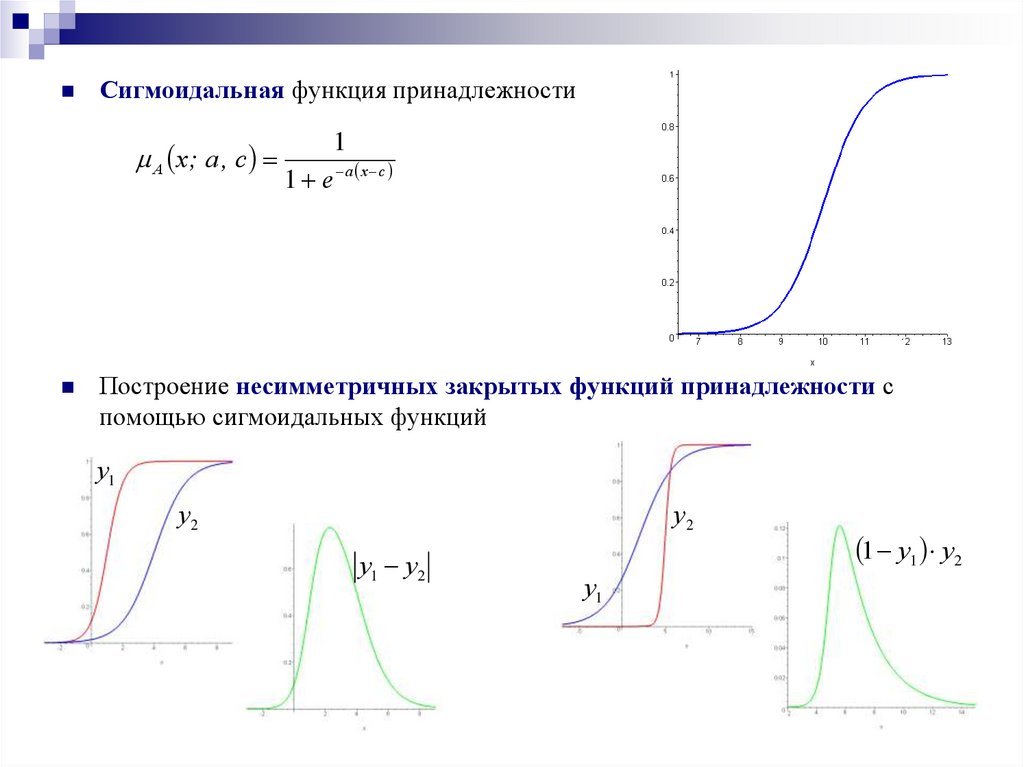
11.
Сигмоидальная функция принадлежностиA x; a , c
1
1 e a x c
Построение несимметричных закрытых функций принадлежности с
помощью сигмоидальных функций
y1
y2
y2
y1 y2
y1
1 y1 y2
12. Заключение
В лекции были рассмотрены элементы теории нечетких множеств:основные определения,
обозначения
операции, используемые в теории нечетких множеств
Приведены примеры типичных функций принадлежности, которые заданы
на поле действительных чисел
Функции принадлежности могут использоваться как функции активации
нейронов в нейронных сетях
В качестве функций принадлежности часто пользуются функциями
плотности распределений вероятностей
На практическом занятии будут рассмотрены:
несимметричные одномерные функции принадлежности,
функции принадлежности в трехмерном пространстве,
операции над нечеткими множествами в трехмерном пространстве
Следующая лекция посвящена применению правил над нечеткими
множествами и методам принятия решений
13. Список литературы
1.Яхъяева Г.Э. Нечеткие множества и нейронные сети. Серия: Основы
информационных технологий. – БИНОМ, 2008. – 320 с.
2.
Jang J.-S., Sun C.T., Mizutani E. Neuro-Fuzzy and Soft Computing: A
Computational Approach to Learning and Machine Intelligence. – The USA:
Prentice Hall, 1997. – 614 p.
3.
Тарков М.С. Нейрокомпьютерные системы. Серия: Основы
информационных технологий. – Изд-во Интернет-университета
информационных технологий – ИНТУИТ.ру, БИНОМ, 2006. – 144 с.





 Математика
Математика








