Похожие презентации:
Геометрическая вероятность
1.
1.Выбор точки из фигуры на плоскости
2.
Выбор точки из отрезка и дуги
окружности
3.
Выбор точки из числового отрезка
2. Выбор точки из фигуры на плоскости Определение геометрической вероятности
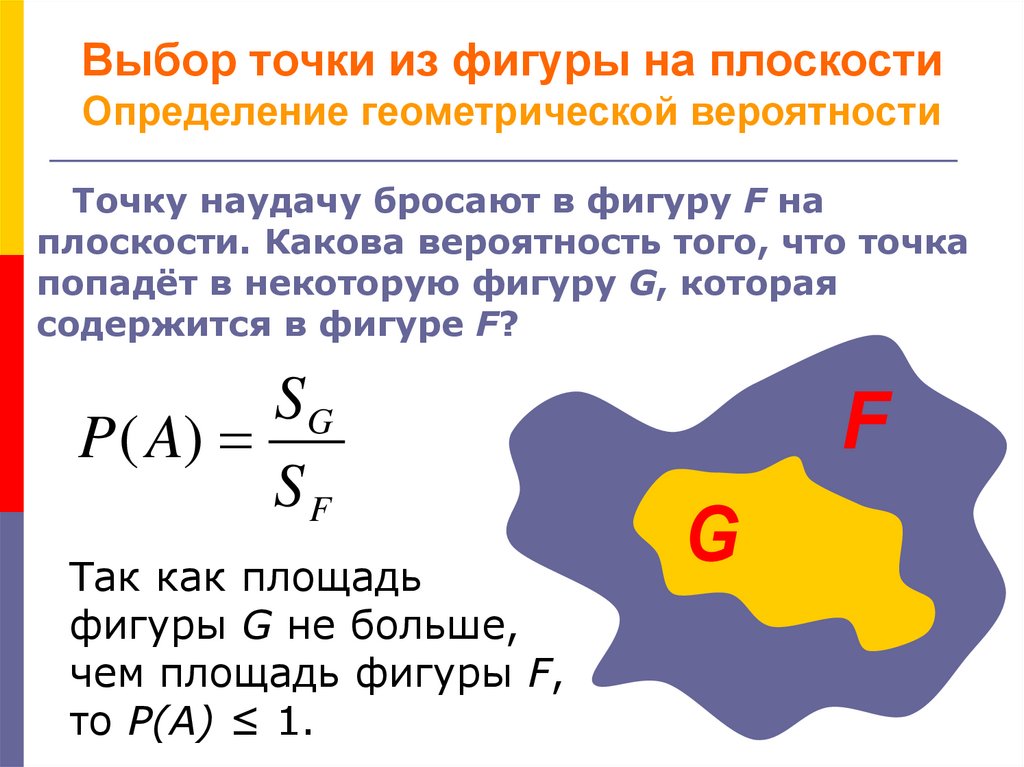
Точку наудачу бросают в фигуру F наплоскости. Какова вероятность того, что точка
попадёт в некоторую фигуру G, которая
содержится в фигуре F?
SG
P ( A)
SF
Так как площадь
фигуры G не больше,
чем площадь фигуры F,
то P(A) ≤ 1.
3. Выбор точки из фигуры на плоскости Пример 1
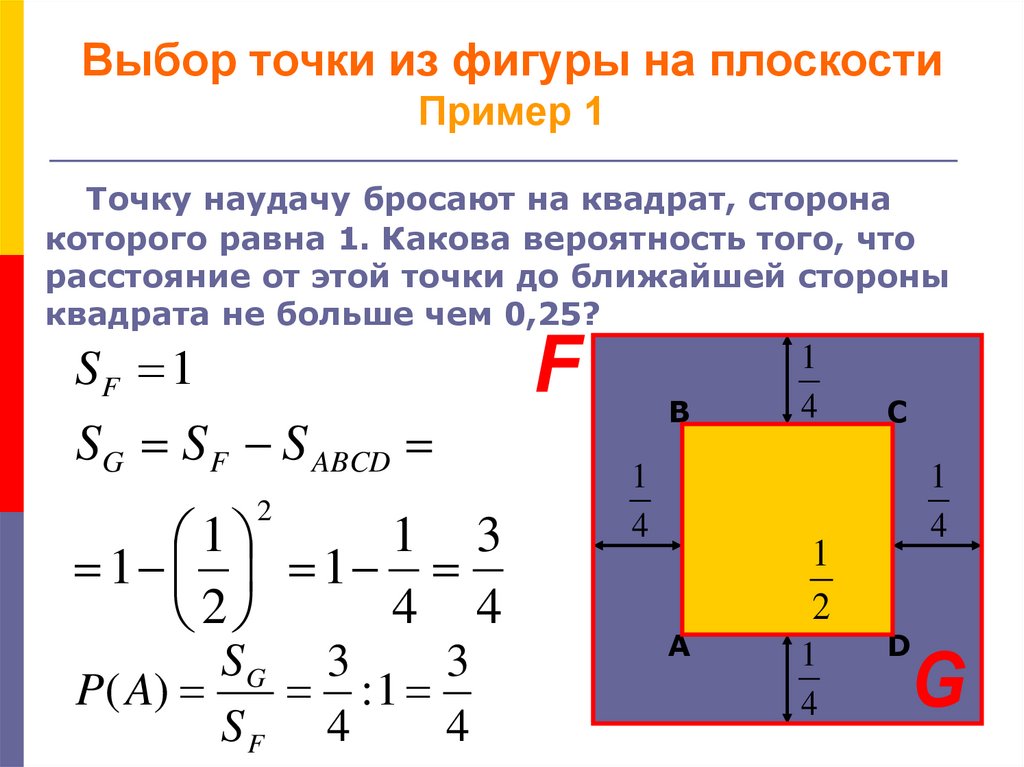
Точку наудачу бросают на квадрат, сторонакоторого равна 1. Какова вероятность того, что
расстояние от этой точки до ближайшей стороны
квадрата не больше чем 0,25?
SF 1
SG S F S ABCD
2
1 3
1
1 1
4 4
2
SG 3
3
P( A)
:1
SF 4
4
B
1
4
1
4
C
1
4
1
2
A
1
4
D
4. Выбор точки из фигуры на плоскости Пример 2
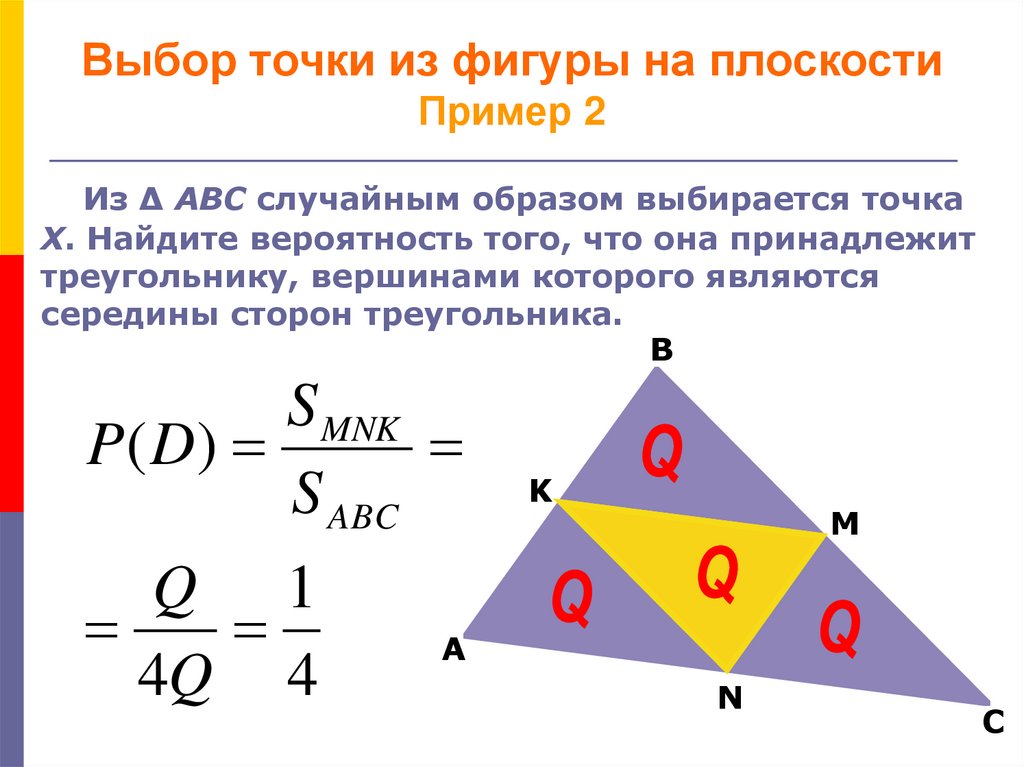
Из ∆ ABC случайным образом выбирается точкаX. Найдите вероятность того, что она принадлежит
треугольнику, вершинами которого являются
середины сторон треугольника.
B
S MNK
P( D)
S ABC
Q 1
4Q 4
K
M
A
N
C
5. Выбор точки из отрезка Пример
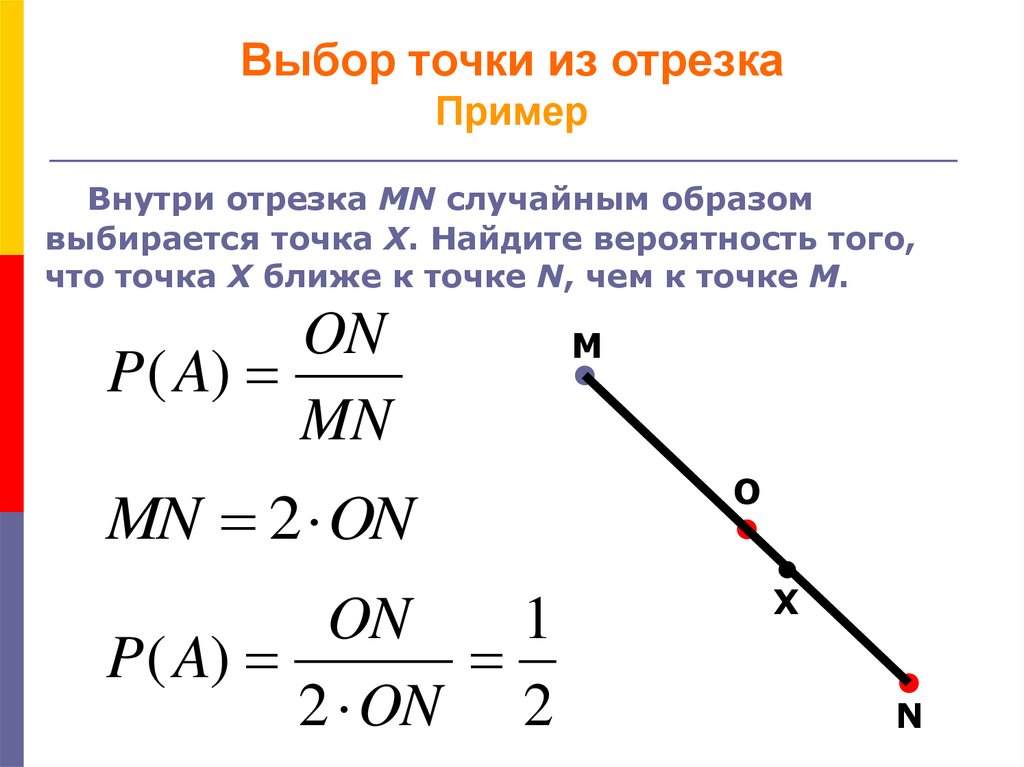
Внутри отрезка MN случайным образомвыбирается точка X. Найдите вероятность того,
что точка X ближе к точке N, чем к точке M.
ON
P ( A)
MN
MN 2 ON
ON
1
P ( A)
2 ON 2
M
O
X
N
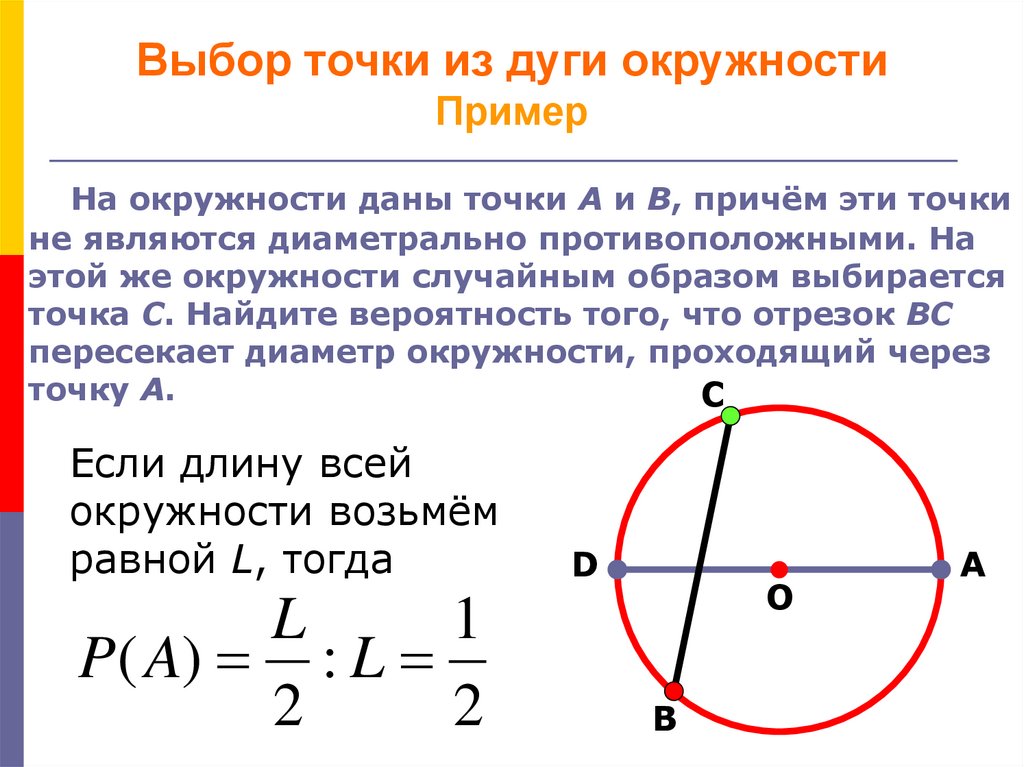
6. Выбор точки из дуги окружности Пример
На окружности даны точки A и B, причём эти точкине являются диаметрально противоположными. На
этой же окружности случайным образом выбирается
точка C. Найдите вероятность того, что отрезок ВС
пересекает диаметр окружности, проходящий через
точку А.
C
Если длину всей
окружности возьмём
равной L, тогда
L
1
P ( A) : L
2
2
D
O
B
A
7. Выбор точки из числового отрезка Определение
xm
a
b
n
Рассмотрим событие, состоящее в том, что
точка с координатой x выбрана из отрезка
[a;b], содержащегося в отрезке [m;n].
Это событие обозначим (a≤x≤b).
А его вероятность равна отношению длин
отрезков [a;b] и [m;n]:
b a
P ( a x b)
n m
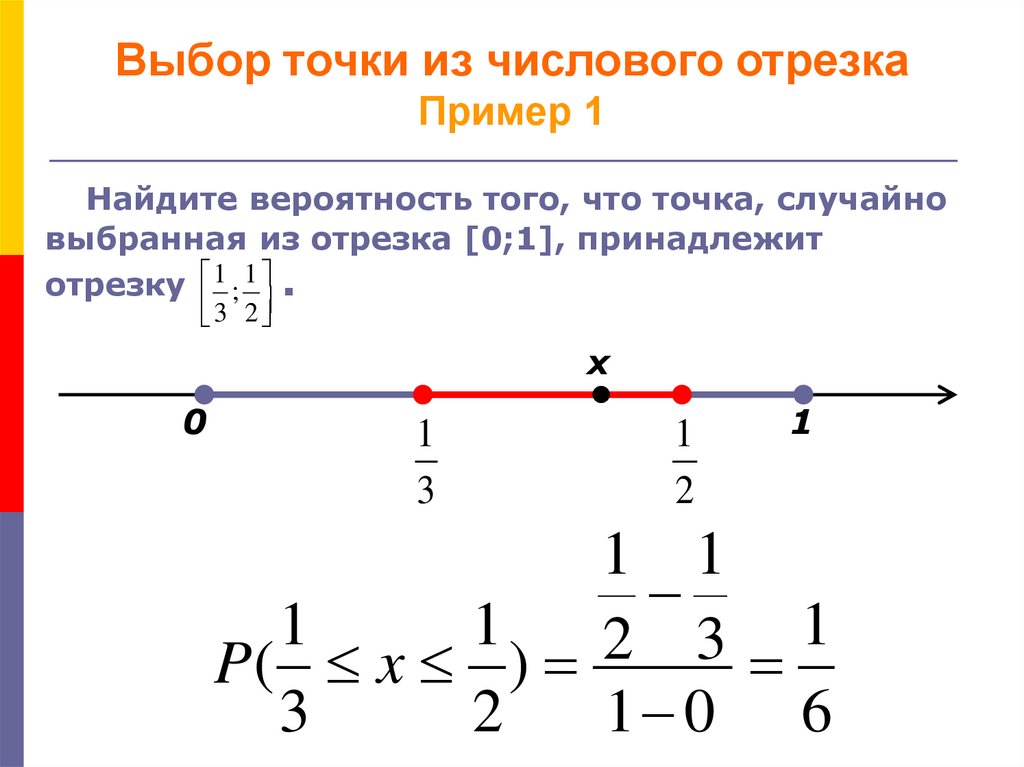
8. Выбор точки из числового отрезка Пример 1
Найдите вероятность того, что точка, случайновыбранная из отрезка [0;1], принадлежит
отрезку 1 ; 1 .
3 2
x
0
1
3
1
2
1
1 1
1
1
1
2
3
P( x )
3
2
1 0 6
9. Выбор точки из числового отрезка Пример 2
Согласно правилам дорожного движения, пешеходможет перейти улицу в неустановленном месте, если в
пределах видимости нет пешеходных переходов. В
городе N расстояние между пешеходными переходами на
улице S равно 1 км. Пешеход переходит улицу S где-то
между этими двумя переходами. Он может видеть знак
перехода не дальше чем за 100 м от себя. Найдите
вероятность того, что пешеход не нарушает правила.
0,9 0,1
P (0,1 x 0,9x)
0,8
1 0
0
0,1
0,9
1
10. Выбор точки из числового отрезка Пример 3
Поезд проходит мимо платформы за полминуты.В какой-то момент, совершенно случайно выглянув
из своего купе в окно, Иван Иванович увидел, что
поезд идёт мимо платформы. Иван Иванович
смотрел в окно ровно 10 секунд, а затем отвернулся.
Найдите вероятность того, что он видел Петра
Петровича, который стоял ровно посередине
платформы.
x
0
5
15
30
15 5 1
P(5 x 15)
30 0 3




 Математика
Математика








