Возможности трехуровневых задач типа «SAM» для организации и проведения промежуточной аттестации школьников. (Занятие 4)

1.

Занятие 4
Возможности трехуровневых задач типа «SAM» для
организации и проведения промежуточной
аттестации школьников. Оценка уровневого
индивидуального прогресса школьников
Заславский Владимир Моисеевич
28 ноября 2016

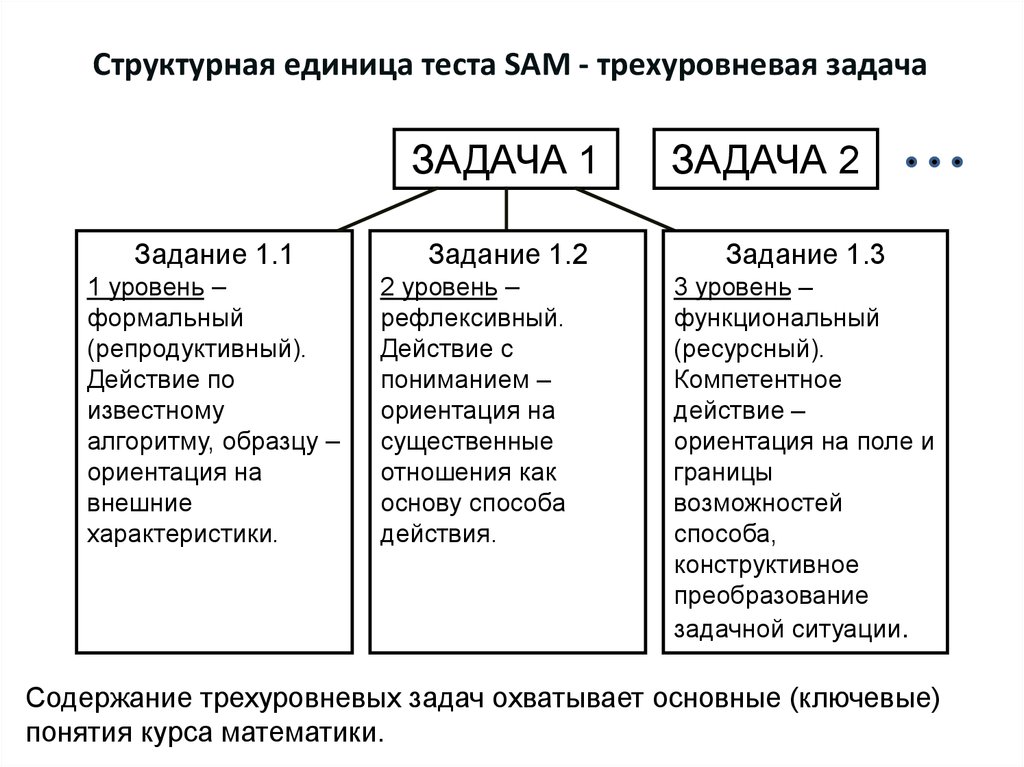
2. Структурная единица теста SAM - трехуровневая задача

ЗАДАЧА 1
Задание 1.1
1 уровень –
формальный
(репродуктивный).
Действие по
известному
алгоритму, образцу –
ориентация на
внешние
характеристики.
Задание 1.2
2 уровень –
рефлексивный.
Действие с
пониманием –
ориентация на
существенные
отношения как
основу способа
действия.
ЗАДАЧА 2
Задание 1.3
3 уровень –
функциональный
(ресурсный).
Компетентное
действие –
ориентация на поле и
границы
возможностей
способа,
конструктивное
преобразование
задачной ситуации.
Содержание трехуровневых задач охватывает основные (ключевые)
понятия курса математики.

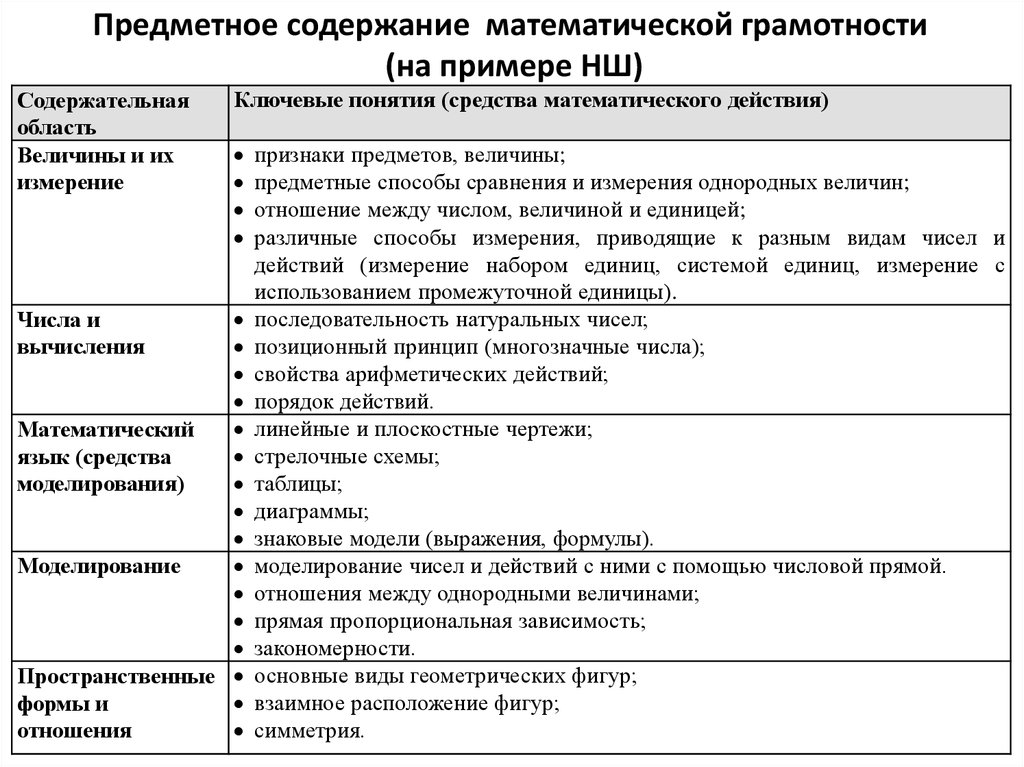
3. Предметное содержание математической грамотности (на примере НШ)

Содержательная
область
Величины и их
измерение
Ключевые понятия (средства математического действия)
Математический
язык (средства
моделирования)
Моделирование
Пространственные
формы и
отношения
Числа и
вычисления
признаки предметов, величины;
предметные способы сравнения и измерения однородных величин;
отношение между числом, величиной и единицей;
различные способы измерения, приводящие к разным видам чисел и
действий (измерение набором единиц, системой единиц, измерение с
использованием промежуточной единицы).
последовательность натуральных чисел;
позиционный принцип (многозначные числа);
свойства арифметических действий;
порядок действий.
линейные и плоскостные чертежи;
стрелочные схемы;
таблицы;
диаграммы;
знаковые модели (выражения, формулы).
моделирование чисел и действий с ними с помощью числовой прямой.
отношения между однородными величинами;
прямая пропорциональная зависимость;
закономерности.
основные виды геометрических фигур;
взаимное расположение фигур;
симметрия.

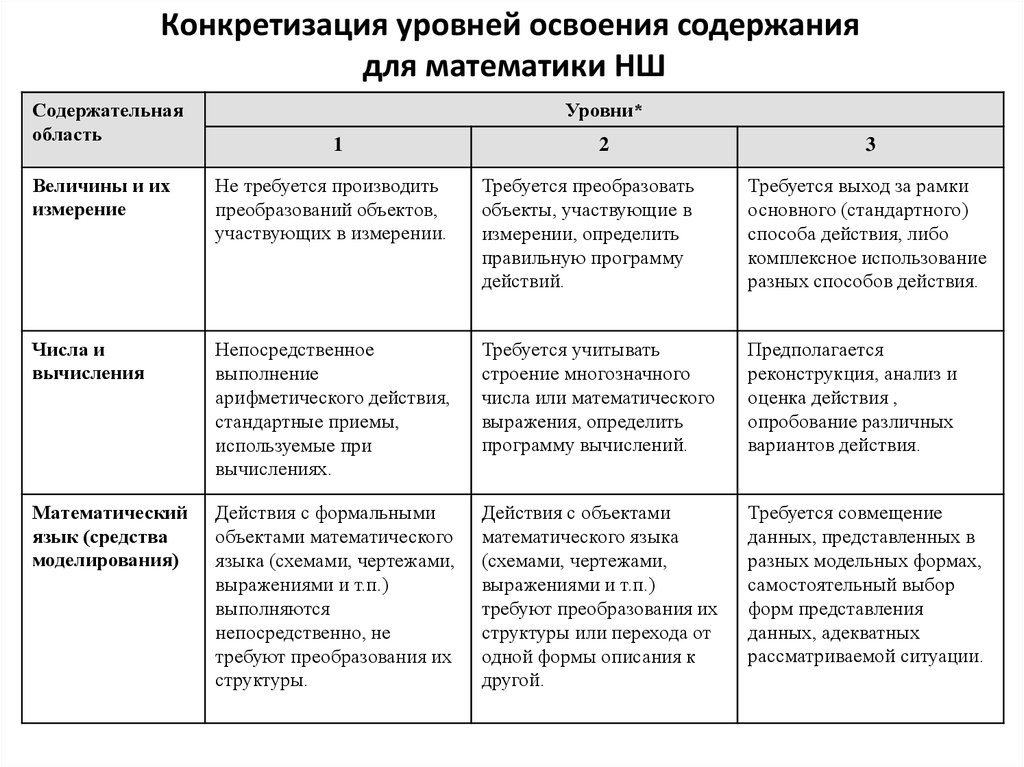
4. Конкретизация уровней освоения содержания для математики НШ

Содержательная
область
Уровни*
1
2
3
Величины и их
измерение
Не требуется производить
преобразований объектов,
участвующих в измерении.
Требуется преобразовать
объекты, участвующие в
измерении, определить
правильную программу
действий.
Требуется выход за рамки
основного (стандартного)
способа действия, либо
комплексное использование
разных способов действия.
Числа и
вычисления
Непосредственное
выполнение
арифметического действия,
стандартные приемы,
используемые при
вычислениях.
Требуется учитывать
строение многозначного
числа или математического
выражения, определить
программу вычислений.
Предполагается
реконструкция, анализ и
оценка действия ,
опробование различных
вариантов действия.
Математический
язык (средства
моделирования)
Действия с формальными
объектами математического
языка (схемами, чертежами,
выражениями и т.п.)
выполняются
непосредственно, не
требуют преобразования их
структуры.
Действия с объектами
математического языка
(схемами, чертежами,
выражениями и т.п.)
требуют преобразования их
структуры или перехода от
одной формы описания к
другой.
Требуется совмещение
данных, представленных в
разных модельных формах,
самостоятельный выбор
форм представления
данных, адекватных
рассматриваемой ситуации.

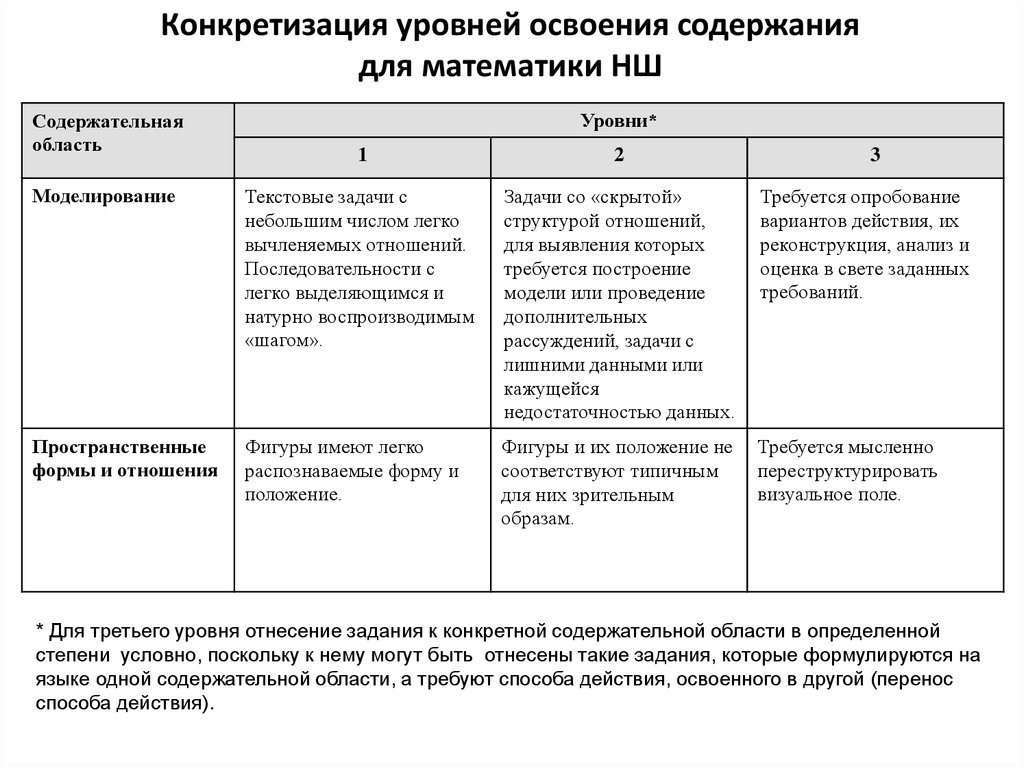
5. Конкретизация уровней освоения содержания для математики НШ

Содержательная
область
Уровни*
1
2
3
Моделирование
Текстовые задачи с
небольшим числом легко
вычленяемых отношений.
Последовательности с
легко выделяющимся и
натурно воспроизводимым
«шагом».
Задачи со «скрытой»
структурой отношений,
для выявления которых
требуется построение
модели или проведение
дополнительных
рассуждений, задачи с
лишними данными или
кажущейся
недостаточностью данных.
Требуется опробование
вариантов действия, их
реконструкция, анализ и
оценка в свете заданных
требований.
Пространственные
формы и отношения
Фигуры имеют легко
распознаваемые форму и
положение.
Фигуры и их положение не
соответствуют типичным
для них зрительным
образам.
Требуется мысленно
переструктурировать
визуальное поле.
* Для третьего уровня отнесение задания к конкретной содержательной области в определенной
степени условно, поскольку к нему могут быть отнесены такие задания, которые формулируются на
языке одной содержательной области, а требуют способа действия, освоенного в другой (перенос
способа действия).

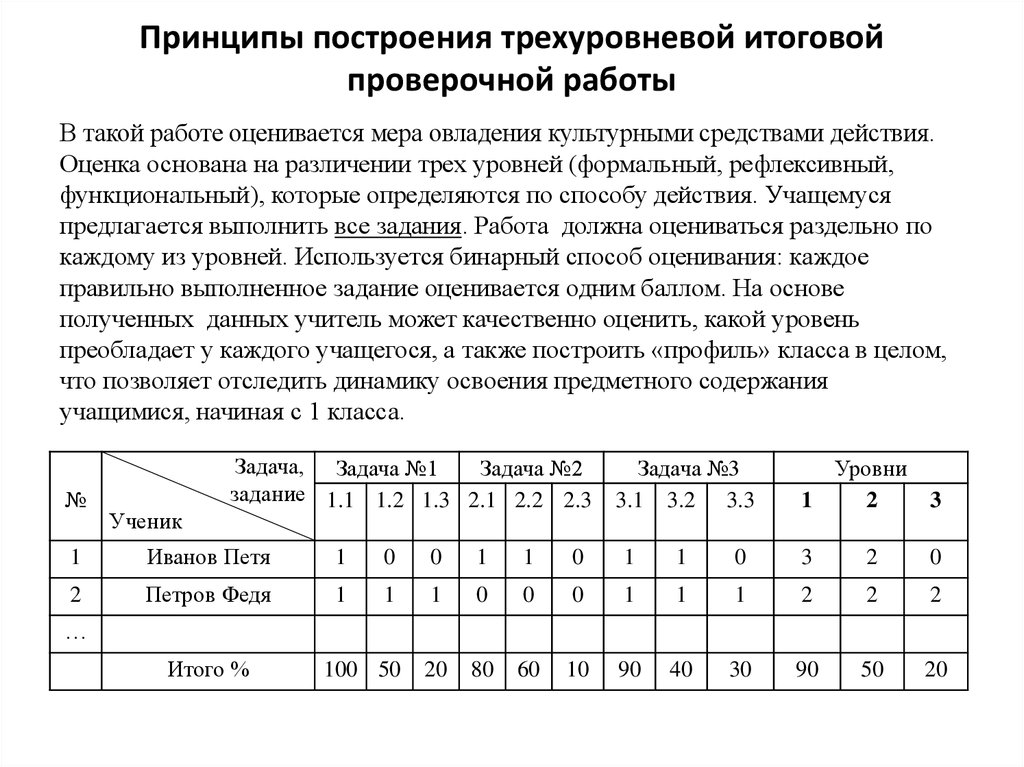
6. Принципы построения трехуровневой итоговой проверочной работы

В такой работе оценивается мера овладения культурными средствами действия.
Оценка основана на различении трех уровней (формальный, рефлексивный,
функциональный), которые определяются по способу действия. Учащемуся
предлагается выполнить все задания. Работа должна оцениваться раздельно по
каждому из уровней. Используется бинарный способ оценивания: каждое
правильно выполненное задание оценивается одним баллом. На основе
полученных данных учитель может качественно оценить, какой уровень
преобладает у каждого учащегося, а также построить «профиль» класса в целом,
что позволяет отследить динамику освоения предметного содержания
учащимися, начиная с 1 класса.
№
Ученик
Задача, Задача №1
Задача №2
задание 1.1 1.2 1.3 2.1 2.2 2.3
Задача №3
3.1 3.2 3.3
Уровни
1
2
3
1
Иванов Петя
1
0
0
1
1
0
1
1
0
3
2
0
2
Петров Федя
1
1
1
0
0
0
1
1
1
2
2
2
100 50
20
80
60
10
90
40
30
90
50
20
…
Итого %

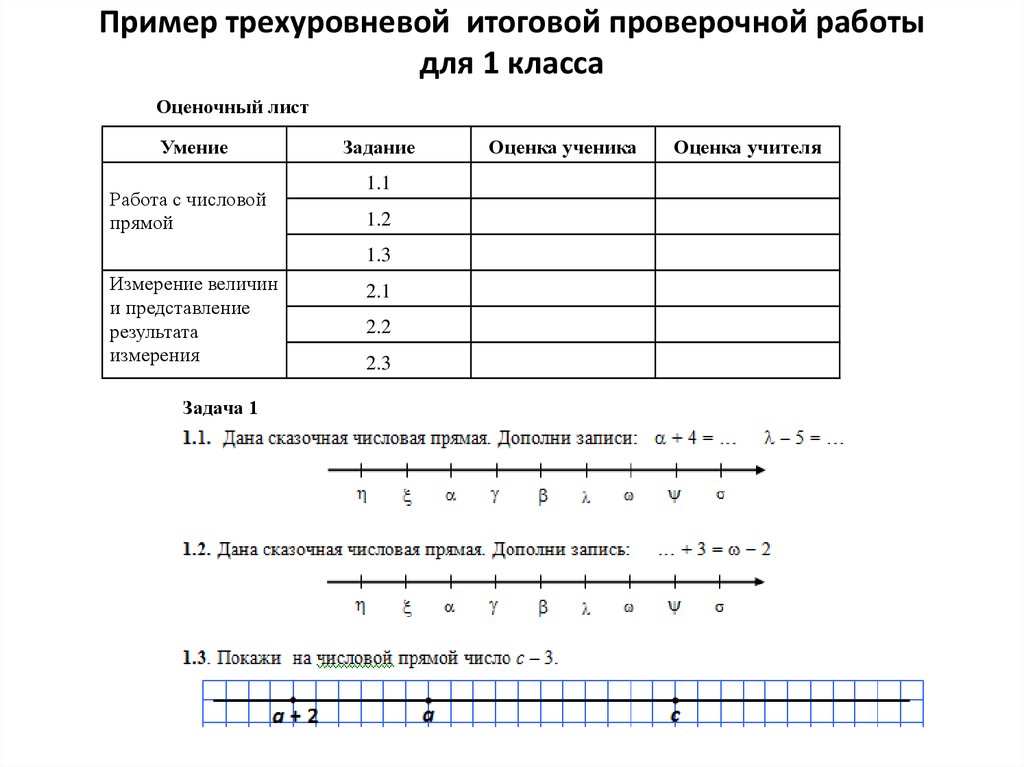
7. Пример трехуровневой итоговой проверочной работы для 1 класса

Оценочный лист
Умение
Работа с числовой
прямой
Задание
1.1
1.2
1.3
Измерение величин
и представление
результата
измерения
Задача 1
2.1
2.2
2.3
Оценка ученика
Оценка учителя

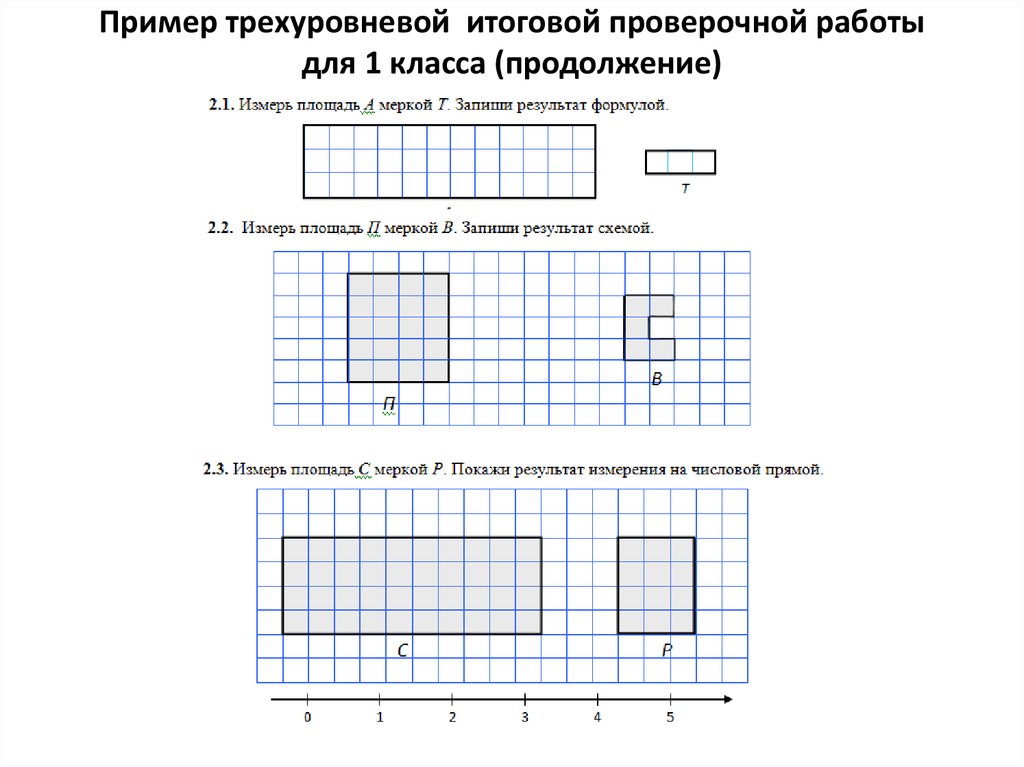
8. Пример трехуровневой итоговой проверочной работы для 1 класса (продолжение)

9. Пример трехуровневой итоговой проверочной работы для 2 класса

Задача
Умение
1
2
Измерение величин в
Сложение
позиционных системах
многозначных чисел
счисления
и
3
вычитание Измерение
помощью
мерки
величин
с
промежуточной

10. Пример трехуровневой итоговой проверочной работы для 2 класса (продолжение)

11. Пример трехуровневой итоговой проверочной работы для 2 класса (продолжение)

12. Пример трехуровневой итоговой проверочной работы для 6 класса

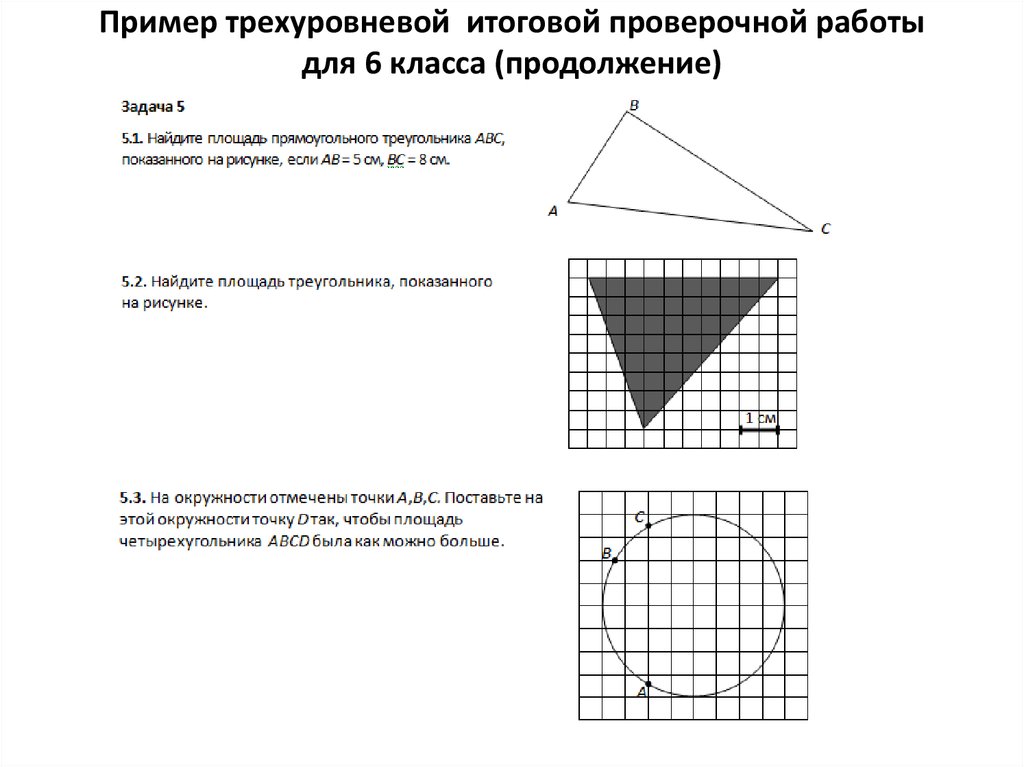
13. Пример трехуровневой итоговой проверочной работы для 6 класса (продолжение)

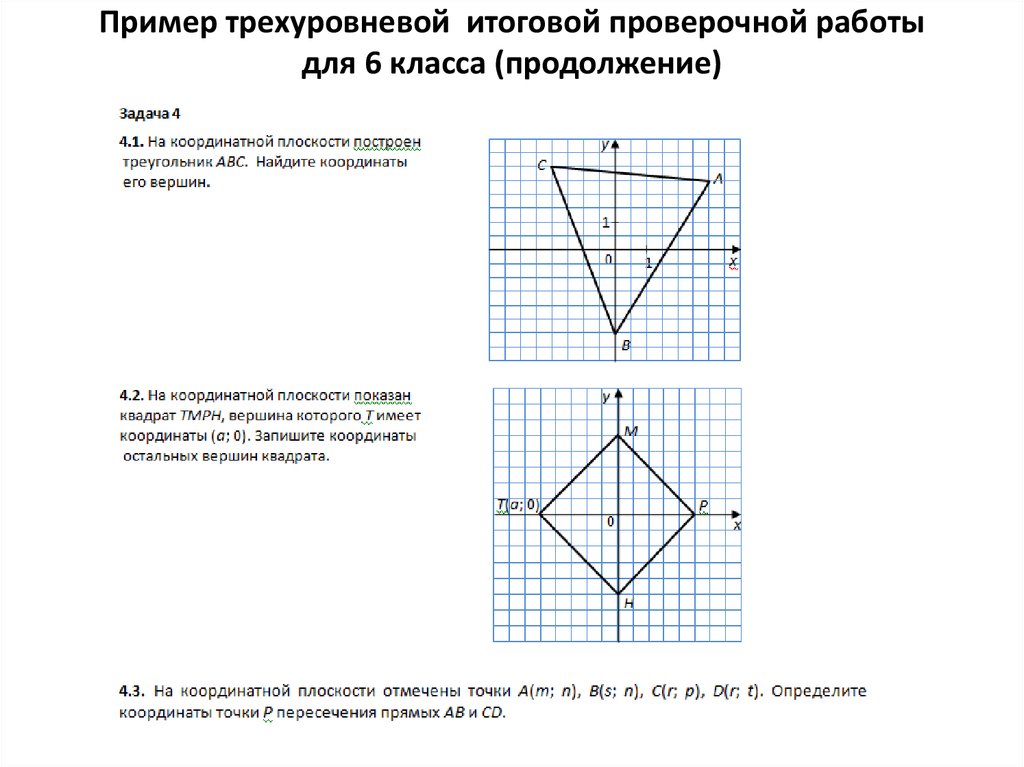
14. Пример трехуровневой итоговой проверочной работы для 6 класса (продолжение)

15. Пример трехуровневой итоговой проверочной работы для 9 класса

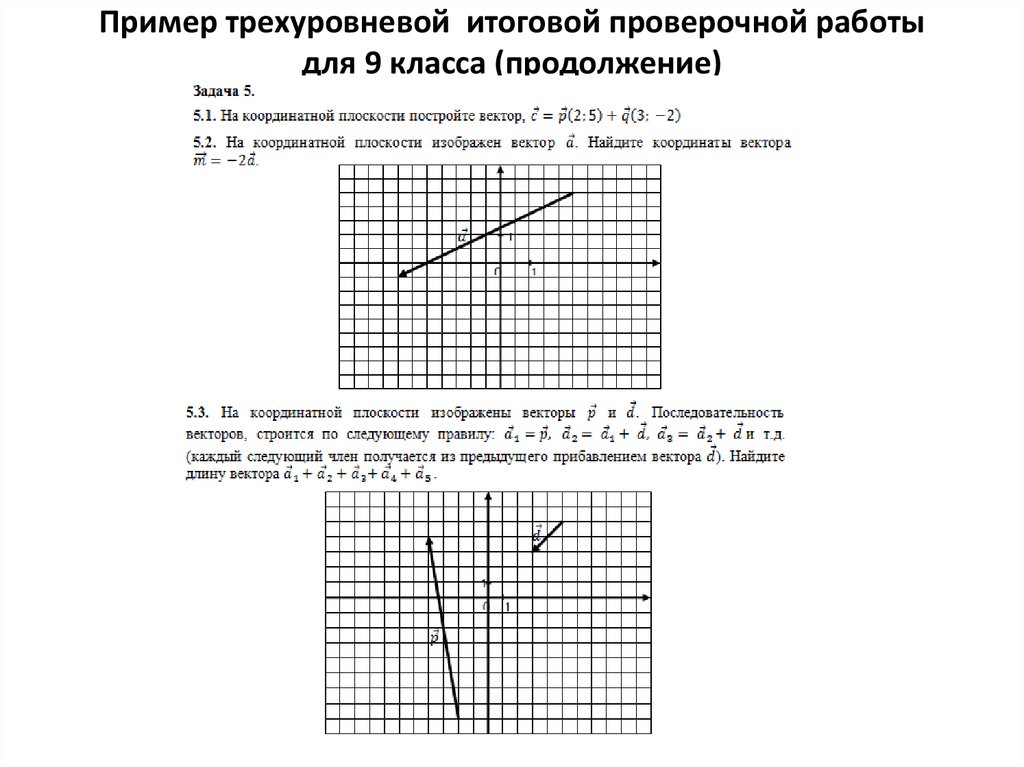
16. Пример трехуровневой итоговой проверочной работы для 9 класса (продолжение)

17. Пример трехуровневой итоговой проверочной работы для 9 класса (продолжение)

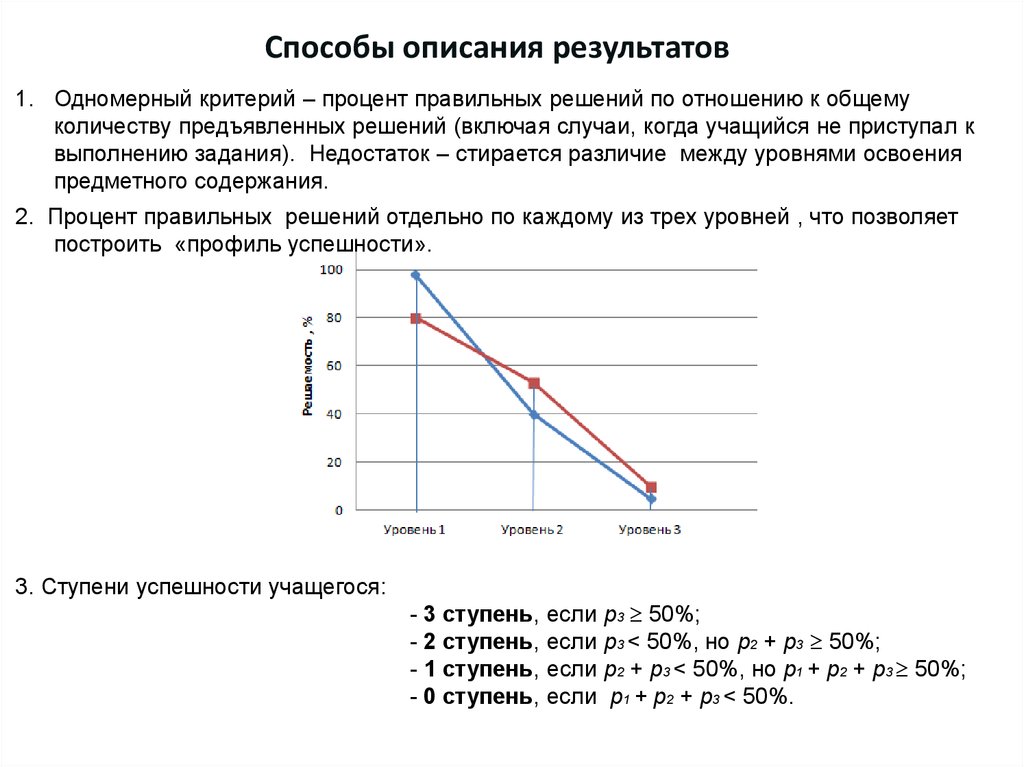
18. Способы описания результатов

1. Одномерный критерий – процент правильных решений по отношению к общему
количеству предъявленных решений (включая случаи, когда учащийся не приступал к
выполнению задания). Недостаток – стирается различие между уровнями освоения
предметного содержания.
2. Процент правильных решений отдельно по каждому из трех уровней , что позволяет
построить «профиль успешности».
3. Ступени успешности учащегося:
- 3 ступень,
- 2 ступень,
- 1 ступень,
- 0 ступень,
если р3 50%;
если р3 < 50%, но р2 + р3 50%;
если р2 + р3 < 50%, но р1 + р2 + р3 50%;
если р1 + р2 + р3 < 50%.

19. Задание 4

Выделить
не
менее
двух
ключевых
математических понятий (способов действия),
изучаемых в течение учебного года (класс – по
выбору). Разработать трехуровневые задачи
для проверки освоения этих понятий.