Мнимая загадочность в поведении игральных кубиков

1. Мнимая загадочность в поведении игральных кубиков

Мелков Артем,
ученик 7Б класса
МОБУ гимназии№1
г.Мелеуза

2. Популярность игры в кости

3. В начале XVII века к великому Галилею явился приятель, который захотел получить разъяснение по следующему поводу. Играя в три

кости, он заметил, что число 10, как
сумма очков на трех костях, появляется чаще чем
число 9.
«Как же так, – спрашивал игрок, – ведь как в
случае девятки, так и в случае десятки эти числа
набираются одинаковым числом способов, а
именно шестью?»

4. Цели и задачи

Цель исследования:
Выяснить какая из возможных сумм при
подбрасывании трех кубиков появляется чаще.
Задачи исследования:
познакомиться с историей игральных кубиков и
задач, возникающих с этими играми;
провести игру-опыт по выявлению наиболее часто
выпадаемой суммы;
провести теоретическое рассуждение о суммах,
которые выпадают при подбрасывании трех
игральных кубиков.

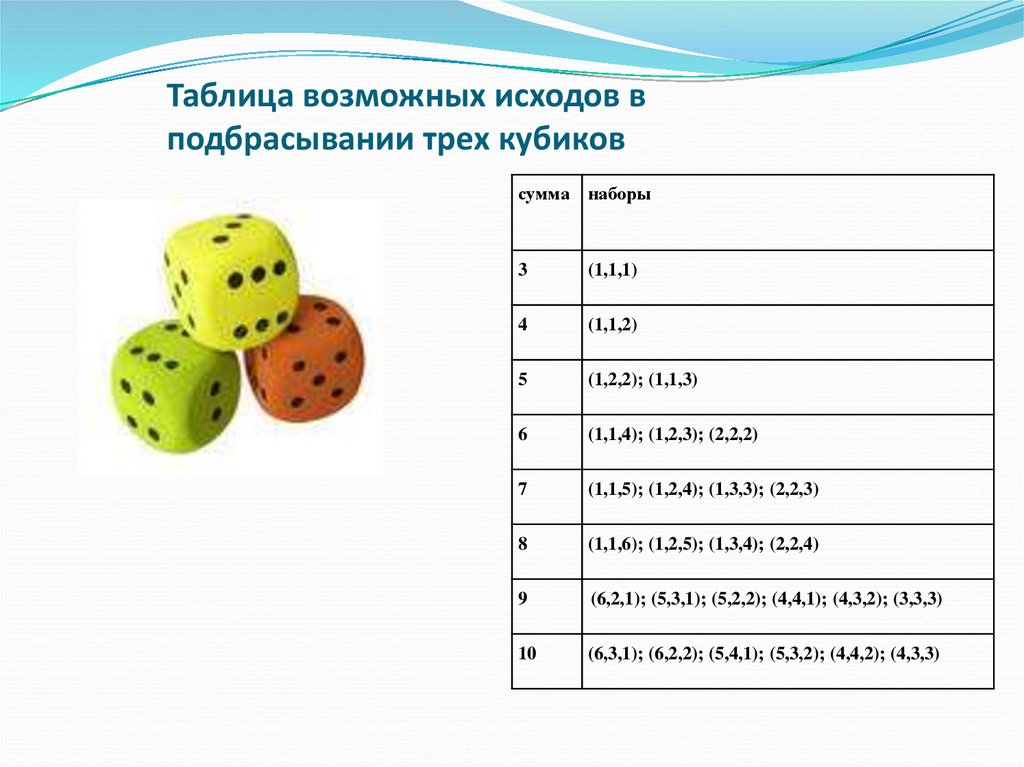
5. Таблица возможных исходов в подбрасывании трех кубиков

сумма наборы
3
(1,1,1)
4
(1,1,2)
5
(1,2,2); (1,1,3)
6
(1,1,4); (1,2,3); (2,2,2)
7
(1,1,5); (1,2,4); (1,3,3); (2,2,3)
8
(1,1,6); (1,2,5); (1,3,4); (2,2,4)
9
(6,2,1); (5,3,1); (5,2,2); (4,4,1); (4,3,2); (3,3,3)
10
(6,3,1); (6,2,2); (5,4,1); (5,3,2); (4,4,2); (4,3,3)

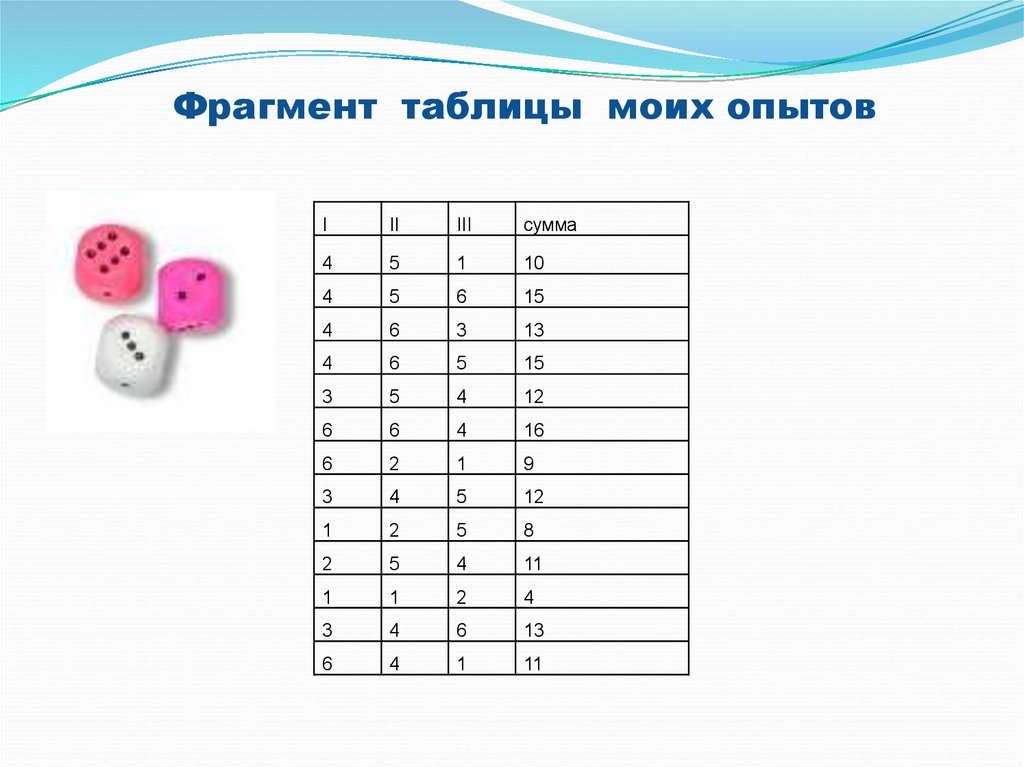
6.

Фрагмент таблицы моих опытов
I
II
III
сумма
4
5
1
10
4
5
6
15
4
6
3
13
4
6
5
15
3
5
4
12
6
6
4
16
6
2
1
9
3
4
5
12
1
2
5
8
2
5
4
11
1
1
2
4
3
4
6
13
6
4
1
11

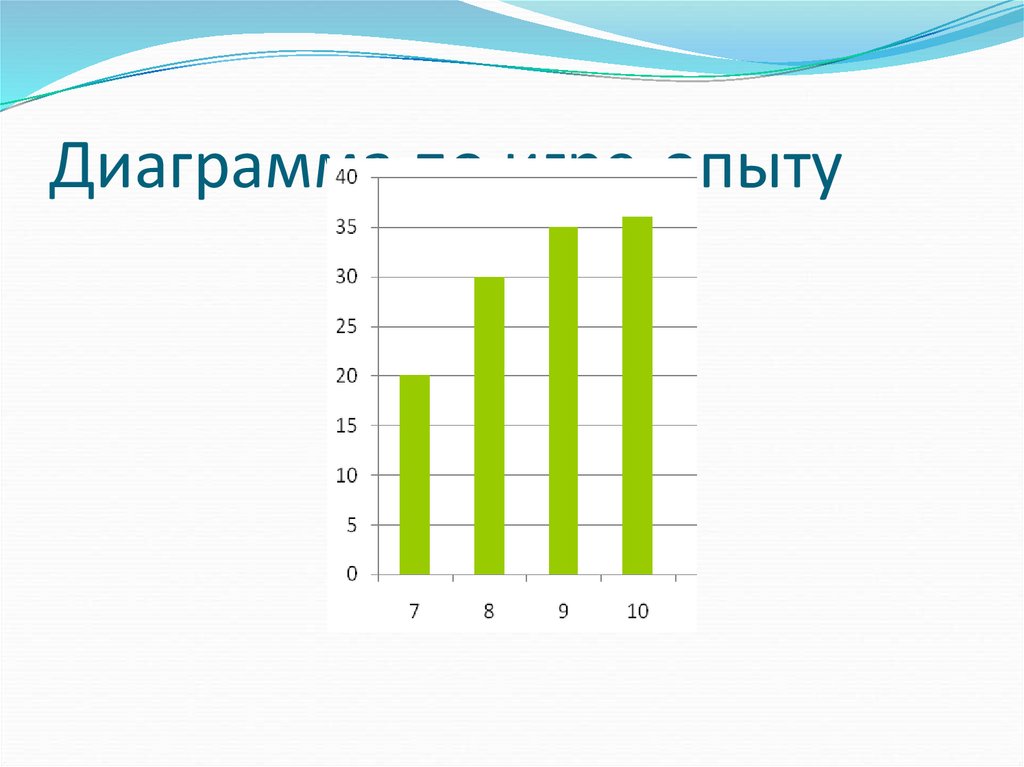
7. Диаграмма по игре-опыту

8. Первые опыты на компьютере

№
1
2
3
сумма
сколько раз встречается в
опыте
1
3
4
3
10
159
2
5
3
6
14
3
2
2
5
9
141
4
2
4
4
10
159
5
5
6
5
16
6
2
1
5
8
133
7
1
2
5
8
133
8
5
1
2
8
133
9
1
5
1
7
85
10
1
2
6
9
141
11
3
5
2
10
159
12
2
2
5
9
141
13
3
5
6
14
14
1
3
3
7
15
6
5
2
13
85

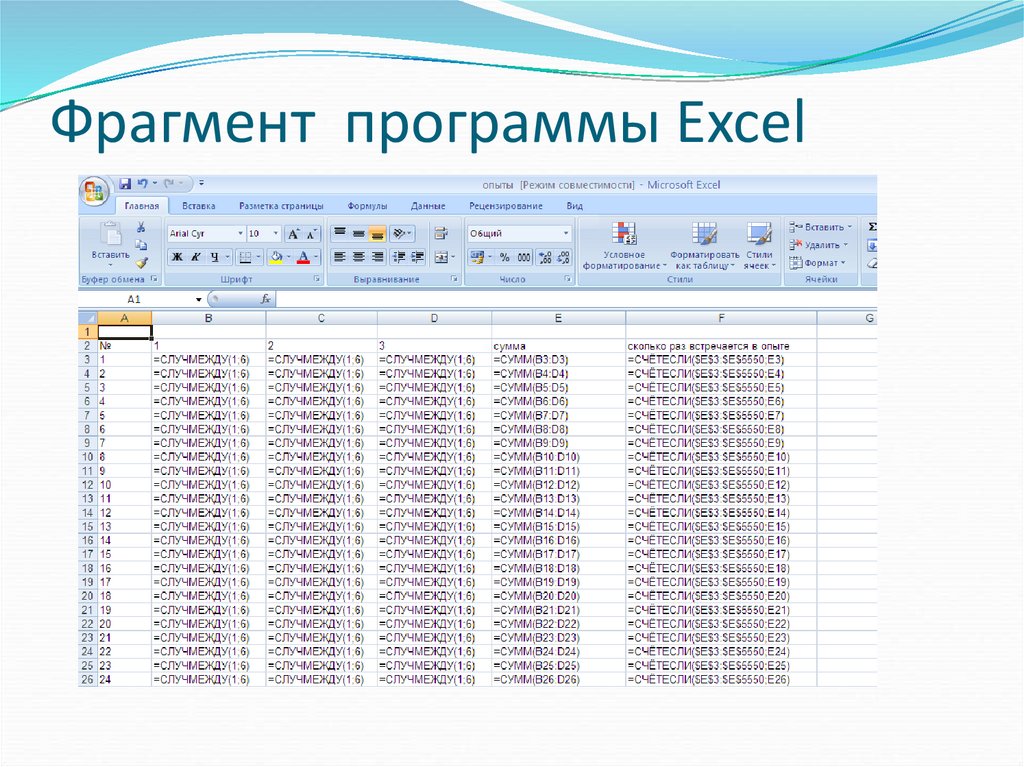
9. Фрагмент программы Excel

10. Итоги

№
5273
5274
5275
5276
5277
5278
5279
5280
5281
5282
5283
5284
5285
I
6
6
4
5
2
5
4
3
2
5
5
3
2
II
4
2
4
1
6
1
3
5
5
3
6
5
1
III
1
2
1
3
2
2
5
2
2
2
3
1
4
сумма
11
10
9
9
10
8
12
10
9
10
14
9
7
сколько раз
встречается
742
663
663
742
742
663
742
663

11. Сравнение

Сумма 9
(6; 2 ;1)
( 5 ; 3 ;1)
(5;2 ;2)
(4; 4 ;1)
(4;3;2)
(3;3 ;2)
Сумма 10
(6; 3 ;1)
(6; 2 ; 2)
( 5 ; 4 ;1)
(5;3;2)
(4;4;2)
(4;3;3)

12. Итоговые комбинации

(6;2;1), (6;1;2),(2;6;1),(2;1;6),
(1;6;2), (1;2;6)
(6;3;1), (6;1;3),(3;6;1),(3;1;6),
(1;6;3), (1;3;6)
(5;3;1), (5;1;3), (3;1;5), (3;5;1),
(1;5;3), (1;3;5)
(5;4;1), (5;1;4), (4;1;5), (4;5;1),
(1;5;4), (1;4;5)
(4;3;2), (4;2;3), (3;2;4), (3;4;2),
(2;3;4), (2;4;3)
(5;3;2), (5;2;3), (3;2;5), (3;5;2),
(2;3;5), (2;5;3)
(5;2;2), (2;5;2), (2;2;5)
(6;2;2), (2;6;2), (2;2;6)
(4;1;1), (1;4;1), (1;1;4)
(4;3;3), (3;4;3), (3;3;4)
(3;3;3)
(2;4;4), (4;2;4), (4;4;2)

13. Выводы

история игральных кубиков уходит корнями в
историю древнего мира, когда кубики
использовались для развлечений, гаданий и
предсказаний;
достоверность некоторого факта (появление суммы
10) можно проверить лишь очень большим
количеством опытов;
загадочность в поведении игральных кубиков
является «мнимой», так как появление суммы 10
является закономерностью.