Похожие презентации:
Системы счисления
1.
СИСТЕМЫСЧИСЛЕНИЯ
2.
СИСТЕМЫ СЧИСЛЕНИЯСистемой счисления называется
совокупность символов (цифр) и
правил их использования для
представления чисел
3.
СИСТЕМЫ СЧИСЛЕНИЯСистемы
счисления
Позиционные
Непозиционные
4.
НЕПОЗИЦИОННЫЕ СИСТЕМЫСЧИСЛЕНИЯ
Римская система счисления:
I-1
Значение цифры не зависит от ее
положения в числе
Величина числа определяется как сумма
или разность чисел
Если меньшая цифра стоит слева от
большей, то она вычитается
Если меньшая цифра стоит справа от
большей, то она прибавляется
V-5
X - 10
L - 50
C – 100
D - 500
M - 1000
5.
РИМСКАЯ СИСТЕМАСЧИСЛЕНИЯ
Пример
1998 = МСМXCVIII, где
М = 1000
СМ = 1000 – 100 = 900
XC = 100 – 10 = 90
VIII = 5+1+1+1=8
Задание
Запишите римскими цифрами числа:
2002, 4044, 1024
6.
ПОЗИЦИОННЫЕСИСТЕМЫ СЧИСЛЕНИЯ
• Значение цифры зависит от ее
позиции в числе
• Позиция цифры называется
разрядом
• Основание системы равно
количеству цифр, используемых ею
7.
ПОЗИЦИОННЫЕ СИСТЕМЫСЧИСЛЕНИЯ
Любое число, записанное в позиционной
системе счисления с произвольным
основанием, можно записать в виде
полинома:
A(S)=anS^n+an-1S^n-1+…+a0S^0+a-mS^m
Пример
345 = 3*10^2+4*10^1+5*10^0
Задание
Записать в виде полинома числа 444, 228,
8.
ПОЗИЦИОННЫЕ СИСТЕМЫСЧИСЛЕНИЯ
• За основание позиционной системы счисления можно
принять любое натуральное число большее 1
• Для записи чисел в позиционной системе с
основанием n нужно иметь алфавит из n цифр
Основание
Система
Алфавит
2
Двоичная
01
3
Троичная
012
8
Восьмеричная
01234567
16
Шестнадцатеричная
0123456789ABCDEF
9.
СИСТЕМЫ СЧИСЛЕНИЯ И ЭВМПринцип Неймана:
ЭВМ выполняет арифметические расчеты в двоичной системе счисления
Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед
другими системами:
·
для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть
ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как
в десятичной;
·
представление информации посредством только двух состояний надежно и
помехоустойчиво;
·
возможно применение аппарата булевой алгебры для выполнения логических
преобразований информации;
·
двоичная арифметика намного проще десятичной.
10.
МОДЕЛЬ ПЕРЕВОДАЧИСЕЛ ИЗ ОДНОЙ
СИСТЕМЫ
СЧИСЛЕНИЯ В
ДРУГУЮ
11.
ПЕРЕВОД ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫСЧИСЛЕНИЯ В ЛЮБУЮ ДРУГУЮ
Чтобы перевести целое положительное
десятичное число в систему счисления с
другим основанием, нужно это число
разделить на основание. Полученное
частное снова разделить на основание, и
дальше до тех пор, пока частное не
окажется меньше основания. В результате
записать в одну строку последнее частное и
все остатки, начиная с последнего
12.
ПЕРЕВОД ИЗ ДЕСЯТИЧНОЙСИСТЕМЫ СЧИСЛЕНИЯ В ЛЮБУЮ ДРУГУЮ
Пример
Пример
Пример
4410=?2
88810=?8
120210=?16
44/2=22 (ост.0)
888/8=111 (ост.0)
1202/16=75 (ост.2)
22/2=11 (ост.0)
111/8=13 (ост.7)
75/16=4 (ост.11)
11/2=5 (ост.1)
13/8=1 (ост.5)
120210=4B216
5/2=2 (ост.1)
88810=15708
2/2=1 (ост.0)
4410=1011002
13.
ПЕРЕВОД ИЗ ЛЮБОЙ СИСТЕМЫСЧИСЛЕНИЯ В ДЕСЯТИЧНУЮ
Для того чтобы число из любой
системы счисления перевести в
десятичную систему счисления,
необходимо его представить в
развернутом виде и произвести
вычисления
Развернутый вид:
A(S)=anS^n+an-1S^n-1+…+a0S^0+a-mS^m
14.
ПЕРЕВОД ИЗ ЛЮБОЙСИСТЕМЫ СЧИСЛЕНИЯ В ДЕСЯТИЧНУЮ
Пример
1011012=?10
543210
1011012 = 1*2^5+0*2^4+1*2^3+1*2^2+0*2^1+1*2^0=32+8+4+1=4510
64248=?10
3210
64248=6*8^3+4*8^2+2*8^1+4*8^0=3072+256+16+4=334810
15.
ПЕРЕВОД ИЗ ДВОИЧНОЙ СИСТЕМЫ ВСИСТЕМУ С ОСНОВАНИЕМ «СТЕПЕНЬ
Для преобразования двоичного числа
ДВОЙКИ»
в число с основанием «степень
двойки» необходимо двоичную
последовательность разбить на группы
по количеству цифр равному степени
справа налево и каждую группу
заменить соответствующей цифрой
новой системы счисления
16.
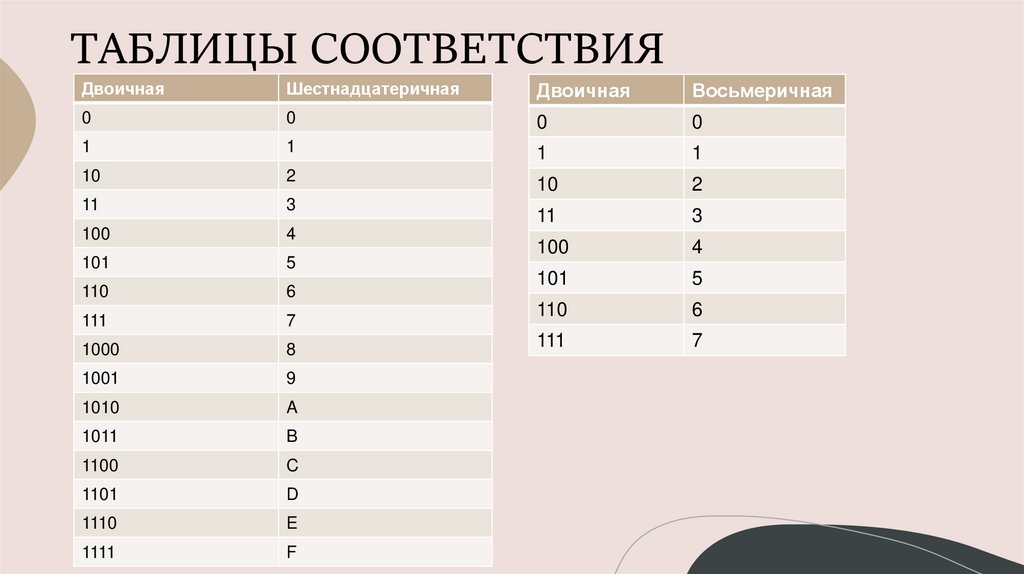
ТАБЛИЦЫ СООТВЕТСТВИЯДвоичная
Шестнадцатеричная
Двоичная
Восьмеричная
0
0
0
0
1
1
1
1
10
2
10
2
11
3
11
3
100
4
101
5
100
4
110
6
101
5
111
7
110
6
1000
8
111
7
1001
9
1010
A
1011
B
1100
C
1101
D
1110
E
1111
F
17.
ПЕРЕВОД ИЗ СИСТЕМЫ С ОСНОВАНИЕМ«СТЕПЕНЬ ДВОЙКИ» В ДВОИЧНУЮ
Этот перевод аналогичен предыдущему,
выполненному в обратную сторону: каждую
цифру мы заменяем группой цифр в
двоичной системе из таблицы соответствия
18.
Пример10110101010111101012=?8=?16
2^x=8 ------>x=3
10110101010111101012= 1 011 010 101 011 110 101 = 13253658
2^x=16 ------>x=4
10110101010111101012= 101 1010 1010 1111 0101 = 5AAF516
19.
1. Перевести из десятичной системы в двоичную числа: 144, 806,1808
2. Перевести из десятичной системы в восьмеричную числа: 282,
1812, 12450
3. Перевести из десятичной системы в шестнадцатеричную числа:
512, 1024, 2048
4. Перевести из шестнадцатеричной системы в десятичную числа:
666, 4E24, 41E8
5. Перевести из восьмеричной системы в десятичную числа: 2610,
4657, 42708
6. Перевести из двоичной системы в десятичную числа: 1101000,
11011110, 11111100110
20.
7. Перевести из двоичной системы в восьмеричнуючисла: 1010100, 11100011, 110111011
8. Перевести из двоичной системы
в шестнадцатеричную числа: 10110101101, 1111010,
101110
9. Перевести из восьмеричной системы в двоичную
числа: 122, 777,422
10. Перевести из шестнадцатеричной системы
в двоичную числа: 84, 3Е, 2F



















 Информатика
Информатика








