Похожие презентации:
Сигналы, обеспечивающие повышенную помехозащищенность
1.
кафедра информационнотелекоммуникационных систем и технологийДисциплина Анализ информационной
безопасности телекоммуникационных систем
Тема 4 Сигналы, обеспечивающие повышенную
помехозащищенность и скрытность
телекоммуникационных систем
профессор
Белов Сергей Павлович
1
2.
ЦЕЛЬЮ темы является - изучение особенностей формированияузкополосных и широкополосных сигналов. Особое внимание
при
рассмотрении
узкополосных
сигналов
уделено
сигнально-кодовым
конструкциям,
имеющим
высокую
спектральную
эффективность.
При
рассмотрении
широкополосных сигналов основное внимание уделено
сигналам, полученным на основе применения специальных
кодов и новых методов расширения спектра.
ЗАДАЧИ лекции:
1 изучение особенностей широкополосных сигналов
Литература
1. Белов, С.П., Жиляков, Е.Г. Анализ информационной безопасности
телекоммуникационных
систем:
Учебно-методический
комплекс. : http://pegas.bsu.edu.ru/course/view.php?id=8360
Белгород, 2015 год.
3.
Все рассмотренные выше классические методы узкополосной модуляцииразработаны с целью достижения максимальной спектральной
эффективности, т. е. передачи информации с возможно большей
скоростью в возможно более узкой полосе частот. Проблема заключается
в том, что с увеличением числа пользователей число каналов,
выделенных для связи, должно возрастать. В то же время, очевидно, что,
с одной стороны, общий частотный ресурс является ограниченной
величиной, а, с другой стороны, невозможно бесконечно уменьшать
полосу частот, в которой осуществляется передача информации. В
инфокоммуникационных системах с простыми сигналами эффективность
использования частотного ресурса дополнительно снижается за счет
того, что при большой неопределенности частоты и изменениях времени
прихода принимаемых сигналов для снижения взаимных помех
приходится вводить защитные интервалы по частоте.
Следовательно, уменьшение затрат ресурсов на одного пользователя
может быть достигнуто только на основе принципиально иного подхода к
проблеме.
4.
Одним из подходов, позволяющих кардинально увеличить число пользователей вограниченном частотном диапазоне и значительно улучшить качество приема в
условиях многолучевого распространения радиоволн, является использование
модулированных сигналов с расширенным спектром, иначе называемых сигналами с
шумоподобным спектром или широкополосными шумоподобными канальными
сигналами (ШШКС). Отличительной особенностью этих сигналов является величина
базы сигнала Б, которая по определению равна произведению длительности
передаваемого информационного символа (
) на полосу частот, в которой он
передается ( F ). Если у рассматриваемых выше (узкополосных) сигналов эта величина
примерно равна единицы, т.е. Б= * F ≈1, так как F ≈ 1/
, то у ШШКС Б >> 1.
Широкополосность у этих сигналов определяется не абсолютным значением ширины
его спектра, а величиной базы. Величину базы ШШКС можно рассматривать как
некоторый параметр, характеризующий сознательно вводимую в сигнал избыточность.
Именно она и определяет ряд специфических свойств этих сигналов, которые
открывают возможность для создания систем передачи информации, обладающих
весьма ценными качествами.
Применение ШШКС позволяет реализовать инфокоммуникационные системы, с
помощью которых успешно решают следующие задачи:
1) получение высокой достоверности передачи цифровой информации в условиях
многолучевого распространения сигналов;
2) обеспечение высокой
помехоустойчивости к организованным
помехам и
возможность криптостойкой и имитостойкой передачи особо важной информация
(Термины «криптостойкость» и «имитостойкость» происходят от латинских слов crypto
— тайный, скрытый и imitation — повторение, подделка. Они характеризуют скрытность
передачи и трудность ее расшифровки, а также трудность создания помех, похожих на
передаваемые сигналы, для дезориентации получателя информации).
5.
3) эффективное использование выделенного диапазона частот при одновременнойработе в этом диапазоне многих систем, т. е. обеспечение электромагнитной
совместимости различных систем, использующих один и тот же диапазон частот.
B литературе ШШКС называют как: широкополосные, псевдослучайные,
шумоподобные, составные и т.д. Каждый из этих терминов отображает какую-то из
особенностей таких сигналов, связанных с их свойствами или методами получения. В
дальнейшем будем пользоваться термином «сложный сигнал» как наиболее общим.
При выборе необходимой величины базы сложного сигнала нужно различать два
случая: 1) ∆fэ= const, 2) = const.
В первом случае задана ширина спектра сложного сигнала. Такое положение
возникает, если имеются ограничения на ширину используемого диапазона частот. В
этом случае нужное значение базы можно получить, только увеличивая длительность
информационного символа
(а, следовательно, и длительность посылки сложного
сигнала). При этом с увеличением базы (увеличением ) скорость передачи будет
падать. Следовательно, применение сложных сигналов в данном случае связано с
уменьшением информативности системы и может быть оправдано в таких каналах, где
информативность не имеет первостепенного значения и в первую очередь необходимо
обеспечить высокую помехоустойчивость (каналы синхронизации, командные линии).
Во втором случае задана длительность информационного символа
(а,
следовательно, и длительность соответствующей ему посылки сложного сигнала). При
таком условии требуемую величину базы можно обеспечить только соответствующим
выбором ширины спектра сложного сигнала. Скорость передачи в этом случае остается
постоянной и при соответствующем значении
может быть весьма высокой.
Применение сложных сигналов в данном случае может оказаться целесообразным в
каналах, где отсутствуют ограничения на ширину полосы частот, но имеются случайные
изменения параметров (например, в тропосферных каналах).
6.
В графическом виде сложные сигналы можно представить следующим образомРисунок 1 Вид сложного сигнала с длительностью информационного импульса и
длительностью элемента псевдослучайной последовательности (ПСП) 0
Используя данные, приведенные на рисунке мы можем найти базу этого сигнала
Б= *(1/
)= * f э ,т.е. Б= /
=9. Естественно, в реальных инфокоммуникационных
системах значения баз колеблется в пределах от десятков единиц до сотен тысяч и
более. Как легко видеть это зависит от объема частотного ресурса используемой
системы. Трудности технического порядка, с переходом на цифровые методы
формирования и обработки сигналов, были устранены.
Следует отметить, что существенное ограничение на количество используемых сложных
сигналов накладывает необходимость выполнения ряда требований, предъявляемых к
ним. Рассмотрим эти требования.
Допустим, что в системе передачи цифровой информации используется п различных
форм сложных сигналов s1(t), s2(t).....sj(t), sn(t). Каждой из форм сигнала на входе
приемника соответствует колебание, представляющее собой сумму этой формы,
искаженной в общем случае из-за неидеальных условий распространения в среде, и
флюктуационного шума, т. е. yj(t)=si(t)+n(t).
7.
Анализируя поступившее на вход колебание yj(t), приемник должен «решить», какая жепосылка содержится в принятом колебании. Это задача распознавания п возможных
сигналов или, иными словами, задача принятия одной гипотезы из п возможных.
Из теории статистических решений известно (а на частном примере различения двух
сигналов, подробно рассмотренном в курсе Общей теории связи, мы убедились в
этом), что все статистически оптимальные процедуры различения n дискретных
сигналов при наличии шума сводятся к сравнению n корреляционных интегралов:
0
I k yi (t ) Sk (t )dt
(1)
0
вычисляемых для всех значений k=1, 2, ..., j, ..., п. В (1) yj(t)—принятое колебание,
образованное одной из форм сигнала и шумом; Sk(t) —образец сигнала, хранящийся в
приемнике.
Если колебание yj(t) образовано посылкой Sk(t) и шумом, то при правильно
выбранных сигналах с большой вероятностью должно выполняться условие:
0
0
y (t )S (t )dt 0 yi (t ) Sk (t )dt , при
k
k
j k
(2)
0
Выполнение этого условия означает, что набор сложных сигналов обладает хорошими
корреляционными свойствами, т.е.:
0
0
S (t )S (t )dt S (t )S (t )dt , при
k
0
k
j
k
j k
(3)
0
Условие (3) показывает, что значение автокорреляционной функции сигнала при
нулевом
сдвиге
(τ=0)
должно
существенно
превышать
значения
взаимнокорреляционных функций.
8.
Напомним, что автокорреляционной функцией сигнала Sk (t) конечной длительностиназывается выражение
а ( )
1 0
S (t ) S (t )dt
k
k
0 0
а взаимно корреляционной функцией сигналов Sj (t) и Sk (t) выражение
При τ=0 имеем a B , что эквивалентно условию (3).
Иными словами, автокорреляционная функция сложного сигнала должна содержать
один значительный максимум (пик), а взаимно-корреляционная функция в любой
момент времени — иметь существенно меньшую величину.
С большой вероятностью подобными свойствами обладают корреляционные и
взаимнокорреляционных
функции
реализаций
нормального
шума
конечной
длительности. Поэтому структура сложных сигналов должна быть такой, чтобы их
корреляционные свойства приближались к аналогичным свойствам отрезков шума. Изза такого сходства сложные сигналы часто называют псевдошумными или
шумоподобными.
Итак, первым требованием к сложным сигналам является получение «хороших»
корреляционных свойств совокупности форм такого сигнала. В соответствии с этим
требованием автокорреляционная функция сигнала должна иметь один значительный
основной пик и минимальные остатки (боковые лепестки). Примерный вид
желательной автокорреляционной и взаимнокорреляционной функции сложного
сигнала длительностью τ0 показан на рисунке 2,а и б соответственно.
9.
Рисунок 2. Автокорреляционная и взаимнокоррелияционная функцииС учетом изложенного возникает естественный вопрос — нельзя ли в качестве
необходимых посылок сложного сигнала использовать набор независимых шумовых
реализаций конечной длительности?
Обладая требуемыми корреляционными свойствами, шумовые реализации вместе с
тем имеют крупный недостаток, связанный с их большим пик фактором. Как известно,
пик фактором колебания kП называют отношение максимальной величины этого
колебания Xmax к эффективному значению Xэф. Применительно к сигналам можно
записать
S
k П max или
k П2 РПик / РС ,
(4)
S эф
где Рпик — пиковая мощность; Рс — средняя мощность сигнала.
10.
Нетрудно видеть, что kП ≥ 1. В реальных условиях необходимо считаться сограниченностью пиковой мощности сигнала. В таких условиях сигналы с пик
фактором, приближающимся к единице, обеспечивают хорошее использование
мощности передатчика (высокий к. п. д. передатчика), а сигналы с большим пик
фактором - плохое. Таким образом, шумовые реализации с энергетической точки
зрения применять нецелесообразно.
Итак, вторым требованием к сложным сигналам является хорошее использование
мощности передатчика.
Одним из важных условий успешного использования систем со сложными сигналами
является необходимость оптимального (или близкого к нему подоптимального) приема
информации. Сложность реализации такого приема до сих пор одна из основных
трудностей, препятствующих более широкому внедрению указанных систем в практику.
Как было установлено ранее, для реализации оптимального приема необходимо
располагать «образцами» используемых сигналов. Поэтому сложные сигналы должны
допускать возможность воспроизведения их «образцов» на приемной стороне линии
связи.
Помимо перечисленных, важным условием приема сложных сигналов является их
четкая синхронизация.
Итак, сложные сигналы должны: 1) иметь большую базу; 2) обладать «хорошими»
корреляционными свойствами; 3) иметь сравнительно небольшой пик фактор, т. е.
обеспечивать хорошую «энергетику» излучаемого сигнала; 4) обеспечивать
возможность воспроизведения в приемнике «образцов» используемых сигналов; 5)
обеспечивать возможность четкой и надежной синхронизации в приемном устройстве.
11.
Псевдослучайные последовательностиНеобходимо отметить, что в инфокоммуникационных системах с расширением спектра
с передачей опорного сигнала может использоваться истинно случайный кодовый
сигнал для расширения и сужения, поскольку кодовый сигнал и модулированный
данными кодовый сигнал одновременно передаются в разных областях спектра. Метод
хранения опорного сигнала не позволяет использовать истинно случайные кодовые
сигналы, поскольку код должен храниться или генерироваться приемником. В таких
системах должен применяться псевдошумовой или псевдослучайный кодовый сигнал.
В чем отличие псевдослучайного кода от истинно случайного? Случайная
последовательность непредсказуема и может быть описана только в статистическом
смысле. Псевдослучайный код на самом деле не является случайным — это
детерминированный периодический сигнал, известный передатчику и приемнику. Так
почему же он называется "псевдослучайным"? Причина в том, что он имеет все
статистические свойства дискретного белого шума. Для "неуполномоченного"
пользователя такой сигнал будет казаться абсолютно случайным.
Каким должен быть псевдослучайный код, чтобы казаться истинно случайным?
Существует
три
основных
свойства
любой
периодической
двоичной
последовательности, которые могут быть использованы в качестве проверки на
случайность.
1. Сбалансированность. Для каждого интервала последовательности количество
двоичных единиц должно отличаться от числа двоичных нулей не больше чем на один
элемент.
2. Цикличность. Циклом называют непрерывную последовательность одинаковых
двоичных чисел. Появление иной двоичной цифры автоматически начинает новый
цикл. Длина цикла равна количеству цифр в нем. Желательно, чтобы в каждом
фрагменте последовательности приблизительно половину составляли циклы обоих
типов длиной 1, приблизительно одну четверть — длиной 2, приблизительно одну
восьмую — длиной 3 и т. д.
12.
3. Корреляция. Если часть последовательности и ее циклично сдвинутая копияпоэлементно сравниваются, желательно, чтобы число совпадений отличалось от числа
несовпадений не более чем на единицу.
Для проверки данных свойств с помощью линейного регистра сдвига сгенерируем
псевдослучайную последовательность.
13.
Здесь крайний левый бит является самым крайним. Проверим полученнуюпоследовательность
на
предмет
соответствия
введенным
критериям.
Последовательность содержит семь нулей и восемь единиц, что соответствует условию
сбалансированности. Рассмотрим циклы нулей — всего их четыре, причем половина их
имеет длину 1, а одна четвертая — длину 2. То же получаем для циклов единиц.
Последовательность слишком коротка, чтобы продолжать проверку, но видно, что
условие цикличности выполняется. Условие корреляции будет проверено ниже.
Последовательность, сгенерированная регистром сдвига, зависит от количества
разрядов, места подсоединения отводов обратной связи и начальных условий.
Последовательности на выходе генератора могут классифицироваться как имеющие
максимальную или не максимальную длину. Период повторения (в тактах)
последовательности максимальной длины, генерируемой m-каскадным линейным
регистром сдвига с обратной связью был приведен выше.
Очевидно, что последовательность, сгенерированная регистром сдвига на рис.
12.7, является примером последовательности с максимальной длиной. Если длина
последовательности меньше, говорят, что последовательность имеет не максимальную
длину.
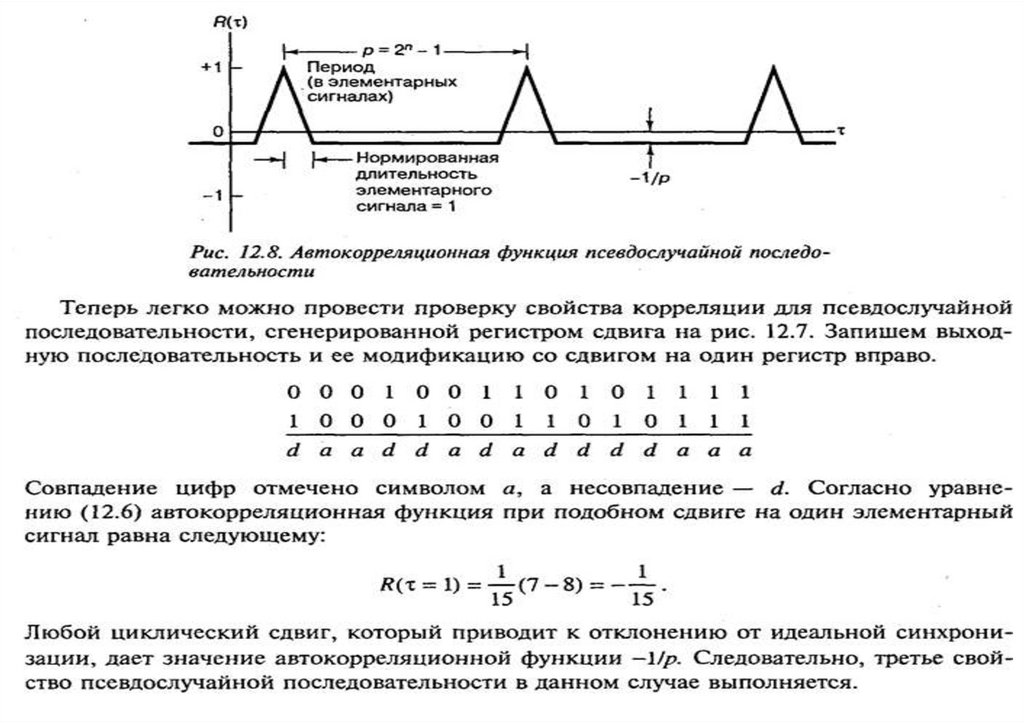
График нормированной автокорреляционной функции последовательности
максимальной длины показан на рис. 12.8. Очевидно, что когда сигнал x(t) и его копия
идеально совпадают, значение автокорреляционной функции равно 1. В то же время
для любого циклического сдвига между x(t) и x(t + τ) при (1 < τ <М) автокорреляционная
функция равна 1/М (для больших значений М- последовательности практически
декоррелируют между собой при сдвиге на один элементарный сигнал).













 Электроника
Электроника








