Похожие презентации:
Теория передачи сигналов
1.
ТЕОРИЯ ПЕРЕДАЧИСИГНАЛОВ
2.
ЛИТЕРАТУРА№
Наименование,
кол-во экземпляров в
библиотеке
1
Теория и техника передачи
информации
[Электронный
ресурс] : учебное пособие для
студентов
вузов
https://biblioclub.ru/index.php?p
age=book_view&book_id=2089
52
2
Теория электрической связи: Андреев Р.Н.,
курс лекций
Краснов Р.П.,
[Электронный ресурс]
Чепелев М.Ю.
https://e.lanbook.com/book/5567
5#authors
3
Теория передачи сигналов на
железнодорожном транспорте:
учебник [Электронный ресурс]
http://e.lanbook.com/books/eleme
nt.php?pl1_id=58968
Место
Используется
Автор(ы)
издания,
при изучении
издательство,
разделов
год
(из п. 4.3)
Акулиничев Ю. Томск: Томск. Все разделы
П.,
гос.
ун-т курса
Бернгардт А. С. систем упр. и
радиоэлектро
ники, 2012
ред.
Г.
Горелов.
Издательство
"Горячая
линияТелеком",
2014.
Все разделы
курса
В. М.:
УМЦ Все разделы
ЖДТ, 2013.
курса
3.
№ Наименование,кол-во экземпляров в библиотеке
Автор(ы)
4
Радиотехнические
цепи
и
сигналы Богомолов С.И.
[Электронный
ресурс]
http://e.lanbook.com/books/element.php?pl1_ci
d=25&pl1_id=10876
5
Радиотехнические цепи и сигналы
[Электронный ресурс]
http://e.lanbook.com/books/element.php?pl1_ci
d=25&pl1_id=10852
Теория передачи сигналов на ж. д.
транспорте: учебник 261 экз.
6
7
8
Место
издания,
издательств
о, год
М.:ТУСУР,
2012.
Каратаева Н.А., М.:ТУСУР,
Ворошилин Е.П. 2010.
Использует
ся
при
изучении
разделов
(из п. 4.3)
4-8
6-7
Под
ред. М.,
Все
Горелова Г. В.
«Транспорт разделы
», 1999 г.
курса
Теория связи в виртуальной лаборатории: Баженов Н. Н.
Омск,
4-8
учебное пособия. 114 экз. + [Электронный
ОмГУПС,
ресурс]
2007г.
http://bibl.omgups.ru/METMAT/Баженов621.39.Б16.zip
Связь на «Последней миле»: Конспект Баженов Н. Н.
лекций. 146 экз. + [Электронный ресурс]
http://bibl.omgups.ru/METMAT/Баженов621.39.zip
Омск,
ОмГУПС,
2011г.
Все
разделы
курса
4.
5.
6.
7.
8.
МодуляцияМодуляция состоит в том, что один из параметров сигнала
изменяется во времени в соответствии с передаваемым
сообщением.
Сигнал у которого изменяется параметр называется сигнал –
переносчик.
В каналах связи в основном используются два вида сигналов –
переносчиков: гармонический сигнал и импульсная
последовательность.
При гармонической модуляции получаем
амплитудную (АМ)
А(t ) A0 AU (t )
частотную (ЧМ)
фазовую (ФМ)
0 U (t )
0 U (t )
9.
АМЧМ
10.
Импульсные виды модуляции бывают следующие:амплитудно-импульсная (АИМ),
широтно-импульсная (ШИМ),
фазо-импульсная (ФИМ)
частотно-импульсная (ЧИМ).
11.
СТРУКТУРА ЦИФРОВОГО КАНАЛАСВЯЗИ
Сообщение
(вх)
П-1
АЦП
Кодер
источника
Кодер
канала
Помехи
Модулятор
ЦАП
Линия
связи
Интерполятор
Демод
улятор
П+1
Декодер
Сообщение
(вых)
12.
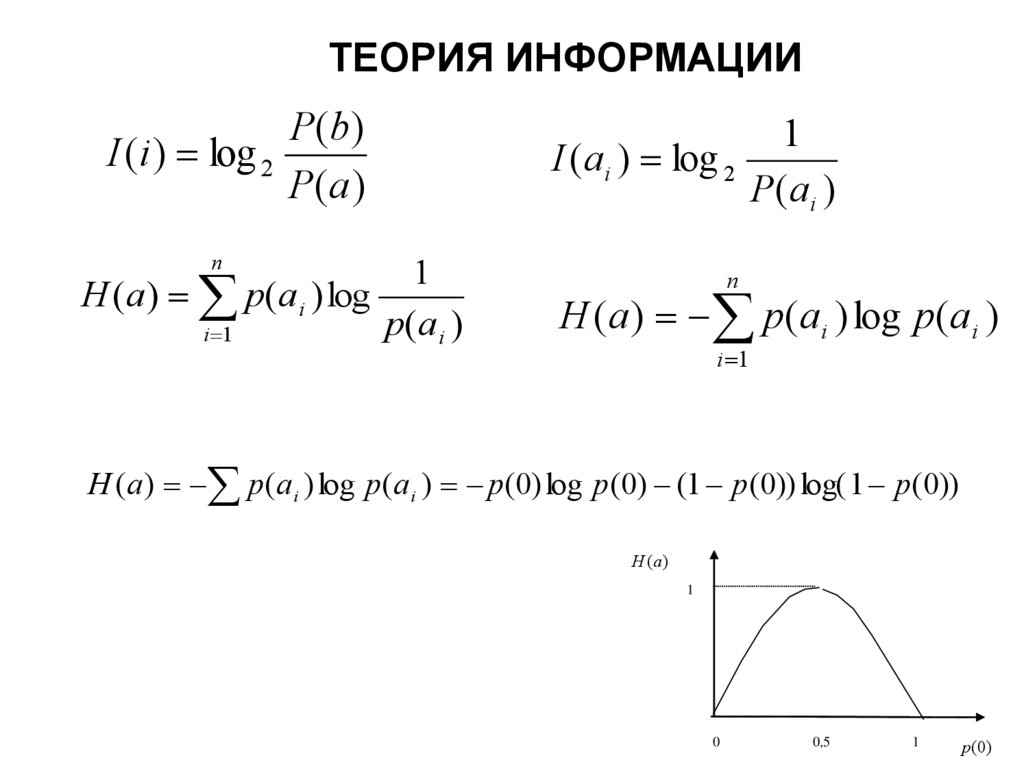
ТЕОРИЯ ИНФОРМАЦИИP ( b)
I (i ) log 2
P( a )
1
I ( ai ) log 2
P ( ai )
n
1
H (a ) p(ai ) log
p( a i )
i 1
n
H ( a ) p( a i ) log p( a i )
i 1
H ( a ) p( a i ) log p( a i ) p(0) log p(0) (1 p(0)) log( 1 p(0))
H (a )
1
0
0,5
1
p (0)
13.
Третье свойство энтропии это теорема сложения энтропийn
m
H ( x, y ) p( x i , y j ) log p( x i , y j )
I ( x i , y j ) log p( x i , y j )
i 1 j 1
H ( x, y ) H ( x ) H ( y )
p( x i , y j ) p( x i ) p( y j / x i ) p( y j ) p( x i / y j )
H ( x, y ) p( xi , y j ) log p xi , y j p( x i ) p( y j / x i )[log p( xi ) log p( y j / x i )]
n
m
n
i 1 j 1
m
i 1 j 1
n
m
n
m
i 1
j 1
i 1
j 1
p( x i ) log p( x i ) p( y j / x i ) p( x i ) p( y j / x i ) log p( y j / x i )
H ( x, y ) H ( x ) H ( y / x )
14.
Односвязная цепь Марковаxj
xi
t
I ( x i / x j ) log p( x i / x j )
n
n
j 1
i 1
n
H ( x / x j ) p( x i / x j ) log p( x i / x j )
i 1
p( x i / x j ) p( x i )
H ( x ) 2 p( x j ) p( x i / x j ) log p( x i / x j )
H ( x) 2 H ( x)
H ( x ) max H ( x )
R
H ( x ) max
H ( x ) ср H ( x ) / ср
15.
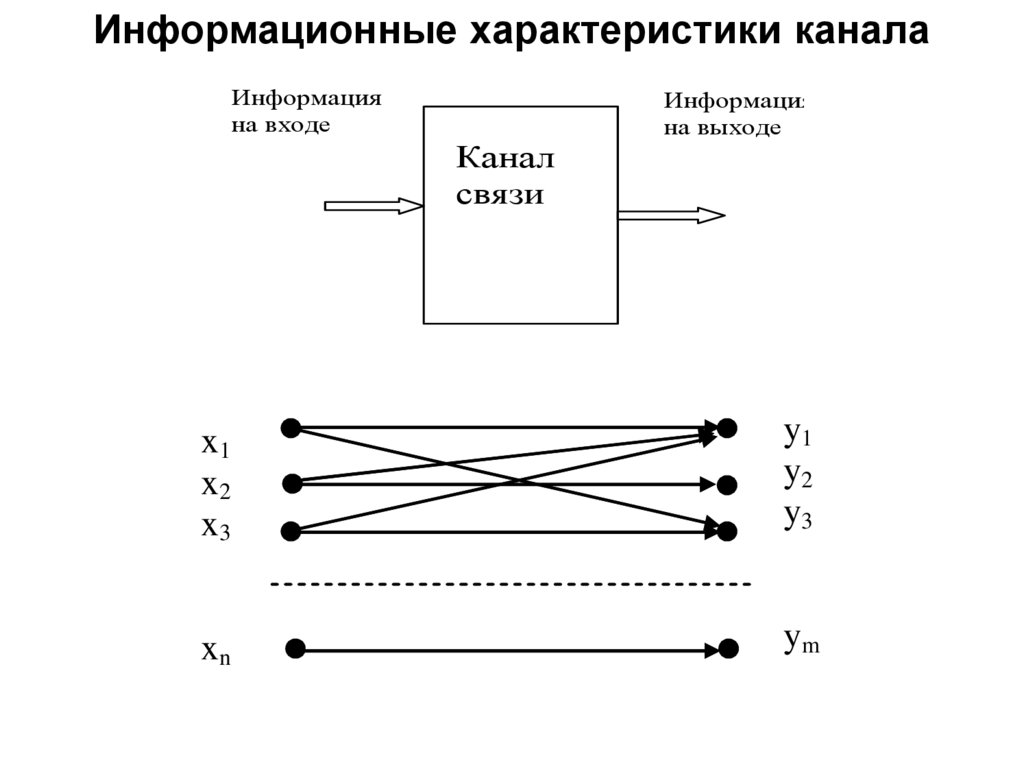
Информационные характеристики каналаИнформация
на входе
Канал
связи
Информация
на выходе
x1
x2
x3
y1
y2
y3
xn
ym
16.
p /( m 1) при i j,p ( y j / xi )
1 p при i j.
Симметричный канал
1-p
0
0
p
p
1
1
1-p
1-p
0
0
?
p
p
1
1
1-p
17.
p( x1 / y1 ) p ( x1 / y2 ) ... p ( x1 / ym )M
p( x2 / y1 ) p ( x2 / y2 ) ... p( x2 / ym )
.....................................................
p( xn / y1 ) p( xn / y2 ) ... p ( xn / ym )
n
m
p( x
i 1 j 1
i
/ y j ) 1
18.
Для аналоговых каналовz (t ) ku(t ) (t )
H (u ) p(u i ) log p(u i )
n
ср i p(ui )
i 1
Количество информации, передаваемое по каналу
в единицу времени называется скоростью передачи информации
R H (u ) / ср
R
19.
C max1
H (u )
ср
0
Сообщения
X1
X2
X3
X4
Сигналы
U1
U2
U3
Резерв по времени
U4
бит
с
20.
nn
i 1
i 1
ср i p( x i ) 0 n i p( x i )
n
R
H (u )
ср
P( x i ) log P( x i )
i 1
ср
n
P( x i ) log P( x i )
i 1
0 n i P( x i )
max H ( x ) 1
C
min ср
0
ni log P( xi )
21.
Алгоритм статистического кодирования ХафменаСообщен
ие x i
P( x i )
x3
0.6
0.15
0.13
0.12
x2
x1
x4
Вспомогательные столбцы
1
2
3
0.6
0.6
1
0.25
0.4
0.15
Сумма
Сумма
Код
1
00
110
010
1
0.6/1
0.4/0
x3
0.15/0
0.25/1
0.12/0
x4
x2
0.13/1
x1
22.
Пропускная способность канала с помехамиI ( xi , y j ) log
p( xi / y j )
p( xi )
H ( x, y) p( xi , y j ) log
i
j
p( xi / y j )
p( xi )
.
p( xi , y j ) p( xi ) p( y j / xi ) p( y j ) p( xi / y j ),
H ( x, y) p( y j ) p( xi / y j ) log p( xi / y j ) p( xi ) log p( xi ) p( y j / xi ).
j
i
i
j
23.
H ( x, y ) H ( x ) H ( x / y ) H ( x, y ) H ( y ) H ( y / x )H ( x / y ) p( y j ) p( xi / y j ) log p( xi / y j ).
j
i
H ( x, y )
R
tср
24.
CH ( x) H ( x / y)
H ( x) мах 1
C
1
1
( H ( x ) H ( x / y ))
(1 H ( x / y )).
H ( x / y) p( y j ) p( xi / y j ) log 2 p( xi / y j )
j
C
1
(1 p0 log 2 ( p 0 (1 p0 )) log( 1 p0 )).
25.
Теорема Шеннона для канала с помехамиПусть H (a ) производительность источника,
тогда, если производительность источника
меньше пропускной способности канала
H (a) C
то можно передавать сообщения со сколь угодно
высокой достоверностью
r
k
n
26.
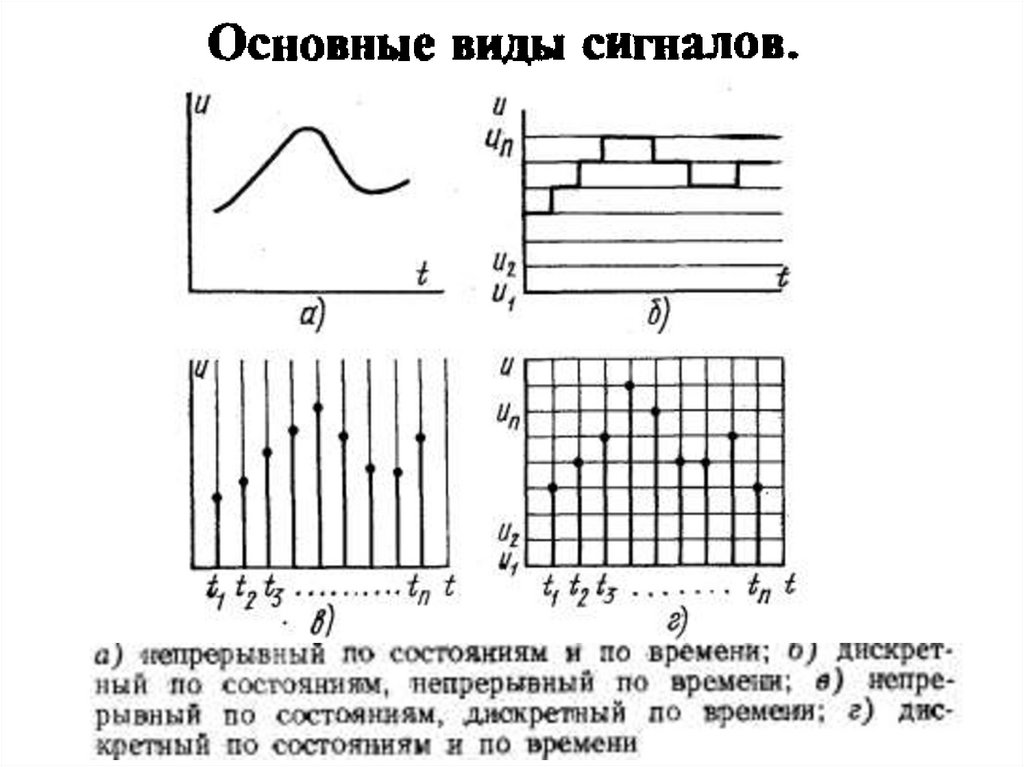
Классификация сигналовСигналы
регулярные
случайные
одиночные
периодические
тестовые
Гармонический сигнал
Ступенчатая функция
U(t)
U(t)
t
= 2* *f0
1 t 0
U( t )
0 t 0
Дельта функция Дирака
t 0
U(t ) ( t )
0 t 0
U(t)
t
U(t) = A sin( 0t)
t
27.
Регулярные сигналы (детерминированные)и их спектры
• Периодические сигналы
U(t)
0
t1
t2
T
Рис.5 Периодический сигнал
U(t) a i Ψ i (t)
i 0
t
at, 0 t t 1 ;
U(t) b at, t 1 t t 2 ;
0, t t T.
2
28. Свойство ортогональности
C , i k ;k
(
t
)
*
(
t
)
dt
k
0 i
0, i k
T
(3)
1, i k ;
0 1 (t ) k (t )dt 0, i k.
Ψn(t)
n(t)
.
Cn
T
T
T
0
0
(4)
S (t ) bn n(t )
(5)
n 0
T
bn n ( t ) ( t )dt bn n ( t ) k ( t )dt
S( t ) k ( t )dt n
k
n
(6)
0
0
0
||
1
T
b
k
S( t ) k (t )dt
.
0
(7)
29. Ряд Фурье
Первая формаa0
S( t )
An cos[ n 1 t n ]
2 n 1
(10)
Вторая форма ряда
a0
S (t ) (an cos 1t bn sin 1t )
2 n 1
Коэффициенты ряда
T
a0 1 T
2
S(t )dt an
S( t ) cos 1 tdt
2 T0
T0
.
(11)
T
2
bn S( t ) sin 1 tdt
T0
Третья форма ряда
1
j ( n .1t )
S (t ) An`e
2 n
(15)
e jx cos( x) j sin( x)
30. Свойства ряда Фурье
Ank( )
огибающая
спектра амплитуд
a0
2
1 2 1 3 1 4 1 5 1
n
огибающая
спектра фаз
1
2 1
3 1
Рис. 8 Характеристика гребенчатого фильтра
-
Рис. 7 Дискретные спектры
гипотетического периодического сигнала
0 0
0
S(t) - чётная S(t) - нечётная
S(t) – ни чётная,
ни нечётная
Рис. 9 Выбор начала отсчета сигнала
31. Средняя мощность периодического сигнала
T1 2
P S ( t )dt
ср T
0
(18)
1
1 a0
2
P S (t)dt [
Ancos(nω1 t n) ] 2 dt
ср
T0
T 0 2 n 1
T
2
T
2
1 a0 2 a0
1
An cos( n 1t n) dt An cos( n 1t n) dt
T 0 2 T 0 2 n 1
T 0 n 1
T
T
T
2
1 a0
P0
T 0 2
T
T
2
1
A
2
2
Pср A cos ( t )dt
T0
2
Pср P0 Pn
n 1
1 2
Pn A n
2 n 1
n 1
«равенство
Парсеваля»
32. Практическая ширина спектра периодического сигнала
Искажения сигнала при ограничении спектраСвязь искажений сигнала
с его частотным составом
Исходный сигнал
1-й член ряда
Искаженный сигнал
t’0 – время задержки
t0 срабатывания устройства
3-й член ряда
Сумма гармоник
5-й член ряда
Сумма гармоник
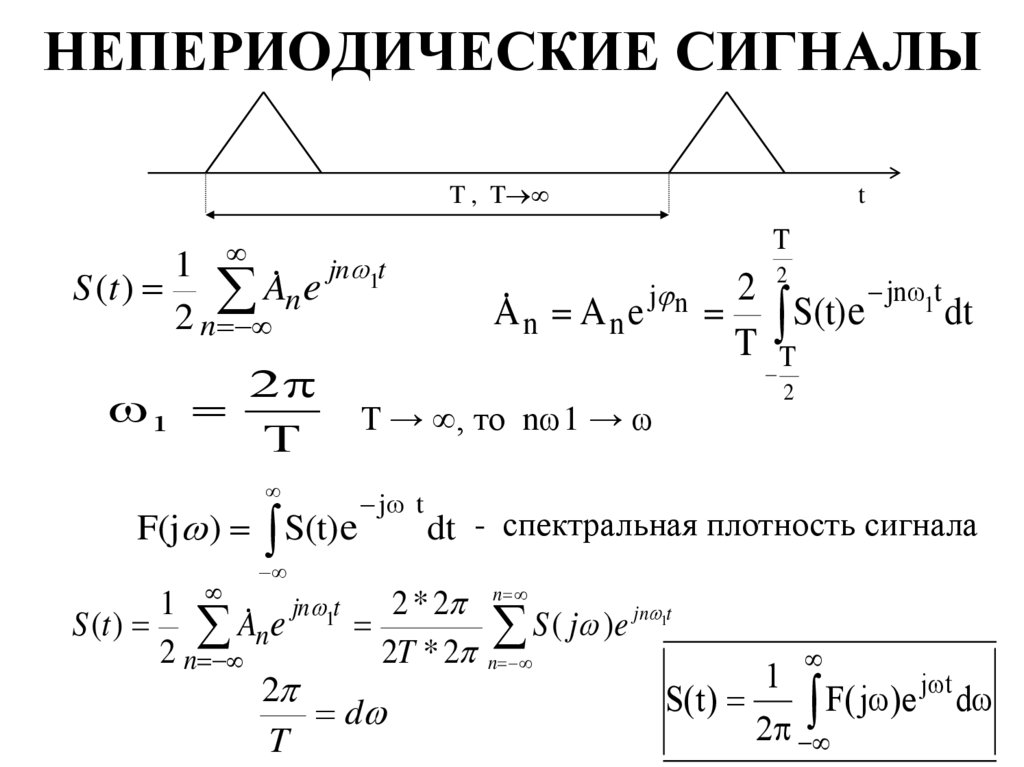
33. НЕПЕРИОДИЧЕСКИЕ СИГНАЛЫ
T , Tt
T
1
jn t
S (t ) A n e 1
2 n
1
2
T
F(j ) S(t) e
A n A n e j n
2 2
jnω1t
S(t) e
dt
T T
T → , то n 1 →
jω t
2
dt - спектральная плотность сигнала
1 jn 1t
2 * 2
S (t ) An e
2 n
2T * 2
2
d
T
n
jn 1t
S
(
j
)
e
n
1
j t
S( t )
F
(
j
)
e
d
2
34. Свойства спектральной плотности
а)F ( j ) F ( )e
в)
j ( )
F( j ) S( t )e j t dt S( t ) cos ( t )dt j S( t ) sin ( t )dt
б) Модуль спектральной плотности
F( )
a ( )
b ( )
b( )
F( ) a ( ) b ( ) ( ) arctg
a ( )
2
2
г) S(t) = S1(t) + S2(t), F(j ) = F1(j ) + F2(j ).
0
Фаза спектральной плотности
д) S1(t - t1) S(t) F(j ) S1(t) F( j )e j t 0
S(t)
( )
0
t1 t
е)
dS( t )
S1 ( t )
dt
S1 ( t ) S1 ( t )dt
0
S(t-t1)
t
F1 ( j ) j F( j )
F( j )
F1 ( j )
j
35. Спектральная плотность прямоугольного импульса
U(t)F( j )
1
t
0
j t
j t
U
(
t
)
e
dt
e
dt
1 j t
e
j
0
1* 1
1*
1* 2
2 2 2
1 2
1
1 cos( ) j sin( ) j cos( ) 1 j sin( )
j
ωτ
sin
2
F(ω( 1* τ
ωτ
2
F( )
1
1 e j
j
cos( ) - 1
( ) arctg(
)
sin( )
36. Энергия одиночного сигнала
W S ( t )dtF( j )
2
F( j )F( j )d F( j ) S(t )e
j t
S(t )e
j t
dt
F( j )
j t
S
(
t
)
e
dt
j t
dtd S( t ) F( j )e d dt 2 S 2 ( t )dt 2 W
2 S( t )
Равенство Парсеваля
1
2
W
F ( )d
2
2
2
В
В
*с
В
2
F( ) F ( ) 2
Гц
Гц
Гц
37. Практическая ширина спектра одиночного сигнала
Полоса частот сигнала от 0 до .Зависимость энергии
сигнала от границы спектра
Процент от полной энергии сигнала W
W'
гр
1
2
W'
F ( )d
2
Полная энергия сигнала
W
гр
ωгр
0
с
38. ПРЕОБРАЗОВАНИЕ СИГНАЛОВ В ЦИФРОВЫХ СИСТЕМАХ СВЯЗИ
U1ПРЕОБРАЗОВАНИЕ СИГНАЛОВ В
ЦИФРОВЫХ СИСТЕМАХ СВЯЗИ
Выборка сигналов.
U(t)
U6
U5
U3
U4
U1
U2
t1
t2
t3
t4
t5
t6
t
39. Дельта функция Дирака.
δ(t)
0
t
t
δ(t)dt
1
t 0
( t )
0 t 0
2 t
3 t
4 t
t
Дискретизирующая последовательность
η(t)
k
δ(t k t)
k
U k (t)
n
U(t)k (t k t)dt
0
40. Получение выборки
U(t)ИМ
Uk(t)
(t)
Шаг выборки
1
Δt
2Fc
fд 2Fc
t
Теорема отсчетов для синусоиды
41. Восстановления сигнала
sin 2 Fc ( t n t )S( t ) a n n ( t ) S(n t )
2 F ( t n t )
n 0
n a
c
n
sinx
x
n ( t )
1
0
Функция отсчётов при n=0
t
42. Свойство функции отсчетов
t = n t→
sinx
1
x
→
t = (n + 1)
sin2 Fc((n+1)t-n t)= sin2 Fc t = sin = 0
1
1 f 2F 2 t
Fс
д
c
f
2
д
43.
U(t)S(t)
2
t
t
1-й член ряда
t
1-й член ряда
2-й член ряда
t
t
Сумма членов
2-й член ряда
t
Ряд Котельникова
t
Представление прямоугольного
сигнала рядом Котельникова
44. Интерполяция
1-й метод интерполяция полиномомS( t )
N
ant
n
2-й метод Сплайн интерполяция
1. Cтупенчатая интерполяция сплайном
S(t)
N = 0, S(t) = а0
n
0
S(t)
t
N t
Задержка сигнала при интерполяции
2. Линейная интерполяция сплайнами
S(t)
t
t
3. Квадратичная интерполяция сплайнами
N = 2, то S(t) = а0 + а1t + а2t2
S(t)
N = 1, то S(t) = а0 + а1t.
t
t
45.
3-й метод Интерполяция ФНЧИзмерение импульсной характеристики ФНЧ
1
K ( )
1 12 n
(t)
1
ср
K( )
ФНЧ
ср
или S(n t)
g(t)
или S’(t)
g(t)
n=5
n=1
tз
ср
ср – частота, при которой наблюдается
резкий спад коэффициента передачи.
t
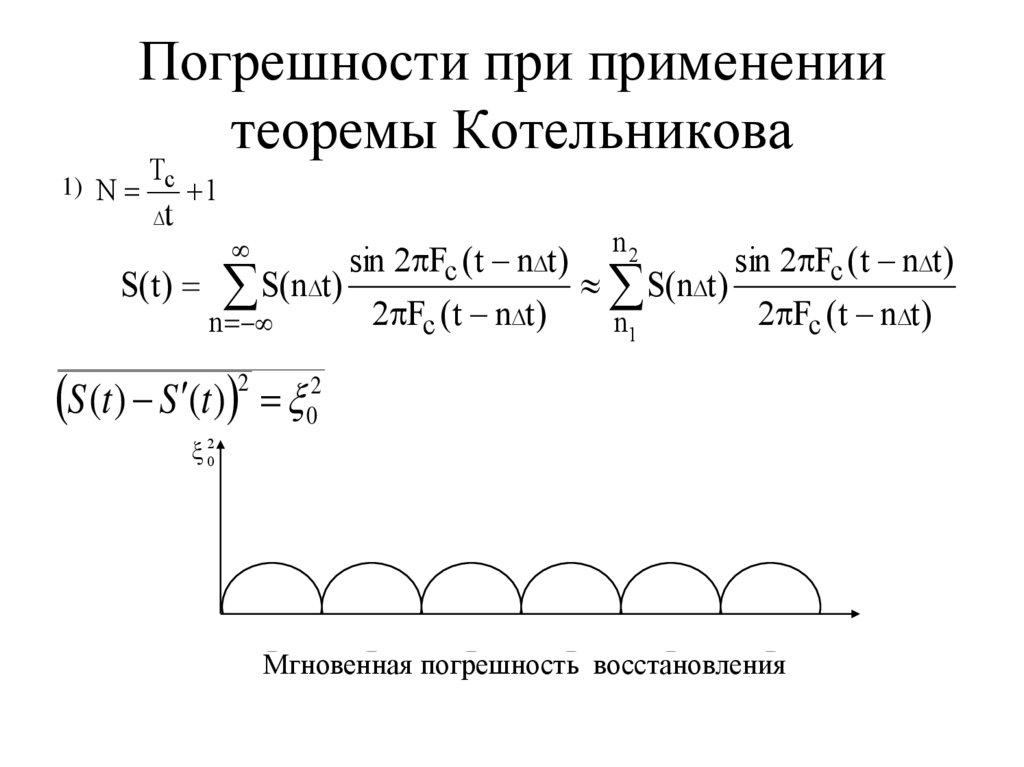
46. Погрешности при применении теоремы Котельникова
1)N
Tc
t
1
n
2
sin 2 Fc ( t n t )
sin 2 Fc ( t n t )
S( t ) S(n t )
S(n t )
2 Fc ( t n t )
2 Fc ( t n t )
n
n1
S (t ) S (t )
2
02
02
Мгновенная погрешность восстановления
47.
2) Эта причина погрешности заключается в ограничении спектра сигнала величиной Fc,t t , тем меньше данная погрешность
тогда как теоретически спектр бесконечен. Чем меньше
3) причина погрешности заключается в не идеальности интерполятора,
в частности не идеальности фильтра низкой частоты, ФНЧ
идеальный ФНЧ
К )
Реальный ФНЧ
ср
Модуль характеристики передачи ФНЧ
( )
Реальный ФНЧ
Идеальный ФНЧ
ср
Фазовая характеристика ФНЧ
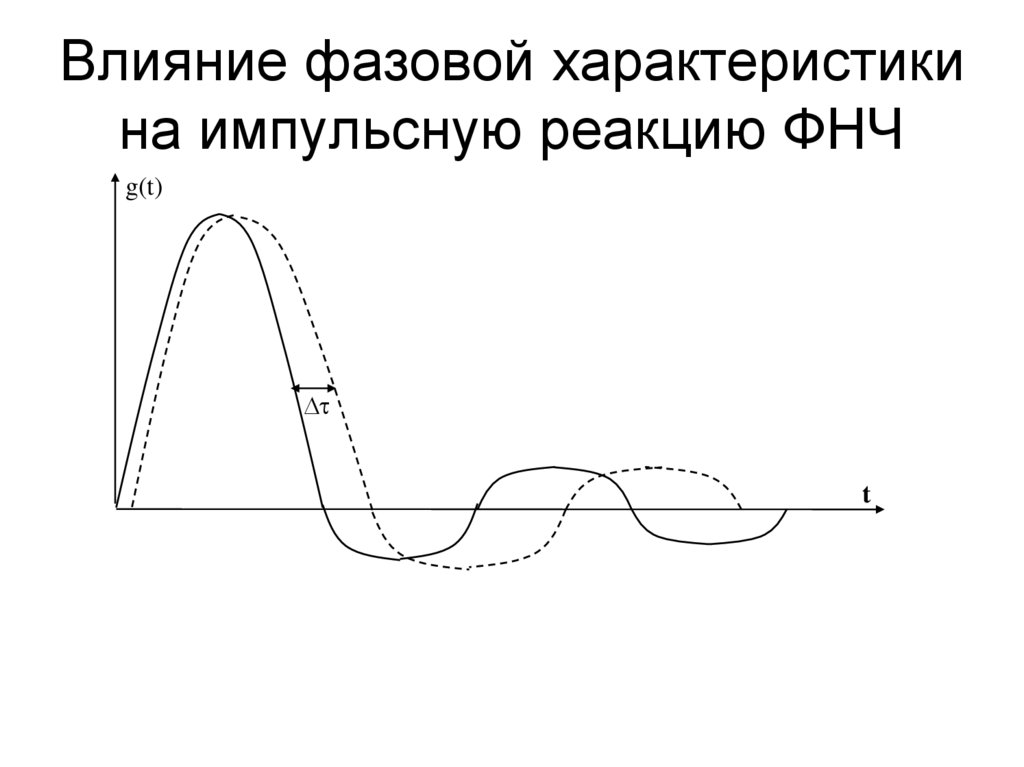
48. Влияние фазовой характеристики на импульсную реакцию ФНЧ
g(t)t
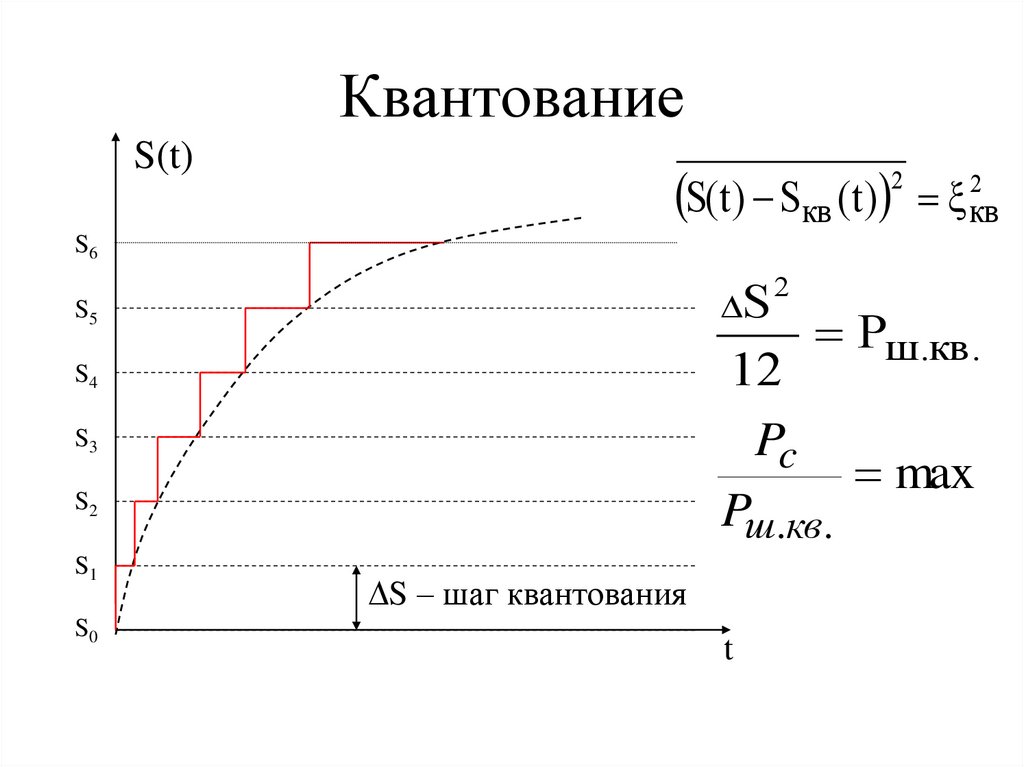
49. Квантование
S(t)S(t) Sкв (t)
2
кв
2
S6
S
S5
S3
S2
S0
Pш.кв.
12
Pc
max
Pш.кв.
S4
S1
2
S – шаг квантования
t
50. Импульсно – кодовая модуляция (ИКМ)
mN 2
S(t)
t
S
кодер
Преимущества такой передачи.
1. Хорошая согласованность со средствами связи и вычислительной техники.
2. При передаче на большие расстояния возможна регенерация цифрового сигнала
(осуществляется в регенераторах).
3. Мы передаём только 0 и 1,поэтому передатчик работает в пиковом режиме
и вероятность ошибки уменьшается.
4. Возможно, защититься от помех помехоустойчивым кодом.
Недостатки.
Для передачи требуется более широкая полоса частот. Например для канала тональной
частоты, имеющего полосу 300 ÷ 3400 Гц, требуемая частота дискретизации
fд 2Fc, fд 8кГц. При кодировании 8-и разрядным кодом
основная частота следования кодовых импульсов будет 64кГц.
51. Формирование ИКМ сигнала
Каждый сегмент разбиваетсяна 16 квант (уровней)
8 сегмент
Р1
Р2
Р3
Р4
Р5
Р6
Р7
7 сегмент
6 сегмент
Полярность
импульса
5 сегмент
4 сегмент
3 сегмент
2 сегмент
1 сегмент
Номер
сегмента
Номер кванта
Р8
52. СЛУЧАЙНЫЕ СИГНАЛЫ
Получение выборки непрерывногосигнала
p(x1)+p(x2)+…+p(xm) = 1
Непрерывный случайный
сигнал
запуск
Генераторы
случайных
сигналов
x(t)
x(t)
Регистратор
{xi}
АЦП
{xi}
[xmin;xmax]
x
ni
t
pi*
ni
N
53.
Таблица 1. Статистические данные сигнала.интервалы
xmin – x2
x2 – x3
x3 – x4
число
попаданий
n1
n2
n3
p *i
*
p *2
p *3
p1
и
т.д.
x dx
p *i
Гистограмма сигнала
p *i
x
dp
p *i
xmin x2
x3
x4
x5
x
x
pi* dp
lim x dx W ( x)
x dx
54.
Закон распределения плотности(дифференциальный закон)
Интегральный закон распределения
W(x)
F( x )
x
W(x)dx
dp
dx dx dp p p(x X пор )
x2
x W(x)dx p(x
1
x x2)
1
p(x1 x x 2 ) F(x 2 ) F(x1 )
x
Числовые характеристики сигналов – моменты
n
n 1 x 1 n 2 x 2 ... n 1
n2
mx
x1
x 2 ... p( x i ) x i
N
N
N
i 1
p(x) = W(x)dx
mx
xW ( x )dx
55.
x i m xs
n
s x i m x p( x i )
s
i 1
x m x
s
S=2
s
x m x
s
W( x )dx
n
D x x i m x p(x i )
2
i 1
Dx
x m x W(x)dx
2
56.
Законы распределения сигналовW(x),
W(y)
W(x)
W(y)
my
mx
x
y
57.
Система случайных сигналовдифференциальный закон (плотности);
W(x1 , x 2 ,..., x n )
сигнал – x1
Приёмник
интегральный закон.
F(x1 , x 2 ,..., x n )
помеха – x2
многомерный дифференциальный
закон распределения,
W(x1 , x 2 ,..., x n )
F( x 1 , x 2 ,..., x n )
x1 x 2
xn
... W(x , x
1
2
,..., x n )dx 1 , dx 2 ,..., dx n
n
d F( x 1 , x 2 ,..., x n )
W( x 1 , x 2 ,..., x n )
dx 1 , dx 2 ,..., dx n
58.
Числовые константы, моменты первого порядкаs = 1,
=0
или
s = 0, = 1
W(x,y)=W(x)W(y/x)=W(y)W(x/y) - для зависимых сигналов
W(x,y)=W(x)W(y) – для независимых сигналов
1,0
W ( y) dxdy xW ( x ) W ( y / x )dydx xW ( x )dx m x
xW (x ) или
или
W(y / x)
W ( y)
||
1
Момент второго порядка при s=0, и =1 или s=1, =1
2, 0
2
(
x
m
)
x W( x, y)dxdy D x
59.
Двумерный закон системы сигналовW(x,y)
y
my
mx
x
60.
Центральный момент второго порядка при s=1, =1K xy
(x m x )( y m y )W(x, y)dxdy
K xy ( x i m x )( y j m y )p( x i , y j )
i
j
W(x,y) = W(x)W(y)
K xy
( x m x ) W ( x )dx ( y m y ) W ( y)dy
m x m x 0
K xy
(x m x )
2
W(x)
W ( y)dydx
||
1
Dx Dy
61.
Коэффициент корреляцииrxy
rxy 0
K xy
Dx Dy
1 rxy 1
- статистической связи между сигналами нет
rxy 1 предельный случай
статистической связи – функциональная связь
rxy 1
- положительная статистическая связь
(увеличение одного сигнала вызывает увеличение другого сигнала.)
rxy 1
- отрицательная статистическая связь
(увеличение одного сигнала вызывает уменьшение другого сигнала
62.
Статистические связи между сигналамиx
50 Гц
rxy
- статистическая
связь есть
0,9
150 Гц
x
50 Гц
rxy 0,1
- статистической
связи нет
200 Гц
y
63.
Сигнал как случайный процессx(t)
x1(t)
x2(t)
x3(t)
t1
{xi}
Случайные функции сигнала
W(x,t1) F(x,t1)
mx(t1), Dx(t1)
xW (x, t )dx
m x (t 1 )
D x (t 1 )
1
x
t1
x m x (t ) W(x, t )dx
2
1
y
t
t1
t2
1
t1
t2
t
64.
m x (t ) m y (t)D x (t) D y (t)
и
для каждого момента времени t1 и t2 есть множество {xi} и {yj}
W(x1,x2; t1,t2)
K x (t 1 , t 2 )
x
1
m x (t 1 ) x 2 m x (t 2 ) W(x 1 , x 2 ; t 1 , t 2 )dx 1dx 2
K y (t 1 , t 2 )
y
1
m y (t 1 ) y 2 m y (t 2 ) W( y1 , y 2 ; t 1 , t 2 )dy1dy 2
Корреляционный момент является функцией времени
и называется функцией корреляции
или функцией автокорреляции (АКФ).
K y ( t 1 , t 2 ) < K x (t 1 , t 2 )
65.
Cвойства автокорреляционной функции (АКФ)Допустим t1 = t2, тогда:
K y (t 1 , t 1 )
y
2
1 m y ( t 1 ) W( y1 , t 1 ) W( y 2 , t 1 )dy1dy 2
y
2
1
m y ( t 1 ) W ( y1 , t 1 )dy1
W( y
2
, t 1 )dy 2 D y
.
||
1
При t1 = t2 АКФ принимает максимальное значение,
равное дисперсии сигнала.
Функция АКФ носит чаще всего убывающий характер,
так как статистическая связь
с увеличением временного интервала разрушается.
66.
Введём нормированную функцию АКФ:K x (t 1 , t 2 )
rx ( t 1 , t 2 )
Dx
1 rx (t 1 , t 2 ) 1
67.
Cтационарный сигналx
t
x
x1
x2
t
x3
68.
Его характеристики mx и Dx не зависят от времени, например,Dx
2
(
x
m
)
x W( x )dx
АКФ является функцией разности = t2 - t1 , Kx( ):
K x ( )
x
1
m x x 2 m x W( x 1 , x 2 , )dx 1dx 2
69.
Свойство эргодичностиK1
K2
x1(t)
x2(t)
помехи
каналы
Kn
xn(t)
70.
xx1
x2
t
x3
В этом случае свойство эргодичности отсутствует
x
x2
x1
x3
t
В этом случае свойство эргодичности присутствует
71.
Сигналы конечной длительности ТМатематическое ожидания
T
1
m x lim x ( t )dt
T T 0
Дисперсия
T
1
2
D x lim x ( t ) m x dt
T T 0
Автокорреляционная функция (АКФ)
T
1
K ( ) lim x ( t ) m x ( x ( t ) m x )dt
T T 0
Если m x 0, то
T
1
K ( ) lim x ( t ) x ( t )dt
T T 0
при = 0, то
K( ) D x
Нормированная АКФ
K ( )
r ( )
Dx
от –1 до +1
72.
Свойства АКФ1) При = 0 АКФ принимает максимальное значение,
так как корреляционные связи в этом случае максимальны,
и равна дисперсии (при ненормированной функции)
или единицы (при нормированной функции).
2) АКФ четная функция . Это временной сдвиг и
безразлично в какую сторону он будет сделан,
K x ( ) K x ( )
3) АКФ чаще всего уменьшается с увеличением ,
так как убывают статистические связи между
случайным сигналом в его сечениях. Однако,
если в сигнале есть какая- то периодичность,
этот принцип может нарушаться.
Корреляционные связи будут расти через интервал
равный периоду и АКФ возрастет.
73.
Характер убывания АКФK( )
Dx
у случайного сигнала есть
скрытая периодичность
0
T
Регистр сдвига
T1
fT
T2
T3
T4
Uвых
случайного
сигнала
74.
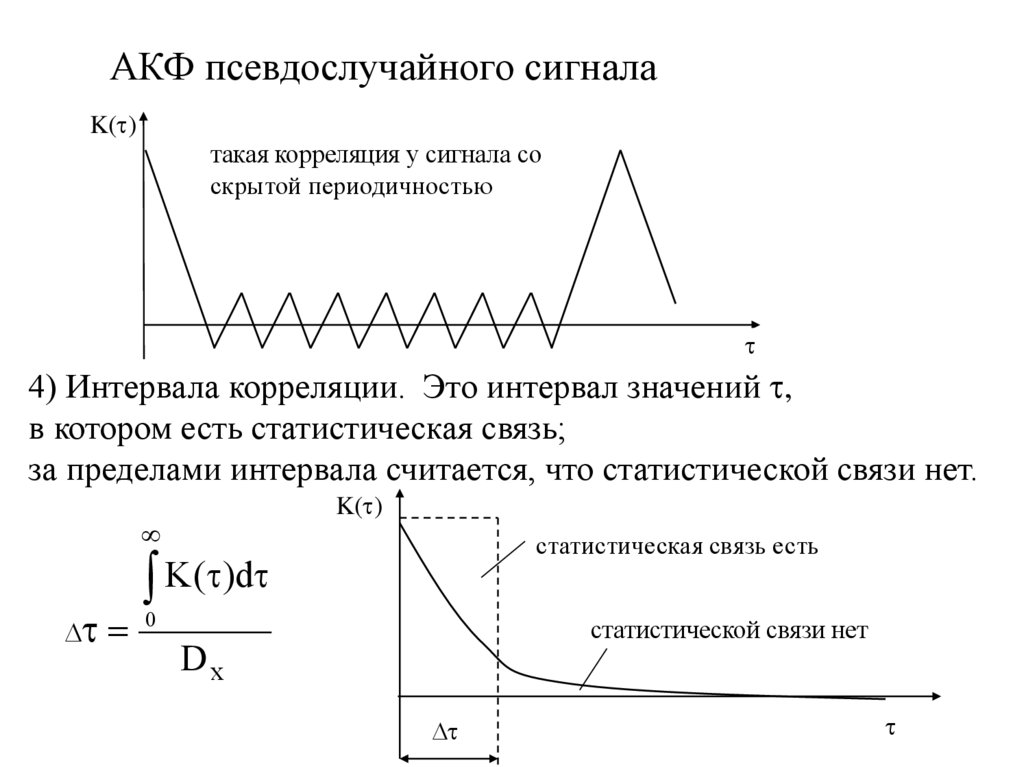
АКФ псевдослучайного сигналаK( )
такая корреляция у сигнала со
скрытой периодичностью
4) Интервала корреляции. Это интервал значений ,
в котором есть статистическая связь;
за пределами интервала считается, что статистической связи нет.
K( )
статистическая связь есть
K ( )d
0
статистической связи нет
Dx
75.
АКФ некоторых случайных сигналов1) Гауссовский случайный сигнал - это непрерывная
функция времени имеющая ширину спектра f.
r( ) e
4 f
2) Речь - функция АКФ имеет колебательный характер
r( ) e
где
= 1000 Гц;
| |
cos(2 f1 )
f1 = 400 Гц.
76.
СПЕКТР СЛУЧАЙНОГО СИГНАЛАt
Т
спектральные плотности S1(jω), S2(jω)
плотность распределения спектра W( ) и
усреднить квадрат модуля спектральной плотности M[S2(ω)]т
Нормируем его по времени
1
2
lim M [ S ( )]T G ( )
T T
1
j
j
G ( ) k ( )e d k ( )
G( )e d
2
77.
СВОЙСТВА СПЕКТРА СЛУЧАЙНОГО СИГНАЛА1)
G( ) G( )
2) G ( )
3)
0
k ( )cos( )d k ( )sin( )d 2 k ( )cos( )d
k(0) Pс р
1
Pср
G ( )d
2
где
G ( )
d
2
78.
4) Практическая ширина спектра случайного сигналаG ( ) d
G( )
G( )max
0
G ( ) max
5) Нормированная спектральная характеристика
G ( )
g( )
G ( ) max
-1 < g ( ) < 1
79.
Заданы два сигнала X(t) и Y(t)X(t)
k( )
t
kx( )
ky( )
Y(t)
t
x y
G( )
Gy( )
Gx( )
y x
80.
МОДЕЛИ СЛУЧАЙНЫХ СИГНАЛОВГауссовский случайный сигнал
Гладкий случайный сигнал
t
Т
Интеграл вероятности
mu=0
y=u/σ
p(u < u0)=p(y < y0)
81. АКФ
D - дисперсия82. СЛУЧАЙНЫЙ ЦИФРОВОЙ СИГНАЛ
S(t)АЦП
1
0
код
1
1
1
0
1
1
0
P1=0,25
0
1
P3=0,25
0
0
P2=0,25
1
1
P4=0,25
83.
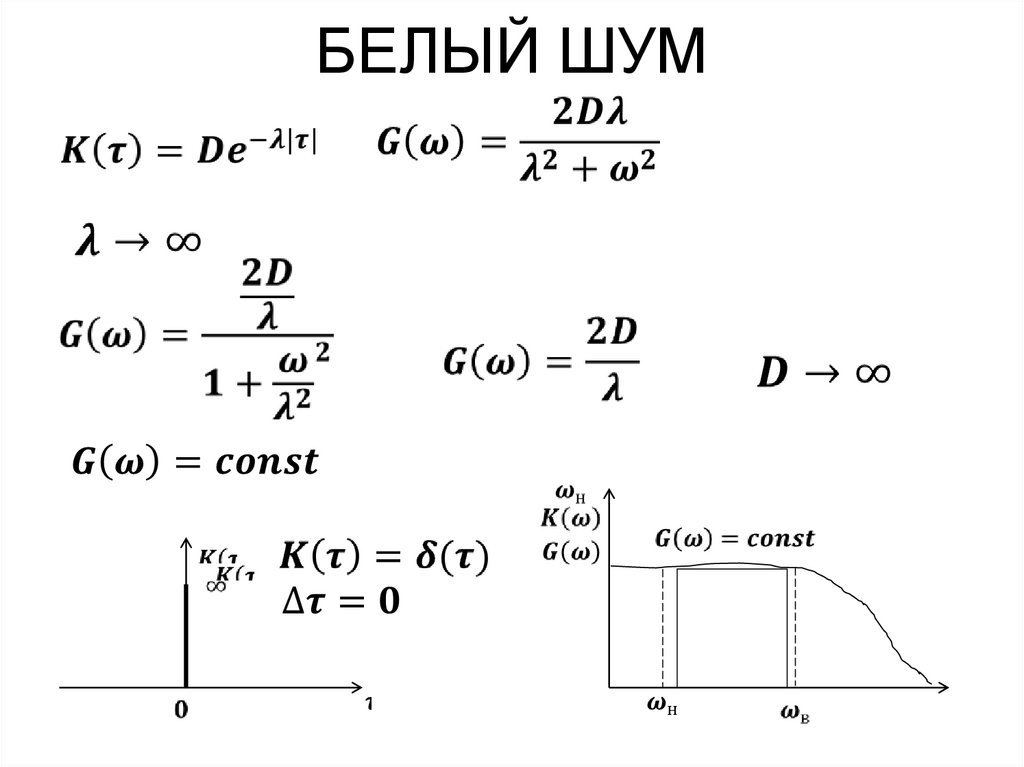
84. БЕЛЫЙ ШУМ
85. УЗКОПОЛОСНЫЙ СИГНАЛ
Белыйшум
К(ω)
S(t)
узкополосный
сигнал
A(t) – случайная амплитуда
φ(t) – случайная фаза
86.
87.
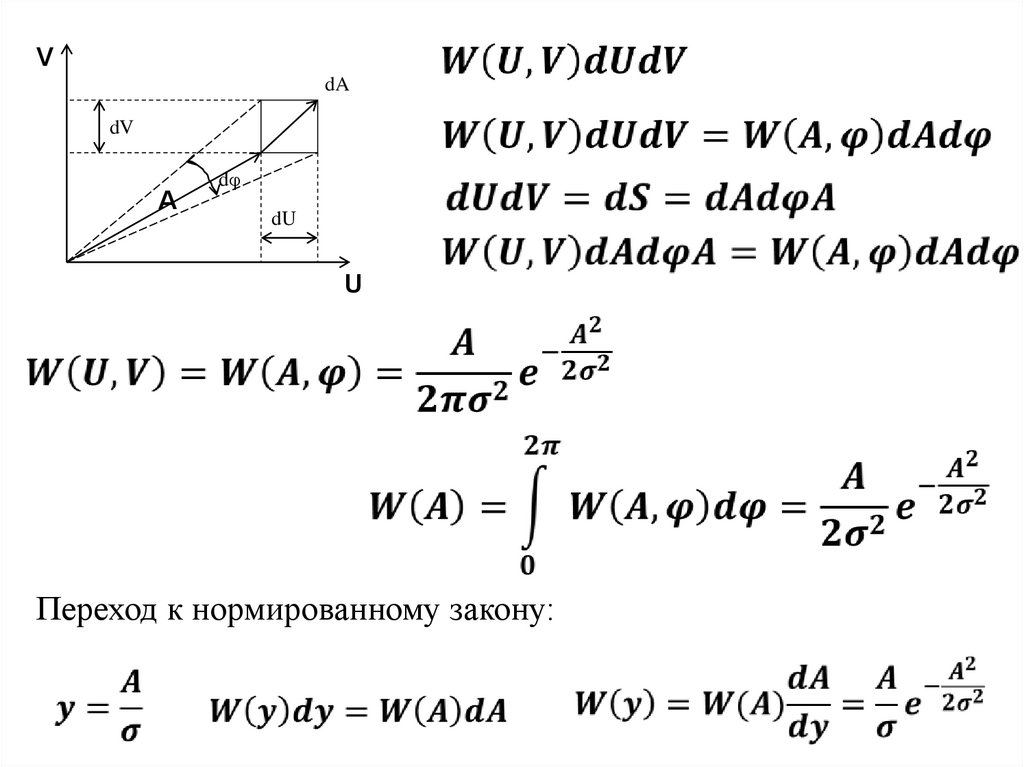
VdA
dV
dφ
A
dU
U
Переход к нормированному закону:
88.
W(y)W(y)
y=1
x
АКФ узкополосного сигнала:
89.
90. Импульсные помехи
А – амплитуда помехиA
t
А0 – амплитуда помехи
91.
- площадь помехиt
Δt
Δt
λ – интенсивность потока помех
m - число импульсов помехи
92. Оптические сигналы
1) Волновая природа света2) Поток частиц
93. Модуляция
1) Импульсная модуляцияu(t)
2) Гармоническая модуляция
A cos 0 t
АМПЛИТУДНАЯ МОДУЛЯЦИЯ (АМ)
При амплитудной модуляции у гармонического сигнала
меняется амплитуда.
A(t ) A0 A u (t )
ЧАСТОТНАЯ МОДУЛЯЦИЯ (ЧМ)
(t ) 0 u(t )
ФАЗОВАЯ МОДУЛЯЦИЯ (ФМ)
(t ) 0 u(t )
вых
несущая
- граничная частота спектра полезного сигнала.
0 - частота несущего сигнала
94. Амплитудная модуляция
tA0
ΔА
t
A0 – средний уровень модифицированного сигнала
S (t ) ( A0 A U (t )) cos 0 t
U (t ) 1cos t
A
m
A0
A
S (t ) ( A0 (1
cos t )) cos 0 t
A0
коэффициент глубины модификации
95.
S (t ) A0 cos 0t A0 m cos t cos 0t;
A0 m
A0 m
A0 cos 0t
cos( 0 )t
cos( 0 )t
2
2
0 A0
0 боковые частоты. m – 0,6 до 0,7;
A0 m
A0
2
A0
A0 m
2
A0 m
2
96.
A0m/2AM
ω0+ λ
ω0 - λ
A0m/2
ω0
Теорема о переносе спектра
A0 При амплитудной модуляции спектр полезного сигнала
переносится в область несущих в виде двух боковых частот,
расположенных симметрично относительно несущих, одна
из них выше, другая ниже.
Энергетические показатели амплитудной модуляции
Pполезнаясоставл
2 Pбок
Pбесполезнаясоставл Pнесущ
2 A02 m 2
A02
2
2
2
m
0
,
7
2
0,25
2
2
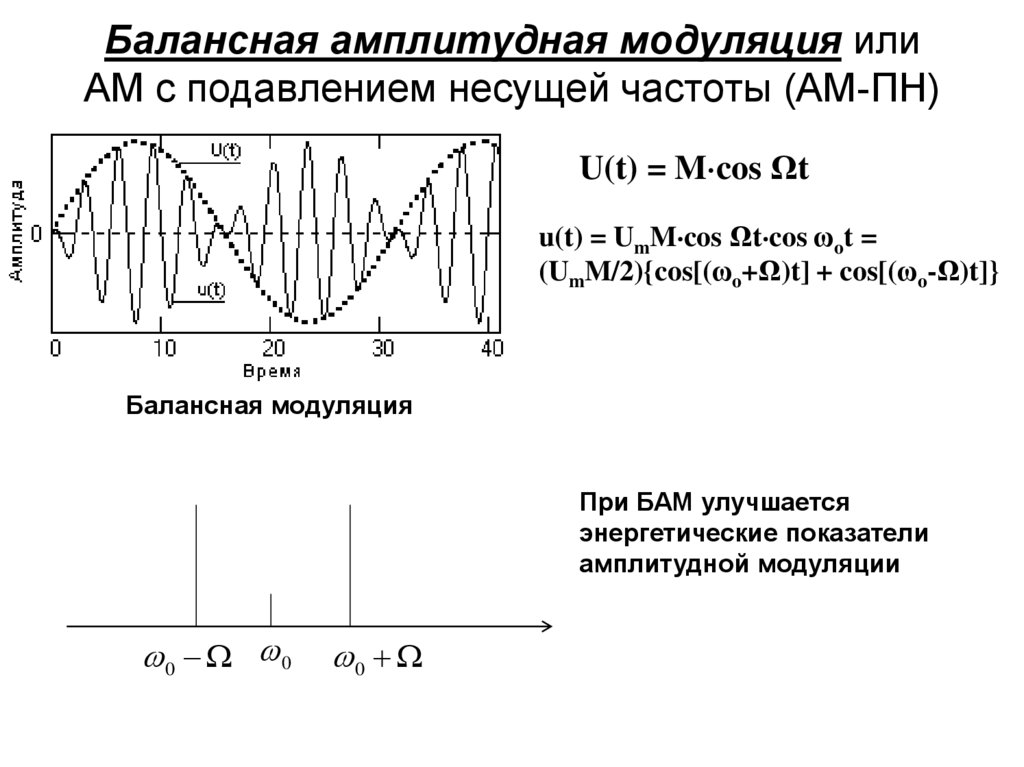
97. Балансная амплитудная модуляция или АМ с подавлением несущей частоты (АМ-ПН)
U(t) = M cos Ωtu(t) = UmM cos Ωt cos ωot =
(UmM/2){cos[(ωo+Ω)t] + cos[(ωo-Ω)t]}
Балансная модуляция
При БАМ улучшается
энергетические показатели
амплитудной модуляции
0 0
0
98. Однополосная амплитудная модуляция.
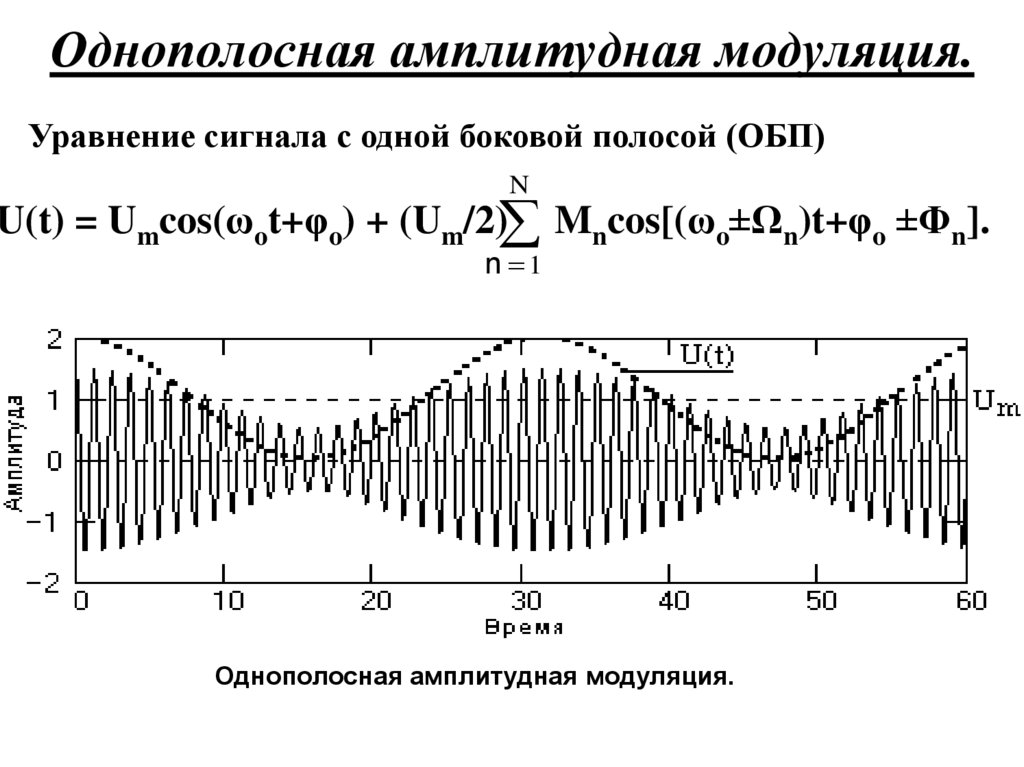
Уравнение сигнала с одной боковой полосой (ОБП)N
U(t) = Umcos(ωot+φo) + (Um/2) Mncos[(ωo±Ωn)t+φo ±Φn].
n 1
Однополосная амплитудная модуляция.
99.
ОБП применяется при построении многоканальныхсистем связи при частотном способе разделения каналов
A0
A0 m
2
Ω
A0 m
2
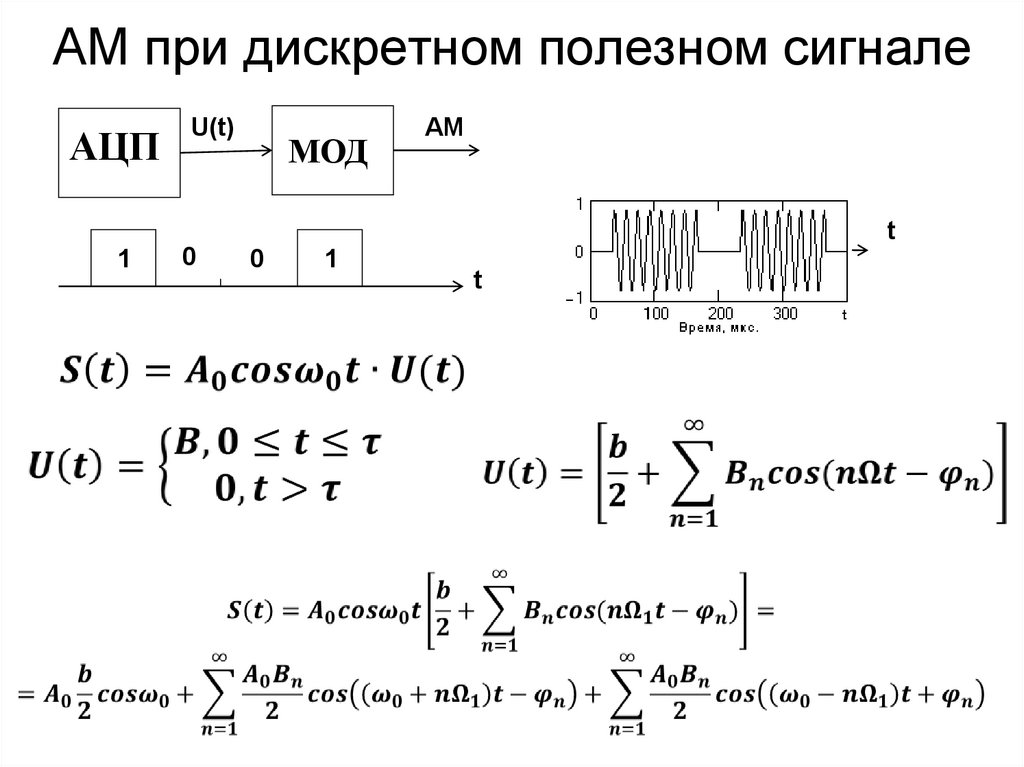
100. АМ при дискретном полезном сигнале
АЦПU(t)
МОД
АМ
t
1
0
0
1
t
101.
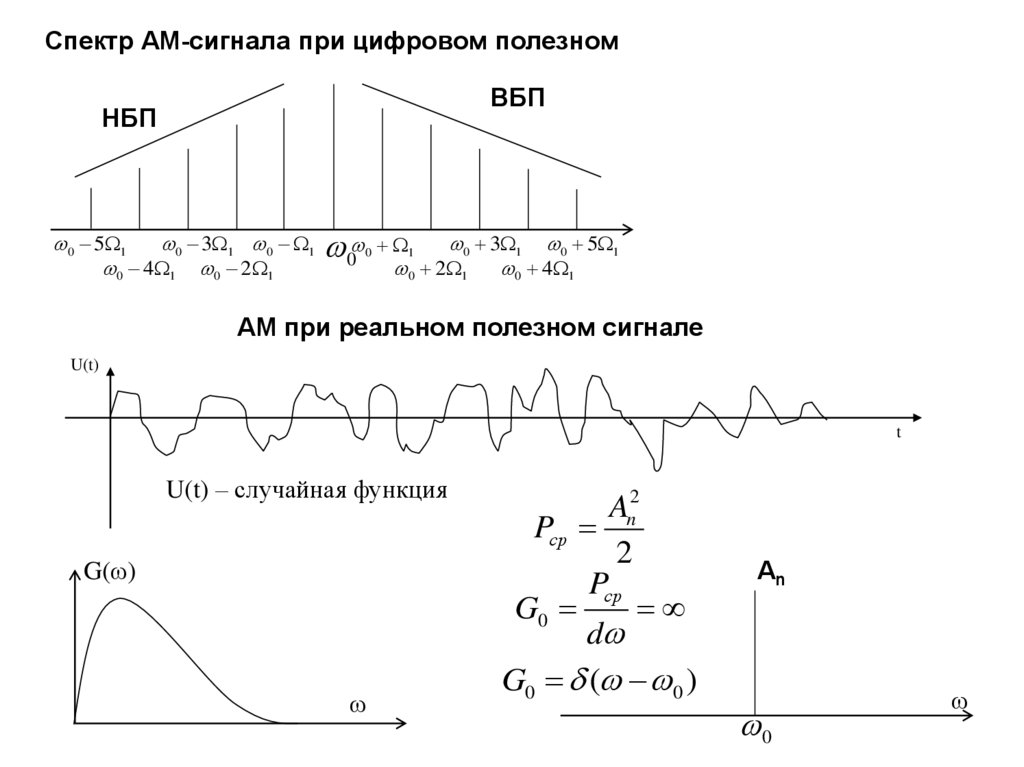
Спектр АМ-сигнала при цифровом полезномВБП
НБП
0 5 1
0 3 1 0 1
0 4 1 0 2 1
0
0
0 3 1 0 5 1
0 2 1 0 4 1
1
АМ при реальном полезном сигнале
U(t)
t
U(t) – случайная функция
G(ω)
ω
An2
Pср
2
Pср
G0
d
G0 ( 0 )
An
0
ω
102.
Спектр мощности несущего сигналаω
Согласно теореме о переносе спектра модулированный сигнал
представляется следующим образом:
G0 ( 0 )
G0 ( 0 )
0
103. Угловые модуляции
104.
Частотная модуляция (ЧМ)105.
Показатели модуляцииΔω
β
Δω
β
Ω
106.
Фазовая модуляция (ФМ)(t ) 0 u(t )
107.
Δφβ
Δω
Δφ
Ω
108. Спектр модулированного по углу сигнала
ЧМ:ФМ:
109.
При110.
Функции Бесселя Jk(x)x – аргумент функции Бесселя
к - порядок функции Бесселя
111.
Ω – частота полезного сигналаКомбинационные частоты четные и
нечетные составляющие
112.
Спектр модулированного по углу сигнала113.
Амплитуды гармоник сигналовс угловой модуляцией
114.
115.
Угловые модуляции при цифровом полезном сигналеS( t ) ЧМ A 0cos[ 0 t U( t )dt 0 ];
S( t ) ФМ A 0cos[ 0 t U( t ) 0 ].
U(t)
1
0
1
0
1
В
t
S(t)
ЧМ
t
S(t)
ФМ
t
116.
S(t) 1 AMS(t) 2 AM
a 0
A 0 A n cos(nΩ1 t n ) cosω1 t;
2 n 1
a 0
A 0 A n cos(nΩ 1 t n ) cosω 2 t.
2 n 1
Итоговый спектр ЧМ содержит несущие частоты 1, 2,
в окрестностях каждой из которых расположены боковые полосы,
состоящие из комбинаций частот n
2 n 1
1
1
Δ
Δ
S(t) ФМ A 0 B sin ω1 t
cos
2
2
Δ B
Δ
A 0 sin
(1 cos nπ) sin ω1 nΩ1 t
2 n 1 nπ
2
Δ B
Δ
A 0 sin
(1 cos nπ) sin ω1 nΩ1 t
,
2 n 1 nπ
2
117.
Схемы, иллюстрирующие принципы АМ, ЧМ и ФМ при передачедвоичных символов
118.
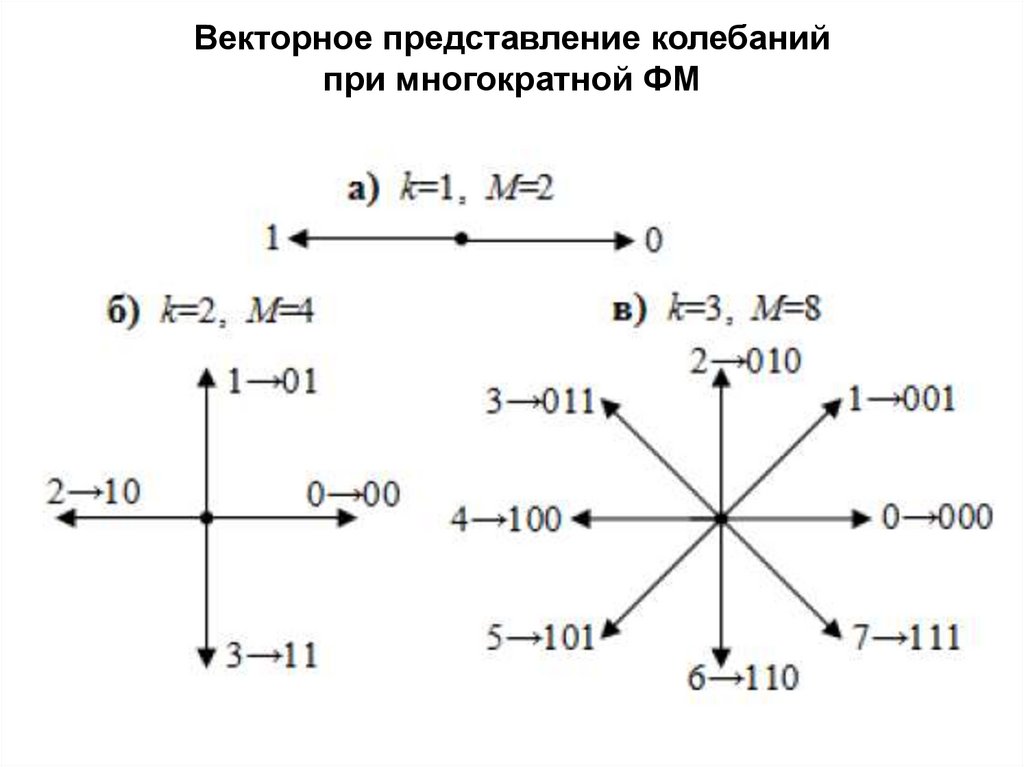
Векторное представление колебанийпри многократной ФМ
119.
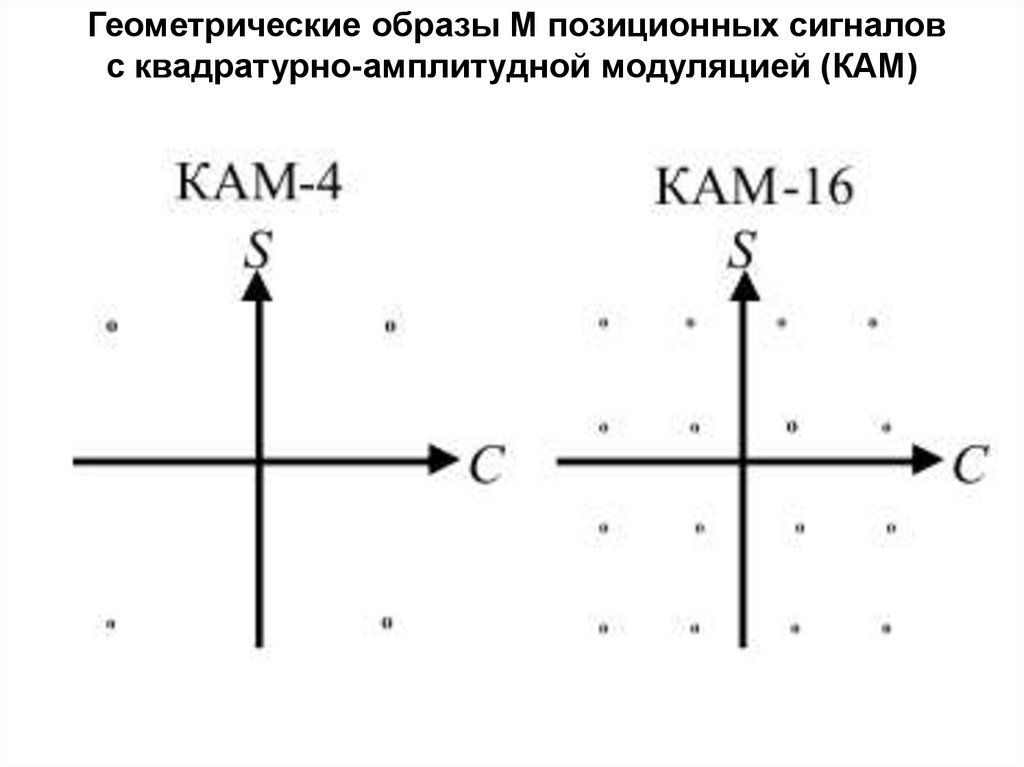
Геометрические образы M позиционных сигналовс квадратурно-амплитудной модуляцией (КАМ)
120.
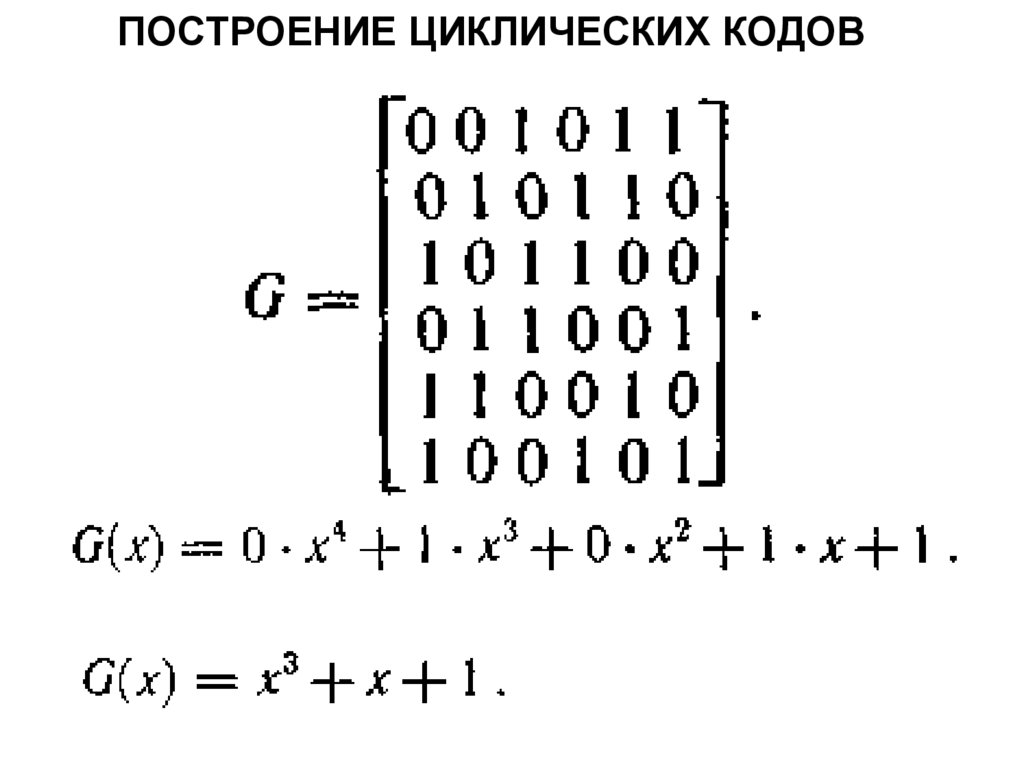
Помехоустойчивые коды121.
ПОСТРОЕНИЕ ЦИКЛИЧЕСКИХ КОДОВ122.
Операция символического умножения1) многочлены перемножаются по обычным правилам, но с приведением
подобных членов по модулю два;
2) если старшая степень произведения не превышает n— 1, то оно и
является результатом символического умножения;
3) если старшая степень произведения больше или равна n, то многочлен
произведения делится на заранее определенный многочлен степени n и
результатом символического умножения считается остаток от деления.
123.
124.
Вычисление проверочного полинома125.
Кодер циклического кодаДекодер циклического кода





































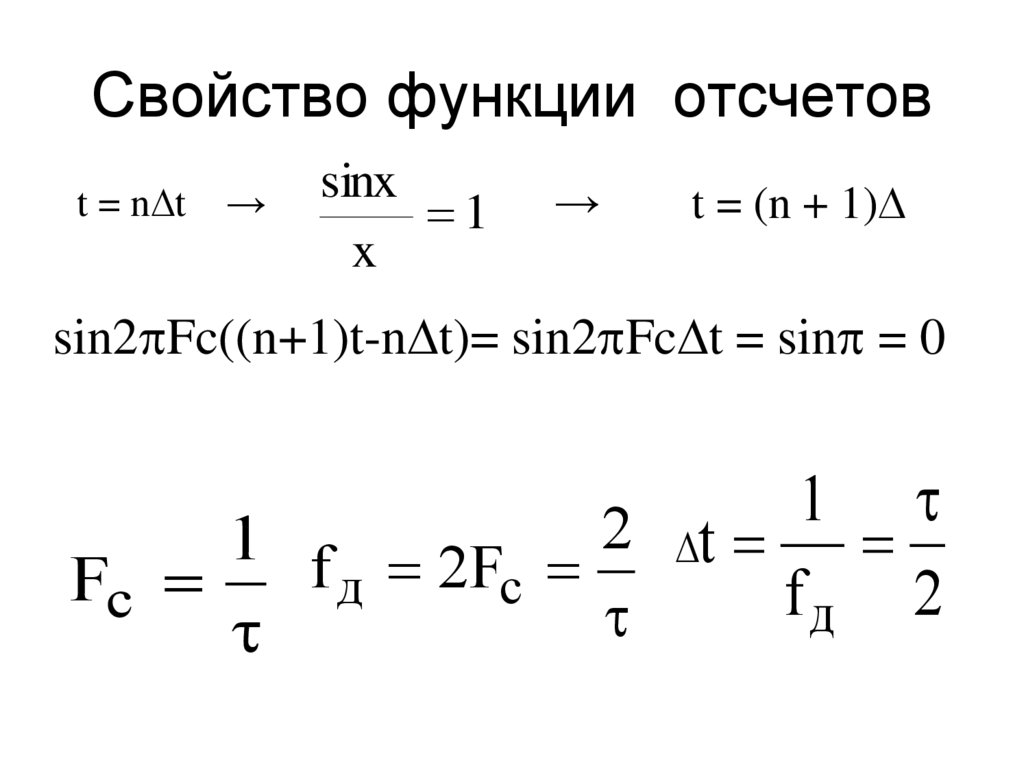
























































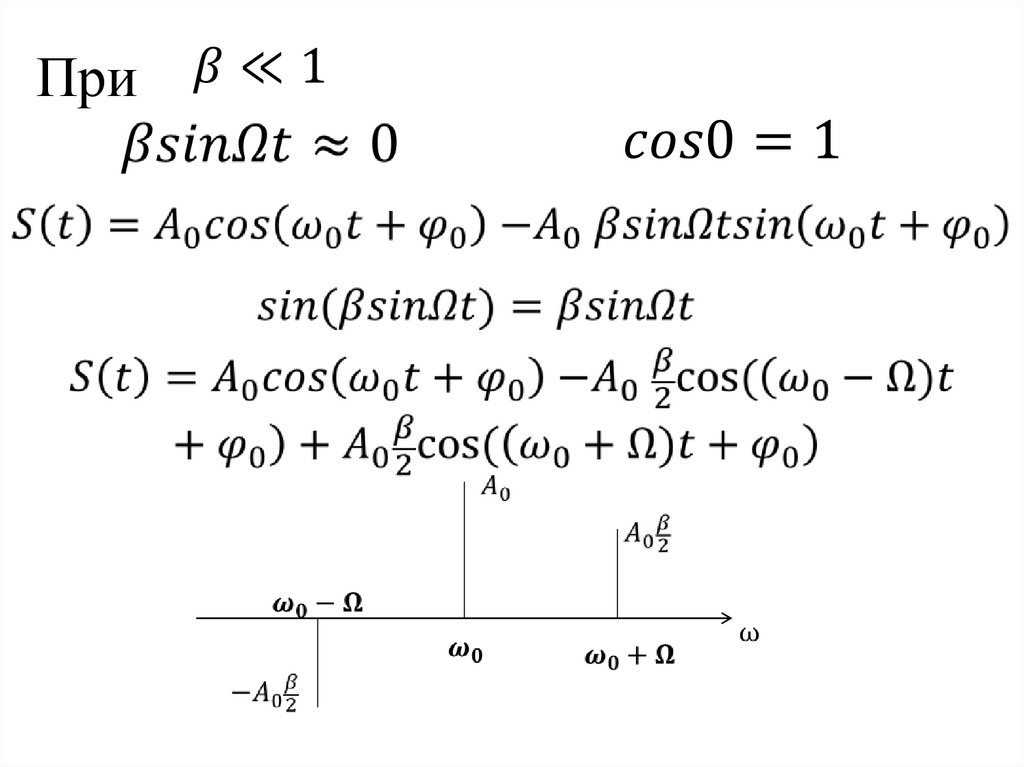













 Электроника
Электроника








