Оценка эффективности и элементы оптимизации систем передачи информации профессор

1.

кафедра информационнотелекоммуникационных систем и технологий
Дисциплина Анализ информационной
безопасности телекоммуникационных систем
Тема 6 Оценка эффективности и элементы оптимизации
систем передачи информации
профессор
Белов Сергей Павлович
1

2.

ЦЕЛЬЮ темы является - изучение вопросов оптимизации
инфокоммуникационных систем. Вводятся и анализируются
критерии оценки и показатели качества работы цифровых
инфокоммуникационных
систем.
Рассматриваются
возможности реальных инфокоммуникационных систем по
достижению предельных значений затрат энергии и полосы
частот на передачу одной двоичной единицы информации.
ЗАДАЧИ лекции:
1 изложение
основных
подходов
к
оптимизации
инфокоммуникационных систем.
Литература
1. Белов, С.П., Жиляков, Е.Г. Анализ информационной безопасности
телекоммуникационных
систем:
Учебно-методический
комплекс. : http://pegas.bsu.edu.ru/course/view.php?id=8360
Белгород, 2015 год.

3.

Анализ эффективности и элементы оптимизации систем цифровой связи
1.1 Основные критерии и показатели качества работы систем связи
Из рассмотрения, проведенного в предыдущих лекциях, следует, что задача цифровой
линии связи состоит в достаточно хорошем «приближении» (в некотором определенном
смысле) принятого множества {
} к переданному множеству {
i }. Иными словами,
i
качество принимаемой информации зависит от степени указанного приближения.
Для количественной оценки этого приближения пользуются вероятностью ошибки
приема отдельного элемента дискретного сообщения или вероятностью ошибки приема
всего дискретного сообщения.
Передача информации с требуемым качеством еще не дает оснований для суждения о
том, хороша или плоха данная линия связи. Всегда желательно, чтобы линия связи
обеспечивала передачу информации с требуемым качеством наиболее «экономно», т. е.
с наименьшими «затратами», понимаемыми в некотором определенном смысле. Под
такими затратами можно понимать затраты мощности, полосы частот, стоимости
оборудования, его веса и т. д. и т. п., которые необходимы для передачи определенного
количества информации (например, одной двоичной единицы).
Для количественной оценки затрат при передаче информации выбирают тот или иной
критерий. Выбор критерия определяется рядом соображений и, как правило,
представляет собой компромисс между стремлением учесть ряд особенностей работы
линий связи и стремлением к простоте и удобству пользования. При выборе критерия
необходимо, учитывать требования и ограничения, которые наложены на некоторые
характеристики и параметры системы связи. В настоящее время в некоторых цифровых
системах ограничивающим фактором первостепенной важности является величина
излучаемой средней или пиковой мощности (например, в системах дальней космической
связи), а в некоторых — используемая полоса частот.
~
x
x

4.

Имеются системы, в которых необходимо учитывать не один, а ряд
ограничивающих факторов (вес, габариты, излучаемая мощность). Выбрать критерий,
который был бы универсальным для любых систем передачи цифровой информации,
трудно. Для одного класса систем лучше подходит один критерий, для другого — другой.
Наиболее широко в настоящее время в теории связи и в прикладных задачах
применяются критерии, в соответствии с которыми системы связи оцениваются
величиной затрат на передачу единицы количества информации при заданном качестве
её приема. Такие критерии можно назвать критериями удельных затрат. В соответствии
с этими критериями лучшей оказывается та система, которая характеризуется меньшими
удельными затратами.
Иногда более удобны критерии, в соответствии с которыми системы связи
оцениваются количеством информации, приходящейся на единицу условных затрат при
заданном качестве приема информации. Такие критерии можно назвать критериями
удельной информации. В соответствии с этими критериями лучшей оказывается та
система, которая характеризуется более высокой удельной информацией.
Нетрудно видеть, что критерии удельных затрат и удельной информации обратны
по отношению друг к другу.
В дальнейшем при оценке качества работы различных систем передачи цифровой
информации и сравнении этих систем между собою будем пользоваться критериями
удельных затрат. Чтобы не усложнять задачу, из всех видов затрат будем учитывать
только затраты энергии и полосы частот на передачу одной двоичной единицы
информации (одного бита).
В соответствии с этим удельные энергетические затраты будем характеризовать
величиной
Е Ео / N о
(1)

5.

где Ео - энергия сигнала на входе приемника, соответствующая передаче одного бита
информации с заданной достоверностью; Nо - спектральная плотность мощности
помехи на входе приемника.
Удельные затраты полосы будем характеризовать величиной
f f ' / R
(2)
где R - информационная скорость передачи (бит/с); f э - эквивалентная полоса
пропускания приемного устройства, соответствующая ширине спектра используемого
сигнала.
Такие критерии впервые были внедрены Сандерсом для оценки качества работы систем
связи, в которых основной помехой являются флуктуационные шумы с равномерной
спектральной плотностью N0. Эти критерии оказались очень удобными и получили
широкое распространение в теории связи и ее приложениях.
Если спектральную плотность нельзя считать равномерной (помеха типа «окрашенного»
шума), можно приближенно пользоваться усредненной величиной удельных затрат
энергии
E E0 / N 0 ( f )
(3)
где Nо(f) —средняя величина спектральной плотности помех в полосе пропускания f э .
Значения E и f , можно рассматривать как обобщенные показатели качества работы
системы связи, оцениваемой в соответствии с критериями затрат.
Как уже указывалось ранее, качество передачи цифровой информации оценивается
достоверностью и скоростью ее передачи. При оценке же качества работы системы
передачи информации наряду с этими абсолютными показателями необходимо также
учитывать обобщенные показатели, рассмотренные выше.

6.

Итак, качество работы системы передачи цифровой информации можно
характеризовать следующими показателями:
1) вероятностью ошибки при приеме одного элемента дискретного сообщения;
2) информационной и технической скоростью передачи сообщений;
3) энергетическими затратами на передачу одной двоичной единицы информации
(удельные затраты энергии);
4) затратами полосы на передачу одной двоичной единицы информации (удельные
затраты полосы).
Необходимо отметить, что перечисленные показатели не затрагивают такие важные
стороны, связанные с технической реализацией систем, как стоимость, вес, габариты и т.
д. Учет этих факторов представляет большую самостоятельную проблему, относящуюся к
области проектирования и конструирования систем. В связи с этим данные вопросы здесь
не рассматриваются.
Помимо задач оптимизации систем, в инженерных приложениях возникает и другая
весьма важная задача — эффективное использование уже действующих линий и каналов
связи, так как в их создание вложены большие средства. Это вызывает значительное
развитие методов защиты передаваемой информации от помех путем помехоустойчивого
кодирования; методов устранения избыточности в передаваемых сообщениях; методов
понижения требуемого отношения сигнал/шум при сохранении заданной точности
передачи информации; совершенствование методов уплотнения и разделения каналов
при многоканальной передаче; совершенствование методов и способов модуляции и
демодуляции и т. д.
Итак, развитие современных систем передачи цифровой информации идет по двум
направлениям:
1) отыскание новых методов и способов передачи и приема информации,
приближающих показатели работы систем к предельно возможным;
2) совершенствование существующих систем с целью их более эффективного
использования.

7.

Однако вполне правомерно при реализации этих направлений задать вопрос: А имеются
ли какие-то
предельные возможности инфокоммуникационных систем или они
бесконечны. Ответ на этот вопрос дает анализ теоремы Шеннона.
Предельные возможности систем связи
Выше указывалось, что с учетом ряда допущений и идеализации К. Шеннону удалось
доказать ряд теорем об оптимальных каналах связи. В частности, для гауссовского
канала с белым шумом и ограниченной средней мощностью сигнала Шеннон получил
широко известную формулу, определяющую максимум средней скорости передачи
информации по такому каналу (пропускную способность канала):
f э log2 (1 Pc / Pш ) f э log2 (1 Pc / N o f э )
(4)
где С - пропускная способность канала;
- ширина полосы частот, занимаемой каналом
(ширина спектра сигнала); Рс - средняя мощность сигнала; Рш -средняя мощность шума в
канале; No- спектральная плотность белого гауссовского шума.
Эта формула характеризует предельные возможности канала, в котором применены
«наилучшие» способы передачи и приема (оптимальное кодирование и декодирование),
обеспечивающие согласование производительности источника информации с
пропускной способностью канала. При этом вся информация, создаваемая источником,
полностью поступает к получателю, т. е. потери информации в канале за счет действия
помех не происходит. Это означает, что между переданным и принятым сообщением
имеется полное соответствие и ошибки отсутствуют. Необходимо отметить, что формула
(4) справедлива только при физически нереализуемых условиях: бесконечном времени
передачи информации (бесконечное время кодирования приводит к бесконечному
времени задержки поступления информации к потребителю) и неизменных условиях
работы канала, т.е. формулу (4) нужно рассматривать как асимптотическое соотношение,
определяющее физически недостижимую границу скорости передачи информации.

8.

В каналах, где кодирование неоптимальное (или отсутствует вовсе), скорость передачи
меньше пропускной способности канала, а ошибка при передаче информации не равна
нулю.
Несмотря на существенные отличия условий работы реальных каналов связи от условий
работы оптимальных, в смысле К. Шеннона, каналов, очень интересно, как было сказано
выше, выяснить предельные возможности оптимальных каналов и установить границы,
которые принципиально не могут быть превзойдены ни при каких способах передачи и
приема.
В соответствии с введенными критериями будем характеризовать затраты энергии и
полосы на передачу одной двоичной единицы информации в оптимальном (идеальном)
канале величинами
Е Ео / N о = Pc T0 / N 0
(5)
f f ' / R max = f э /C
(6)
где Eо и Tо - энергия сигнала и время, соответствующие передаче одной двоичной
единицы информации в идеальном канале.
Приняв во внимание, что по определению
(7)
и учитывая выражения (5) и (6), формулу (4) нетрудно преобразовать к виду
( f э / С) log2 (1 ( Eo / N o ) (C / fэ)) 1
(8)
После несложных преобразований последнее выражение можно привести к виду
1 / f
E f (2
1)
(9)
Выражение (9) определяет функциональную связь между удельными затратами энергии
и полосы в идеальном гауссовском канале связи.

9.

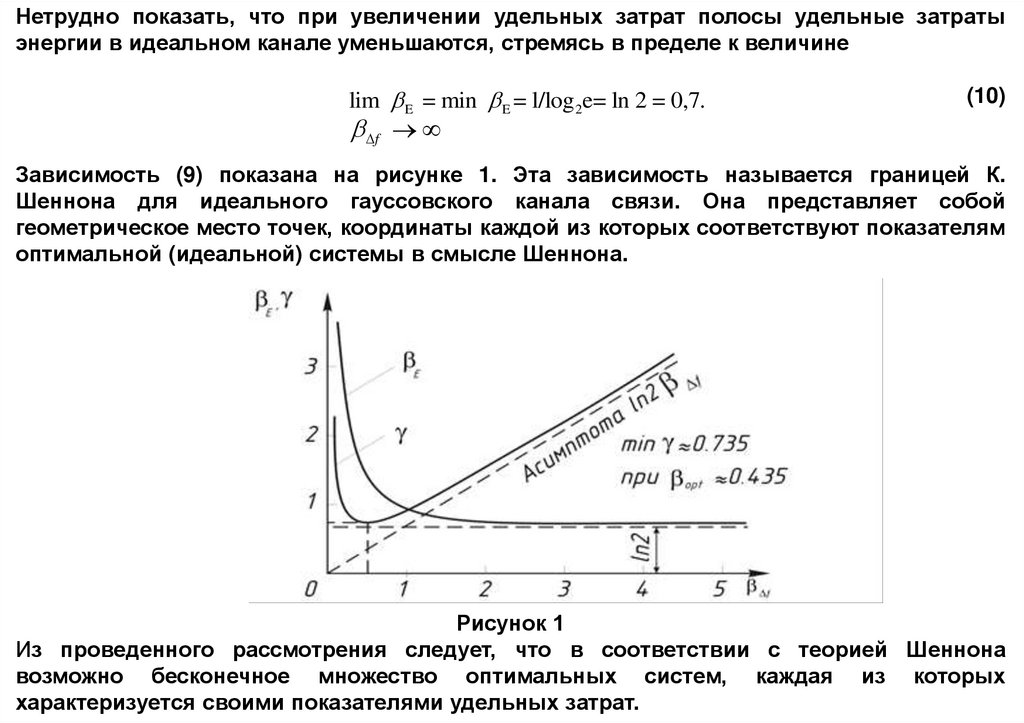
Нетрудно показать, что при увеличении удельных затрат полосы удельные затраты
энергии в идеальном канале уменьшаются, стремясь в пределе к величине
lim E = min E = l/log 2e= ln 2 = 0,7.
(10)
f
Зависимость (9) показана на рисунке 1. Эта зависимость называется границей К.
Шеннона для идеального гауссовского канала связи. Она представляет собой
геометрическое место точек, координаты каждой из которых соответствуют показателям
оптимальной (идеальной) системы в смысле Шеннона.
Рисунок 1
Из проведенного рассмотрения следует, что в соответствии с теорией Шеннона
возможно бесконечное множество оптимальных систем, каждая из которых
характеризуется своими показателями удельных затрат.

10.

График на рисунке 1 показывает, что желание улучшить один из показателей
приводит к неизбежному ухудшению другого. Оптимальные системы с малыми
затратами энергии требуют значительных затрат полосы и, наоборот, системы с
малыми затратами полосы — значительных затрат энергии. Так как показатели
реальных систем не могут быть выше показателей оптимальных систем, то
принципиально реализуемым системам связи соответствуют только те точки
плоскости, которые лежат в области выше границы Шеннона.
Используя выводы, полученные из теории К. Шеннона, которые имеют
принципиальное значение, так как указывают пути решения ряда важных задач
прикладного характера и, в частности, к задаче выбора вида сигнала. Важность
решения этой задачи объясняется тем, что показатели качества работы
проектируемой информационной системы существенно зависят от того, насколько
правильно выбран вид сигнала с учетом специфики области применения,
конкретных требований к данной системе, а также ограничений, наложенных на
некоторые ее характеристики и параметры. Указанные обстоятельства делают
задачу выбора вида сигнала весьма сложной. Естественно, что при решении этой
задачи приходится прибегать к некоторым упрощениям и допущениям, и поэтому
нет полной уверенности, что найденные сигналы близки к оптимальным для
данной информационной системы. Отмеченные трудности можно уменьшить,
если рассмотреть проблему выбора сигналов в идеальных каналах связи и
установить особенности различных возможных классов сигналов в таких каналах.
Очевидно, что в реальных каналах класс возможных сигналов не может быть
шире, чем в идеальных. Следовательно, открываются пути отыскания таких
видов сигналов, которые в данных конкретных условиях и при некоторых

11.

Рассмотрим затронутую выше проблему подробнее. Из общей теории информации
известно, что максимальная средняя производительность Ht стационарного источника
дискретной информации определяется величиной
(11)
где М - число различных сообщений длительностью Т, вырабатываемых дискретным
источником.
В наиболее интересном с точки зрения практики частном случае, когда источник,
располагающий алфавитом из n символов, вырабатывает сообщения, каждое из которых
состоит из m символов одинаковой длительности τ0 , выражение (11) принимает вид
m
(12)
Это выражение показывает, что максимальная производительность источника дискретной
информации в данном частном случае определяется только основанием алфавита п и
длительностью информационного символа
.
В оптимальном (идеальном) по К. Шеннону канале связи источник информации всегда
согласован с каналом, т. е. его производительность равна пропускной способности
канала:
(13)
Учитывая это условие и выражение (7), получим
(14)
Отсюда следует
(15)
Последнее выражение устанавливает связь между временем То, затрачиваемым на
передачу одной двоичной единицы информации, и длительностью
информационного
символа.

12.

Полученное выражение позволяет записать удельные затраты полосы в идеальном
канале в виде
(16)
=Б /log n.
f
с
2
Выбор сигналов с малыми затратами полосы частот
В этом случае используемые сигналы характеризуются соотношением
(17)
откуда следует условие
n 2
Бс
(18)
Условие (18) означает, что если применять сложные сигналы с большой базой (Бс>>1), то
необходимо использовать огромные основания алфавита. Очевидно, что в данном
случае это практически неприемлемый путь решения задачи.
Если применять сигналы с минимально возможной базой (Бс=1), то в рассматриваемом
случае
1 / f
(19)
n 2
2
Из этого выражения следует, что для получения малых затрат полосы необходимо
выбирать сигналы с минимально возможной базой и использовать алфавиты с
основанием больше двух. Сигналы, удовлетворяющие таким условиям, называются
многоосновными (много алфавитными). К таким сигналам, в частности, относятся
сигналы с многократной фазовой манипуляцией.
Естественно, что, стремясь выбрать сигналы с малыми затратами полосы, нельзя
забывать о том, что при этом могут потребоваться значительные затраты энергии.
Представление о величине затрат в идеальной системе для простых сигналов с
различными основаниями можно получить из таблице 1, рассчитанной по формулам (9) и
(16).

13.

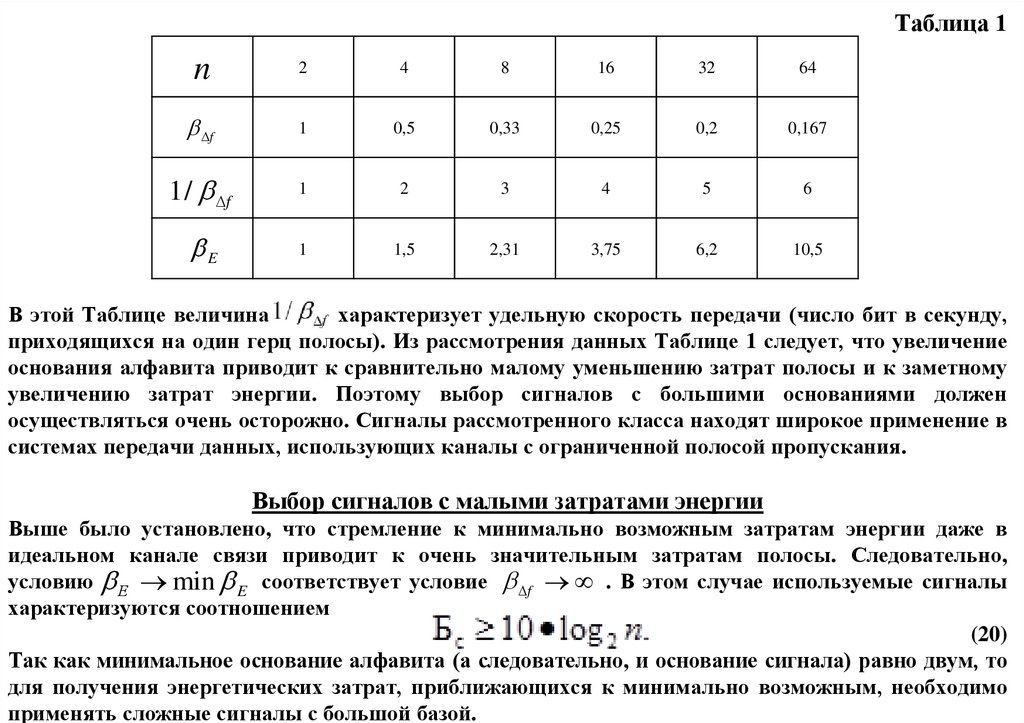
Таблица 1
n
2
4
8
16
32
64
f
1
0,5
0,33
0,25
0,2
0,167
1 / f
1
2
3
4
5
6
E
1
1,5
2,31
3,75
6,2
10,5
В этой Таблице величина
характеризует удельную скорость передачи (число бит в секунду,
приходящихся на один герц полосы). Из рассмотрения данных Таблице 1 следует, что увеличение
основания алфавита приводит к сравнительно малому уменьшению затрат полосы и к заметному
увеличению затрат энергии. Поэтому выбор сигналов с большими основаниями должен
осуществляться очень осторожно. Сигналы рассмотренного класса находят широкое применение в
системах передачи данных, использующих каналы с ограниченной полосой пропускания.
Выбор сигналов с малыми затратами энергии
Выше было установлено, что стремление к минимально возможным затратам энергии даже в
идеальном канале связи приводит к очень значительным затратам полосы. Следовательно,
условию Е min E соответствует условие f . В этом случае используемые сигналы
характеризуются соотношением
(20)
Так как минимальное основание алфавита (а следовательно, и основание сигнала) равно двум, то
для получения энергетических затрат, приближающихся к минимально возможным, необходимо
применять сложные сигналы с большой базой.

14.

Однако расчеты показывают, что условие (20) слишком жесткое, так как энергетические
затраты очень близки к минимально возможным уже при n=2 и Бс=10, т.е. величина
E практически совпадает с минимально возможным значением затрат энергии.
Возникает вопрос, какой же смысл в том, чтобы применять сигналы с большой базой,
если увеличение базы сигнала практически не снижает энергетические затраты и только
увеличивает затраты полосы? Дело в том, что сложные сигналы обладают рядом
важных свойств, которые особенно ярко проявляются при больших значениях базы.
Одно из таких свойств состоит в том, что прием подобных сигналов принципиально
возможен при очень малом отношении сигнала к шуму на входе приемника.
Это означает, что принимаемый сигнал будет «замаскирован» шумами. Отмеченное
свойство сложных сигналов с большой базой открывает принципиальные возможности
построения таких систем связи, работу которых трудно обнаружить. Несмотря на
большие трудности технической реализации информационные системы со сложными
сигналами находят применение в области управления, в космической радиосвязи и т. п.
Выше были рассмотрены некоторые вопросы выбора вида сигнала в идеальных
каналах связи для двух крайних случаев:
1)
когда желательно иметь малые затраты полосы;
2)
когда желательно иметь малые затраты энергии при передаче информации.
Однако имеется ряд систем (в частности, некоторые космические системы, радио - и
гидротелеметрические системы) при реализации которых существенное значение имеют
оба указанных фактора. В таких случаях желательно выбрать класс сигналов, который
обеспечивал бы сравнительно малые затраты и полосы и энергии.
Рассмотрим эту задачу применительно к идеальному каналу связи. Чтобы учесть оба
вида затрат, введем обобщенный показатель качества (обобщенные удельные затраты)
E , f f * E

15.

С учетом выражения (9) для идеальной системы этот показатель принимает вид
1 / f
E , f 2 f * (2
1)
(21)
График зависимости обобщенных затрат от величины f приведен на рисунок 1. Он
представляет собой геометрическое место точек, координаты каждой из которых
соответствуют показателям оптимальной системы.
Кривая разбивает всю плоскость (
) на две части. Все точки, лежащие выше
кривой, относятся к принципиально реализуемым системам. Из рассмотрения графика
следует, что при некоторой величине
обобщенные затраты в оптимальной системе
достигают минимума. Расчеты показывают, что min E , f 0,735 при f 0,435 .
В области
= 0,35 - 0,5 величина обобщенных затрат мало отличается от минимального
значения. Указанная область соответствует классу простых сигналов с основаниями от
четырех до восьми (п=4—8). Если ограничить обобщенные затраты величиной E , f 1 ,
то область возможных простых сигналов расширится от п = 2 до п =16, т. е. охватит весь
класс простых многоосновных сигналов, представляющих практический интерес.
Проведенное рассмотрение возможных дискретных сигналов в идеальных по К. Шеннону
каналах связи может служить хорошим ориентиром при решении ряда практических
задач по выбору наиболее подходящего для заданных требований класса сигналов.
Дальнейшая оптимизация информационной системы может быть сведена к выбору
конкретного вида сигналов в пределах наиболее подходящего класса таких сигналов.
В заключение отметим, что показатели качества работы лучших современных цифровых
систем связи еще заметно уступают показателям оптимальных систем, особенно по
удельным затратам энергии. Это обусловлено рядом причин, некоторые из которых
ранее уже упоминались. К числу таких причин в первую очередь относятся не
идеальность характеристик реальных систем, приводящая к дополнительным
искажениям сообщений, и не оптимальность используемых методов и способов
передачи и приема информации.

16.

Вопросы для повторения
1.
2.
3.
4.
5.
6.
Назовите характерные особенности простых и сложных сигналов.
В каких системах целесообразно применять простые сигналы, а в каких
сложные
Поясните, что понимается под основными сигналами
Какими свойствами обладают многоосновные сигналы
При каких значениях E , f , f системы передачи информации принципиально
реализуемы
Какие причины не позволяют в реальных каналах телекоммуникаций достичь
предельных значений эффективности по энергетическим и частотным
параметрам