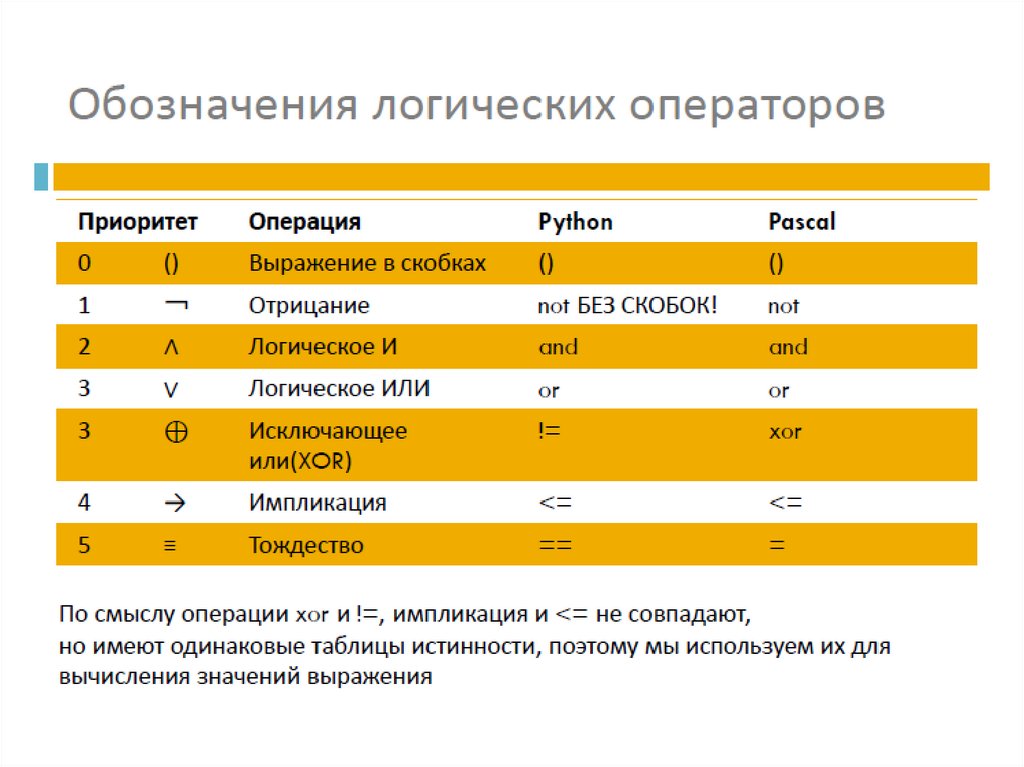
Обозначения логических операторов. Задача №15

1.

2.

3.

Обозначим через m & n поразрядную конъюнкцию
неотрицательных целых чисел m и n.
Так, например, 14 & 5 = 11102 & 01012 = 01002 = 4. Для какого
наименьшего неотрицательного целого числа А формула
x & 29 ≠ 0 → (x & 17 = 0 → x & А ≠ 0)
тождественно истинна (т. е. принимает значение 1 при любом
неотрицательном целом значении переменной x)?

4.

Обозначим через m&n поразрядную конъюнкцию
неотрицательных целых чисел m и n.
Так, например, 14&5 = 11102&01012 = 01002 = 4.
Для какого наименьшего неотрицательного целого
числа А формула
тождественно истинна (то есть принимает значение 1 при
любом неотрицательном целом значении переменной x)?

5.

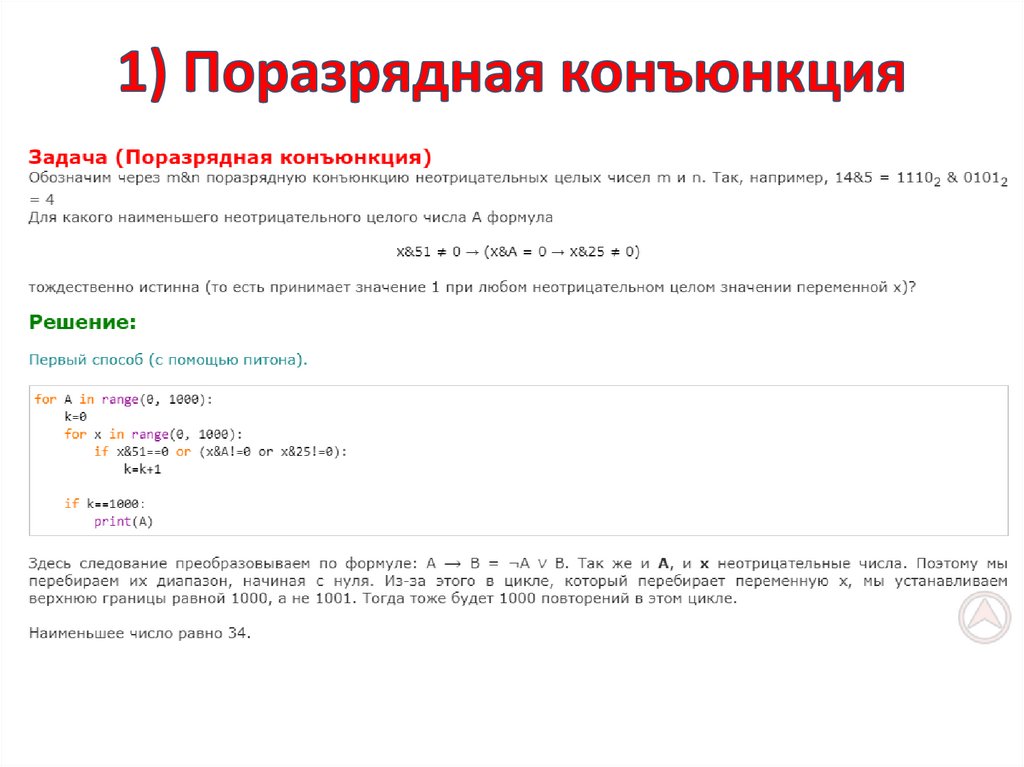
Обозначим через m&n поразрядную конъюнкцию
неотрицательных целых чисел m и n.
Так, например, 14&5 = 11102&01012 = 01002 = 4.
Для какого наибольшего целого числа А формула
x&51 = 0 ∨ (x&41 = 0 → x&А = 0)
тождественно истинна (т. е. принимает значение 1 при
любом неотрицательном целом значении переменной x)?

6.

7.

Отрезки на Питоне
3

8.

44

9.

20

10.

22

11.

25

12.

6

13.

На числовой прямой даны два отрезка: P = [5, 30]
и Q = [14, 23]. Укажите наибольшую возможную
длину промежутка A, для которого формула
((x ∈ P) ≡ (x ∈ Q)) → ¬(x ∈ A)
тождественно истинна, то есть принимает
значение 1 при любом значении переменной х.

14.

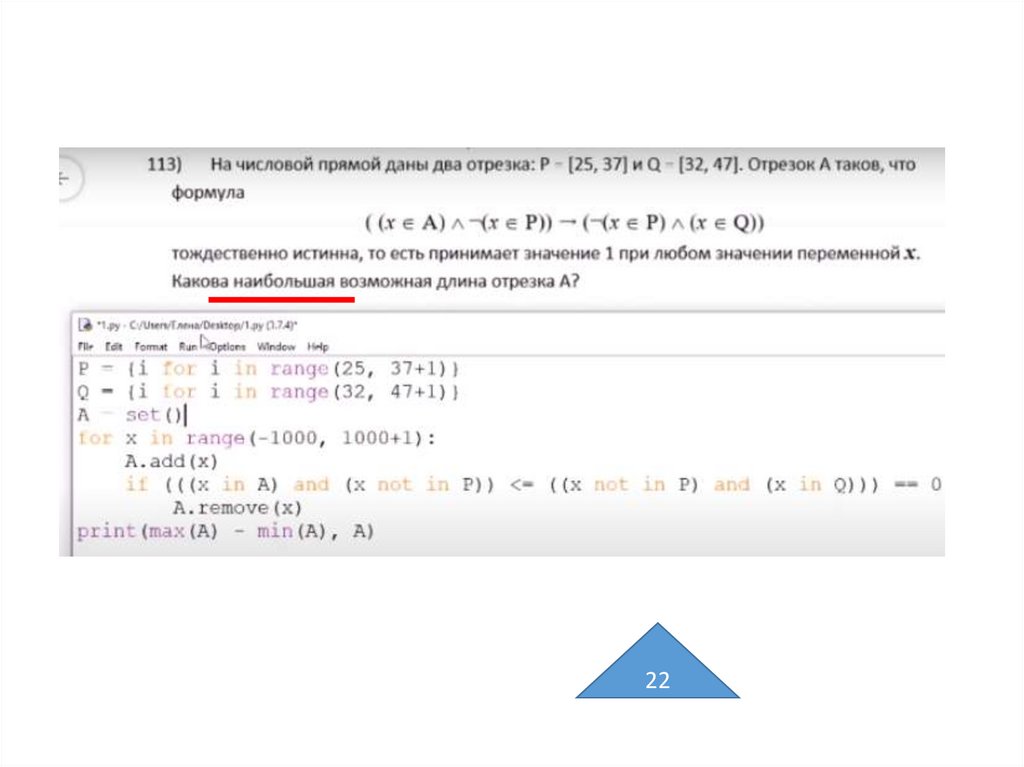
На числовой прямой даны два отрезка: P = [25; 50] и
Q = [32; 47]. Укажите наибольшую возможную длину
промежутка A, для которого формула
(¬ (x є A) → (x є P)) → ((x єA) → (xєQ))
тождественно истинна, то есть принимает значение 1
при любом значении переменной х.

15.

На числовой прямой даны два отрезка: Р = [30,
45] и Q = [40, 55]. Какова наименьшая возможная
длина интервала A, что обе приведённые ниже
формулы истинны при любом значении
переменной х:
( ¬(x ∈ A) → (¬(x ∈ P)) )
((x ∈ Q)→ (x ∈ A))

16.

Ответ 15

17.

Для какого наибольшего целого числа А формула
((x ≤ 9) →(x ⋅ x ≤ A)) ⋀ ((y ⋅ y ≤ A) → (y ≤ 9))
тождественно истинна, то есть принимает значение 1
при любых целых неотрицательных x и y?

18.

Сколько существует целых значений
числа A, при которых формула
((x < A) → (x2 < 81)) ∧ ((y2 ≤ 36) → (y ≤ A))
тождественно истинна при любых целых
неотрицательных x и y?
Ответ: 4

19.

20.

21.

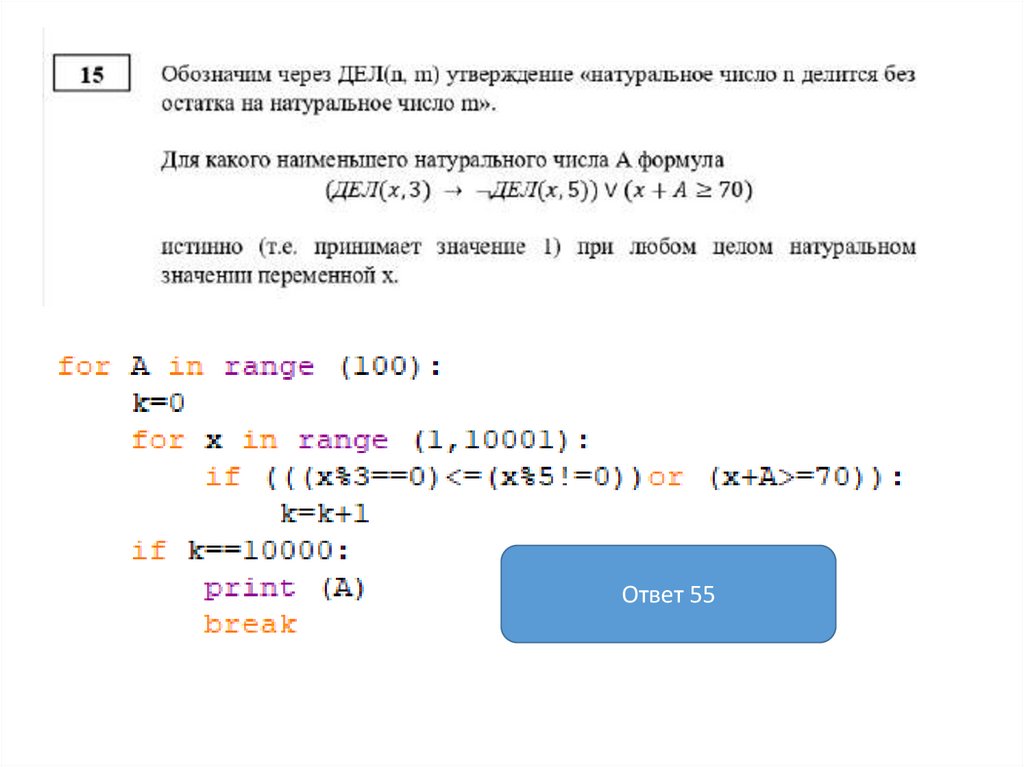
Обозначим через ДЕЛ(n, m) утверждение «натуральное
число n делится без остатка на натуральное число m».
Для какого наибольшего натурального числа А формула
(A < 50) ∧ (¬ДЕЛ(x, А) → (ДЕЛ(x, 10) → ¬ДЕЛ(x, 18)))
тождественно истинна (то есть принимает значение 1 при
любом натуральном значении переменной x)?
Самостоятельно
Ответ: 45

22.

23.

Функция all() возвращает значение True , если все элементы в итерируемом
объекте - истинны, в противном случае она возвращает значение False.
Если передаваемая последовательность пуста, то функция all() также
возвращает True.

24.

25.

26.

27.

28.

Ответ 55