Похожие презентации:
Теоретический материал. Логика и алгоритмы
1.
Теоретический материалЛогика и алгоритмы
Доцент кафедры АЭМИС
к.т.н. Кечкина Наталия Игоревна
2.
Упрощение логических выраженийЗамена операции на их выражения через И, ИЛИ
и НЕ:
A B A B
A B A B A B
Инверсия сложных
Моргана:
выражений
A B A B,
по
формулам
де
A B A B
3
3.
Задания Побитовая конъюнкция№ 9804
Обозначим через m & n поразрядную конъюнкцию неотрицательных целых
чисел m и n. Так, например, 14 & 5 = 11102 & 01012 = 01002 = 4. Для какого
наименьшего неотрицательного целого числа А формула
x & 29 ≠ 0 → (x & 17 = 0 → x & А ≠ 0)
тождественно истинна (т. е. принимает значение 1 при любом
неотрицательном целом значении переменной x)?
Z29= x & 29 =0
Z17= x & 17 = 0
ZA= x & А = 0
¬ Z29 → (Z17 → ¬ ZA )= Z29 +(¬Z17+ ¬ ZA )= Z29 +¬(Z17*ZA)= ¬(Z17*ZA)+ Z29 =
= (Z17*ZA) → Z29
Z17ZA →Z29
Z(17 or A) →Z29
29=111012
1
0
0
0
1 Z17
17=100012
+
0
1
1
0
0 A
Amin=11002=12
ОТВЕТ: 12
1
1
1
0
1
Z29
4
4.
Задания Побитовая конъюнкция№ 9804
Обозначим через m & n поразрядную конъюнкцию неотрицательных целых
чисел m и n. Так, например, 14 & 5 = 11102 & 01012 = 01002 = 4. Для какого
наименьшего неотрицательного целого числа А формула
x & 29 ≠ 0 → (x & 17 = 0 → x & А ≠ 0)
тождественно истинна (т. е. принимает значение 1 при любом
неотрицательном целом значении переменной x)?
ОТВЕТ: 12
5
5.
Задания Числовые отрезки№ 7763
На числовой прямой даны два отрезка: P = [5, 30] и Q = [14, 23]. Укажите
наибольшую возможную длину промежутка A, для которого формула
((x ∈ P) ≡ (x ∈ Q)) → ¬(x ∈ A)
тождественно истинна, то есть принимает значение 1 при любом значении
переменной х.
A ( x) B( x) 1
A ( x) B( x) 1
P≡x∈P
Amax B
Q≡x∈Q
min
A≡x∈A
(P ≡ Q) → ¬A= (¬P* ¬Q+ P* Q) → ¬A = (¬(P+Q)+ P* Q) → ¬A =
= ¬(¬(P+Q)+ P* Q) + ¬A = ¬ ¬(P+Q)* ¬(P* Q) + ¬A =
= (P+Q)* (¬ P+ ¬ Q) + ¬A
(P+Q)* (¬ P+ ¬ Q) + ¬A =1
Amax= (P+Q)* (¬ P+ ¬ Q)
(P+Q) [5,30]
(¬ P+ ¬ Q)
x<14, x>23
(P+Q)* (¬ P+ ¬ Q)
[5,14) , (23, 30]
Наибольшая возможная длина A 14-5=9
ОТВЕТ: 9
A
B
6
6.
Задания Числовые отрезки№ 13745
Для какого наибольшего целого числа А формула
((x ≤ 9) →(x ⋅ x ≤ A)) ⋀ ((y ⋅ y ≤ A) → (y ≤ 9))
тождественно истинна, то есть принимает значение 1 при любых целых
неотрицательных x и y?
((x ≤ 9) →(x ⋅ x ≤ A)) ⋀ ((y ⋅ y ≤ A) → (y ≤ 9))=
=(¬(x ≤ 9) +(x ⋅ x ≤ A)) ⋀ (¬(y ⋅ y ≤ A) + (y ≤ 9))=
=( (x > 9) +(x ⋅ x ≤ A)) ⋀ ( (y ⋅ y > A) + (y ≤ 9))
( (x > 9) +(x ⋅ x ≤ A)) ⋀ ( (y ⋅ y > A) + (y ≤ 9))=1
( (x > 9) +(x ⋅ x ≤ A)) =1
( (y ⋅ y > A) + (y ≤ 9))=1
ОТВЕТ: 99
7
7.
Задания Числовые отрезки№ 13745
Для какого наибольшего целого числа А формула
((x ≤ 9) →(x ⋅ x ≤ A)) ⋀ ((y ⋅ y ≤ A) → (y ≤ 9))
тождественно истинна, то есть принимает значение 1 при любых целых
неотрицательных x и y?
ОТВЕТ: 99
8
8.
Задания№ 7929
Элементами множеств А, P, Q являются натуральные числа, причём P = {2, 4,
6, 8, 10, 12, 14, 16, 18, 20}, Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}. Известно, что
выражение
( (x ∈ A) → (x ∈ P) ) ∧ ( (x ∈ Q) → ¬(x ∈ A) )
истинно (то есть принимает значение 1) при любом значении переменной х.
Определите наибольшее возможное количество элементов в множестве A.
( (x ∈ A) → (x ∈ P) ) ∧ ( (x ∈ Q) → ¬(x ∈ A) )
A= x ∈ A
P= x ∈ P
Q= x ∈ Q
( A → P ) ∧ ( Q → ¬ A )= (¬ A + P ) ∧ (¬ Q + ¬ A )=
=(¬ A + P ) ∧ (¬ A + ¬Q)= ¬ A+ P∧¬Q
¬ A+ P∧¬Q=1
¬ A=¬( P∧¬Q)
A=P∧¬Q
P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}
A={2,4,8,10,14,16,20}
ОТВЕТ: 7
9
9.
Задания№ 23916
Для какого наименьшего целого неотрицательного числа А выражение
(x + 2y < A) ∨ (y > x) ∨ (x > 20)
тождественно истинно, т. е. принимает значение 1 при любых целых
неотрицательных x и y?
(x + 2y < A) ∨ (y > x) ∨ (x > 20)=1
x + 2y < A
y>x
x > 20
x + 2y =A
y=x
x=20
y=(x-A)/2
x=20, y=20, тогда x+2y=60 и x+2y<A,
т.е. A>60
Amin=61
ОТВЕТ: 61
10
10.
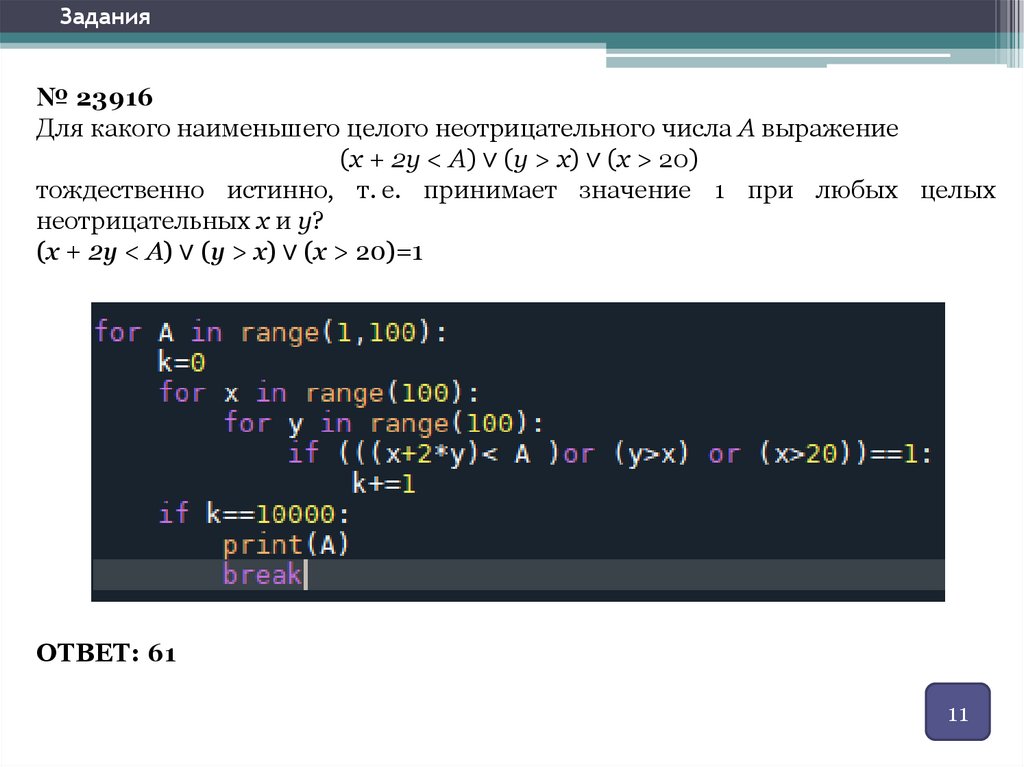
Задания№ 23916
Для какого наименьшего целого неотрицательного числа А выражение
(x + 2y < A) ∨ (y > x) ∨ (x > 20)
тождественно истинно, т. е. принимает значение 1 при любых целых
неотрицательных x и y?
(x + 2y < A) ∨ (y > x) ∨ (x > 20)=1
ОТВЕТ: 61
11
11.
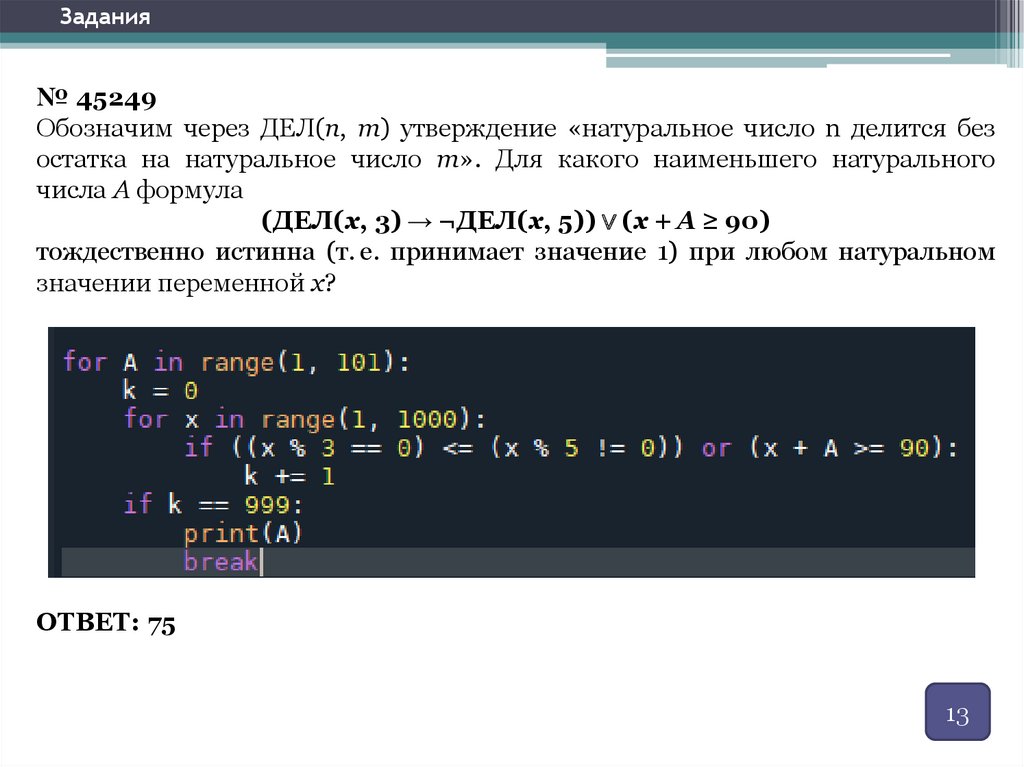
Задания№ 45249
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без
остатка на натуральное число m». Для какого наименьшего натурального
числа А формула
(ДЕЛ(x, 3) → ¬ДЕЛ(x, 5)) ∨ (x + A ≥ 90)
тождественно истинна (т. е. принимает значение 1) при любом натуральном
значении переменной x?
(ДЕЛ(x, 3) → ¬ДЕЛ(x, 5)) ∨ (x + A ≥ 90)=1
(ДЕЛ(x, 3) → ¬ДЕЛ(x, 5))=0
P = ДЕЛ(x, 3)
Q = ДЕЛ(x, 5)
P→ ¬Q=0
¬P+¬Q=0
¬(P*Q)=0
P*Q=1
НОК=15
x + A ≥ 90
A ≥90-x
A ≥90-15=75
Amin=75
12
ОТВЕТ: 75
12.
Задания№ 45249
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без
остатка на натуральное число m». Для какого наименьшего натурального
числа А формула
(ДЕЛ(x, 3) → ¬ДЕЛ(x, 5)) ∨ (x + A ≥ 90)
тождественно истинна (т. е. принимает значение 1) при любом натуральном
значении переменной x?
ОТВЕТ: 75
13










 Математика
Математика








