Похожие презентации:
Модуль 3. Формальные теории и исчисления. Задачи 3.2. Решение задач на вывод формул в исчислении предикатов
1.
Модуль 3Формальные теории и
исчисления
Задачи 3.2. Решение задач
на вывод формул в
исчислении предикатов
2020 г.
2.
Содержание1.
Определение области истинности
предикатов
2.
Доказательство равносильности
3.
Доказательство общезначимости
3.
Задача №1Определить область истинности
предикатов
Q(x)&P(x)
Q( x ) P ( x )
Q( x ) P ( x )
если предикаты P(x) и Q(x) заданы
на множестве натуральных чисел N:
P(x): «число Х делится на 5»
Q(x): «число Х четное»
4.
Решение задачи №1Так как Ip = {5, 10, 15, 20, …. 5n, …}
и IQ = {2, 4, 6, 8, 10, … 2n, …}, то:
{10, 20,… 10n,…}
I Q P I Q I P {2,4,5,6,8,10,...2n,5n,..}
I
Q P
I I ={5, 10, 15,… ,5n, ..} U {1, 3, 5, … 2n-1,
Q
P
..}= {1, 3, 5, 7, 9, 10, … 2n-1,5n, ..}
5.
Задача №2Определить область истинности
предиката ,
x ( P( x ) & Q( x ) R( x ))
если предикаты P(x), Q(x) и R(x)
заданы на множестве натуральных
чисел N:
P(x): «число Х делится на 5»
Q(x): «число Х делится на 3»
R(x): «число Х четное»
6.
Решение задачи №21. Представим предикат через <-, v, &>
x ( P( x ) & Q( x ) R( x ))
x ( P( x ) & Q( x ) R( x ))
x ( P( x ) Q( x ) R( x ))
2. Область истинности предиката представляется
объединением
I p IQ I r
7.
Решение задачи №23. Рассмотрим полученные области истинности
P(x) : «число Х не делится на 5»
Q(x) : «число Х
не делится на 3»
R(x): «число Х четное»
I p IQ I r ={1,2,3,4,6,7,…} U {1,2,4,5,7,…}U
U {2,4,6,8,10,…} = 1,2,3,…,14,16,…,29,30,31,…}=
N / I3*5*( 2 k 1 )
N- множество натуральных чисел
3*5*(2k+1) – множество нечетных чисел, кратных 3 и 5
8.
Задача №3Найти область истинности
предиката
x2 2x 1
P: 2
0
x 3x 2
9.
Решение задачи №31. Найдем область, на которой данный
предикат может быть определен
Поскольку знаменатель дроби не
может быть равен 0, то
x 1, x 2
10.
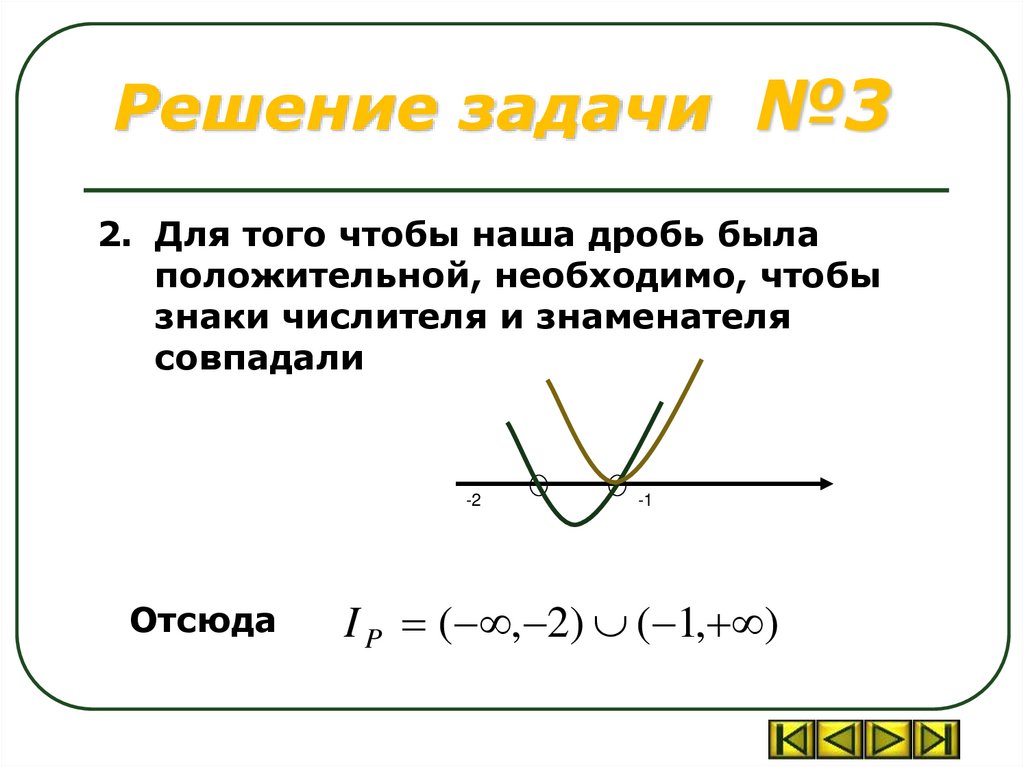
Решение задачи №32. Для того чтобы наша дробь была
положительной, необходимо, чтобы
знаки числителя и знаменателя
совпадали
-2
Отсюда
-1
I P ( , 2) ( 1, )
11.
Задача №4Показать равносильность
формулы
x( P ( x ) & Q( x )) xP ( x ) & xQ( x )
12.
Решение задачи №41. Если предикаты P(x) и Q(x) тождественно
истинны,
то тождественно истинен
предикат
P ( x ) & Q( x ) , а поэтому, будут
истинны высказывания
xP ( x )
xQ( x )
x( P ( x ) & Q( x ))
2. Если один из предикатов, например, P(x),
будет не тождественно истинен, то предикат
P( x ) & Q( x ) не будет тождественно истинен,
следовательно, ложными будут высказывания
xP ( x )
x( P ( x ) & Q( x ))
13.
Решение задачи №43. Если оба предиката P(x) и Q(x) не будут
тождественно истинны, то не будет
тождественно истинен предикат P ( x ) & Q( x )
Следовательно, будут ложными высказывания
xP ( x )
xQ( x )
x( P ( x ) & Q( x ))
4. Следовательно, обе части равносильности
равны при любых значениях P(x) и Q(x)
x( P ( x ) & Q( x )) xP ( x ) & xQ( x )
14.
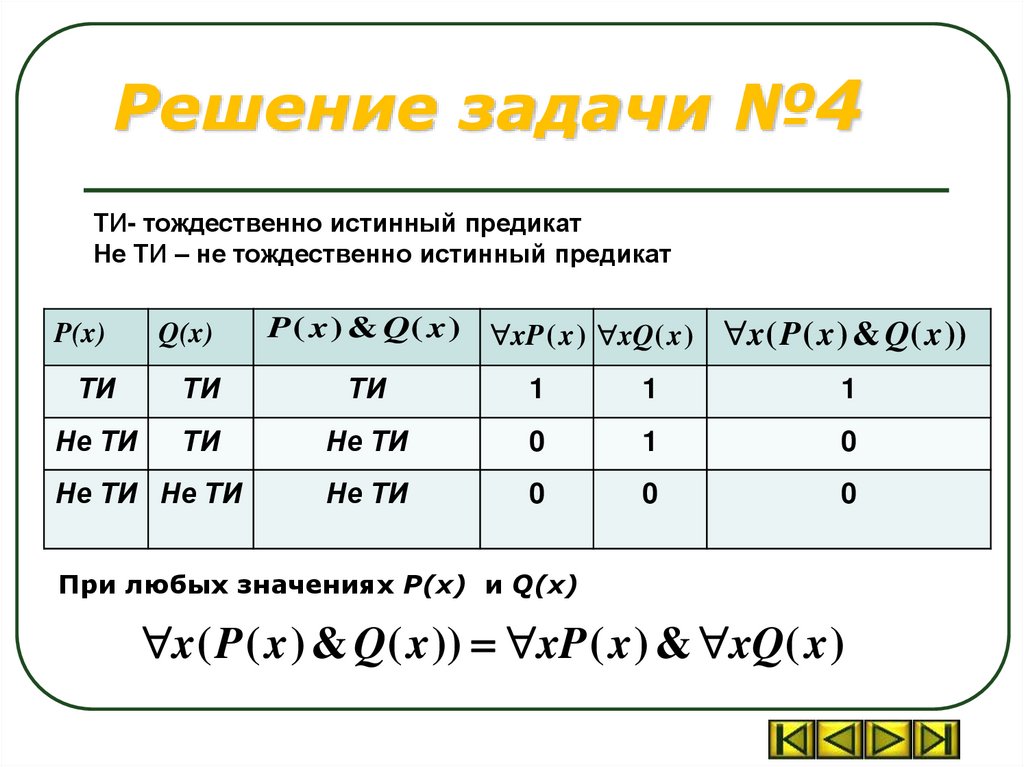
Решение задачи №4ТИ- тождественно истинный предикат
Не ТИ – не тождественно истинный предикат
P ( x ) & Q( x ) xP ( x ) xQ( x ) x ( P ( x ) & Q( x ))
P(x)
Q(x)
ТИ
ТИ
ТИ
1
1
1
Не ТИ
ТИ
Не ТИ
0
1
0
Не ТИ
0
0
0
Не ТИ Не ТИ
При любых значениях P(x) и Q(x)
x( P ( x ) & Q( x )) xP ( x ) & xQ( x )
15.
Задача №5Показать равносильность
формулы
x( P( x) Q( x)) xP( x) xQ( x)
16.
Решение задачи №51. Если предикаты P(x) и Q(x) тождественно
ложны, то тождественно ложен предикат
P ( x) Q ( x) , а поэтому, будут ложны
высказывания
xP(x )
xQ(x) x( P( x) Q( x))
2. Если один из предикатов, например, P(x),
будет не тождественно ложен, то предикат
P ( x) Q ( x) не будет тождественно ложен,
следовательно, истинными будут
высказывания
xP(x )
x( P( x) Q( x))
17.
Решение задачи №53. Если оба предиката P(x) и Q(x) не будут
тождественно ложны, то не будет
P( x) Q( x)
тождественно ложен предикат
Следовательно, будут истинными высказывания
xP(x )
xQ(x)
x( P( x) Q( x))
4. Следовательно, обе части равносильности равны
при любых значениях P(x) и Q(x)
x( P( x) Q( x)) xP( x) xQ( x)
18.
Решение задачи №5ТЛ- тождественно ложный предикат
Не ТЛ – не тождественно ложный предикат
P(x)
Q(x)
P( x) Q( x)
ТЛ
ТЛ
ТЛ
0
0
0
Не ТЛ
ТЛ
Не ТЛ
1
0
1
Не ТЛ
1
1
1
Не ТЛ Не ТЛ
xP(x ) xQ(x) x( P( x) Q( x))
При любых значениях P(x) и Q(x)
x( P( x) Q( x)) xP( x) xQ( x)
19.
Задача № 6Показать
общезначимость
правила обобщения квантора
существования
A( x ) B
правило
xA( x ) B
20.
Решение задачи № 61. Представим правило обобщения квантора в
виде формулы R
R ( A( x ) B ) ( xA( x ) B )
2. Представим импликацию в виде ДНФ
R ( A( x ) B ) ( xA( x ) B )
3. Вынесем квантор из-под знака отрицания
R ( A( x) B ) ( x A( x) B )
21.
Решение задачи № 64. Вынесем квантор из-под скобок по правилу
константы
R ( A( x) B ) x( A( x) B )
5. По правилу вывода, получаем
R Z ( x ) xZ ( x ), где _ Z ( x ) A( x ) B
Так как формула R тождественно истинна в
любой области, значит она общезначима



















 Математика
Математика








