Похожие презентации:
Задачи на построение (7 класс)
1.
Это такие задачи, прирешении которых нужно
построить геометрическую
фигуру,
удовлетворяющую
условию задачи с
помощью циркуля и
линейки без делений
2. Цели:
познакомить учащихся с задачами на построениерассмотреть наиболее простые задачи на построение и научить
учащихся решать их.
формировать умение решать простые задачи на построение
расширить знания об истории геометрии
воспитание ответственного отношения к учебному труду, воли и настойчивости для достижения
конечных результатов при изучении темы
воспитание интереса к истории математики, как науки.
развитие навыков самоконтроля
формирование алгоритмического мышления
3. Из истории математики
В 1672 г. Датский математик Георг Мор, а затем в 1797 г.итальянский учёный Лоренцо Маскерони доказали
независимо один от другого такое утверждение:
всякая задача на построение, разрешимая с
помощью циркуля и линейки, разрешима также
с помощью одного только циркуля. Эти
название построения носят построения Мора Маскерони.
Швейцарский геометр Якоб Штейнер в 1883 г., а
несколько раньше французский математик
Ж.Понселе доказали тоже независимо друг от
друга такое утверждение: любая задача на
построение, разрешимая с помощью циркуля и
линейки, может быть разрешена с помощью
линейки, если только в плоскости чертежа
задана окружность и её центр. Такие
построения носят название построения Понселе
-Штейнера.
4. Зачёт по теме «Окружность»
1. Окружностью называется геометрическаяфигура, которая….
2. Центром окружности является
3. Хордой окружности называется
4. Радиусом окружности называется
5. Диаметром окружности называется
5.
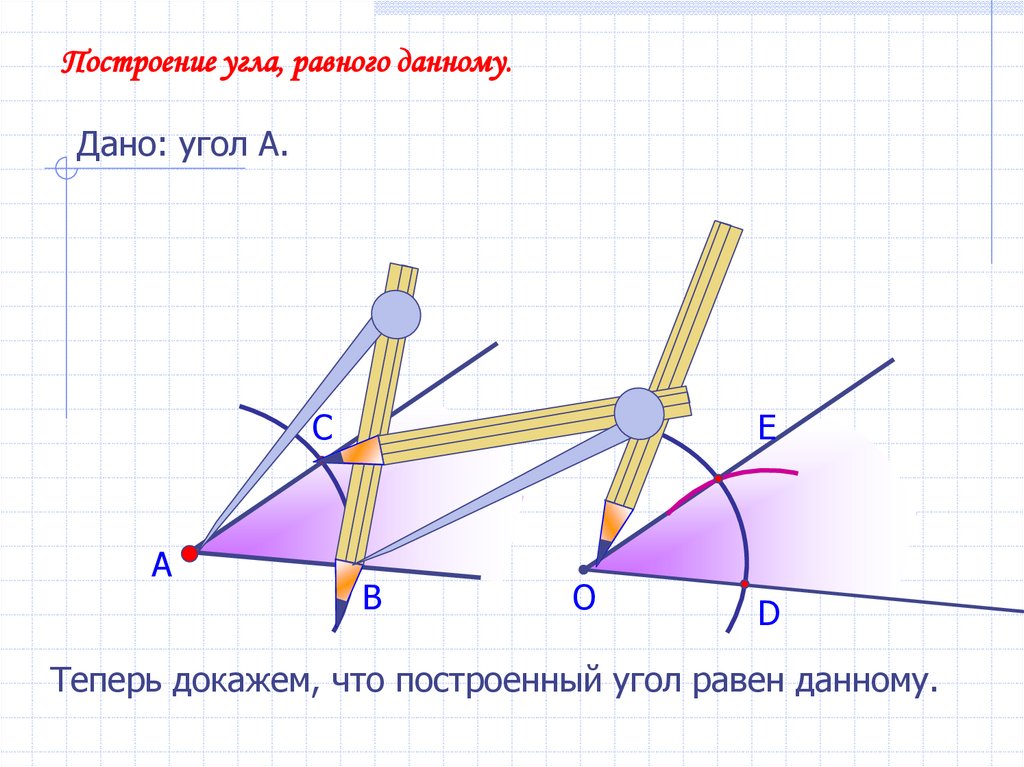
Построение угла, равного данному.Дано: угол А.
С
А
E
В
О
D
Теперь докажем, что построенный угол равен данному.
6.
Построение угла, равного данному.Дано: угол А.
Построили угол О.
С
А
E
В
О
D
Доказать: А = О
Доказательство: рассмотрим треугольники АВС и ОDE.
1. АС=ОЕ, как радиусы одной окружности.
2. АВ=ОD, как радиусы одной окружности.
3. ВС=DE, как радиусы одной окружности.
АВС= ОDЕ (3 приз.) А = О
7.
Построение биссектрисы угла.8.
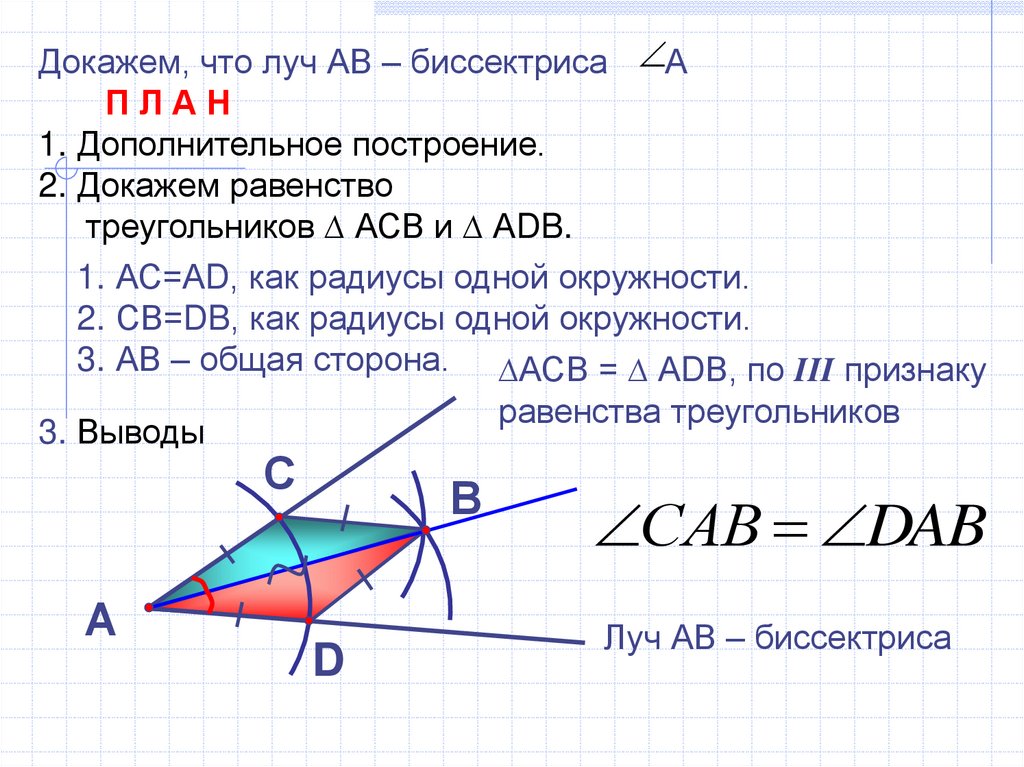
Докажем, что луч АВ – биссектриса АПЛАН
1. Дополнительное построение.
2. Докажем равенство
треугольников ∆ АСВ и ∆ АDB.
1. АС=АD, как радиусы одной окружности.
2. СВ=DB, как радиусы одной окружности.
3. АВ – общая сторона. ∆АСВ = ∆ АDВ, по III признаку
3. Выводы
А
равенства треугольников
С
В
D
САВ DAB
Луч АВ – биссектриса
9.
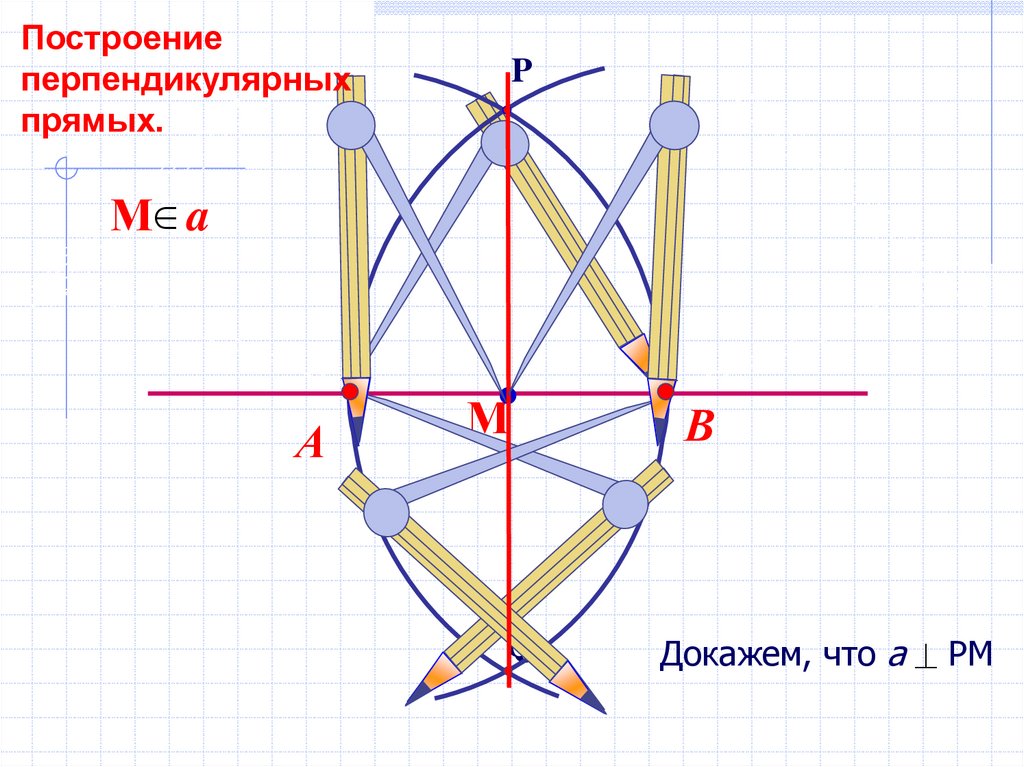
Построениеперпендикулярных
прямых.
P
М a
А
М
Q
В
Докажем, что а РМ
10.
М aP
А
М
В
a
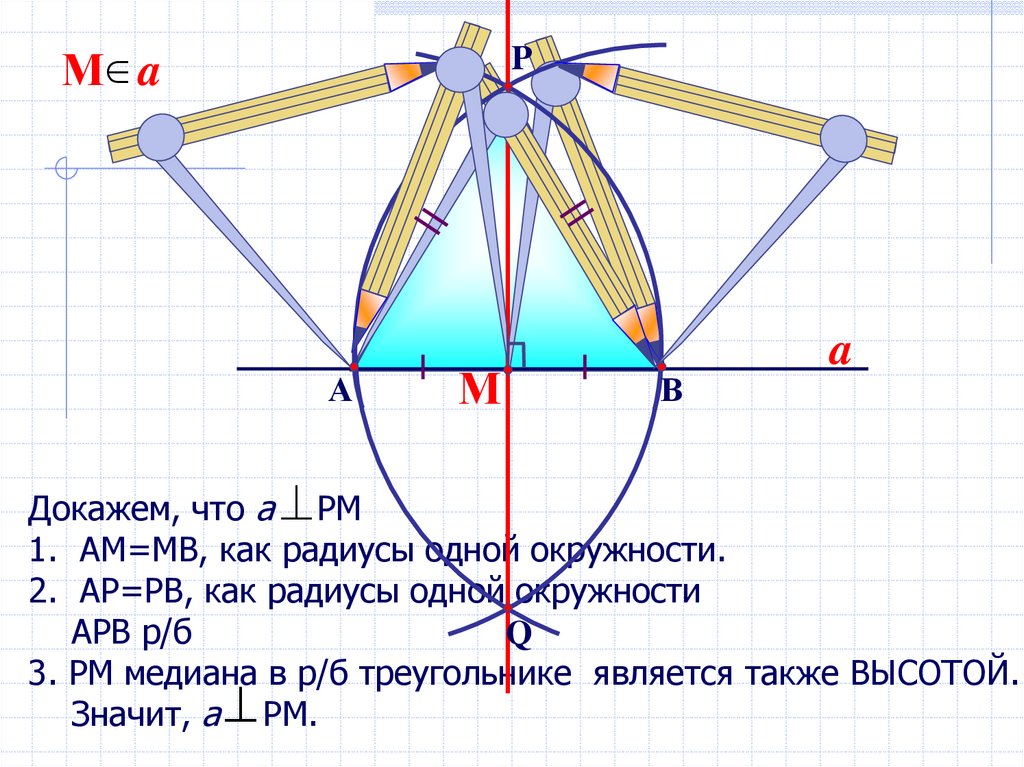
Докажем, что а РМ
1. АМ=МВ, как радиусы одной окружности.
2. АР=РВ, как радиусы одной окружности
АРВ р/б
Q
3. РМ медиана в р/б треугольнике является также ВЫСОТОЙ.
Значит, а РМ.
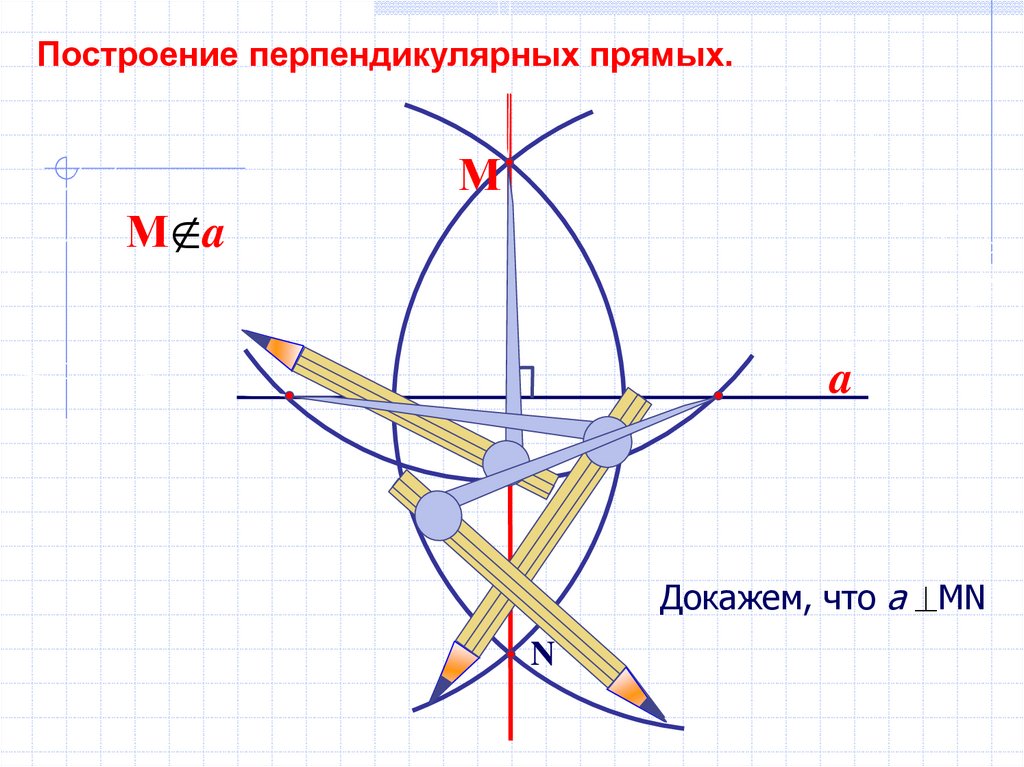
11.
Построение перпендикулярных прямых.М a
М
a
Докажем, что а MN
N
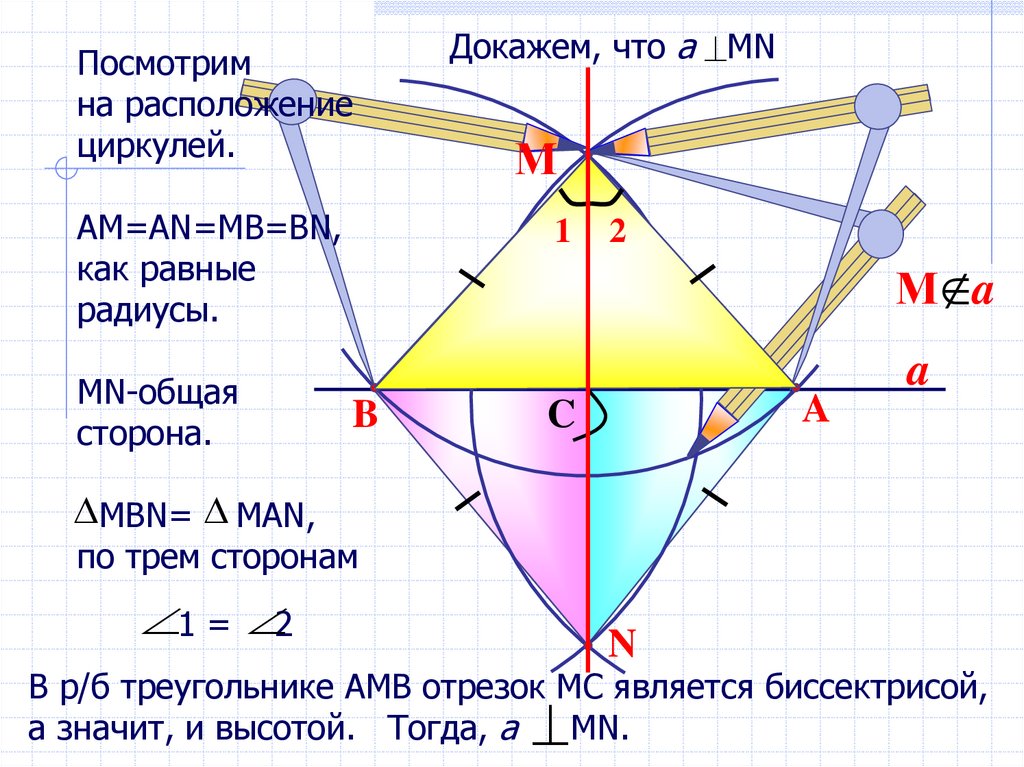
12.
Посмотримна расположение
циркулей.
АМ=АN=MB=BN,
как равные
радиусы.
МN-общая
сторона.
Докажем, что а MN
М
1
B
2
М a
A
C
a
MВN= MAN,
по трем сторонам
1 = 2
N
В р/б треугольнике АМВ отрезок МС является биссектрисой,
а значит, и высотой. Тогда, а
МN.
13.
Построениесередины отрезка
А
P
В
О
Q
Докажем, что О – середина отрезка АВ.
14.
Докажем, что О –середина отрезка АВ.
P
1
АРQ = BPQ,
по трем сторонам.
А
2
О
1 = 2
Треугольник АРВ р/б.
Отрезок РО является биссектрисой,
а значит, и медианой.
Q
Тогда, точка О – середина АВ.
В
15.
Построение треугольника по двумсторонам и углу между ними.
1. Построим луч а.
Дано:
2. Отложим отрезок АВ, равный P1Q1.
3. Построим угол, равный данному.
Отрезки Р1Q1 и Р2Q2
4. Отложим отрезок АС, равный P2Q2.
P1
Q1
P2
Q2
С
h
Угол hk
а
А
D
В
Треугольник АВС искомый. Обоснуй, используя I признак.
k
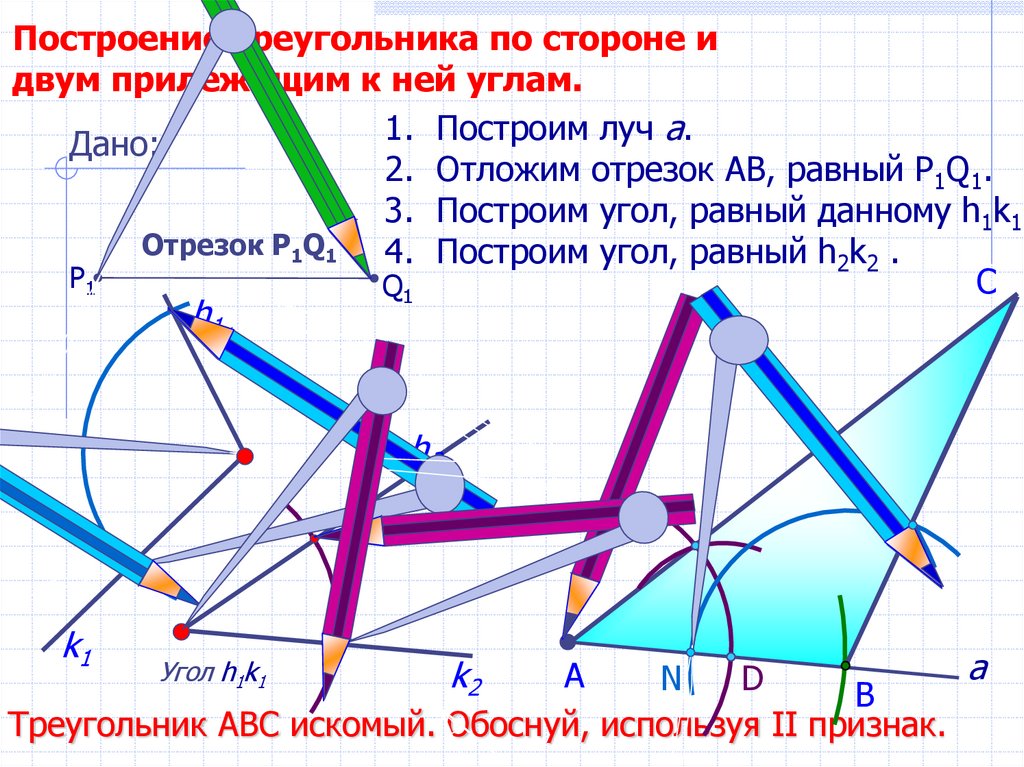
16.
Построение треугольника по стороне идвум прилежащим к ней углам.
1. Построим луч а.
Дано:
2. Отложим отрезок АВ, равный P1Q1.
3. Построим угол, равный данному h1k1.
Отрезок Р1Q1
4. Построим угол, равный h2k2 .
P1
С
Q1
h1
h2
k1
а
А
N
D
В
Треугольник АВС искомый. Обоснуй, используя II признак.
Угол h1k1
k2
17.
Построение треугольника по трем сторонам.Дано:
отрезки
Р1Q1, Р2Q2, P3Q3.
P1
Q1
P2
P3
1. Построим луч а.
2. Отложим отрезок АВ, равный P1Q1.
3. Построим дугу с центром в т. А и
радиусом Р2Q2.
4. Построим дугу с центром в т.В и
радиусом P3Q3.
Q2
С
Q3
А
а
В
Треугольник АВС искомый. Обоснуй, используя III признак.
18. Подведение итогов урока Оцените свою работу, выбрав один из вариантов ответа
Оцените степень сложности урока.Вам было на уроке:
легко
обычно
трудно
Оцените степень вашего усвоения
материала:
усвоил полностью, могу применить
усвоил полностью, но затрудняюсь в применении
усвоил частично
не усвоил.
19. Дома
Параграф 4, пункт 22 учить способыпостроения
№192












 Математика
Математика








