Основы применения ИНС в биотехнических системах «БТСМН»

1.

ОСНОВЫ ПРИМЕНЕНИЯ ИНС В
БИОТЕХНИЧЕСКИХ СИСТЕМАХ
ПРЕЗЕНТАЦИЯ ПО ДИСЦИПЛИНЕ «БТСМН»
Лектор: д.т.н., профессор Истомина Т.В.

2.

ОСНОВНЫЕ ПОНЯТИЯ ИНС
Искусственные нейронные сети (ИНС) — совокупность моделей биологических нейронных
сетей. ИНС представляют собой сеть элементов — искусственных нейронов — связанных между
собой синаптическими соединениями. Сеть обрабатывает входную информацию и в процессе
изменения своего состояния во времени формирует совокупность выходных сигналов.
Искусственные нейронные сети — еще и набор математических и алгоритмических методов для
решения широкого круга задач.
Особенности искусственных нейросетей как универсального инструмента для решения задач.
1) ИНС дают возможность лучше понять организацию нервной системы человека и животных на
средних уровнях: память, обработка сенсорной информации, моторика.
2) ИНС как средство обработки информации:
а) гибкая модель для нелинейной аппроксимации многомерных функций;
б) средство прогнозирования во времени для процессов, зависящих от многих переменных;
в) классификатор по многим признакам, дающий разбиение входного пространства на области;
г) средство распознавания образов;
д) инструмент для поиска по ассоциациям;
е) модель для поиска закономерностей в массивах данных.
3) ИНС свободны от ограничений обычных компьютеров благодаря параллельной обработке и
сильной связанности нейронов.
4) В перспективе ИНС должны помочь нам понять принципы, на которых построены высшие
функции нервной системы: сознание, эмоции, мышление.
2

3.

БИОЛОГИЧЕСКИЙ НЕЙРОН
Центральная нервная система имеет клеточное строение. Единица – нервная клетка, или нейрон. Нейрон имеет следующие
основные свойства.
1. Участвует в обмене веществ и рассеивает энергию, меняет состояние с течением времени, реагирует на входные и формирует
выходные сигналы, - является активной динамической системой.
2. Имеет множество синапсов – контактов для передачи информации.
3. Нейрон взаимодействует путем обмена электрохимическими сигналами двух видов: электротехническими (с затуханием) и
нервными импульсами (спайками) - без затухания.
Существуют два подхода к созданию ИНС. Информационный подход: безразлично, какие механизмы лежат в основе работы
ИНС, важно, чтобы при решении задач информационные процессы в НС были подобны биологическим. Биологический
подход: при моделировании важно полное биоподобие, и необходимо детально изучать работу биологического нейрона.
Биологический нейрон содержит: тело клетки (т) — сома, включая ядро (я),
митохондрии и другие органеллы, поддерживающие жизнедеятельность.
Дендриты (д) – входные волокна, собирают информацию от других нейронов.
Активность в дендритах меняется плавно. Длина их обычно не больше 1 мм.
Мембрана – поддерживает постоянный состав цитоплазмы внутри клетки,
обеспечивает проведение нервных импульсов. Цитоплазма — внутренняя среда
клетки. Отличается концентрацией ионов K+, Na+, Ca++ и других веществ по
сравнению с внеклеточной средой. Аксон (а) – длинное, иногда больше метра,
выходное нервное волокно клетки. Импульс генерируется в аксонном холмике
(а.х.). Аксон обеспечивает проведение импульса и передачу воздействия на
другие нейроны или мышечные волокна (МВ). Ближе к концу аксон часто
ветвится. Синапс (с) – место контакта нервных волокон — передает
возбуждение от клетки к клетке. Передача через синапс почти всегда
однонаправленная. Различают пресинаптические и постсинаптические клетки
— по направлению передачи импульса. Шванновские клетки (шв.кл).
Специфические клетки, почти целиком состоящие из миелина, органического
изолирующего вещества. Плотно "обматывают" нервное волокно 250 слоями
миелина. Неизолированные места нервного волокна между шванновскими
клетками называются перехватами Ранвье (пР). За счет миелиновой изоляции
скорость распространения нервных импульсов возрастает в 5*10 раз и
уменьшаются затраты энергии на проведение импульсов.
3

4.

ИСКУССТВЕННЫЙ НЕЙРОН
Биологический нейрон — сложная система, математическая модель которого до сих пор полностью не
построена. Введено множество моделей, различающихся вычислительной сложностью и сходством с
реальным нейроном. Одна из важнейших — формальный или искусственный нейрон (ФН).
Несмотря на простоту ФН, их сети могут сформировать произвольную многомерную функцию на выходе.
Нейрон состоит из взвешенного сумматора и нелинейного элемента. Функционирование нейрона
определяется формулами:
Нейрон имеет несколько входных сигналов x и один выходной сигнал OUT. Параметрами нейрона,
определяющими его работу, являются: вектор весов w, пороговый уровень θ и вид функции активации F.
4

5.

ОГРАНИЧЕНИЯ МОДЕЛИ НЕЙРОНА
1. Вычисления выхода нейрона предполагаются мгновенными, не вносящими задержки.
Непосредственно моделировать динамические системы, имеющие "внутреннее состояние", с
помощью таких нейронов нельзя.
2. В модели отсутствуют нервные импульсы. Нет модуляции уровня сигнала плотностью
импульсов, как в нервной системе. Не появляются эффекты синхронизации, когда скопления
нейронов обрабатывают информацию синхронно, под управлением периодических волн
возбуждения торможения.
3. Нет четких алгоритмов для выбора функции активации.
4. Нет механизмов, регулирующих работу сети в целом (пример гормональная регуляция
активности в биологических нервных сетях).
5. Чрезмерно формализованы понятия "порог", "весовые коэффициенты". В реальных нейронах
нет числового порога, он динамически меняется в зависимости от активности нейрона и общего
состояния сети. Весовые коэффициенты синапсов тоже не постоянны. "Живые" синапсы обладают
пластичностью и стабильностью: весовые коэффициенты настраиваются в зависимости от
сигналов, проходящих через синапс.
6. Существует большое разнообразие биологических синапсов. Они встречаются в различных
частях клетки и выполняют различные функции. Тормозные и возбуждающие синапсы
реализуются в данной модели в виде весовых коэффициентов противоположного знака, но
разнообразие синапсов этим не ограничивается. Дендродендритные, аксоаксональные синапсы не
реализуются в модели ФН.
7. В модели не прослеживается различие между градуальными потенциалами и нервными
импульсами. Любой сигнал представляется в виде одного числа.
Таким образом, модель формального нейрона не является биоподобной и скорее похожа на
математическую абстракцию, чем на живой нейрон. Тем удивительнее оказывается многообразие
задач, решаемых с помощью таких нейронов и универсальность получаемых алгоритмов.
5

6.

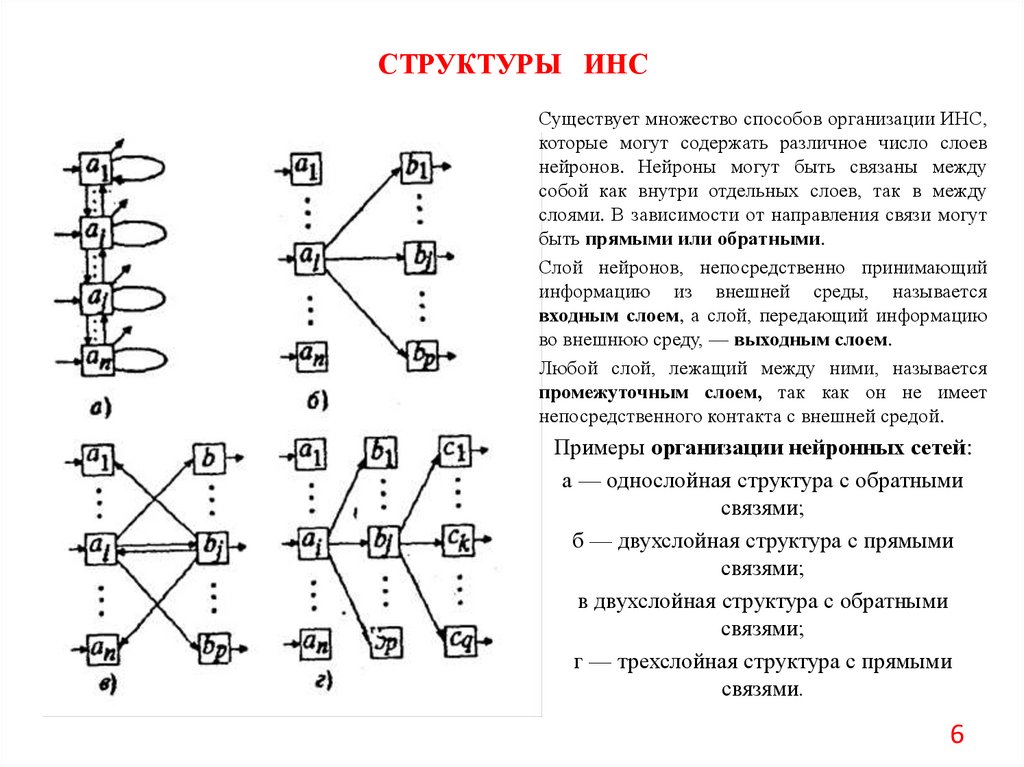
СТРУКТУРЫ ИНС
Существует множество способов организации ИНС,
которые могут содержать различное число слоев
нейронов. Нейроны могут быть связаны между
собой как внутри отдельных слоев, так в между
слоями. В зависимости от направления связи могут
быть прямыми или обратными.
Слой нейронов, непосредственно принимающий
информацию из внешней среды, называется
входным слоем, а слой, передающий информацию
во внешнюю среду, — выходным слоем.
Любой слой, лежащий между ними, называется
промежуточным слоем, так как он не имеет
непосредственного контакта с внешней средой.
Примеры организации нейронных сетей:
а — однослойная структура с обратными
связями;
б — двухслойная структура с прямыми
связями;
в двухслойная структура с обратными
связями;
г — трехслойная структура с прямыми
связями.
6

7.

ОРГАНИЗАЦИЯ ПАМЯТИ В ИНС
Одной из основных характеристик, присущих ИНС, является память.
Отдельные информационные единицы, хранимые в ИНС, называются образами.
Различают два типа памяти: оперативная память (память с произвольной выборкой) и
ассоциативная память.
Оперативная память используется в традиционных ЭВМ последовательного действия и
осуществляет выборку данных по адресам.
Ассоциативная память осуществляет отображение данных в адреса или данных в данные.
В ИНС используется последний тип памяти как наиболее быстродействующий, причем
физически функцию памяти выполняют весовые коэффициенты сети, соответствующие
многочисленным связям между нейронами.
Существуют два механизма отображения данных в памяти ИНС:
автоассоциативный и гетеро-ассоциативный.
В первом случае ИНС хранит лишь образы А1, А2 …, Аn.
Во втором случае сеть хранит пары образов (А1 В1), (А2 В2) ..., (Аn Bn).
Гетероассоциативное отображение можно рассматривать как действие некоторой функции
g, которая, используя матрицу весовых коэффициентов сети W и некоторый входной образ
Аi, извлекает из памяти соответствующую ему пару Вi, т. е. g(Аi,W) = Вi.
Если предъявляемый входной образ А отличен от любою из (А1, А2 …, Аn), то реакция
сети может определяться или принципом ближайшего соседа g(А≈Ai, W) = Bi, или путем
интерполяции g(А=Аi +Δ ,W) = Вi+Δ, выполняемой по всем парам образов (Ai Bi), i=1,…n.
7

8.

ПРИНЦИПЫ ОБУЧЕНИЯ ИНС
Одним из замечательных свойств нейронных сетей является их способность обучаться.
Цель обучения нейронной сети состоит в ее настройке на заданное поведение.
Наиболее распространенным подходом для обучения сети является коннекционизм,
предусматривающий обучение сети путем настройки значений весовых коэффициентов,
соответствующих различным связям между нейронами.
Матрица W весовых коэффициентов wij, сети называется синаптической картой.
Существуют два вида обучения нейронных сетей: обучение с учителем и обучение без учителя.
Обучение с учителем предполагает, что обучение происходит путем предъявления сети готовой
последовательности пар (примеров) (Аi Di), i = 1, …, m образов, называемой обучающей
последовательностью. При этом для каждого входного образа Аi, вычисляется реакция Вi, сети и
сравнивается с соответствующим целевым образом Di. Полученное рассогласование используется
алгоритмом обучения для корректировки синаптической карты таким образом, чтобы уменьшить
ошибку рассогласования. Такая адаптация производится путем циклического предъявления
обучающей выборки до тех пор, пока ошибка рассогласования не достигнет низкого уровня.
В реальности же в процессе обучения наш мозг редко использует данные свыше образы и
постоянно корректирует свое поведение по заданным эталонам. Чаще всего, мозг, используя
поступающую информацию, сам осуществляет ее обобщение в некоторые классы и коррекцию
своей деятельности путем анализа допускаемых ошибок.
В случае обучения без учителя обучающая последовательность состоит лишь из входных образов
Аi. Алгоритм обучения настраивает веса так, чтобы близким входным векторам соответствовали
одинаковые выходные векторы, т. е. фактически осуществляет разбиение пространства входных
образов на классы. При этом до обучения, невозможно предсказать какие именно выходные
образы будут соответствовать классам входных образов. Установить такое соответствие и дать ему
соответствующую интерпретацию оказывается возможным лишь после обучения сети.
8

9.

АЛГОРИТМЫ ОБУЧЕНИЯ ИНС
Обучение нейронной сети можно рассматривать как непрерывный или как дискретный процесс.
В соответствии с этим алгоритмы обучения могут быть описаны либо дифференциальными
уравнениями, либо конечно-разностными.
Использование дифференциальных уравнений предполагает моделирование нейронной сети на
аналоговой технике. Достоинством такого подхода является высокая скорость настройки
нейронной сети. Однако сложность обеспечения коррекции синаптической карты и ограничения
на выбор алгоритма обучения сдерживают использование аналоговых нейронных сетей на
практике. Поэтому в настоящее время нейронные сети реализуются, как правило, на цифровых
элементах с использованием алгоритмов обучения в виде конечно-разностных уравнений.
Физически нейронная сеть может представлять собой специализированный параллельный
процессор или программу, эмулирующую нейронную сеть на последовательной ЭВМ.
У истоков алгоритмов обучения нейронных сетей стоит концепция Хэбба, предложившего
простой алгоритм обучения без учителя, в котором значение веса в соответствую ее связи между
i-м и j-м нейронами, возрастает, если они оба находятся в возбужденном состоянии. В процессе
обучения происходит коррекция весов связей между нейронами в соответствии со степенью
корреляции их состояния, что выражается в виде следующего конечно-разностного уравнения:
где wij(t) и wij(t+1) — значения веса связи нейрона i с нейроном j до настройки (на шаге t) и после
настройки (на шаге t + 1) соответственно; аi(t) — выход нейрона i на шаге t; аj(t) — выход
нейрона j на шаге t; αj — параметр скорости обучения.
9

10.

ЗАДАЧА ЦЕЛЕВОГО ОБУЧЕНИЯ ИНС
Задачу обучения нейронной сети можно рассматривать как за дачу минимизации некоторой
целевой функции:где bi — сигнал на выходе i-го нейрона.
где W — синаптическая карта нейронной сети.
При такой интерпретации для обучения ИНС могут быть использованы различные алгоритмы
нелинейного программирования, такие, как градиентный, квазиньютоновский, случайный
поиск и т. д.
При выборе алгоритма следует учитывать, что для такой задачи оптимизации характерно
большое количество параметров, которое может достигать 100000000 и более, а также
сильная изрезанность оптимизируемой функции и наличие локальных минимумов.
Рациональный выбор целевой функции F(W) и алгоритма для ее минимизации, во многом
определяет успех в обучении сети.
Например, в задаче распознавания образов обучение сети можно проводить следующим
образом. Если имеется m образов, то количество нейронов в выходном слое целесообразно
так же выбрать равным m. Будем считать распознавание i-го образа успешным тогда, когда на
i-м выходном нейроне присутствует 1, а на всех остальных — 0. Тогда в функцию можно
определить так:
где bi — сигнал на выходе i-го нейрона.
10

11.

СТРАТЕГИЯ ЦЕЛЕВОГО ОБУЧЕНИЯ ИНС
Иногда полезно смягчить требования к выходным сигналам сети.
Будем считать, что сеть распознала j-й образ, если сигнал bi, на выходе нейрона i превосходит
сигналы на остальных нейронах. Обозначим через Еi, множество векторов b=[b1, b2 …, bm],
таких, что bi > bj для всех j≠i, а через еi, — m-мерный вектор, у которого i-я координата равна 1
при равенстве 0 всех остальных.
Тогда в качестве целевой функции Fi, можно взять Евклидово расстояние выходного образа сети
до множества Еi,
где — требуемая степень превышения i-го выходного сигнала над остальными.
Наряду с выбором алгоритма обучения не менее важным является стратегия обучения сети.
Хорошим подходом является последовательное обучение сети на серии примеров (Ai Bi), i= 1, 2,
..., m, составляющих обучающую выборку. При этом сеть обучают правильно реагировать сначала
на первый образ А1 за тем на второй А2 и т. д. Однако при данной стратегии возникает опасность
утраты сетью ранее приобретенных навыков при обучении каждому следующему примеру, т. е.
сеть может “забыть” ранее предъявляемые примеры. Для того, чтобы этого не происходило,
необходимо обучать сеть сразу всем примерам из обучающей выборки. В этом случае задача
обучения, строго говоря, становится многокритериальной, так как необходимо одновременно
оптимизировать сразу по нескольким критериям (по каждому примеру). Так как решение такой
задачи сопряжено с большими сложностями, разумной альтернативой является минимизация
целевой функции вида
где — параметры, определяющие требования к качеству обучения сети по каждому из
примеров, такие, что
11

12.

ОБЩИЙ ПРИНЦИП ПОСТРОЕНИЯ
ОПТИМИЗАЦИОННЫХ АЛГОРИТМОВ ОБУЧЕНИЯ ИНС
Общий принцип построения алгоритмов обучения ИНС, основанных на принципах оптимизации,
заключается в следующем.
Для некоторого начального состояния W(0) синаптической карты определяется направление
уменьшения целевой функции и находится ее минимум в этом направлении. При этом
используется один из методов одномерной оптимизации, например, метод золотого сечения,
параболической интерполяции и т. п. Для полученной точки опять находятся направление
убывания функции и осуществляется одномерная оптимизация в данном направления и т. д.
Таким образом, алгоритм обучения имеет вид:
где
и
— направление поиска и величина шага на шаге t алгоритма.
Различные алгоритмы отличаются друг от друга лишь выбором направления поиска.
В частности, для градиентного алгоритма вектор противоположен вектору градиента, т. е.
12

13.

ПЕРСЕПТРОН
Персептрон, являющийся одной из первых попыток создания ИНС, был предложен Розенблатом.
Структура персептрона имеет всего два слоя.
Входной слой Fa обеспечивает прием входных образов Аk= (af, .... а„к), к = 1, ..., т, а выходной слой
Fb состоит из нейронов со ступенчатой функцией активации и обеспечивает формирование
выходных бинарных образов Вк — ( , ..., ), принимающих значения 0 или 1.
Теоретическое доказательство способности персептрона обучиться всему, что он способен
представлять, стимулировало его дальнейшие исследования. В то же время анализ Минского, который показал, что персептрон с одним слоем нейронов способен представлять лишь
ограниченный класс линейно разделимых образов, развеял иллюзии насчет возможностей
персептрона, и работы в данном направлении практически были прекращены (временно!).
13

14.

ПРОБЛЕМА ПЕРСЕПТРОНА
Рассмотрим решение простейшим персептроном задачи дихотомии, т.е. классификации образов
на два класса в случае двух признаков. В этом случае выходной слой персептрона будет состоять
всего лишь из одного нейрона вида
где — выход нейрона; — ступенчатая функция активации; — значение порога.
Предположим также для упрощения, что входные сигналы ai, где i=1,2 – признаки, также
принимают бинарные значения 0 или 1.
В этом случае пространство входных признаков состоит из четырех возможных комбинаций
(0,0); (0,1); (1,0); (1,1) и может быть представлено на плоскости.
В зависимости от конкретных значений весов w1 w2 и порога уравнение
будет определять на плоскости некоторую прямую, разбивающую плоскость признаков на две
части, соответствующие двум классам выходных образов.
14

15.

ПРОБЛЕМА ПЕРСЕПТРОНА
Из приведенного рисунка видно, что возможности персептрона ограничены классом линейно
разделимых образов.
В частности, персептрон не способен реализовать функцию "исключающее ИЛИ", принимающую
значение 0 при равных значениях аргументов и 1 для всех остальных комбинаций.
В этом случае разделяющая прямая должна проходить таким образом, чтобы точки (0,0), (1,1)
находились по одну сторону прямой, а точки (1,0), (0,1) — по другую, что невозможно.
Эти рассуждения останутся справедливыми и в случае наличия произвольного числа признаков
и выходных классов.
Только в этом случае разделяющая функция будет представлять собой гиперплоскость в nмерном пространстве признаков.
15

16.

ОБУЧЕНИЕ ПЕРСЕПТРОНА
Персептрон способен обучаться в классе линейно разделимых функций.
Для обучения персептрона используется процедура обучения с учителем, которая подстраивает
синаптическую карту по ошибкам, измеряемым на выходах нейронной сети.
Алгоритм обучения персептрона состоит из следующих шагов:
1. Начальная инициализация весовых коэффициентов сети и пороговых значений всех нейронов
случайными числами, принимающими значения в интервале [—1,+ l].
2. Для каждого примера (Аk, Вk), k=1, 2, ..., m из обучающей выборки выполняются действия:
2.1. Активация входного слоя Fa вектором Ak,
т.е. i= 1, 2,..., n.
2.2. Вычисление сигналов на выходе нейронов выходного слоя Fb согласно выражению
где ступенчатая функция активации f(x) = 1, если х > О, f(x) = - 1 в противном случае.
2.3. Вычисление ошибки ej между вычисленными выходными величинами bj нейронов и
компонентами желаемого выходного образа Bk обучающей выборки:
2.4. Корректировка весовых коэффициентов согласно соотношению:
где параметр определяет скорость обучения.
2.5.Повторение шага 2 алгоритма, пока ошибки ej, j= I, ..., n не станут достаточно малой величиной
для всех обучающих примеров (Аk,Вk), к= 1, 2, ..., m.
Трудности, связанные с использованием персептрона на практике, состоят в том, что сложно заранее
проверить условие линейной разделимости и предсказать время обучения сети.
Рассмотрим более современные парадигмы нейронных сетей, в которых частично решены указанные
проблемы.
16

17.

РЕШЕНИЕ ПРОБЛЕМЫ ПЕРСЕПТРОНА
Недостаток персептрона, связанный с ограничением представляемых функций классом линейно
разделимых, может быть легко преодолен введением в сеть промежуточных слоев.
Нейронная сеть с одним промежуточным слоем, показанная ниже, способна классифицировать
ограниченные и неограниченные выпуклые области (область называется выпуклой, если отрезок,
соединяющий две любые точки этой области, полностью ей принадлежит).
Рассмотрим возможности нейронной сети с одним промежуточным слоем. Каждый нейрон этого
слоя характеризуется некоторой разделяющей поверхностью в пространстве параметров. Выбирая
соответствующие веса в выходном слое сети, можно образовывать из этих плоскостей различные
выпуклые области, а выбором достаточно большого количества нейронов можно аппроксимировать
многомерные области произвольной формы. Важную роль в возрождении интереса к нейронным
сетям сыграл алгоритм обратного распространения ошибки (backpropagation algorithm), созданный
для обучения нейронных сетей с многослойной структурой, причем количество промежуточных
слоев может быть произвольным. Требования накладываются только на вид функции активации
нейронов, которая должна быть дифференцируема. Обычно используется сигмоидная функция вида
1/(1 + е-x), производная которой имеет простой вид х(1 — х).
17

18.

АЛГОРИТМ ОБРАТНОГО РАСПРОСТРАНЕНИЯ ОШИБКИ
Для того, чтобы понять суть алгоритма, рассмотрим нейронную сеть с одним промежуточным
слоем Fb. Тогда сигналы на выходе нейронов промежуточного слоя и на выходе сети в целом
(на выходе слоя Fc) формируются в соответствии с выражениями
Обучение сети осуществляется с учителем, т. с. сети последовательно предъявляются
обучающие примеры (Ak,Dk), к = 1, 2, ..., m и производится настройка синаптической карты
таким образом, чтобы выходы Сk сети были как можно ближе к заданным образам Dk для
каждой обучающей пары. Сформулируем задачу обучения сети как оптимизационную задачу:
необходимо минимизировать квадрат нормы разности векторов min||Dk-Ck||² .
В случае евклидовой нормы данное выражение может быть записано в виде
Для минимизации данной функции используют градиентный алгоритм поиска. Для этого
предварительно находят производные по параметрам сети, используя правило
дифференцирования сложной функции:
где ошибки слоев ИНС определяются как:
18

19.

АЛГОРИТМ ОБРАТНОГО РАСПРОСТРАНЕНИЯ ОШИБКИ
В процессе обучения сети сначала вычисляются ошибки ej выходного слоя. Затем идет продвижение
вдоль сети в обратном направлении и вычисляются ошибки σj промежуточного слоя. Полученные
ошибки используются для вычисления градиентов для коррекции весовых коэффициентов и пороговых
величин нейронной сети. Суть алгоритма обратного распространения ошибки.
1. Начальная инициализация весовых коэффициентов и пороговых величин случайными числами r:
где Wij - весовой коэффициент, соответствующий связи от i-го нейрона в слое Fb к j-му нейрону в слое
Fc; θr— пороговая величина i-го нейрона слоя Fb; νhi - весовой коэффициент, соответвующий связи от hго входа (слой Fa) к i-му нейрону в слое Fb; ηj — пороговая величина j-го нейрона в слое Fc; r —
случайные числа в диапазоне [—1,1].
2. Для каждой пары (Ak, Dk), k = 1, 2, ..., m из обучающей выборки выполняются следующие действия.
2.1. Активация входного слоя Fa входным, вектором Ak, т. е.
2.2. Вычисление выходных величин нейронов слоя Fb согласно выражению
где S(x) — функция активации вида 1/(1 + е-x).
2.3. Вычисление выходных величин нейронов слоя Fc согласно выражению
2.4. Вычисление ошибки между вычисленными выходными величинами Cj нейронов и компонентами
желаемого выходного вектора Dk обучающей выборки
2.5. Пересчет величины ошибки для всех нейронов слоя Fb выборки:
19

20.

АЛГОРИТМ ОБРАТНОГО РАСПРОСТРАНЕНИЯ ОШИБКИ
2.6. Корректировка весовых коэффициентов и пороговых величин в направлении, противоположном
градиенту, согласно следующим соотношениям:
где параметры α и β определяют скорость обучения.
3. Повторение шага 2 алгоритма до тех пор, пока ошибки еj, j= 1, 2, ..., q не станут достаточно
малыми величинами для всех обучающих примеров (Ak,Dk), к = 1,2, ..., m.
В рассмотренном алгоритме обучение сети примерам (Ak.Dk), k = 1, 2, ..., m осуществляется
последовательно. Как отмечалось ранее, эта стратегия не всегда приводит к успеху, так как при
обучении очередному примеру сеть может "забыть" предыдущие. Этого можно избежать, если
обучать сеть сразу нескольким примерам (странице примеров). Для этого необходимо несколько
модифицировать исходную задачу оптимизации и минимизировать, например, суммарную целевую
функцию вида
В этом случае величины ошибок и градиентов в рассмотренном алгоритме должны вычисляться
путем их суммирования по всем примерам обучающей выборки.
20

21.

ПРОБЛЕМЫ АЛГОРИТМА
ОБРАТНОГО РАСПРОСТРАНЕНИЯ ОШИБКИ
Несмотря на широкое использование алгоритма обратного распространения ошибки, он не лишен
недостатков. Прежде всего, это длительное время обучения. Более того, в случае сложных задач он
вообще может не привести к успеху.
Такая ситуация возникает в основном по двум причинам: паралич сети и попадание в ловушку
локального минимума.
Паралич сети возникает в том случае, когда все нейроны функционируют на грани насыщения, т. е.
при очень больших значениях выхода. В этом случае производная функции активации очень мала.
А так как изменения параметров сети в процессе обучения пропорциональны этой производной,
обучение практически может прекратиться.
Этого можно избежать уменьшением размеров α и β шага обучения, что, однако, увеличивает время
обучения.
Другой опасностью является попадание в локальный минимум.
Поверхность целевой функции F нейронной сети имеет, как правило, изрезанный вид и
характеризуется наличием локальных минимумов, при попадании в которые вектор градиента
близок к нулю. Поэтому при попадании в локальный минимум процесс обучения с использованием
градиентного алгоритма поиска прекращается. В этом случае сеть недоучивается, а ее синаптическая
карта не будет являться оптимальной.
Для предотвращения "зависания" сети в локальных минимумах могут быть использованы
стохастические методы обучения нейронных сетей.
21

22.

СТОХАСТИЧЕСКИЕ АЛГОРИТМЫ ОБУЧЕНИЯ
Основной причиной использования стохастических алгоритмов для обучения нейронных сетей является их
способность находить глобальный минимум целевой функции. Суть стохастического подхода заключается в
изменении весовых коэффициентов сети случайным образом и сохранении тех изменений, которые ведут к
уменьшению заданной целевой функции. Основным вопросом при построении стохастических алгоритмов
является рациональное изменение величины случайных приращений таким образом, чтобы алгоритм мог
выбираться из "ловушек", образованных локальными минимумами. Чтобы продемонстрировать эту ситуацию,
рассмотрим некоторую условную целевую функцию, показанную ниже.
Если в процессе поиска параметры сети оказались в точке А локального минимума и величина шага является
достаточно малой, то случайные шаги в любом направлении не приведут к уменьшению целевой функции и. будут
отвергнуты. В этом случае точка В глобального минимума никогда не будет достигнута. Если же значения
случайных приращений большие, то в процессе поиска будут посещаться как окрестности точки А, так и точки В.
Однако слишком большие флюктуации не позволят поиску стабилизироваться в точке В глобального минимума.
Подходящая стратегия могла бы состоять в постепенном уменьшении величины шага, что позволило бы избежать
локальных минимумов и в то же время стабилизировать поиск в точке глобального минимума.
В этой связи полезно провести аналогию с шариком, находящимся на холмистой поверхности. Если
поверхность заставить случайно колебаться в горизонтальном направлении, то шарик будет перекатываться из
одного углубления (локального минимума) в другое. При уменьшении амплитуды таких колебаний шарик будет на
некоторое время оставаться как в точке А, так и в точке В. Однако наступит такой момент, что сила колебаний будет
достаточной, чтобы вывести шарик из точки А, но уже недостаточной, чтобы вывести его из точки В. Дальнейшее
уменьшение колебаний поверхности заставит шарик стабилизироваться в точке В глобального минимума.
22

23.

СТОХАСТИЧЕСКИЕ АЛГОРИТМЫ ОБУЧЕНИЯ
Стохастическое обучение нейронных сетей по существу представляет собой тот же самый процесс. В начале обучения
производятся достаточно большие случайные коррекции, которые затем постепенно уменьшаются. При этом для
исключения "зависания” алгоритма в локальных минимумах должны сохраняться не только те изменения
синаптической карты, которые ведут к уменьшению целевой функции, но также изредка и изменения, приводящие к
ее увеличению. Такое обучение позволяет, сети в конце концов стабилизироваться в точке глобального минимума.
Основным вопросом при построении стохастических алгоритмов обучения является детальная разработка такой
стратегии изменения синаптической карты. Здесь полезной оказывается аналогия с физическими процессами,
происходящими при отжиге металла. В расплавленном металле атомы находятся в беспорядочном движении. При
понижении температуры атомы стремятся к состоянию энергетического минимума (кристаллизации), т. е., к
глобальному минимуму. В процессе отжига энергетическое состояние металла описывается распределением
где Р(Е) — плотность распределения энергии Е металла; k — постоянная Больцмана; Т — температура Кельвина.
В соответствии с данной формулой при высокой температуре вероятность всех энергетических состояний металла
одинакова. По мере снижения температуры вероятность высокоэнергетических состояний уменьшается по сравнению с
низкоэнергетическими, и при стремлении ее к 0 вероятность низкоэнергетического стояния приближается к 1.
По аналогии с процессом отжига металлов можно ввести некоторую искусственную температуру. Уменьшая ее в
процессе обучения, будем сохранять состояния сети, связанные с увеличением целевой функции, в соответствии с
распределением Больцмана. Таким образом, по мере обучения шаги в сторону увеличения целевой функции будут
делаться все реже и реже. Одновременно с этим по некоторому правилу мы будем также уменьшать величину
случайного шага. В качестве такого правила, например, может быть использовано распределение Гаусса, в соответствии
с которым при увеличении искусственной температуры вероятность больших шагов будет уменьшаться.
К важным факторам, влияющим на сходимость алгоритма к глобальному минимуму, следует отнести также скорость
изменения искусственной температуры. Очевидно, что уменьшая ее слишком быстро, мы рискуем не достичь точки
глобального минимума. Проведенные теоретические исследования данного вопроса показали, что "охлаждение" сети
должно быть обратно пропорционально логарифму времени, т. е. искусственная температура должна изменяться как:
где T(t) — искусственная температура на шаге t алгоритма; T0 — начальная температура.
23

24.

СТОХАСИЧЕСКАЯ ИНС «МАШИНА БОЛЬЦМАНА»
Нейронная сеть, основанная на рассмотренных принципах стохастического обучения, называется
машиной Больцмана и функционирует согласно следующему алгоритму.
1. Начальная инициализация синаптической карты W нейронной сети случайными числами r.
Положить t=1 и выбрать начальное значение T0 искусственной температуры достаточно большим.
2. Активизация входного слоя сети, вычисление ее реакции и значения целевой функции F(W).
3. Вычисление искусственной температуры T= To/(1 + logt).
4. Генерирование случайных приращений весов, распределенных по закону Гаусса Р(α) = ехр(-α2/T2), и
вычисление скорректированной синаптической карты W*.
5. Активизация входного слоя сети, вычисление ее реакции и значения целевой функции F(W*) для новой
синаптической карты. Если ΔF= F(W*) - F(W) ≤ 0, то сохранить изменение синаптической карты.
Если ΔF > 0, то сгенерировать случайное число ξ, равновероятно принимающее значение в интервале [0,1],
и в случае ξ < ехр (ΔF /T) сохранить изменения в синаптической карте, иначе вернуться к прежней.
6. Повторение шагов 3—5 алгоритма до тех пор, пока значение целевой функции не станет меньше
некоторого предела при достаточно низкой искусственной температуре.
Хотя данный стохастический алгоритм и позволяет достичь точки глобального минимума, время обучения
сети по сравнению с алгоритмом обратного распространения ошибки возрастает. Это связано с
выполнением большого числа случайных шагов в направлении возрастания целевой функции. Известен
ряд приемов, позволяющих сократить время обучения сети.
Один из способов использует понятие искусственной теплоемкости сети, т. к. в процессе отжига металла
наблюдаются резкие изменения уровня энергии, сопровождающиеся скачкообразным изменением
теплоемкости - свойства, характеризующего скорость изменения температуры в зависимости от энергии.
В ИНС происходят аналогичные явления. При "критических" температурах небольшое ее изменение
приводит к резкому уменьшению целевой функции, т. е. искусственная теплоемкость резко падает.
При таких температурах скорость ее изменения должна замедляться, чтобы гарантировать сходимость к
глобальному минимуму. В остальном диапазоне температур может быть без риска использована более
высокая скорость снижения температуры, что приводит к существенному уменьшению времени обучения.
24

25.

АЛГОРИТМ ВСТРЕЧНОГО РАСПРОСТРАНЕНИЯ ОШИБКИ
В отличие от алгоритма обратного распространения ошибки алгоритм встречного распространения ошибки
(counterpopagation) не является столь общим, однако позволяет существенно уменьшить время обучения нейронной
сети. Это оказывается полезным в тех случаях, когда имеются ограничения на длительность обучения.
Данный алгоритм объединяет две нейросетевые парадигмы: самоорганизующуюся карту Кохонена и сеть
Гроссберга. Такое объединение оказалось весьма полезным и позволило достигнуть новых свойств, которых нет ни у
одной из них по отдельности. Комбинирование различных нейронных сетей позволяет построить модели, белее
близкие к мозгу по архитектуре, которая представляет собой, каскадные соединения нейронов различных типов.
Структура сети встречного распространения ошибки аналогична рассмотренной выше и содержит два слоя нейронов:
слой Fb — слой нейронов Кохонена с весами vhi,, и Fc — слой нейронов Гросберга с весами wij.
Слой Fa не содержит нейронов и служит просто для приема входных сигналов.
В процессе обучения сети предъявляются обучающие примеры (Ak, Dk), к = 1, ..., m. Эти образы могут быть
двоичными, т. е. состоять из 0 и 1, или непрерывными. При предъявлении на вход обученной сети входного образа Аk
на выходе сети формируется ассоциированный с ним выходной образ Dk. Уже в процессе обучения сеть приобретает
способность к обобщению, т.е. дает правильный выход при предъявлении сети неполного или искаженного образа.
Рассмотрим более подробно процедуру обучения различных слоев сети.
Обучение слоя Кохонена осуществляется без учителя по принципу "победитель забирает все", т. е. для заданного
входного образа активизируется лишь один нейрон слоя Fb, имеющий максимальный выходной сигнал. Таким
образом, слой Кохонена фактически осуществляет классификацию входных образов на группы схожих.
Предварительно входные образы желательно нормализовать по формуле
Эта операция превращает входной вектор в единичный вектор с тем же самым направлением.
В процессе обучения на входы нейронов слоя Кохонена подается нормализованный входной образ Аnk'. Нейрон с
максимальным выходным сигналом (допустим, j-й нейрон) объявляется победителем, и его синаптические
коэффициенты подстраиваются по алгоритму
Здесь параметр α(t)определяет скорость обучения и обычно постепенно уменьшается в процессе обучения.
25

26.

АЛГОРИТМ ВСТРЕЧНОГО РАСПРОСТРАНЕНИЯ ОШИБКИ
В соответствии с данным алгоритмом коррекция вектора весов нейрона-победителя осуществляется в направлении,
уменьшающем разность между этим вектором и входным образом. Это наглядно демонстрируется на рисунке, из
которого видно, что в процессе обучения происходит вращение вектора Vj=[v1j…vnj] весовых коэффициентов в
направлении входного образа Аk'.
При этом величина коррекции определяется параметром α алгоритма. Если бы каждому входному образу
соответствовал свой нейрон Кохонена, то, выбрав параметр α = 1, можно было бы обучить весь слой, выполняя всего
лишь одну коррекцию на каждый нейрон. На практике, как правило, обучающее множество включает в себя группы
сходных между собой входных векторов. Нейронная сеть должна быть обучена активизировать один и тот же нейрон
для близких входных векторов в группе. Это достигается уменьшением параметра α алгоритма в процессе обучения.
В результате синаптические веса нейрона, ассоциированные с некоторой группой близких входных образов, будут
стабилизироваться вблизи среднего значения, соответствующего "центру" данной группы.
Для обучения слоя Гросберга может быть использован ранее рассмотренный алгоритм обучения с учителем вида
где еj — ошибка j-го выхода, равная разности между j-й компо¬нентой желаемого образа и выходом j-го нейрона слоя
Гросберга, т. е. (djk — cj ); β(t) — параметр, определяющий скорость обучения. Для обеспечения сходимости
алгоритма параметр β(t) должен выбираться небольшим (порядка 0,1) и постепенно уменьшаться в процессе
обучения.
Таким образом, в процессе обучения нейронной сети в целом синаптические веса в слое Кохонена корректируются по
значениям входных образов Аk, в то время как веса в слое Гросберга корректируются по значениям выходных образов
Dk. В результате обучения слоя Кохонена происходит автоассоциативная классификация входных образов, которая
далее используется в слое Гросберга для получения на выходе сети заданных выходных образов.
26

27.

АЛГОРИТМ ВСТРЕЧНОГО РАСПРОСТРАНЕНИЯ ОШИБКИ
Базовый алгоритм обратного распространения ошибки можно представить состоящим из следующих шагов.
1. Начальная инициализация всех весовых коэффициентов нейронов слоя Кохонена (Fb) случайными числами r,
принимающими значения в интервале [0,1]:
2. Формирование р нормализованных векторов Vj’=[v1j’…vnj’] синаптических коэффициентов, соответствующих
нейронам слоя Кохонена:
где ||Vj|| — евклидова норма вектора Vj=[v1j…vnj] .
3. Для каждой пары (Аk, Dk), k = 1,2, .... m из обучающей выборки выполняется следующая последовательность
действий.
3.1. Нормализация всех входных образов Аk = [а1k... аnk] к векторам единичной длины
3.2. Нахождение среди векторов Vi', где i= 1, 2, ..., р вектора Vg', наиболее близкого к Аk в смысле минимума
евклидова расстояния, т. е.
3.3. Корректировка синаптических весов vhg слоя Кохонена в направлении входного образа Аk по алгоритму
где параметр α(t) скорости обучения уменьшается в процессе обучения по закону 1/t или 0,2[1 - t/10000].
3.4. Нормализация скорректированною вектора весов к вектору единичной длины
27

28.

АЛГОРИТМ ВСТРЕЧНОГО РАСПРОСТРАНЕНИЯ ОШИБКИ
3.5. Вычисление выходных величин нейронов слоя Fb Кохонена
3.6. Вычисление выходных величин нейронов слоя Fc Гросcберга согласно выражению
3.7. Определение ошибки между вычисленными выходными величинами cj нейронов и компонентами
желаемого выходного вектора Dk обучающей выборки
3.8. Корректировка синаптических весов wgJ нейронов слоя Fb Гросберга по формуле
4. Повторение шага 3 алгоритма до тех пор, пока ошибки еj, j = 1, 2, ..., q не станут достаточно малыми
величинами для всех обучающих примеров (Аk , Dk ), к — 1, 2, ..., т.
В базовом алгоритме для начальной инициализации сети используется стандартный прием, состоящий в
присваивании всем весовым коэффициентам слоя Кохонена случайных значений.
После такой начальной инициализации векторы синаптических весов нейронов будут распределяться
равномерно по поверхности гиперсферы единичного радиуса. В то же время входные векторы (образы), как
правило, распределены неравномерно и могут быть сосредоточены на относительно малой части
поверхности гиперсферы. Это может привести к тому, что часть весовых векторов будет так удалена от
любого входного вектора, что никогда не приблизится к ним, т. е. будет всегда иметь нулевой выход и фактически окажется бесполезной. Оставшихся же векторов может оказаться слишком мало, чтобы
разделить входные образы на классы, которые могут быть слишком близко расположены друг к другу.
28

29.

МЕТОДЫ УЛУЧШЕНИЯ АЛГОРИТМА ВРО
Более эффективным решением, очевидно, является начальное распределение весовых векторов в соответствии с плотностью распределения входных образов. Один из методов, основанный на этом принципе,
известен под названием метода выпуклой комбинации и состоит в следующем.
Все веса приравниваются к одной и той же величине п-1/2 (где п — размерность входных образов), т. е.
совпадают и имеют единичную длину.
Компонентам входных векторов Ак присваиваются значения β(t)
ahk' + (1 — β(t)) п-1/2.
В начале обучения β очень мало и входные векторы почти совпадают с весовыми векторами.
В ходе обучения сети параметр β постепенно возрастает, приближаясь к 1, и входные образы стремятся к
Аk'. Таким образом, векторы синаптических весов отслеживают один или небольшую группу близких
входных векторов, постепенно приближающихся к своим истинным значениям. Хотя метод выпуклой
комбинации и позволяет достичь требуемой цели, однако время обучения возрастает, так как весовые
коэффициенты подстраиваются к изменяющимся входным образам.
Модификация данного метода, позволяющая сократить время обучения, состоит в том, что на начальной
стадии обучения подстраиваются все веса, а не только веса, связанные с выигравшим нейроном.
По мере обучения коррекция весов начинает производиться лишь в некоторой окрестности победившего
нейрона, радиус которой постепенно уменьшается.
Метод функционирования нейронной сети, когда в конечном итоге активизируется лишь один нейрон слоя
Кохонена, называется методом аккредитации. Так как на выходе всех остальных нейронов присутствует
нулевой сигнал, на выходе слоя Гроссберга в этом случае формируется вектор, равный весам связей,
идущих от единственного возбужденного нейрона.
Известен также более общий метод интерполяции, когда активизируется целая группа нейронов,
имеющих наибольшие значения выходов. В этом случае вектор выходов нейронов группы предварительно
нормализуется и используется далее для вычисления выходов нейронов Гроссберга. Так как реализуемая
при том функциональная зависимость существенно более сложная, чем в методе аккредитации, то данный
метод позволяет реализовать более сложные ассоциации образов.
29

30.

ИНС С ОБРАТНЫМИ СВЯЗЯМИ
Ранее рассматривались сети, в которых сигналы распространялись в прямом направлении, т. е. без
обратных связей. Такие сети всегда устойчивы!
В нейронных сетях с обратными связями допускается передача выходных сигналов на вход сети.
Это приводит к переходным процессам в сети, после которых сеть может установиться в некоторое
устойчивое состояние. Однако возможна также и ситуация, при которой в сети никогда не наступит
состояние равновесия. В этом случае сеть является неустойчивой.
Анализ устойчивости нейронных сетей с обратными связями представляет собой сложную теоретическую
задачу. Ограничимся рассмотрением подкласса нейронных сетей с обратными связями, устойчивость
которых при определенных условиях может быть доказана. Примером является сеть Хопфильда.
Эта простая сеть представляет собой один слой нейронов.
Сигнал на выходе
каждого нейрона формируется согласно
выражению
где аj(t) — выход нейрона j на такте t, F(x) — ступенчатая пороговая
функция, принимающая значения ±1.
Данное уравнение может быть также переписано в матричном виде
следующим образом:
30

31.

МОДЕЛИ АССОЦИАТИВНОЙ ПАМЯТИ
Сеть Хопфильда - примитивная модель ассоциативной памяти, позволяющая по искаженному входному образу извлечь
ближайший к нему эталон.
Для этого сеть должна быть предварительно обучена на некоторой обучающей выборке.
Обучение ведется без учителя путем предъявления сети входных образов Аk; к = 1, ..., т.
Предъявляемые образы запоминаются в синаптической карте, которая формируется следующим образом.
Это выражение фактически является матричной формой записи алгоритма обучения Хэбба, согласно которому
синаптические веса формируются путем вычисления корреляций между состояниями отдельных нейронов.
Такое задание весов позволяет сети запомнить входные образы и обеспечить в дальнейшем возможность их извлечения по
неполным и искаженным данным.
В процессе функционирования нейроны обученной сети активизируются некоторым входным образом, а затем сети
предоставляется возможность "расслабиться", опустившись в ближайший энергетический минимум. Теоретически было
показано, что сеть всегда достигнет устойчивого состояния, если синаптическая карта симметрична и ее диагональные
элементы равны нулю, т. е. wij=wji, wii = 0.
Алгоритм функционирования сети Хопфильда состоит из следующих шагов.
1.Формирование синаптической карты сети W путем ее обучения по серии входных образов Аk = [a1k, ..., аn к], к = 1, ..., m.
Здесь единичная матрица I введена, чтобы обеспечить равенство нулю диагональных элементов синаптической карты wii=0.
2.Начальная активация сети входным образом С = [с1, ..., сn],т. е. приведение нейронов сети в состояния: aj= cj, j = 1, ..., п.
3.Итерационное вычисление выходных сигналов сети до тех пор, пока сеть не достигает установившегося состояния.
Таким образом, двунаправленная ассоциативная память обладает способностью к исправлению и обобщению.
Если искаженный или незавершенный образ подаются на вход сети, то он тем не менее, способна выдать запомненный
ранее выходной образ, который, в свою очередь, стремится восстановить входной образ. Это может потребовать нескольких
итераций, но, как правило, их количество не слишком большое, и сеть всегда является устойчивой.
Устойчивость сети обеспечивается тем обстоятельством, что синаптическая карта в обратных связях сети выбирается равной
транспонированной карте в прямых связях сети.
Аналогично сети Хопфильда для двунаправленной ассоциативной памяти также имеется ограничение на количество образов.
Если это ограничение не выполняется, то сеть может выдавать неверные ассоциации. Для запоминания т ассоциаций
количество нейронов N в наименьшем слое должно выбираться таким образом, чтобы выполнялось неравенство т <
N/(21og2N). Например, сеть с 1024 нейронами может запомнить не более 25 ассоциаций.
31

32.

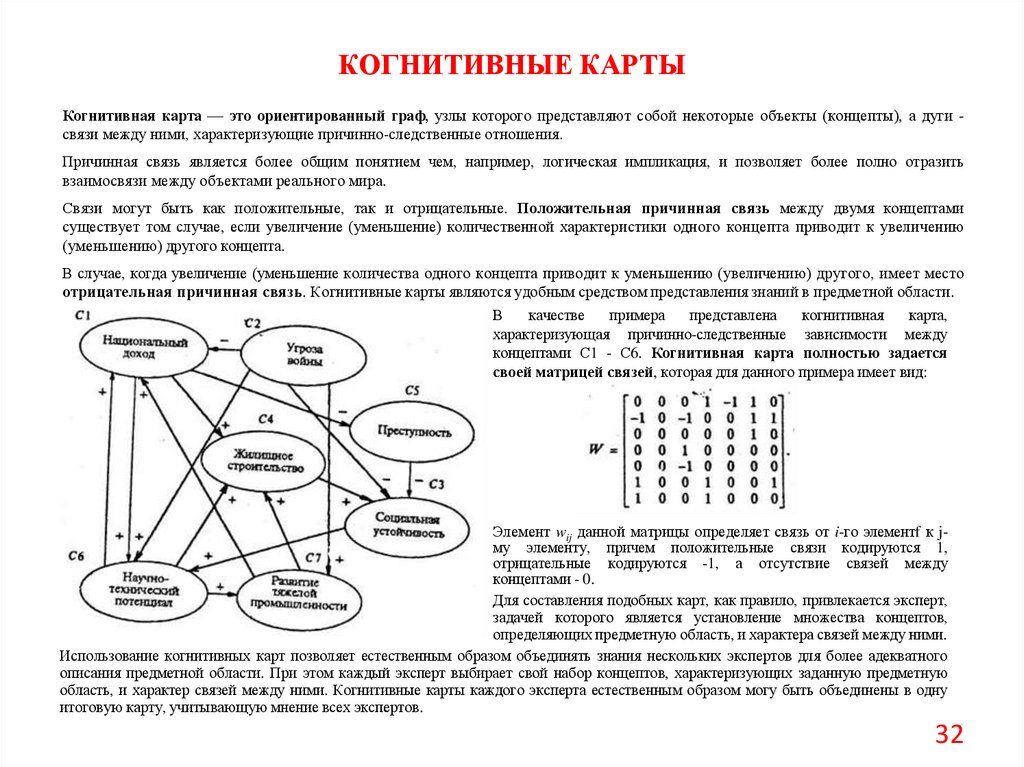
КОГНИТИВНЫЕ КАРТЫ
Когнитивная карта — это ориентированный граф, узлы которого представляют собой некоторые объекты (концепты), а дуги связи между ними, характеризующие причинно-следственные отношения.
Причинная связь является более общим понятием чем, например, логическая импликация, и позволяет более полно отразить
взаимосвязи между объектами реального мира.
Связи могут быть как положительные, так и отрицательные. Положительная причинная связь между двумя концептами
существует том случае, если увеличение (уменьшение) количественной характеристики одного концепта приводит к увеличению
(уменьшению) другого концепта.
В случае, когда увеличение (уменьшение количества одного концепта приводит к уменьшению (увеличению) другого, имеет место
отрицательная причинная связь. Когнитивные карты являются удобным средством представления знаний в предметной области.
В
качестве
примера
представлена
когнитивная
карта,
характеризующая причинно-следственные зависимости между
концептами С1 - С6. Когнитивная карта полностью задается
своей матрицей связей, которая для данного примера имеет вид:
Элемент wij данной матрицы определяет связь от i-го элементf к jму элементу, причем положительные связи кодируются 1,
отрицательные кодируются -1, а отсутствие связей между
концептами - 0.
Для составления подобных карт, как правило, привлекается эксперт,
задачей которого является установление множества концептов,
определяющих предметную область, и характера связей между ними.
Использование когнитивных карт позволяет естественным образом объединять знания нескольких экспертов для более адекватного
описания предметной области. При этом каждый эксперт выбирает свой набор концептов, характеризующих заданную предметную
область, и характер связей между ними. Когнитивные карты каждого эксперта естественным образом могу быть объединены в одну
итоговую карту, учитывающую мнение всех экспертов.
32

33.

СПАСИБО ЗА ВНИМАНИЕ!
33