Похожие презентации:
Уравнение Вейса – Лапика
1.
Уравнение Вейса – Лапикаa
I b
τи
IП – пороговое значение постоянного тока,
приводящее к возбуждению данной ткани
(мышечной или нервной)
τи – время воздействия
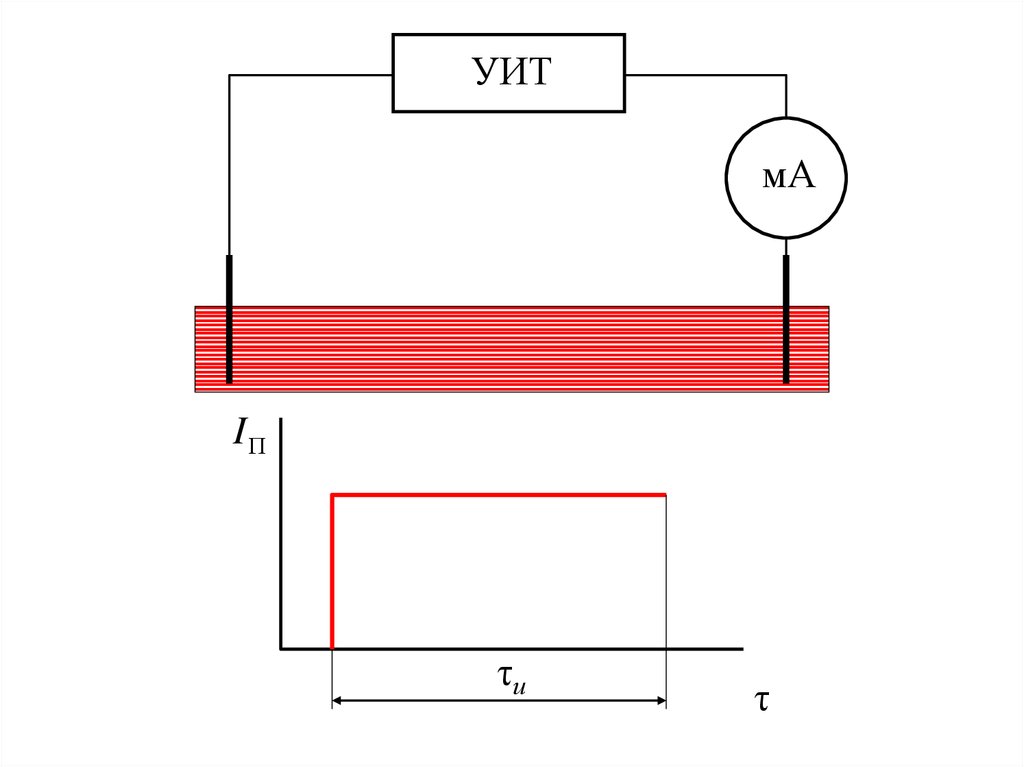
2.
УИТмА
I
τи
τ
3.
aI b
τи
Характеристика
возбуждения
данной мышцы
(гипербола В – Л)
I
2R
-
+
и
I const R b
chr
τи
R – горизонтальная асимптота гиперболы В – Л
chr = τи при IП = 2R
4.
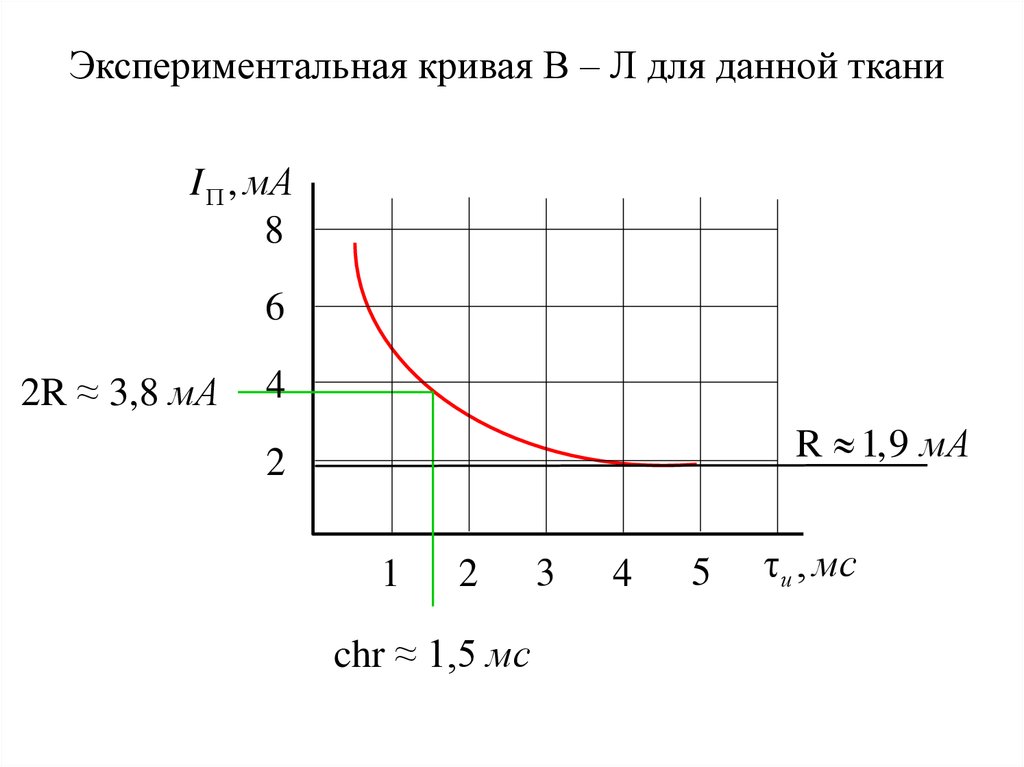
Экспериментальная кривая В – Л для данной тканиI , мА
8
6
2R ≈ 3,8 мА
4
R 1,9 мА
2
1
2
chr ≈ 1,5 мс
3
4
5
τи , мс
5.
I , мА8
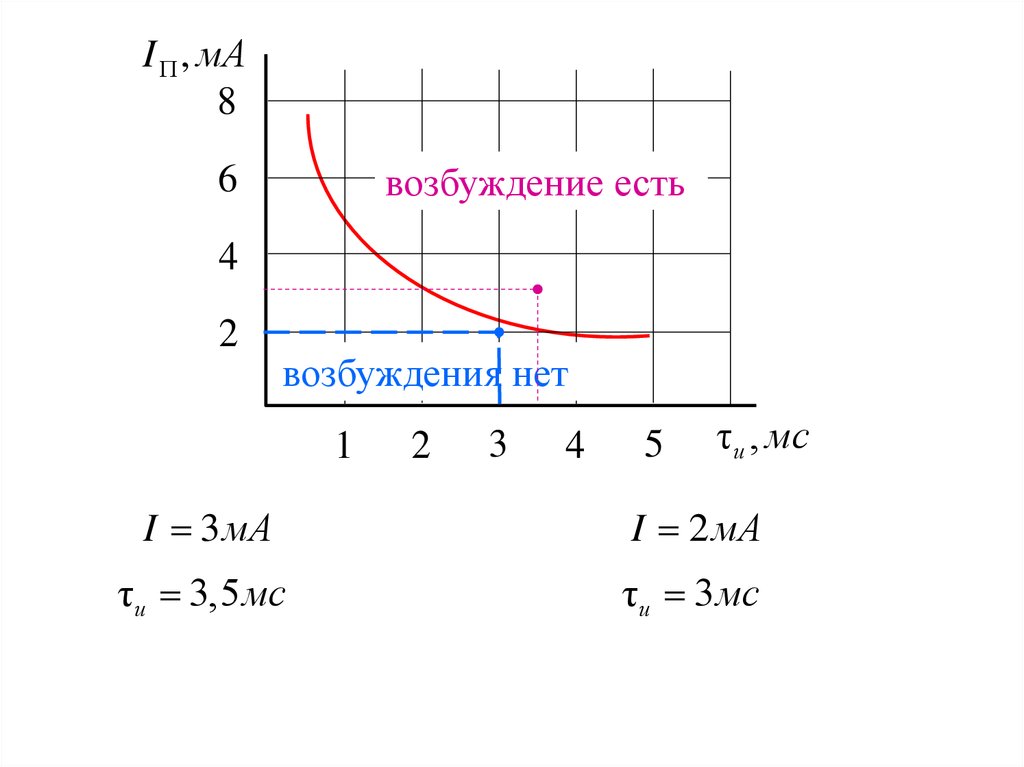
возбуждение есть
6
4
2
возбуждения нет
1
2
3
4
5
τи , мс
I 3 мА
I 2 мА
τи 3,5 мс
τи 3 мс
6.
a 10 мА сb 2,5 мА
a
10
I b 2,5 , мА
τи
τи
R 2,5 мА
2R 5 мА
a
10
2R
b
2,5 5
chr
chr
chr 4 мс
7.
Определить наличие или отсутствие реакции:I , τи
Для данного τи определяется IП:
a
10
I b 2,5 , мА
τи
τи
Если: I ≥ IП → возбуждение есть;
если: I < IП → возбуждения нет
I 6 мА, τи 4 мс
I 4 мА, τи 5 мс
8.
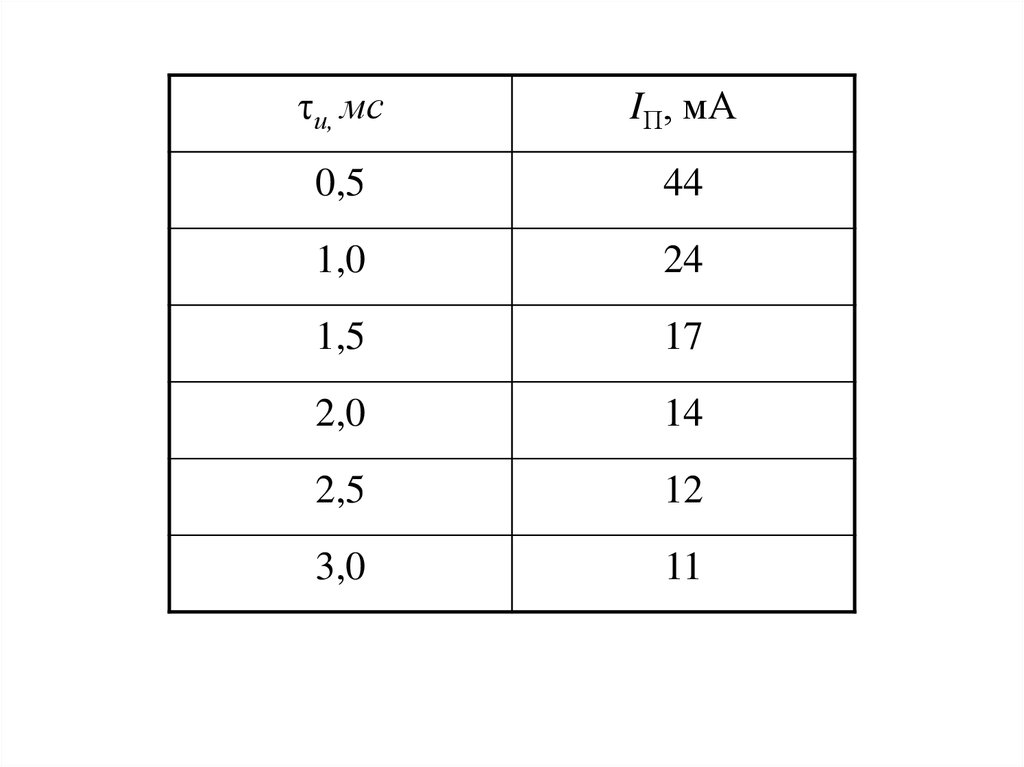
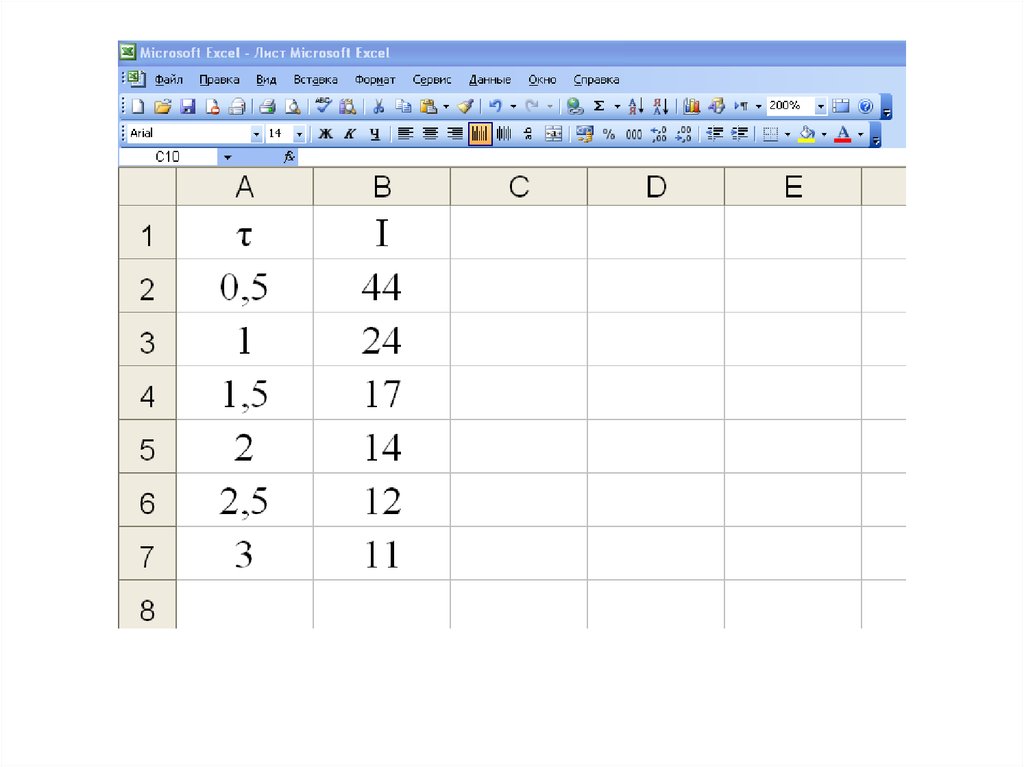
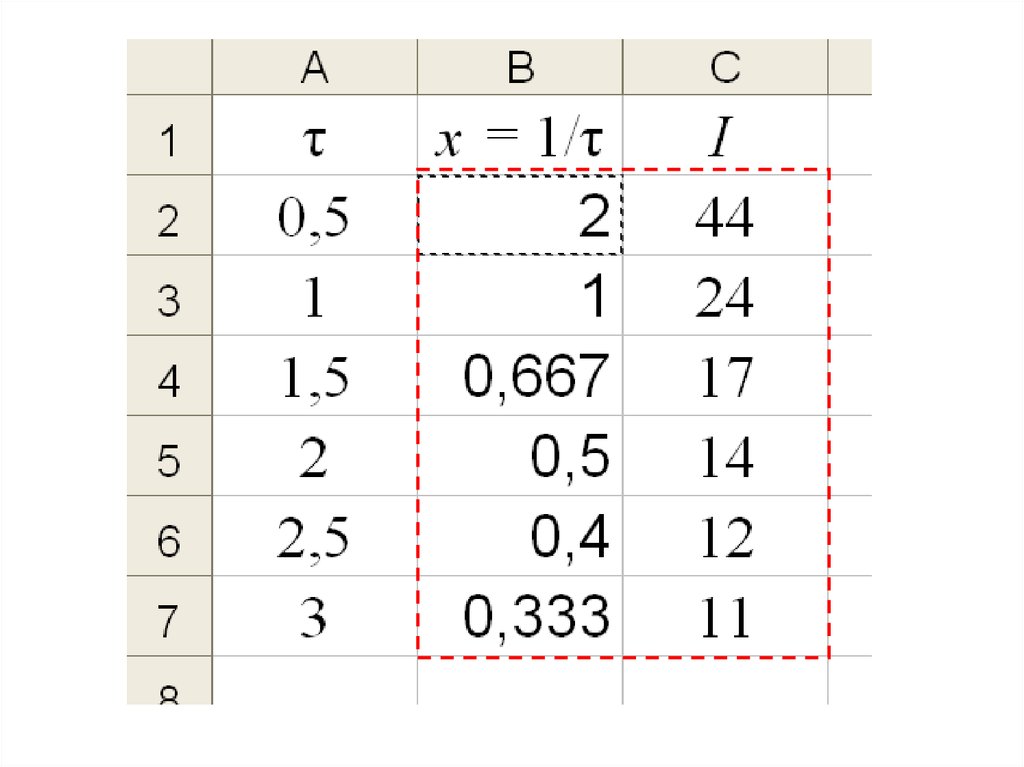
τи, мсIП, мА
0,5
44
1,0
24
1,5
17
2,0
14
2,5
12
3,0
11
9.
10.
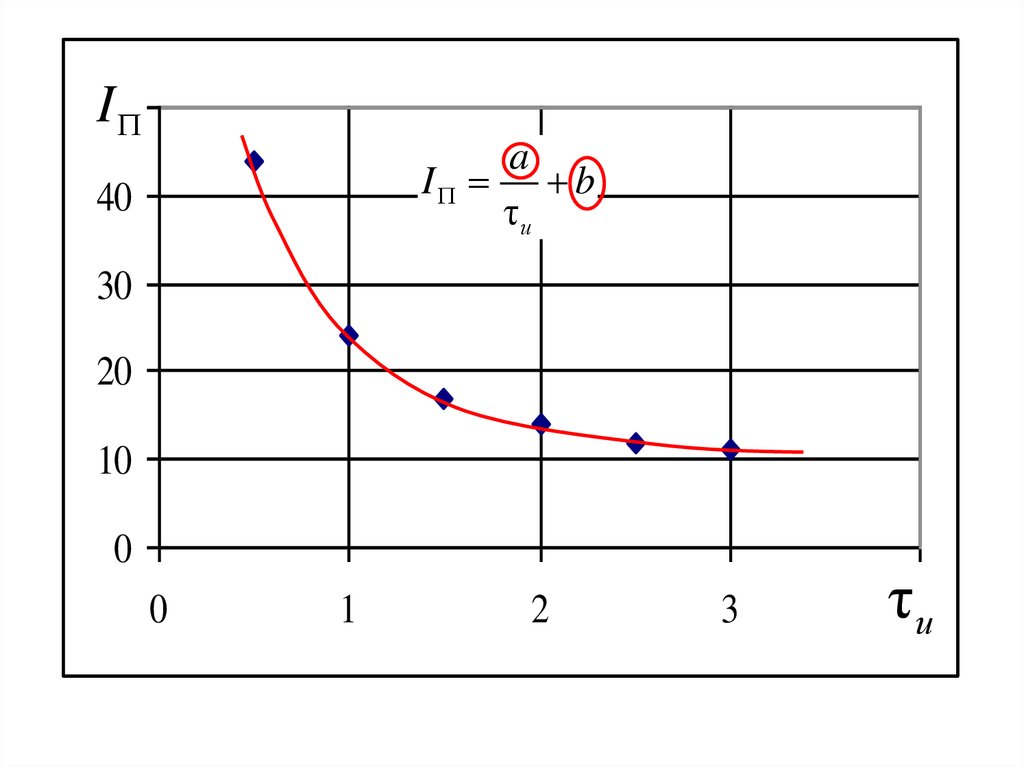
I50
a
I b
τи
40
30
20
10
0
0
1
2
3
τ4и
11.
12.
aI b – гипербола
τи
1
x
τи
I a x b
– прямая
13.
14.
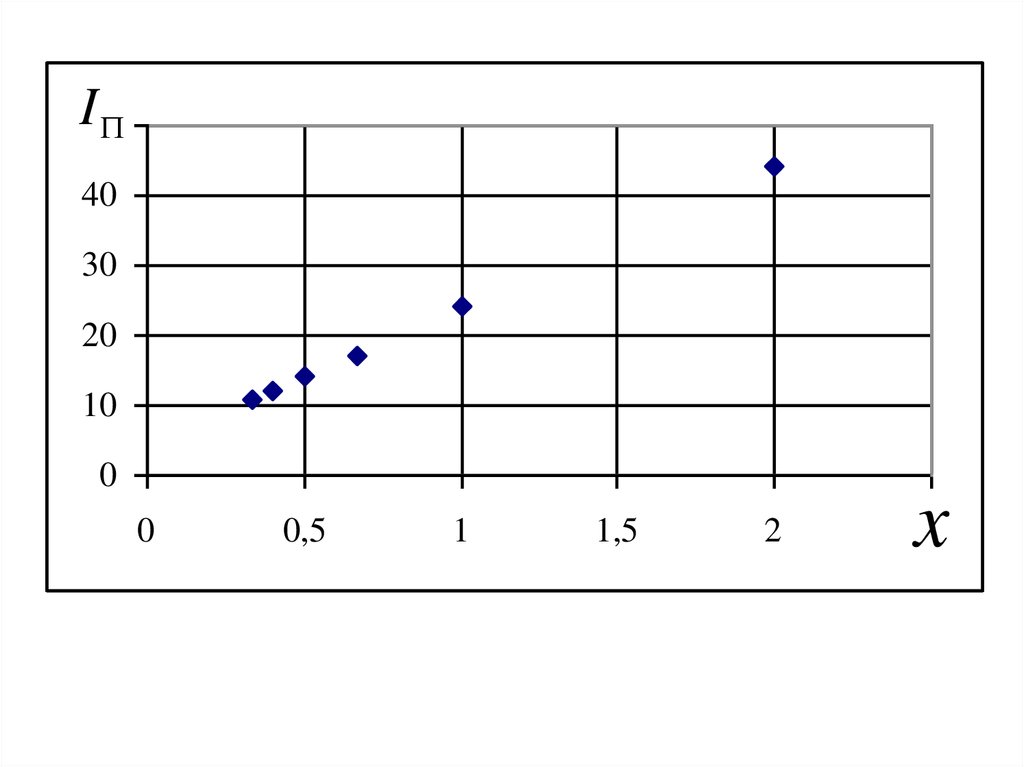
I5040
30
20
10
0
0
0,5
1
1,5
2
x
2,5
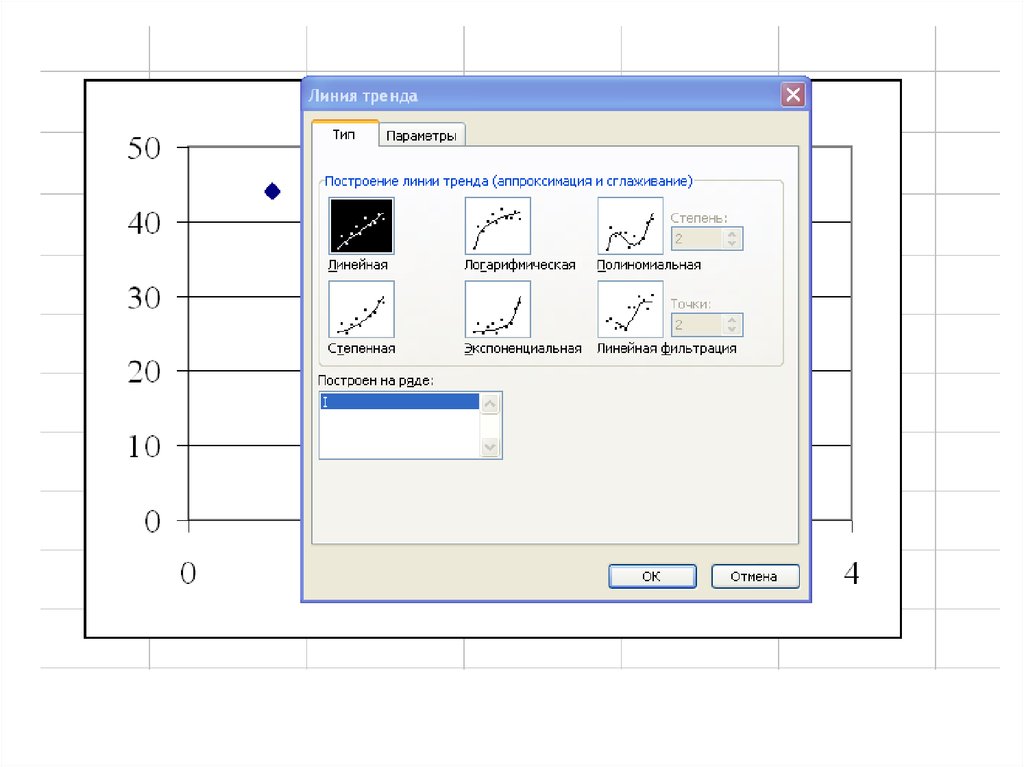
15.
16.
17.
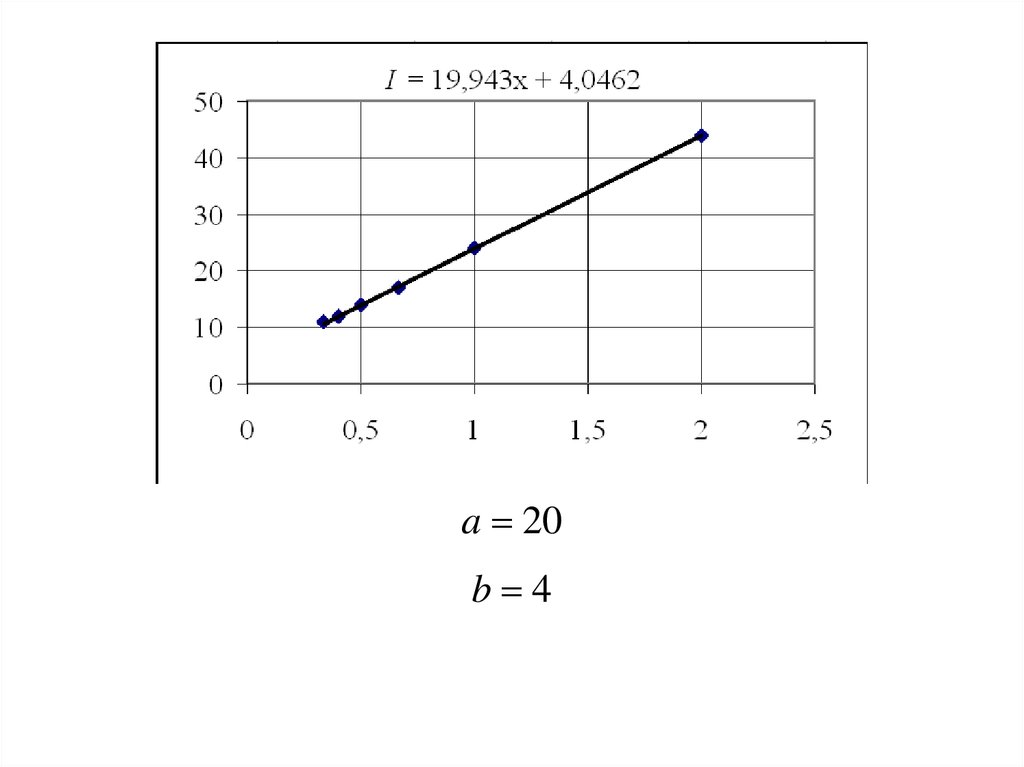
a 20b 4
18.
20I
4, мА
τи
I const R b 4
2R 8
chr = τи при IП = 2R
20
2R 8
4
chr
chr 5 мс
мА


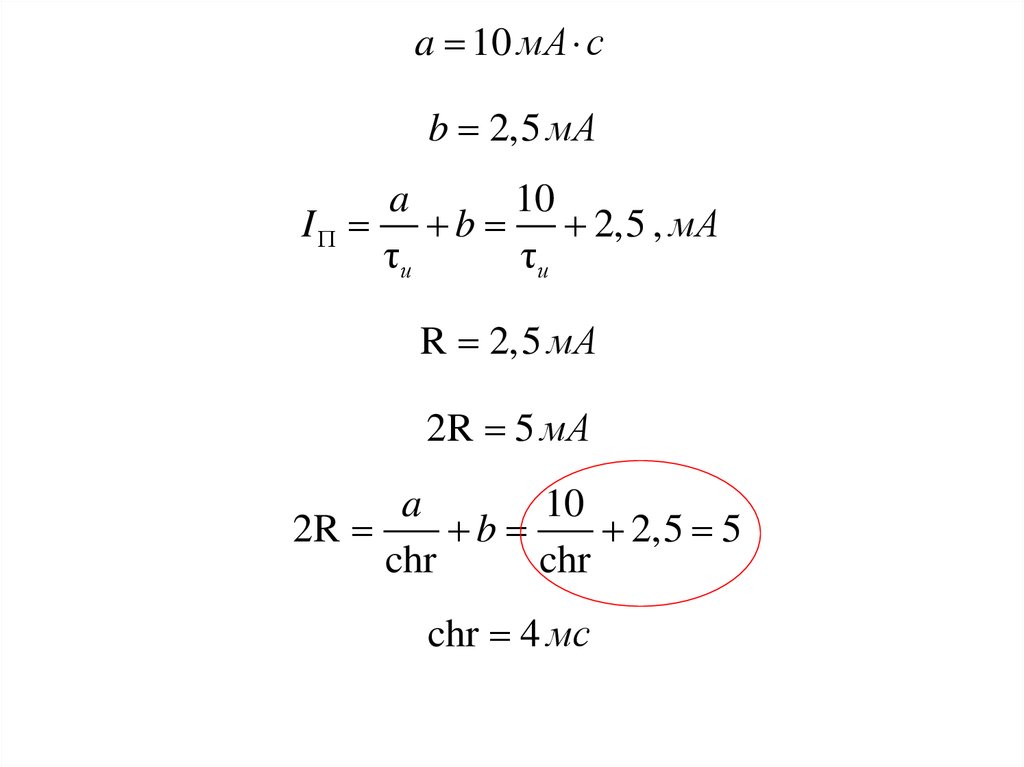



 Биология
Биология








