Похожие презентации:
Химия. Контрольная работа №3. Вариант №3. Задание №1
1.
КР 3Вариант №3
Задание №1
2.
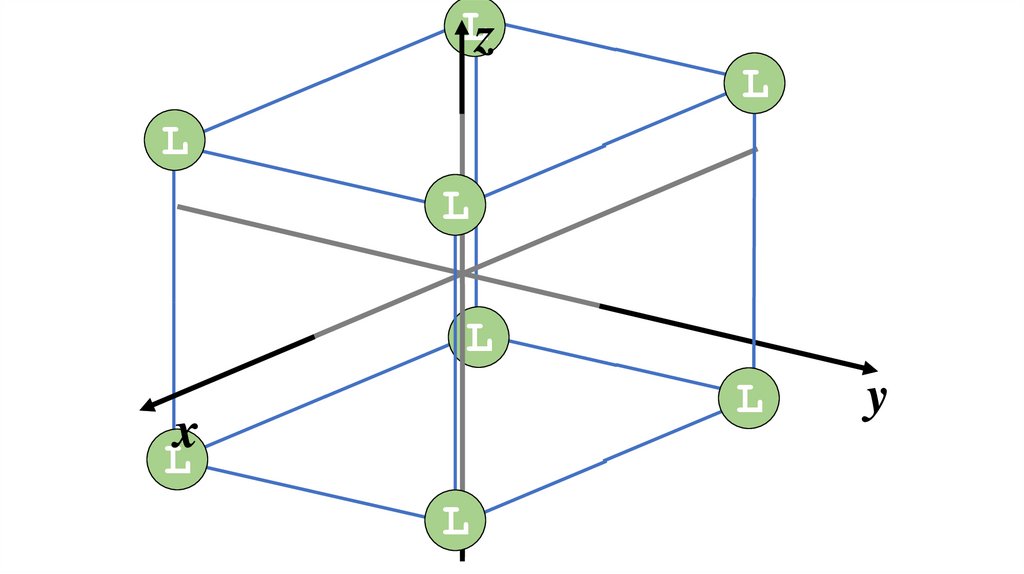
Предложите схемуперекрывания d-орбиталей в
кубическом комплексе ML8
3.
zx
y
4.
zx
y
5.
LzL
L
L
L
L
x
L
L
y
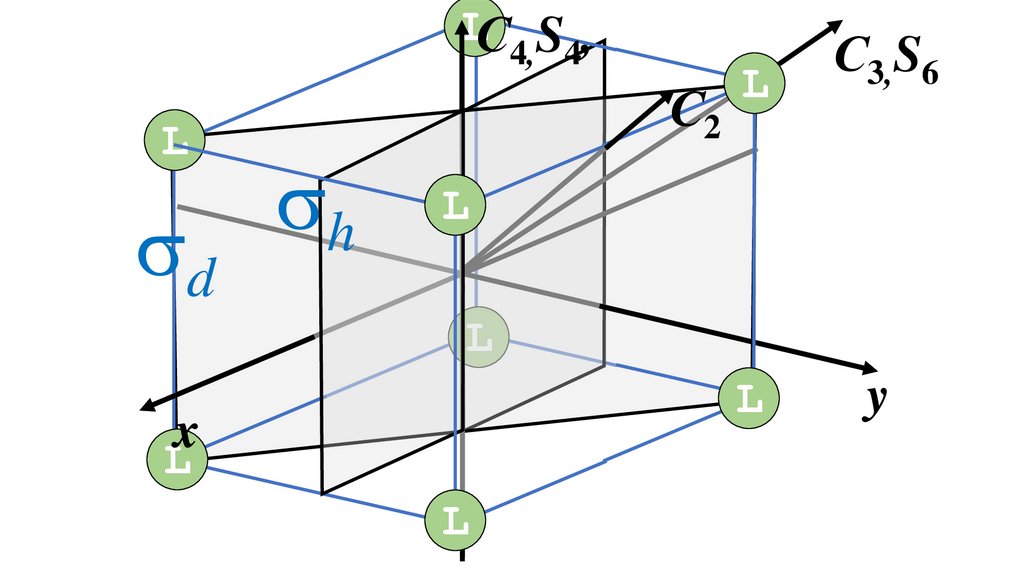
6.
LС S ,4, 4
L
sd
sh
С2
L
С3,S6
L
y
L
L
x
L
L
7.
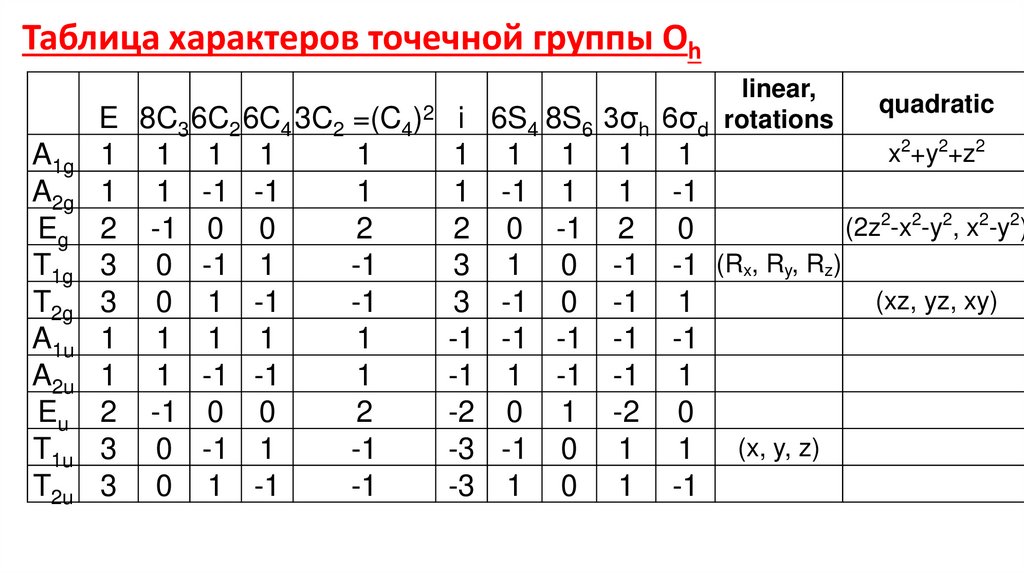
Таблица характеров точечной группы ОhA1g
A2g
Eg
T1g
T2g
A1u
A2u
Eu
T1u
T2u
E
1
1
2
3
3
1
1
2
3
3
8C3 6C2 6C4 3C2 =(C4)2
1
1
-1
0
0
1
1
-1
0
0
1
-1
0
-1
1
1
-1
0
-1
1
1
-1
0
1
-1
1
-1
0
1
-1
1
1
2
-1
-1
1
1
2
-1
-1
i
1
1
2
3
3
-1
-1
-2
-3
-3
linear,
6S4 8S6 3σh 6σd rotations
1 1
-1 1
0 -1
1 0
-1 0
-1 -1
1 -1
0 1
-1 0
1 0
1
1
2
-1
-1
-1
-1
-2
1
1
quadratic
x2+y2+z2
1
-1
(2z2-x2-y2, x2-y2)
0
-1 (Rx, Ry, Rz)
(xz, yz, xy)
1
-1
1
0
1 (x, y, z)
-1
8.
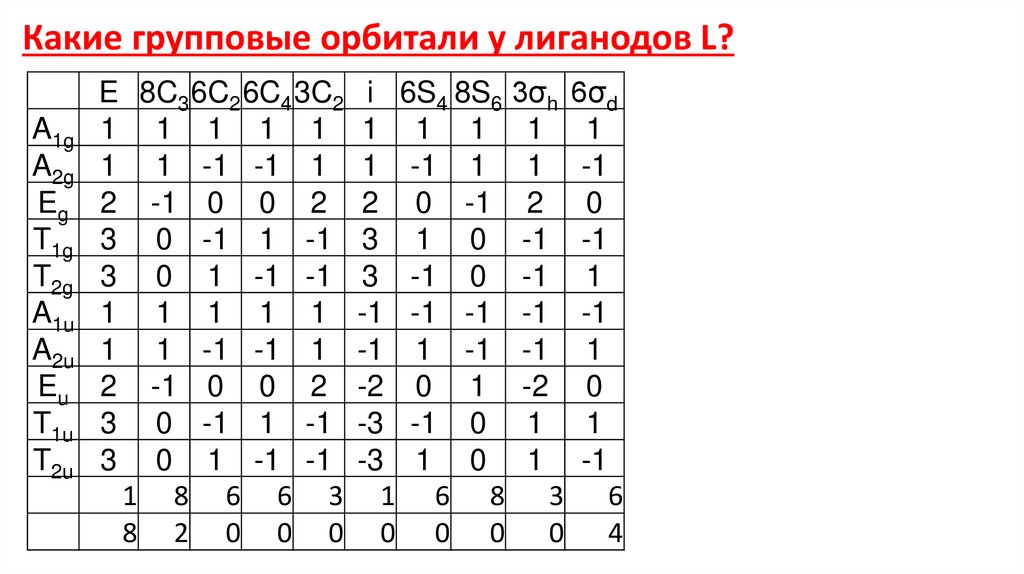
Какие групповые орбитали у лиганодов L?A1g
A2g
Eg
T1g
T2g
A1u
A2u
Eu
T1u
T2u
E 8C3 6C2 6C4 3C2 i 6S4 8S6 3σh 6σd
1 1 1 1 1 1 1 1 1 1
1 1 -1 -1 1 1 -1 1 1 -1
2 -1 0 0 2 2 0 -1 2 0
3 0 -1 1 -1 3 1 0 -1 -1
3 0 1 -1 -1 3 -1 0 -1 1
1 1 1 1 1 -1 -1 -1 -1 -1
1 1 -1 -1 1 -1 1 -1 -1 1
2 -1 0 0 2 -2 0 1 -2 0
3 0 -1 1 -1 -3 -1 0 1 1
3 0 1 -1 -1 -3 1 0 1 -1
1 8 6 6 3 1 6 8 3 6
8 2 0 0 0 0 0 0 0 4
9.
E8C3 6C2
6C4 3C2
i
6S4
8S6
3σh
6σd
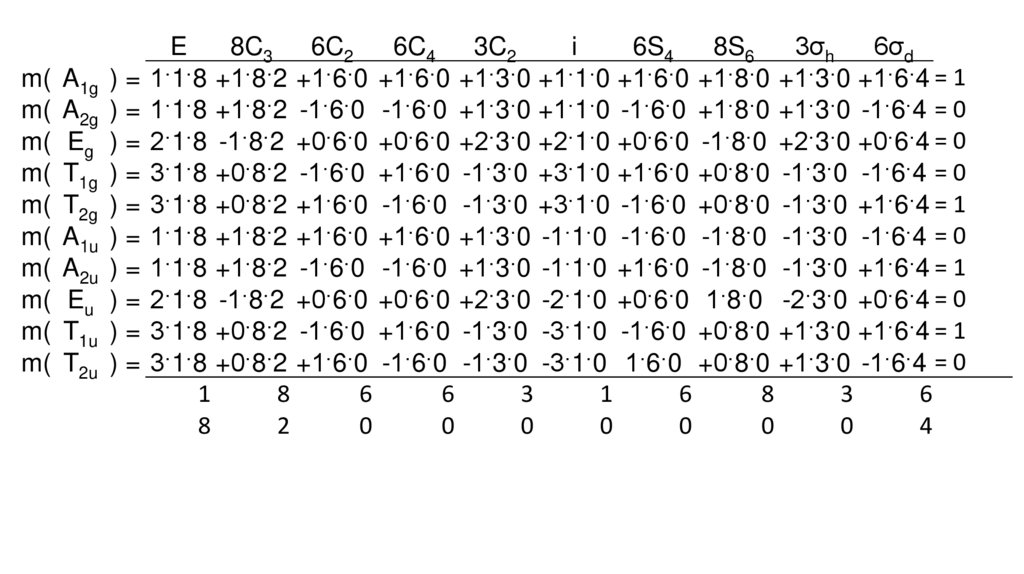
m( A1g ) = 1·1·8 +1·8·2 +1·6·0 +1·6·0 +1·3·0 +1·1·0 +1·6·0 +1·8·0 +1·3·0 +1·6·4 = 1
m( A2g ) = 1·1·8 +1·8·2 -1·6·0 -1·6·0 +1·3·0 +1·1·0 -1·6·0 +1·8·0 +1·3·0 -1·6·4 = 0
m( Eg ) = 2·1·8 -1·8·2 +0·6·0 +0·6·0 +2·3·0 +2·1·0 +0·6·0 -1·8·0 +2·3·0 +0·6·4 = 0
m( T1g ) = 3·1·8 +0·8·2 -1·6·0 +1·6·0 -1·3·0 +3·1·0 +1·6·0 +0·8·0 -1·3·0 -1·6·4 = 0
m( T2g ) = 3·1·8 +0·8·2 +1·6·0 -1·6·0 -1·3·0 +3·1·0 -1·6·0 +0·8·0 -1·3·0 +1·6·4 = 1
m( A1u ) = 1·1·8 +1·8·2 +1·6·0 +1·6·0 +1·3·0 -1·1·0 -1·6·0 -1·8·0 -1·3·0 -1·6·4 = 0
m( A2u ) = 1·1·8 +1·8·2 -1·6·0 -1·6·0 +1·3·0 -1·1·0 +1·6·0 -1·8·0 -1·3·0 +1·6·4 = 1
m( Eu ) = 2·1·8 -1·8·2 +0·6·0 +0·6·0 +2·3·0 -2·1·0 +0·6·0 1·8·0 -2·3·0 +0·6·4 = 0
m( T1u ) = 3·1·8 +0·8·2 -1·6·0 +1·6·0 -1·3·0 -3·1·0 -1·6·0 +0·8·0 +1·3·0 +1·6·4 = 1
m( T2u ) = 3·1·8 +0·8·2 +1·6·0 -1·6·0 -1·3·0 -3·1·0 1·6·0 +0·8·0 +1·3·0 -1·6·4 = 0
1
8
6
6
3
1
6
8
3
6
8
2
0
0
0
0
0
0
0
4
10.
Г = A1g + T2g + A2u + T1u11.
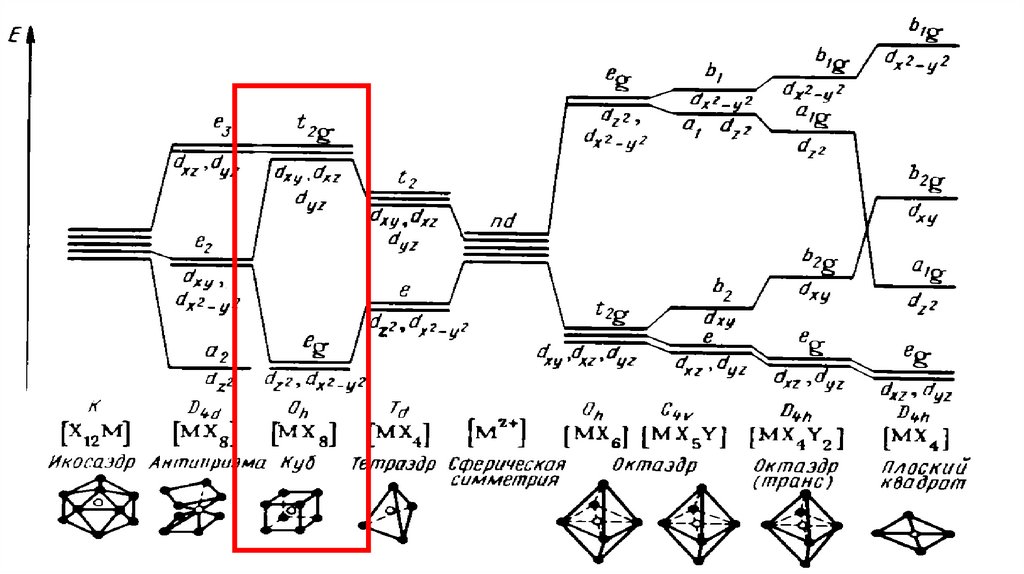
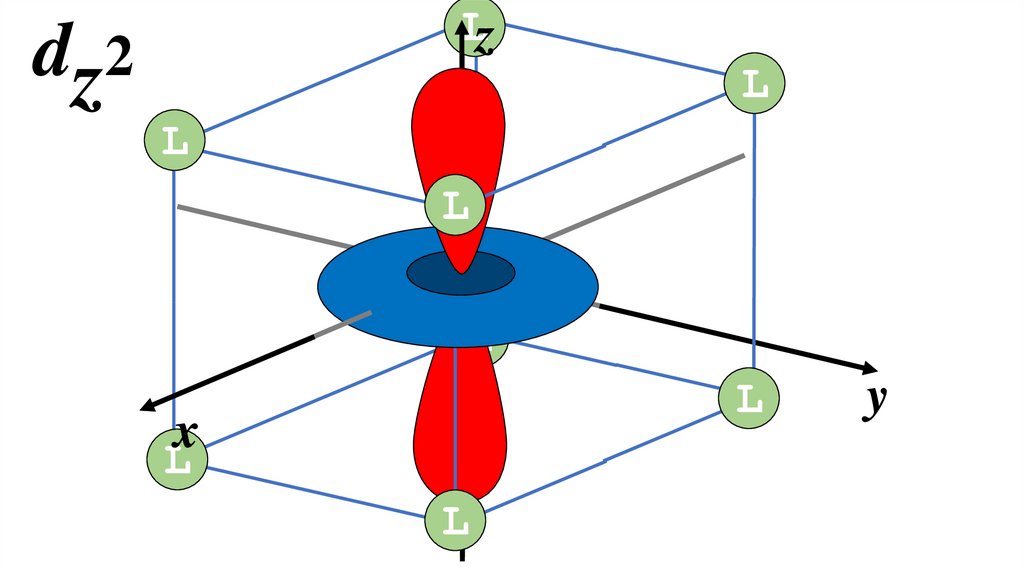
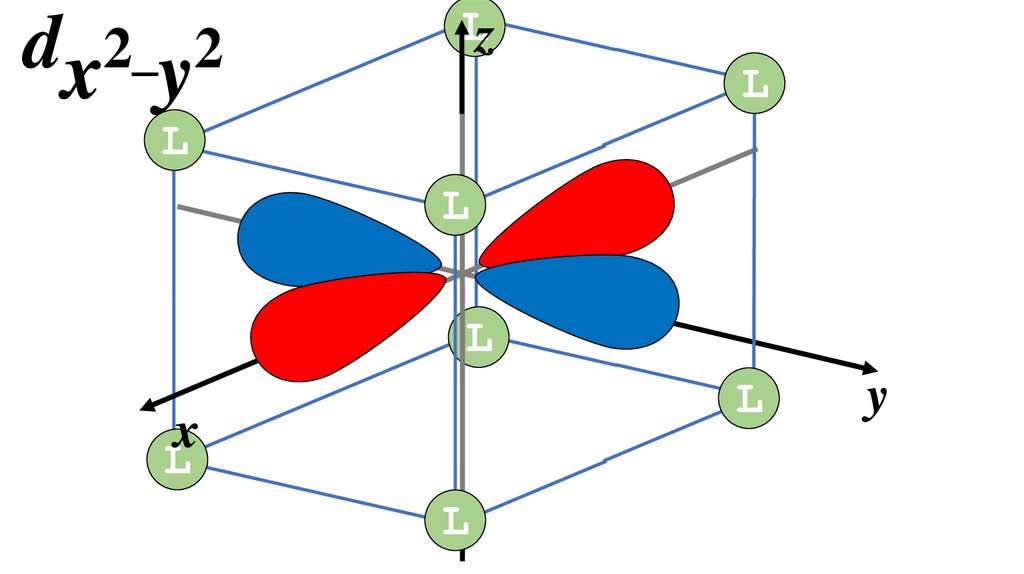
Г(d) = Eg + T2g12.
Г(d) = Eg + T2gdz2
dxy
d x 2 –y 2
dxz
dyz
13.
Г(d) = Eg + T2gГ = A1g + T2g + A2u + T1u
14.
15.
16.
dz2Lz
L
L
L
L
L
x
L
L
y
17.
dx2–y2Lz
L
L
L
L
L
x
L
L
y
18.
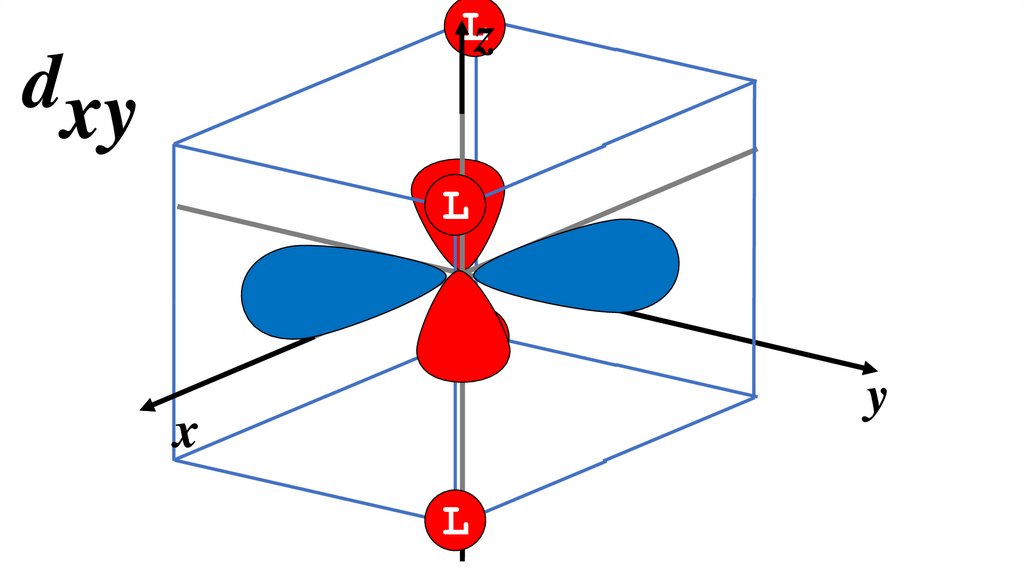
zdxy
x
y
19.
Lzdxy
L
L
y
x
L
20.
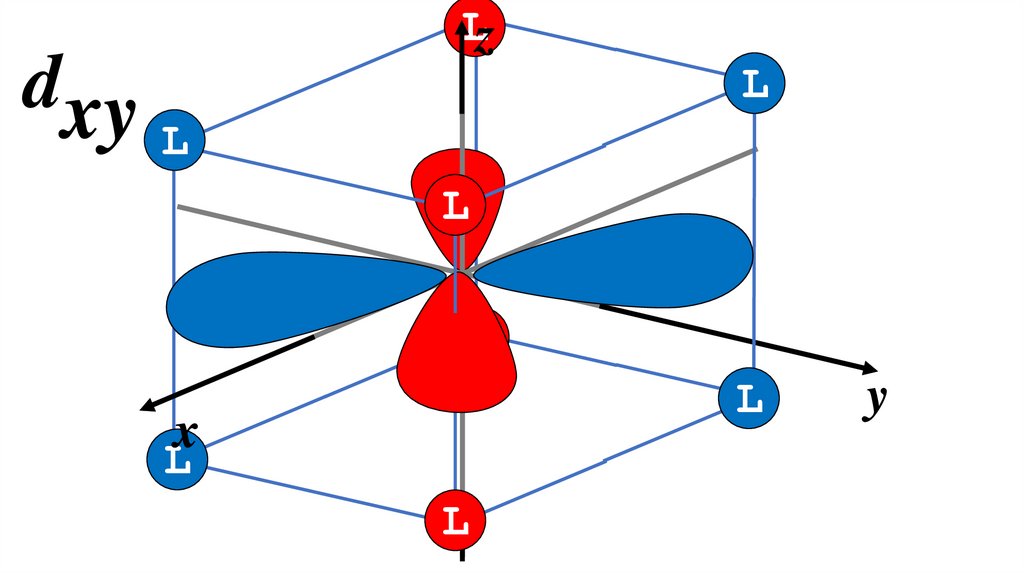
dxyLz
L
L
L
L
L
x
L
L
y
21.
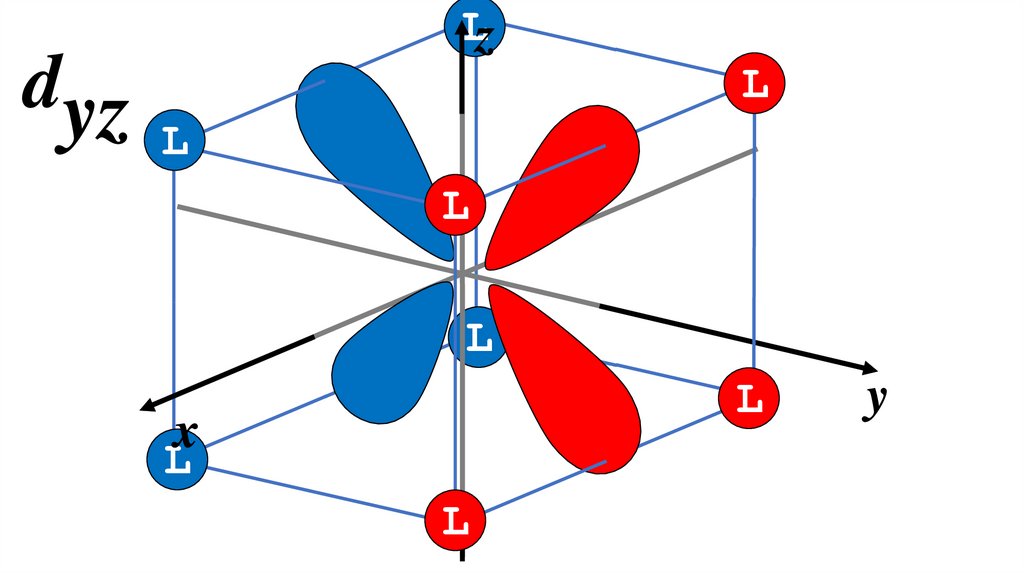
dyzLz
L
L
L
L
L
x
L
L
y
22.
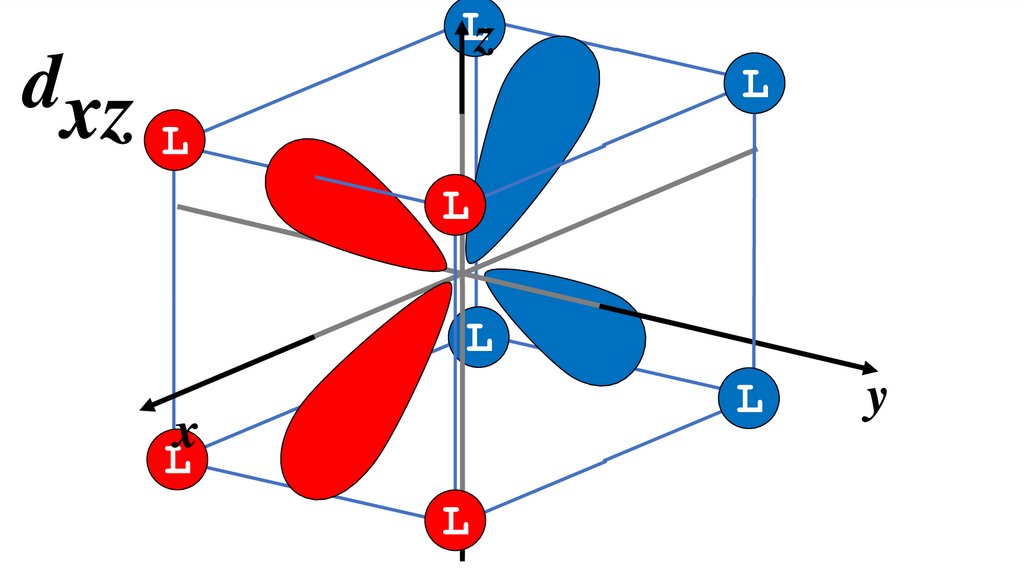
dxzLz
L
L
L
L
L
x
L
L
y
23.
КР 3Вариант №3
Задание №1
24.
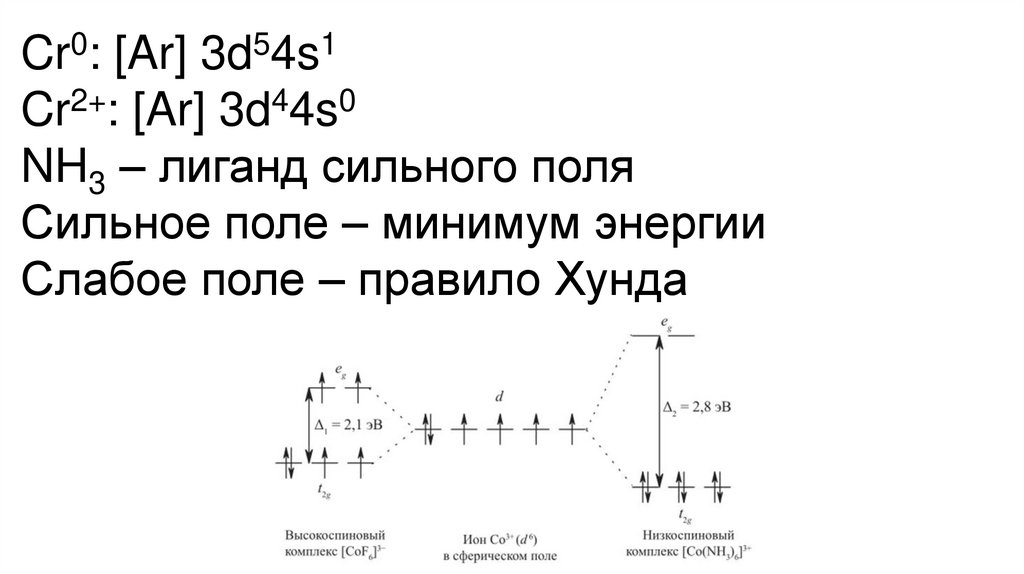
Сколько полос поглощения следуетожидать в электронном спектре
комплекса [Cr(NH3)6]2+, будет ли для него
проявляться эффект Яна-Теллера?
25.
Cr0: [Ar] 3d54s1Cr2+: [Ar] 3d44s0
NH3 – лиганд сильного поля
Сильное поле – минимум энергии
Слабое поле – правило Хунда
26.
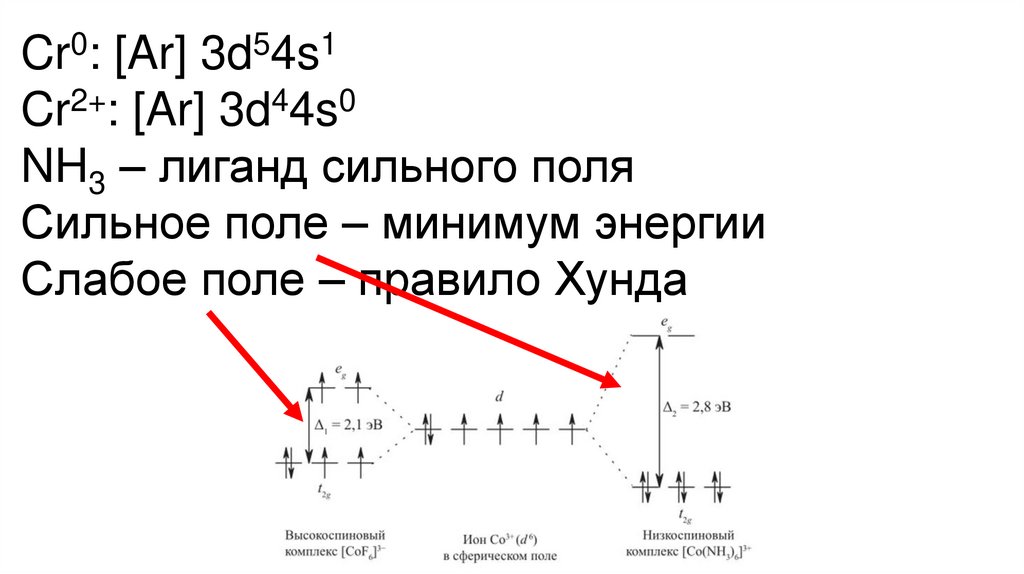
Cr0: [Ar] 3d54s1Cr2+: [Ar] 3d44s0
NH3 – лиганд сильного поля
Сильное поле – минимум энергии
Слабое поле – правило Хунда
27.
Cr0: [Ar] 3d54s1Cr2+: [Ar] 3d44s0
NH3 – лиганд сильного поля
Сильное поле – минимум энергии
Слабое поле – правило Хунда
28.
Cr0: [Ar] 3d54s1Cr2+: [Ar] 3d44s0
NH3 – лиганд сильного поля
Сильное поле – минимум энергии
Слабое поле – правило Хунда
29.
Cr0: [Ar] 3d54s1Cr2+: [Ar] 3d44s0
NH3 – лиганд сильного поля
Сильное поле – минимум энергии
Слабое поле – правило Хунда
30.
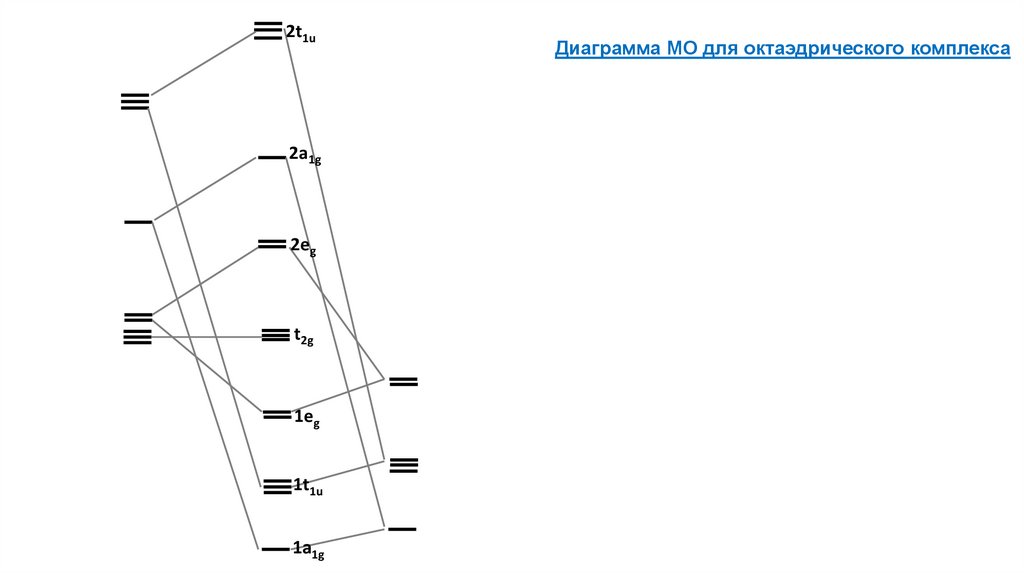
2t1u2a1g
2eg
t2g
1eg
1t1u
1a1g
Диаграмма МО для октаэдрического комплекса
31.
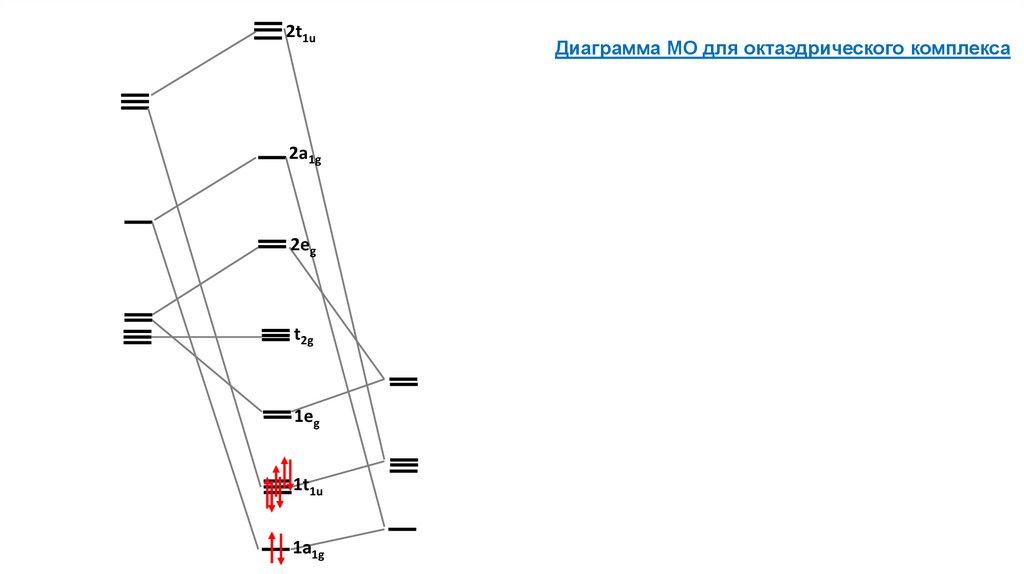
2t1u2a1g
2eg
t2g
1eg
1t1u
1a1g
Диаграмма МО для октаэдрического комплекса


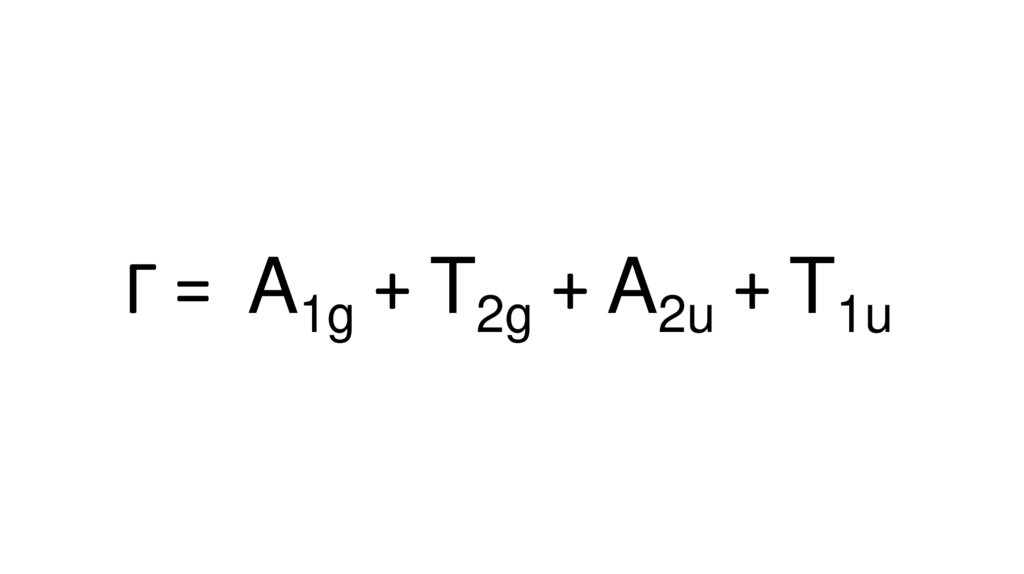
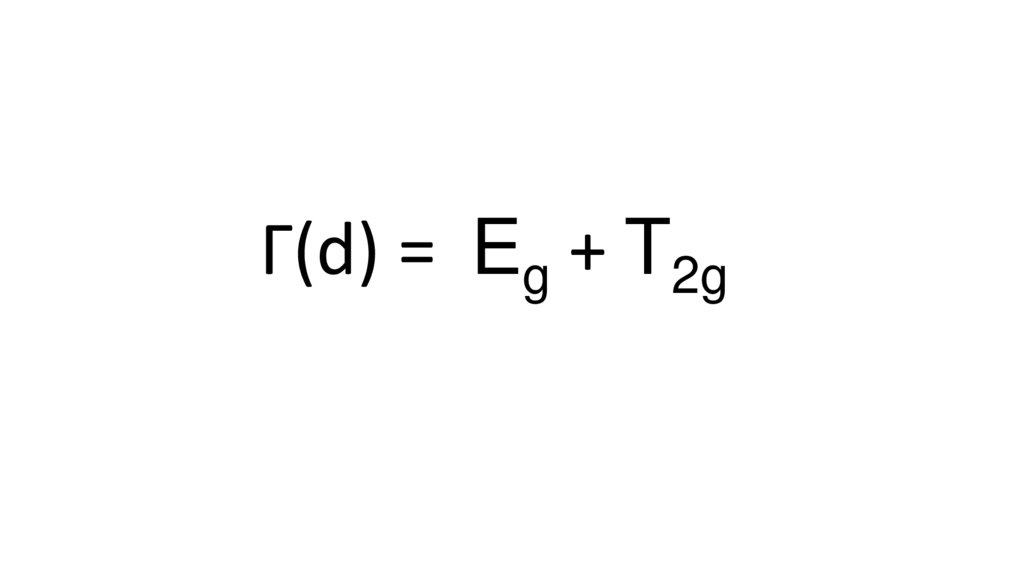
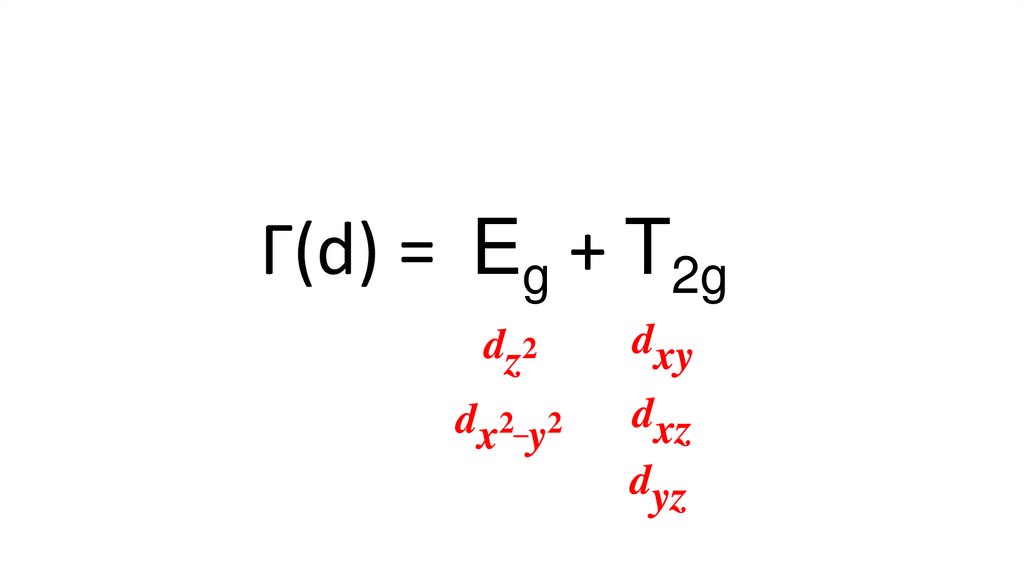
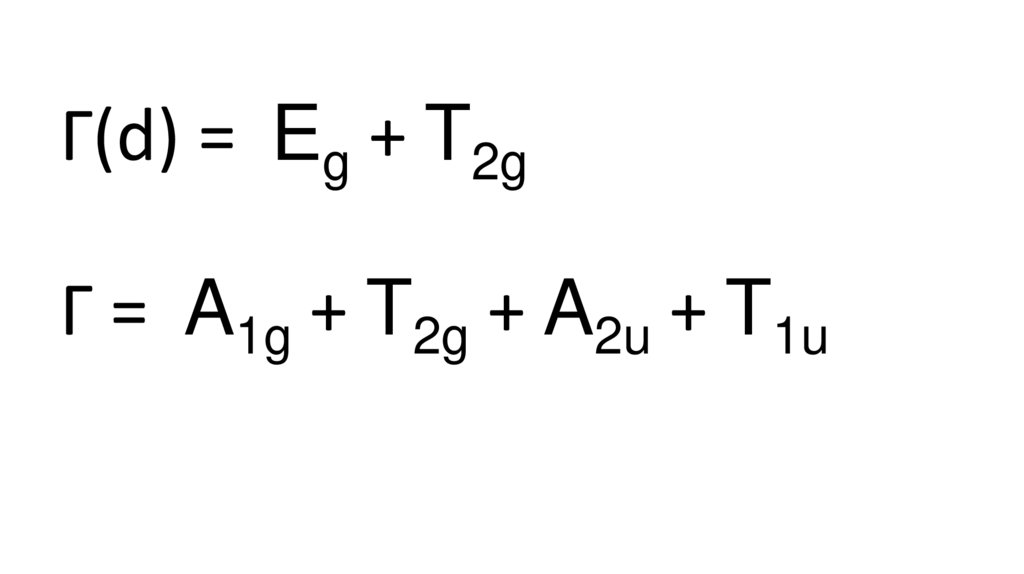





 Химия
Химия








