Похожие презентации:
Прикладные задачи нелинейной динамики. Условия возникновения диссипативных структур. Неустойчивость Тьюринга
1.
Центр дистанционного обученияПрикладные задачи
нелинейной динамики
ФИО преподавателя: Е.Н.Пронина
e-mail: pvi173@rambler.ru
Online-edu.mirea.ru
mirea.ru
2.
Центр дистанционного обученияЛекция № 15.
Условия возникновения диссипативных
структур. Неустойчивость Тьюринга.
mirea.ru
3.
Список литературы:Центр дистанционного обучения
• Ризниченко Г.Ю. Математические модели в биологии. Учебное
пособие биологического факультета МГУ:
http://mathbio.ru/lectures/
• Неустойчивость Тьюринга, сайт Калтехаhttp://www.cmp.caltech.edu/~mcc/BNU/Notes7_2.pdf
• Распределенная модель брюсселятора. – Электронный ресурс:
Режим доступа:
https://mathit.petrsu.ru/users/semenova/Nonlinear_Dynamics/ND_20
17_PMI.html от 05.05.2019
• J.L.Guiňon and E.Ortega. Simulation of the Turing Patterns in the
Brusselator model with MathCAD.// Univeridad Politecanica De
Valencia. // https://www.youtube.com/wanch
mirea.ru
4.
Центр дистанционного обученияА.М.Тьюринг "Химические основы морфогенеза " (1952)
Если химическая реакция с диффузией протекает в однородной
среде и продукты реакции остаются в том же объёме, то они
постепенно распределяются в нём равномерно, и это
распределение является стабильным.
Когда же продукты реакции могут уходить (диффундировать) в
окружающее пространство, то в случае недостаточной для
эффективного
перемешивания
скорости
первоначально
однородная среда становится неравновесной, и в ней может
установиться периодическое в пространстве и стационарное
во времени распределение концентраций - чередующиеся
сгущения и разрежения продуктов реакции.
mirea.ru
5.
Центр дистанционного обученияЧередования сгущений и разрежений называют «узоры
Тьюринга», а механизм их образования «pattern formation».
Неустойчивость однородного состояния
тьюринговой неустойчивости.
носит
название
Структура Тьюринга − стационарная двумерная структура
нелинейной динамики, возникающая вследствие волновых
свойств реакционно-диффузионных систем.
Три базовых вида структур Тьюринга: гексагональные пятна,
полосы, структуры типа пчелиных сот.
mirea.ru
6.
Центр дистанционного обученияСистема уравнений в частных производных
реакция-диффузия
x
2 x
t P( x, y, r ) Dx r 2
(1)
2
y
Q ( x, y , r ) D y
y
t
r 2
Модель химической реакции в
распределенной системе:
два вещества c концентрациями x и y.
r - пространственная переменная,
t- время,
D – коэффициенты диффузии,
P и Q –известные функции
x
x
y
y
(2)
0
r r 0 r r L r r 0 r r L
Краевые условия
непроницаемости
реактора.
–
условия
торцов
mirea.ru
7.
Центр дистанционного обученияПространственно однородное
стационарное состояние:
(гомогенное)
состояние, при котором значения переменных не
меняются со временем и одинаковы в
каждой
точке пространства.
mirea.ru
8.
x x, y yЦентр дистанционного обучения
Точечная система
Исследование
устойчивости
распределенной
и точечной
системы:
dx
P ( x, y )
dt
dy Q ( x, y ) (3)
dt
Рассмотрим
состояние системы
такое что:
dx dy
0
dt dt x , y
Распределенная система
x
2 x
P ( x , y , r ) Dx 2
t
r
2
y Q ( x, y , r ) D y
y
r 2
t
(3′)
Рассмотрим
пространственно
однородное
стационарное
стационарное
решение системы x x, y y
,
x x, y y
такое, что:
(4)
x y x y
0
t t r r x , y
(4′)
P(x,y,r) = 0, Q(x,y,r) = 0
mirea.ru
9.
Центр дистанционного обученияСтационарное состояние
Пространственно однородное
устойчиво, если малые отклонения стационарное состояние устойчиво,
не выводят систему слишком далеко если малые отклонения (в том числе и
из окрестности этого состояния.
распределенные в пространстве) не
выводят систему слишком далеко из
окрестности
этого состояния.
Пусть ξ(t) и η(t) – малые отклонения
от стационарных решений
Пусть ξ(t,r) и η(t,r) – малые
отклонения от пространственно
однородных стационарных решений
mirea.ru
10.
Центр дистанционного обученияДля ξ и η можно записать
линеаризованную систему:
d
a b
dt
d c d
dt
(5)
Для ξ и η можно записать
распределенную линеаризованную
систему:
2
t a b D r 2
2
(5′)
d c d D
dt
r 2
Dξ =Dx ,
a
Dη =Dy
P( x, y )
P( x, y )
Q( x, y )
Q( x, y )
,b
,c
,d
x
y
x
y
(6)
mirea.ru
11.
Центр дистанционного обученияРешение будем искать в виде:
Решение будем искать в виде:
ξ(t)=Aeλt
η(t)=Beλt
ξ(t, r)=Aept+ikr
η(t,r)=Bept+ikr
(7′)
ept характеризует поведение
Множитель
отклонения от стационарного состояния во
времени.
Множитель eikr - отклонение переменных
от однородного
стационарного
λt
Множитель e
характеризует состояния
в
точке
с
поведение отклонения от
координатой r для собственных функций,
соответствующих
волновому
числу
k.
стационарного состояния во времени.
Для
трубки
длиной
l
волновое число принимает дискретные
значения: k k 2 n
.
n
l
mirea.ru
(7)
12.
Центр дистанционного обученияПодстановка выражений (7) в (5)
после сокращения на eλt дает
A aA bB,
B cA dB,
или
( a ) A bB 0,
cA ( d ) B 0.
(8)
(9)
Подстановка выражений (7′) в (5′)
после сокращения на ept· eikr дает
2
pA
aA
bB
k
D A,
2
pB
cA
dB
k
D B,
или
2
(
p
a
k
D ) A bB 0,
2
cA
(
p
d
k
D )B 0.
(8 )
(9 )
mirea.ru
13.
Центр дистанционного обучения( a ) A bB 0,
cA ( d )B 0.
2
( p a k D ) A bB 0,
2
cA ( p d k D ) B 0.
(9)
(9 )
Величины A, B тождественно не равны нулю тогда и только тогда, когда
определитель систем (9) и (9′) равен нулю:
( a)( d ) bc 0,
Характеристическое уравнение:
2 0, где
a d,
ad bc.
( p a k 2 D )( p d k 2 D ) bс 0
Дисперсионное уравнение:
p 2 1 p 1 0, где
1 a d k 2 ( D D ),
1 k 4 D D k 2 (aD dD ) ad bc.
mirea.ru
14.
ss2
l 1,2 = ±
- D
2
4
Бифуркационная диаграмма 1
Центр
дистанционного
обучения
1 2
1
(s ) 1
s
p1,2 =
±
- D
2
4
Бифуркационная диаграмма 2
mirea.ru
15.
Центр дистанционного обученияНЕУСТОЙЧИВОСТЬ ТЬЮРИНГА
Условия возникновения диффузионной
неустойчивости
(обусловленной только процессами диффузии):
mirea.ru
16.
Центр дистанционного обученияОднородное стационарное состояние x x, y y ,
будет устойчивым по отношению к малым однородным
возмущениям (когда нет возмущения по пространству и точечная
система устойчива)
и не устойчиво по отношению к малым пространственно
неоднородным возмущениям, когда:
1) σ < 0, ∆>0 (условие устойчивости в точечной
системе),
2) σ1 > 0, (1-е условие неустойчивости в распределенной
системе), либо
3)∆1 < 0 (2-е условие неустойчивости в распределенной
системе).
mirea.ru
17.
Центр дистанционного обученияПри
положительных
диффузии (Dx>0, Dy>0) и σ<0
коэффициентах
выражение
σ1 =a + d − k2(Dx+ Dy)< 0,
т.к. σ = a+d < 0, то есть первое условие неустойчивости в
распределенной системе не выполняется.
Следовательно, для возникновения неустойчивости в
распределенной системе необходимо выполнение второго
неравенства: ∆1 < 0 (седловая неустойчивость).
mirea.ru
18.
Центр дистанционного обученияДля возникновения диффузионной
неустойчивости (неустойчивости Тьюринга)
необходимо одновременное выполнение следующих
условий:
1) a d 0,
2) ad bc 0,
( 0)
( 0)
3) =k Dx D y k ( aDy dDx ) ad bc 0
1
4
2
mirea.ru
19.
Центр дистанционного обученияПонятие активатора и ингибитора
k Dx Dy k ( aDy dDx ) ad bc 0
1
4
2
0
0
k 2 ( aD y dDx ) 0 ( aD y dDx ) 0
aD y dDx 0
а положительный,
a d 0
d – отрицательный или наоборот
mirea.ru
20.
Центр дистанционного обученияПусть a >0, а d <0.
Вещество x − активатор (a·x автокаталитический член),
вещество y – ингибитор.
Коэффициент
a должен быть по модулю меньше,
чем
коэффициент d,
|a|<|d|
иначе условие
1) a+d<0
не будет выполняться
mirea.ru
21.
Центр дистанционного обучения( aD y dDx ) 0 Dx ( a
Dy
Dx
d) 0
Если a 0, d 0, и a d 0, то
Dy
Dy
(a
d ) 0, только когда
1
Dx
Dx
или D y Dx
mirea.ru
22.
Центр дистанционного обученияНеобходимым (но не достаточным) условием
возникновения диффузионной неустойчивости
является выполнение следующих требований:
1) коэффициенты a и d должны быть разных знаков;
2) коэффициент диффузии активатора меньше коэффициента
диффузии ингибитора; Dy Dx
при равных коэффициентах диффузии
диффузионная неустойчивость возникнуть не
может!
mirea.ru
23.
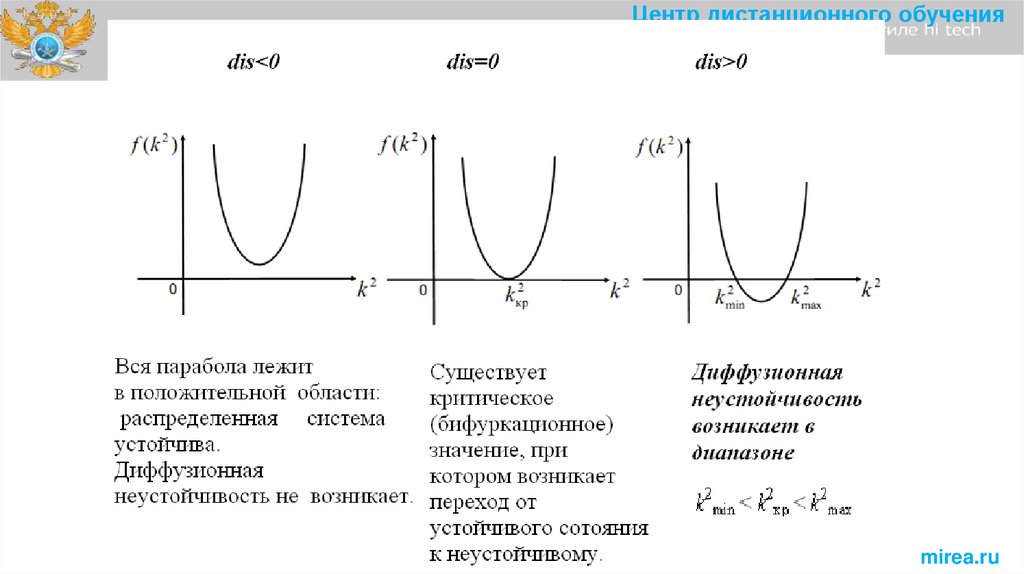
Центр дистанционного обученияСООТНОШЕНИЕ КОЭФФИЦИЕНТОВ ДИФФУЗИИ
ПРИ ВОЗНИКНОВЕНИИ ДИССИПАТИВНЫХ
СТРУКТУР:
f (k 2 ) k 4 Dx Dy k 2 (aDy dDx ) 0
dis aDy dDx 4Dx D y , где ad bc
2
mirea.ru
24.
Центр дистанционного обученияmirea.ru
25.
Центр дистанционногообучения
Критическое соотношение коэффициентов
D:
aD dD 4D D 0
2
dis 0 :
y
Обозначим : Dкр
x
Dy
Dx
x
y
, тогда
2
2
2
aD
d
4
D
0
или
a
D
2(
ad
2
)
D
d
0
кр кр
кр
кр
2
2 ad 2 ad
Dкр ,1
,
2
a
2 ad 2 ad
Dкр ,2
.
2
a
kкр2 >0 только при Dкр,1.
mirea.ru
26.
Центр дистанционного обученияДля возникновения диффузионной неустойчивости,
.
необходимо выполнение следующих
условий:
1) a+d < 0 , a >0, d <0
(либо a <0, d >0 ),
2) ad −bc > 0 ,
3) отношение коэффициента диффузии ингибитора к
коэффициенту диффузии активатора должно быть больше, чем
Dкр
2 ad 2 ad
a2
Волновое число находим из решения квадратного уравнения 1 0
k
2
кр
aDкр d
2 Dx Dкр
kкр
Число волн на отрезке единичной длины 2
mirea.ru
27.
Центр дистанционного обученияВыводы
Если один из компонентов химической реакции
(ингибитор) диффундирует значительно быстрее, чем другой
(активатор), то в нелинейной диссипативной системе
возможно возникновение неоднородных стационарных
пространственных структур.
Этот результат является далеко не тривиальным, так как
обычно считается, что диффузия выравнивает разницу
концентраций, а не производит ее: пространственно
однородное состояние, устойчивое в отсутствие диффузии,
становится неустойчивым при ее учете.
mirea.ru
28.
Центр дистанционного обученияРаспределенный брюсселятор
(система реакция-диффузия):
x
2 x
2
t A x y ( B 1) x Dx r 2
2
y
Bx x 2 y D y
y
t
r 2
Dкр
Dy
Dx
A2
B 1
2
B 1
k
2
кр
Dx
kкр 1
n
2 2
B 1
Dx
mirea.ru
29.
Центр дистанционного обученияПетрозаводский государственный университет.
Кафедра прикладной математики и кибернетики.
Дисциплина: Математические модели нелинейной динамики.
Доцент Семенова Е.Е.
Электронный ресурс:
https://
math-it.petrsu.ru/users/semenova/Nonlinear_Dynamics/ND_2017_PMI.html
mirea.ru
30.
Центр дистанционного обученияmirea.ru
31.
Центр дистанционного обученияmirea.ru
32.
Центр дистанционного обученияmirea.ru
33.
Центр дистанционного обученияmirea.ru
34.
Центр дистанционного обученияmirea.ru
35.
Центр дистанционного обученияmirea.ru
36.
Центр дистанционного обученияmirea.ru
37.
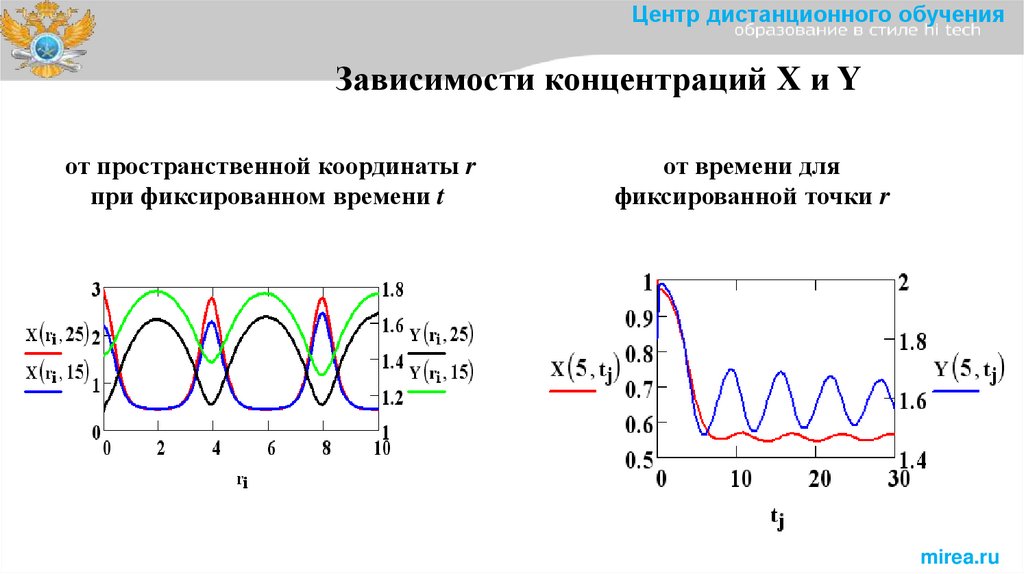
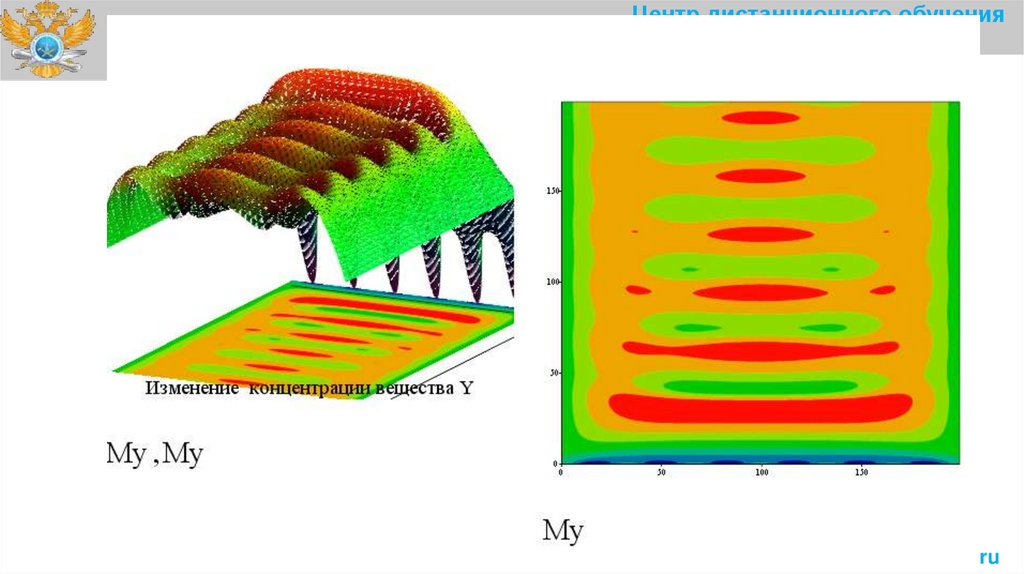
Центр дистанционного обученияЗависимости концентраций X и Y
от пространственной координаты r
при фиксированном времени t
от времени для
фиксированной точки r
mirea.ru
38.
Центр дистанционного обученияmirea.ru
39.
Центр дистанционного обученияJ.L.Guiňon and E.Ortega. Simulation of the Turing Patterns in
the Brusselator model with MathCAD// Univeridad Politecanica
De Valencia.
Электронный ресурс: https://www.youtube.com/wanch
mirea.ru
40.
Центр дистанционного обученияmirea.ru
41.
Центр дистанционного обученияmirea.ru
42.
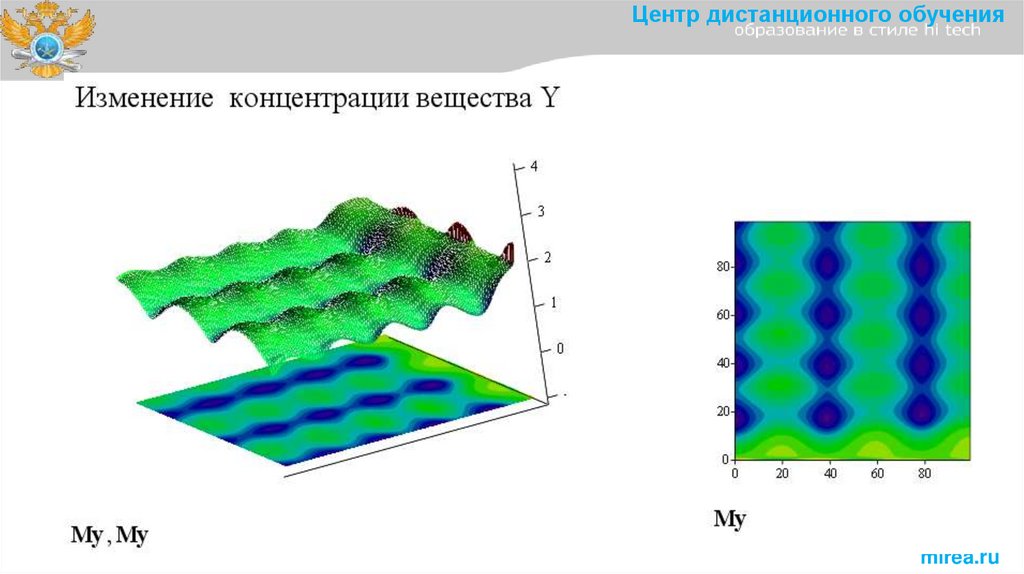
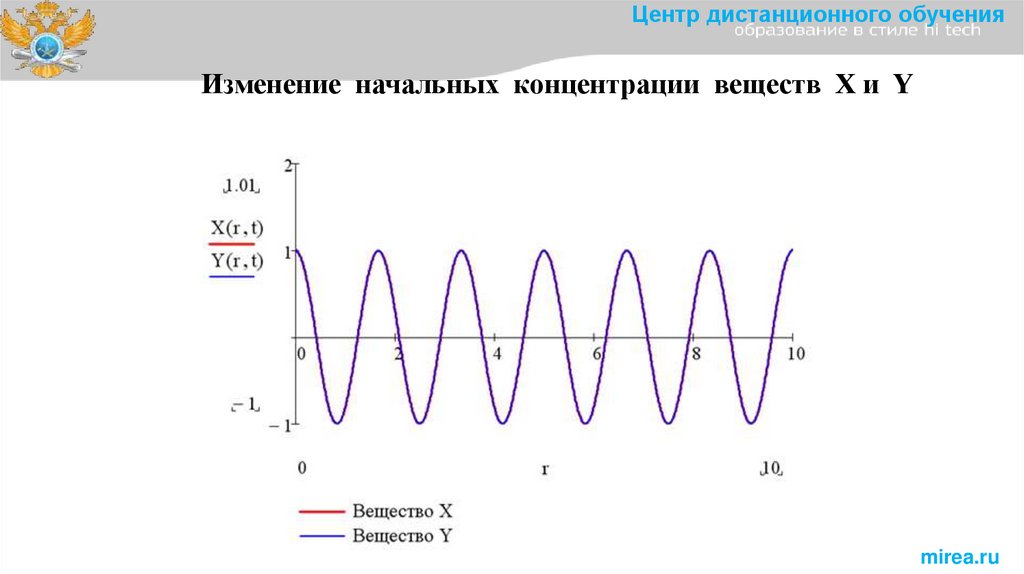
Центр дистанционного обученияИзменение начальных концентрации веществ X и Y
mirea.ru
43.
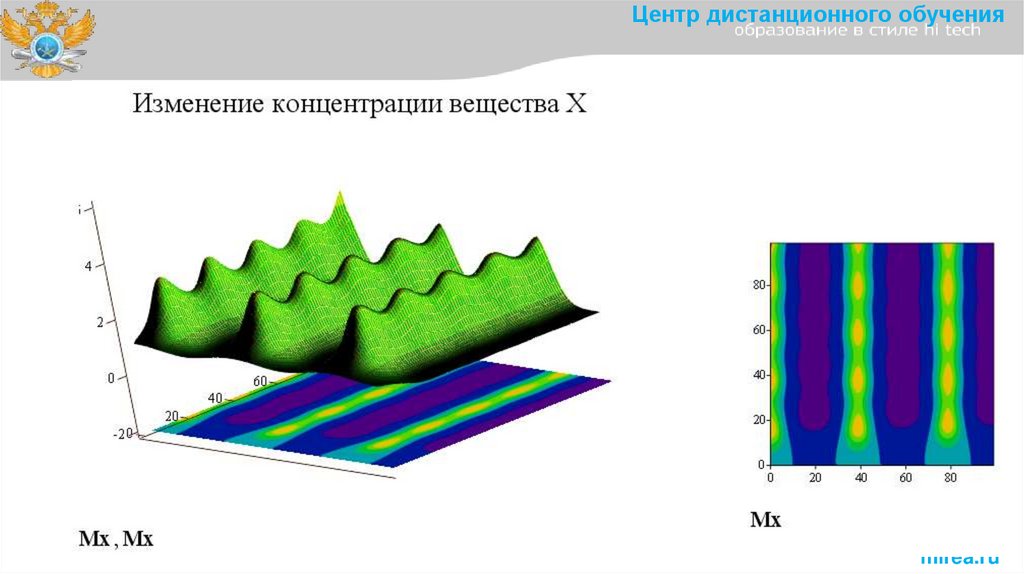
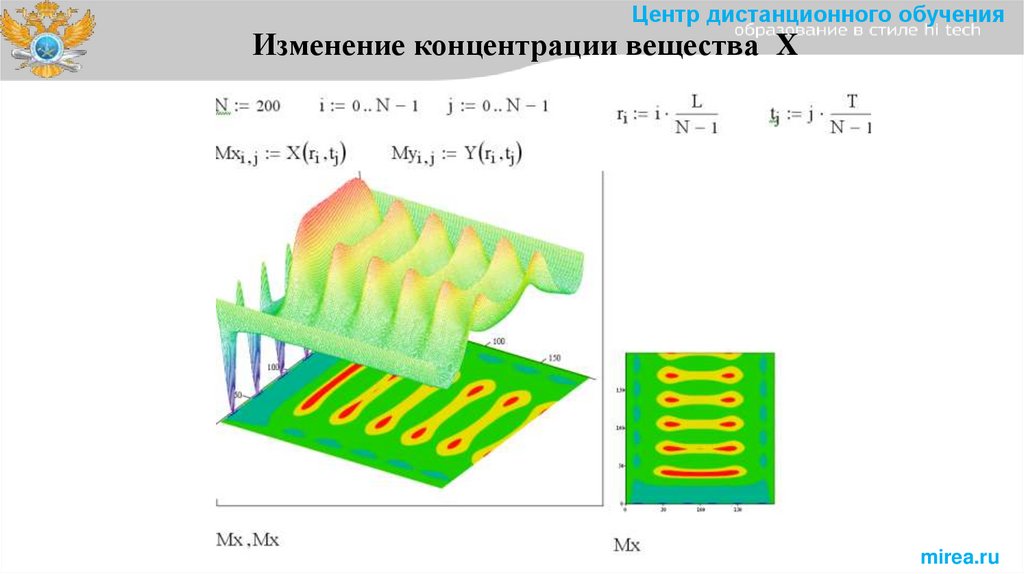
Центр дистанционного обученияИзменение концентрации вещества X
mirea.ru
44.
Центр дистанционного обученияmirea.ru
45.
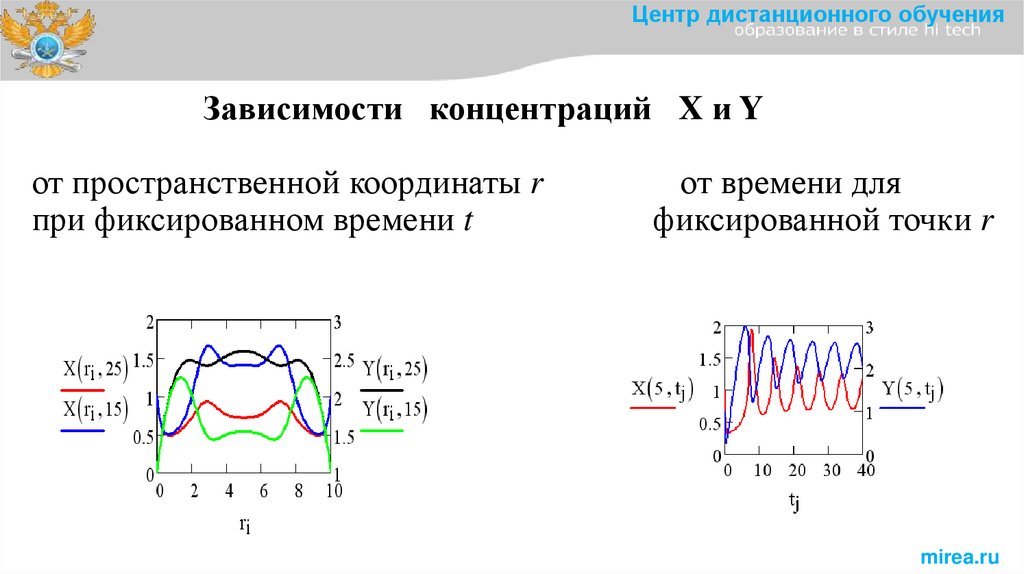
Центр дистанционного обученияЗависимости концентраций X и Y
от пространственной координаты r
при фиксированном времени t
от времени для
фиксированной точки r
mirea.ru
46.
Центр дистанционного обученияБлагодарю за внимание!
mirea.ru






































 Математика
Математика








