Похожие презентации:
Методы исследований операций
1. Методы исследований операций
1. Однако при большом числе аргументов решениепо нахождению экстремума классическим
методом затруднено.
2. Кроме того, часто экстремум находиться не в
одной точке , а где-то рядом в определенной
области
Поэтому используются другие методы.
2. Оптимизация
1.Если целевая функция линейно зависит от решенийx1, x2 …xn и ограничения имеют вид линейных
равенств (неравенств) , то имеем задачу линейного
программирования.
2. При нелинейном программировании : N(x) , Q (x)
нелинейно зависит от параметров x1, x2 …xn3
3. Выбор решения в условиях неопределенности
Тогда целевая функция будет иметь вид
W=W (a , x , ε )
Где
a-условия (ограничения)
X- множество решений
ε – неизвестные факторы
3. Оптимизация
Если ε – случайные величины ( т.е. имеютраспределение ), то такую неопределенность наз.
Стохастической
Случайные величины и неопределенность – разные
вещи.
Случайные величины при большом числе повторений
становятся определенными.
Неопределенность – нет распределения.
Особую группу занимают МНОГОКРИТАРИАЛЬНЫЕ
МЕТОДЫ ОПТИМИЗАЦИИ
КАЧЕСТВО ПО характеризуется не одним , а
несколькими критериями («Эффективность»,
«Функциональность» и т.д.)
4. оптимизация
Такие задачи оптимизации наз многокритериальнымиДля оценки качества ПО используется метод
«Обобщенного показателя качества ПО» – метод
представляет собой «взвешенную сумму» частных
показателей
Каждый показатель имеет атрибуты Каждый атрибут
имеет метрики.
Тогда
Q= S1*W1 + S2* W2 + …
Где S1, S2 , - веса
Т.е. показатели (как и атрибуты) , которые надо
уменьшить берётся меньший вес, показатели которые
надо увеличить берется больший вес.
5. Линейное программирование
6.
7. примеры
8. Задача лин программирования
9. ии
10. Построение моделей задачи лин. программирования
Задача.Предприятие выпускает три вида продукции П1 , П2, П3 и
использует три типа сырья C1, C2, C3
Причем сырья С1 предприятие может израсходовать не более
32 т,
Сырья С2 – не более 35 тонн, С3 – не более 50 т.
Нормы расхода сырья на 1 единицу продукции приведены в
табл.
Сырье
запасы
П1
П2
П3
С1
32
2
3
0
С2
35
4
1
2
С3
50
3
1
3
4
5
8
Расходы
11. задача
Определить : количество продукции типа П1 , П2 , П3 приминимальных затратах.
Решение.
1.
Вводим обозначения для неизвестных величин.
Обозначим через x1, x2 , x3 – количество продукции типа П1, П2, П3.
2. Проанализируем ограничения и составим систему ограничений
2x1 + 3x2 ≤ 32
4x1 + x2+ 2x3 ≤35
3x1+ x2 + 3x3 ≤ 50
3 шаг. Составляем целевую функцию.
Т.к. целевая функция в данном примере – расходы ,
То получим
L(x)= 4x1 + 5x2 + 8 x3 → min
12. примеры
ЗадачаЕсть три прибора . Каждый прибор имеет
резисторы ( не более b1 – ограничение 1),
конденсаторов (не более b2 – ограничение 2),
микросхем (не более b3 – ограничение 3)
Тогда можно составить уравнение по 1
ограничению
a11 * x1 + a 21 * x2 + a 13 * x3 ≤ b1
1 прибор
2 прибор
3 прибор
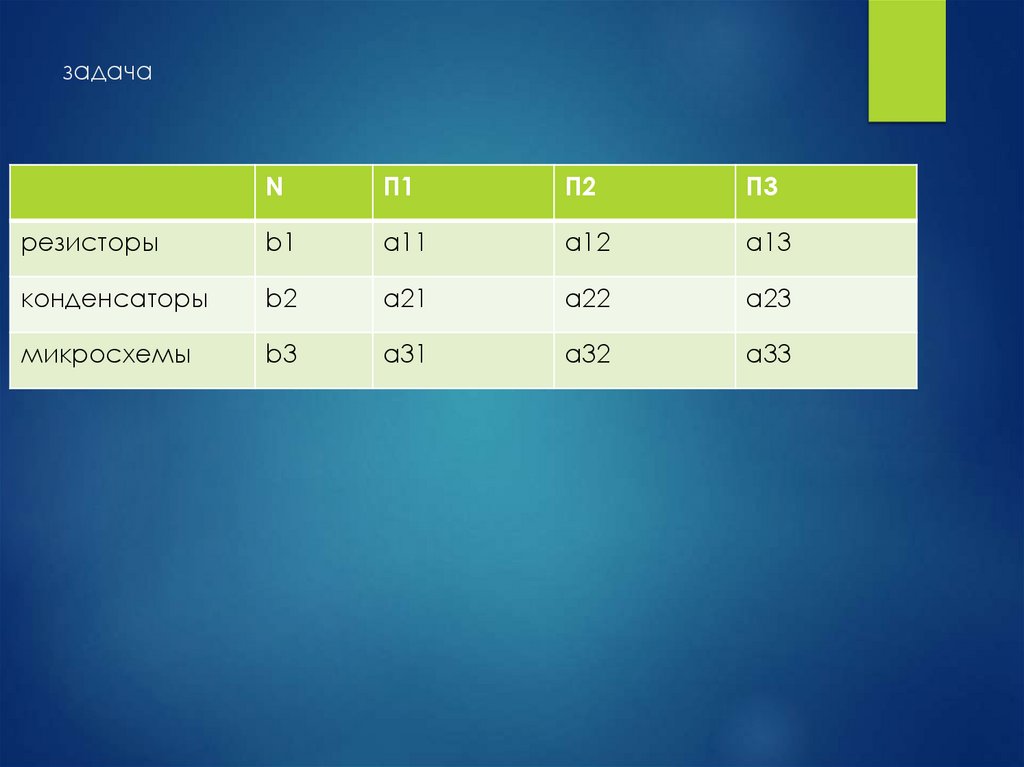
13. задача
NП1
П2
П3
резисторы
b1
a11
a12
a13
конденсаторы
b2
a21
a22
a23
микросхемы
b3
a31
a32
a33
14. задача
Тогда индекс i- принадлежность к строкам наименованиетипа элемента прибора(ннапр. 1 строка – резисторам)
Индекс j – определяет принадлежность конкретному
прибору(напр. 1 – прибору П1)
Тогда коэффициент a11 будет определять норматив
количества резисторов для 1 прибора, a 12 – для 2
прибора и т.д.)
Аналогично составляем для конденсаторов
a 21 x1 + a 22 x2 + a23 x3 ≤ b2
Для микросхем
a 31 x1 + a 32 x2 + a 33 x3 ≤ b3
15. Задача
16. задача
17. Методы решений
B. Уравнения совместны , но в области отрицательныхчисел.
С. Решения есть , но они не оптимальные.
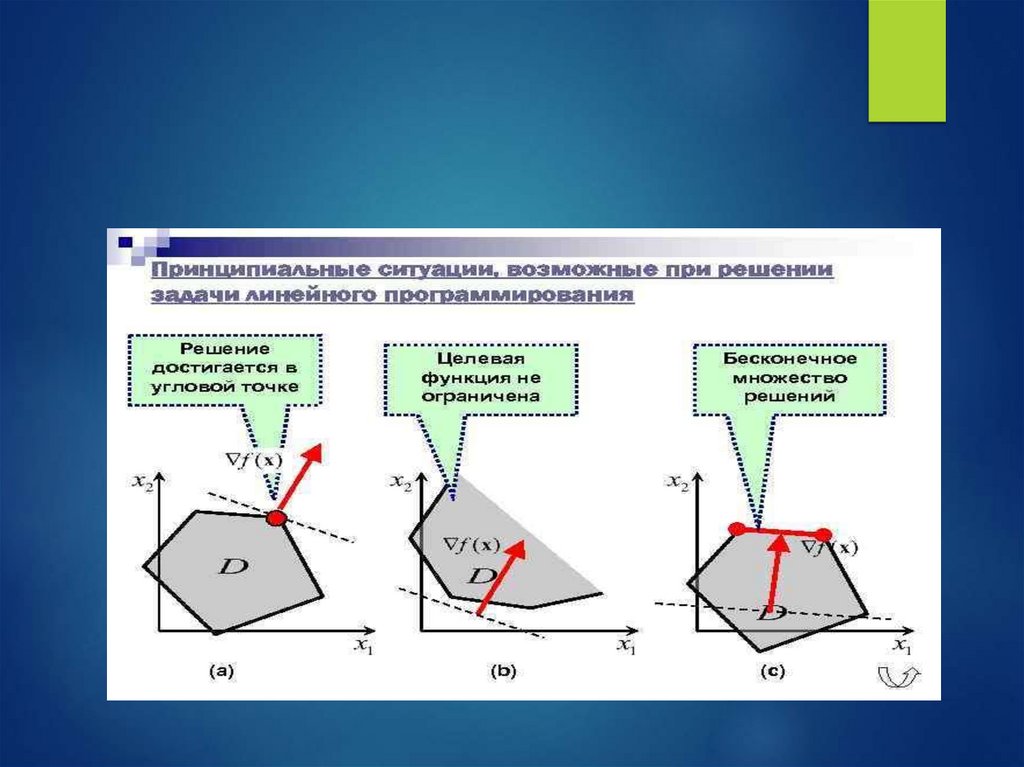
ГРАФИЧЕСКИЙ МЕТОД
1.
Строят ОДР (область допустимых решений)
2.
Примечания :
Если ОДР – пустое множество , то система не имеет
решения (ввиду несовместности системы ограничений).
Если ОДР неограничена по направлению вектора нормали
n= (c1 ; c2) , то сама целевая функция неограничена сверху
в этой области и принимаем
L max (x) cтремиться к бескончности, а Lmin к минус
бесконечности.
18. Строительство ОДР
Т.к. переменные должны быть неотрицательные тодопустимые значения
19.
20. .
Любая неканоническая форма может бытьприведена к канонической.
21.
22. оптимизация
Т.о. идут по функции пока не найдем экстремум.Т.о. алгоритм
Вводим границы интервалов поиска по
переменным, шаг перебора, целевую
функцию, ограничения
Находим количество шагов на сетке
23. примеры
.Цикл для n1 , n2
Счетчик
Вычисляем
Z(x1, x2)
Запоминаем значения координат x1, x2
Находим экстремум
(min z=z( x1, x2)






















 Математика
Математика








