Предмет, цели и задачи исследования операций. Основные определения. Математические модели исследования операций

1. План лекции

Предмет, цели и задачи исследования
операций
Основные определения
Математические модели исследования
операций
Разновидности задач и подходов к их решению

2. Исследование операций

Исследование операций связано с такими вопросами
как:
Математические методы оптимизации
Линейное , нелинейное программирование
Динамическое программирование

3. Исследование операций

Методы исследования операций используется в разных
областях практики:
Снабжения
Эксплуатация транспорта
Имеют место схожие ситуации имеющие общие признаки и
решаемые сходными методами
Есть мероприятие , надо принять решение оптимальное из
нескольких вариантов.
Не сразу можно определить какой вариант лучше. Чтобы
прояснить обстановку необходимо выполнить расчеты

4. Определения

Исследование операций – применение
математических методов, количественных
методов для обоснования принятия решения.
Т.о. решение – это обоснованный выбор
Впервые теория исследование операций
появилась в годы Второй мировой войны :
боевого применения оружия, сил и средств.п

5. Основные определения

Операцией – наз. Всякое мероприятие (система
действий) , объединенная единым смыслом.
Операция всегда управляемое мероприятие
Решение – обоснованный определенный выбор
Оптимальными называются решения по тем или иным
соображений являющиеся предпочтительными
Относительно редко можно выделить одно решение
Часто – можно выделить область решений

6. примеры

1. План снабжения предприятия
Есть сырьевые базы и есть предприятия потребляющие
сырье
Базы связаны с предприятиями сетью транспортных
магистралей(желез дорож., воздуш и т.д.)
Требуется : разработать план снабжения предприятий (т.е.
с какой базы , в каком количестве и какое сырье
доставляется

7. Конрекретизация для данного примера

Обозначим через
A1 , A2 , … Ai - исходные базы
B1 , B2, … Bj – предприятия
Тогда элементами решений будут числа показывающие
какое количество групп надо отправлять из пункта Ai в пункт
Bj
Т.е. имеем числа x11, x12 …xij

8. Оптимальное решение

При заданном комплексе условий a найти такое
решение x чтобы показатель эффективности W
обращался в max.
Примеры
Показателя эффективности
Доход - max
Т.о. типовая задача на экстремум

9. Экстремумы функций

10. Экстремумы

11. Экстремум функции двух переменных

12. Геометрический смысл частных производных

13. Экстремум двух переменных

14. Оптимальное решение

При заданном комплексе условий a найти такое
решение x чтобы показатель эффективности W
обращался в max.
Примеры
Показателя эффективности
Доход - max
Т.о. типовая задача на экстремум

15. векторы

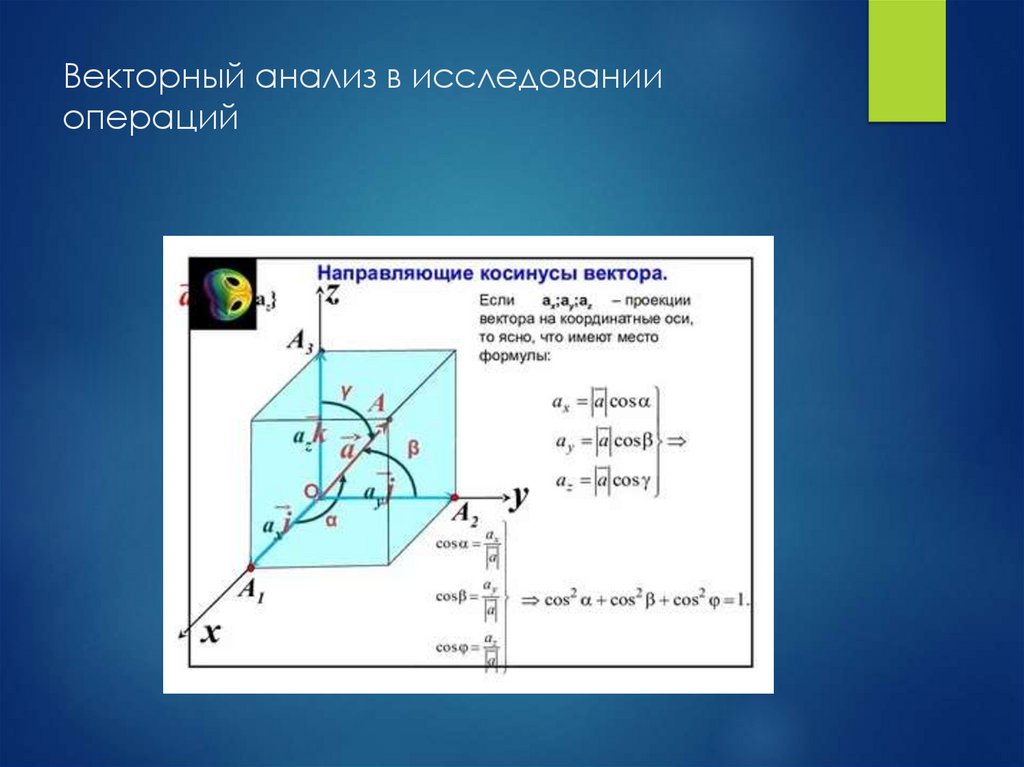
16. Векторный анализ в исследовании операций

17. .

18. .

19.

20. Оптимизация

1.Если целевая функция линейно зависит от решений
x1, x2 …xn и ограничения имеют вид линейных
равенств (неравенств) , то имеем задачу линейного
программирования.
2. При нелинейном программировании : N(x) , Q (x)
нелинейно зависит от параметров x1, x2 …xn3
3. Выбор решения в условиях неопределенности
Тогда целевая функция будет иметь вид
W=W (a , x , ε )
Где
a-условия (ограничения)
X- множество решений
ε – неизвестные факторы

21. Модели при анализе

При анализе ПО применяются
Аналитические модели
Статистические модели
Модели смешанного типа (Гоэл – Окимото)
Аналитические модели дают более общую оценку , учитывают
меньшее число факторов. Но аналитические модели более
приспособлены для поиска оптимального решения.
Статистические модели более точны , не требуют грубых
допущений , но трудно осуществлять поиск оптимальных
решений.
Построить модель и произвести расчеты – это только 1/ 3
работы. Главное – проанализировать результаты и перевести их
в ранг рекомендаций.

22. Математические модели в «исследовании операций»

Имитационное моделирование – относится к
процессам к которым время от времени
вмешивается человек.
Напр. Человек принимает решение .
Математическая модель показывает к каким
последствиям приведет это решение
Следующее решение принимается уже с
учетом опыта принятия предыдущих решений.
В результате принимается почти или близкое к
оптимальному решение(т.е. идет обучение)

23. Методы исследований операций

1. Однако при большом числе аргументов решение
по нахождению экстремума классическим
методом затруднено.
2. Кроме того, часто экстремум находиться не в
одной точке , а где-то рядом в определенной
области
Поэтому используются другие методы.

24. Методы исследований операций

1. Однако при большом числе аргументов решение по
нахождению экстремума классическим методом
затруднено.
2. Кроме того, часто экстремум находиться не в одной
точке , а где-то рядом в определенной области
Поэтому используются другие методы.

25. Оптимизация

1.Если целевая функция линейно зависит от решений
x1, x2 …xn и ограничения имеют вид линейных
равенств (неравенств) , то имеем задачу линейного
программирования.
2. При нелинейном программировании : N(x) , Q (x)
нелинейно зависит от параметров x1, x2 …xn3
3. Выбор решения в условиях неопределенности
Тогда целевая функция будет иметь вид
W=W (a , x , ε )
Где
a-условия (ограничения)
X- множество решений
ε – неизвестные факторы

26. Оптимизация

Если ε – случайные величины ( т.е. имеют
распределение ), то такую неопределенность наз.
Стохастической
Случайные величины и неопределенность – разные
вещи.
Случайные величины при большом числе повторений
становятся определенными.
Неопределенность – нет распределения.
Особую группу занимают МНОГОКРИТАРИАЛЬНЫЕ
МЕТОДЫ ОПТИМИЗАЦИИ
КАЧЕСТВО ПО характеризуется не одним , а
несколькими критериями («Эффективность»,
«Функциональность» и т.д.)

27. оптимизация

Такие задачи оптимизации наз многокритериальными
Для оценки качества ПО используется метод
«Обобщенного показателя качества ПО» – метод
представляет собой «взвешенную сумму» частных
показателей
Каждый показатель имеет атрибуты Каждый атрибут
имеет метрики.
Тогда
Q= S1*W1 + S2* W2 + …
Где S1, S2 , - веса
Т.е. показатели (как и атрибуты) , которые надо
уменьшить берётся меньший вес, показатели которые
надо увеличить берется больший вес.

28. Линейное программирование

29. примеры

30. Задача лин программирования

31. ии

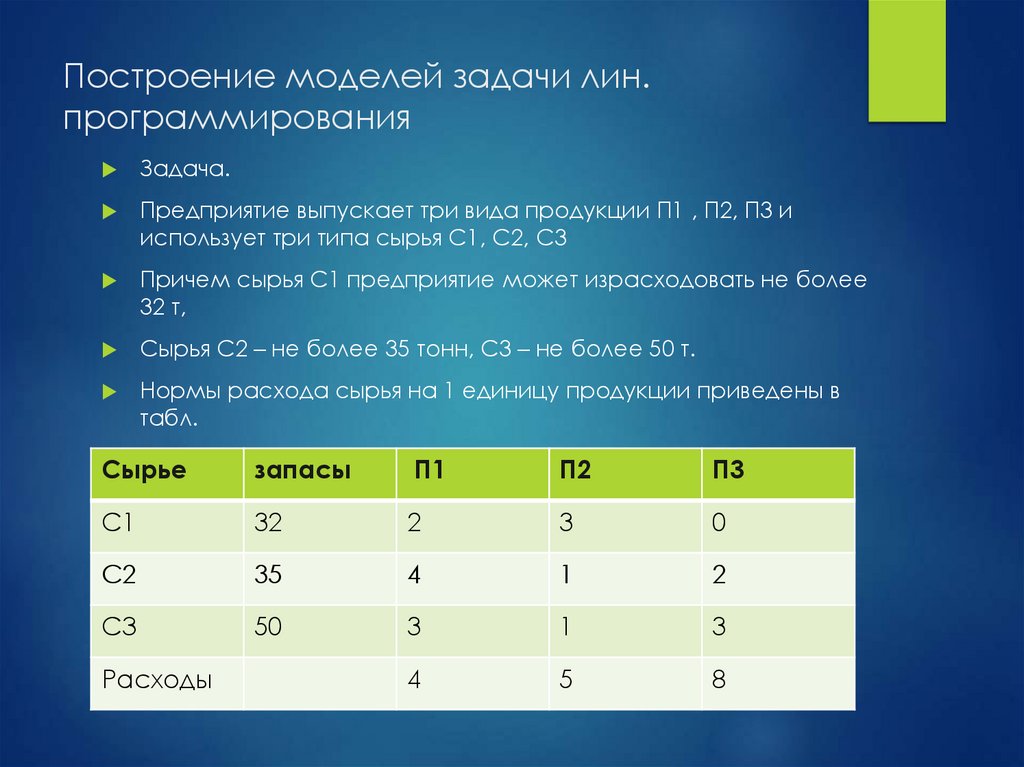
32. Построение моделей задачи лин. программирования

Задача.
Предприятие выпускает три вида продукции П1 , П2, П3 и
использует три типа сырья C1, C2, C3
Причем сырья С1 предприятие может израсходовать не более
32 т,
Сырья С2 – не более 35 тонн, С3 – не более 50 т.
Нормы расхода сырья на 1 единицу продукции приведены в
табл.
Сырье
запасы
П1
П2
П3
С1
32
2
3
0
С2
35
4
1
2
С3
50
3
1
3
4
5
8
Расходы

33. задача

Определить : количество продукции типа П1 , П2 , П3 при
минимальных затратах.
Решение.
1.
Вводим обозначения для неизвестных величин.
Обозначим через x1, x2 , x3 – количество продукции типа П1, П2, П3.
2. Проанализируем ограничения и составим систему ограничений
2x1 + 3x2 ≤ 32
4x1 + x2+ 2x3 ≤35
3x1+ x2 + 3x3 ≤ 50
3 шаг. Составляем целевую функцию.
Т.к. целевая функция в данном примере – расходы ,
То получим
L(x)= 4x1 + 5x2 + 8 x3 → min

34. примеры

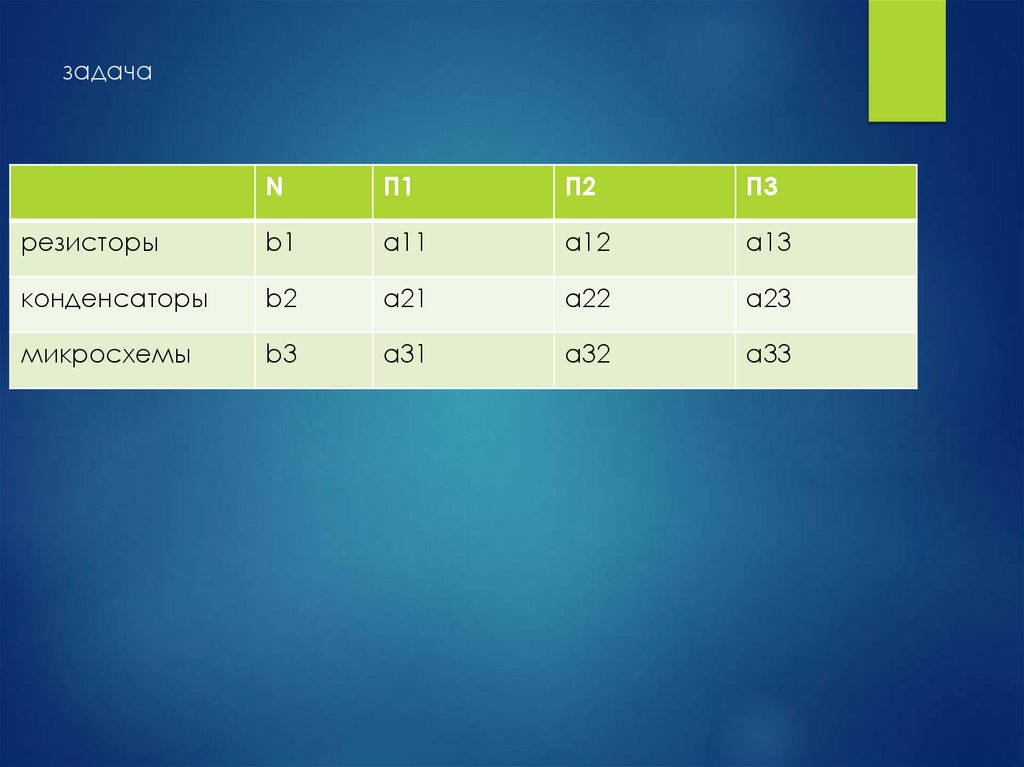
Задача
Есть три прибора . Каждый прибор имеет
резисторы ( не более b1 – ограничение 1),
конденсаторов (не более b2 – ограничение 2),
микросхем (не более b3 – ограничение 3)
Тогда можно составить уравнение по 1
ограничению
a11 * x1 + a 21 * x2 + a 13 * x3 ≤ b1
1 прибор
2 прибор
3 прибор

35. задача

N
П1
П2
П3
резисторы
b1
a11
a12
a13
конденсаторы
b2
a21
a22
a23
микросхемы
b3
a31
a32
a33