Метод наименьших квадратов. Лекция 15

1.

ПРАКТИЧЕСКАЯ ФИЗИКА
Доцент кафедры
экспериментальной физики
Ерина Марина Васильевна

2.

Лекция № 15
Метод наименьших квадратов

3.

Важной задачей обработки результатов эксперимента является нахождение
вида функциональной зависимости по данным эксперимента.
Допустим, в эксперименте изменяется величина x и в соответствии с этим
измеряется другая величина y, которая зависит от x. В результате получается
набор значений (x1;y1), (x2;y2), (x3;y3), (x4;y4), … (xn;yn).
Задача: Найти уравнение зависимости y(x),
соответствующее экспериментальным данным.
наилучшим
образом

4.

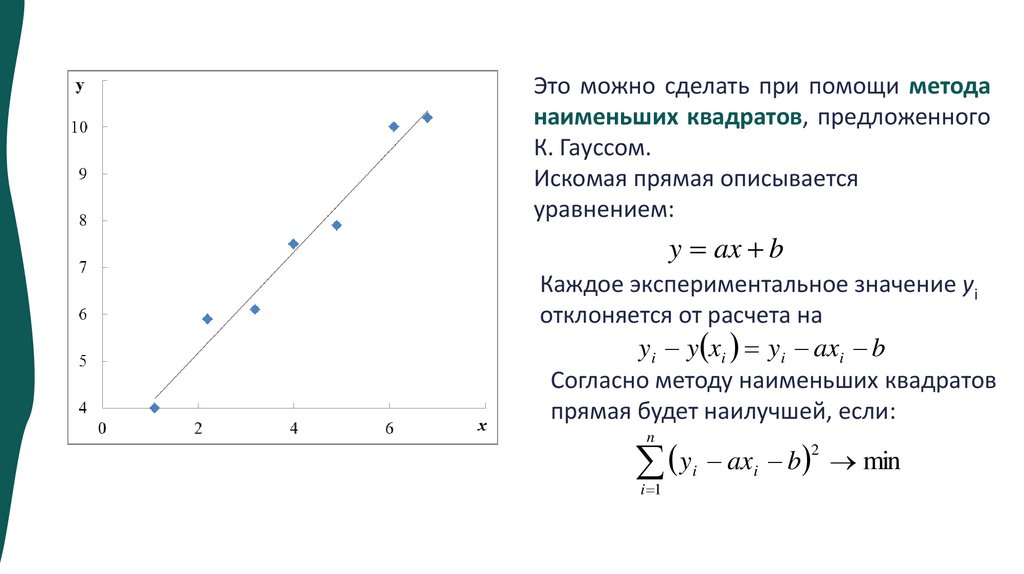
Это можно сделать при помощи метода
наименьших квадратов, предложенного
К. Гауссом.
Искомая прямая описывается
уравнением:
y ax b
Каждое экспериментальное значение yi
отклоняется от расчета на
yi y xi yi axi b
Согласно методу наименьших квадратов
прямая будет наилучшей, если:
n
2
y
ax
b
min
i i
i 1

5.

Задача сводится к нахождению таких a и b, при которых эта функция достигает
минимума.
F (a, b) yi axi b yi a 2 xi b 2 2ayi xi 2byi 2abxi
2
2
2
Находим частные производные по a и b, затем приравниваем их к нулю:
F (a, b) n
2
2axi 2 xi yi 2bxi 0
a
i 1
Составляем и решаем систему:
F (a, b) n
2b 2 yi 2axi 0
b
i 1
a xi 2 b xi xi yi
a xi nb yi

6.

xi
x
x n
2
i
n
i
x x
2
2
i
i
x y x
n x y x y
y n
i
i
i
a
i
i
i
i
i
b
xi
x
i
2
x y x y x x y
y
i
i
2
i
i
i
i
i
i
a n xi y i x i y i
a
2
2
n xi xi
b
b
xi yi xi xi yi
2
n xi xi
2
2

7.

Погрешности в величинах a и b
Для нахождения погрешности в величинах a и b найдем стандартное отклонение
значений y:
y
2
1 n
2
y
ax
b
i
i
n 2 i 1
Множитель 1/(n-2) говорит о том, что если есть две точки, то через них всегда
можно провести прямую, притом единственную, т.е. ни о каких ошибках
говорить не приходится.
y xi
2
a2
2
b2
n y
2

8.

Пример оформления таблицы для МНК:
n
1
2
3
х
y
x2
x∙y
∑x
(∑x)2
∑y
∑x2
∑(x∙y)
4
5
…

9.

Пример:
Используйте МНК, чтобы определить линию у=aх+b, которая наилучшим
образом аппроксимирует четыре точки: (1;12), (2;13); (3;18), (4;19). Постройте
точки и линию.
n
1
2
х
y
x2
x∙y
1
2
12
13
1
12
4
26
3
4
3
4
18
19
9
54
16
76
30
168
10
x 100
2
62
4 168 10 62
a
2,6
4 30 100
b
30 62 10 168
9
4 30 100
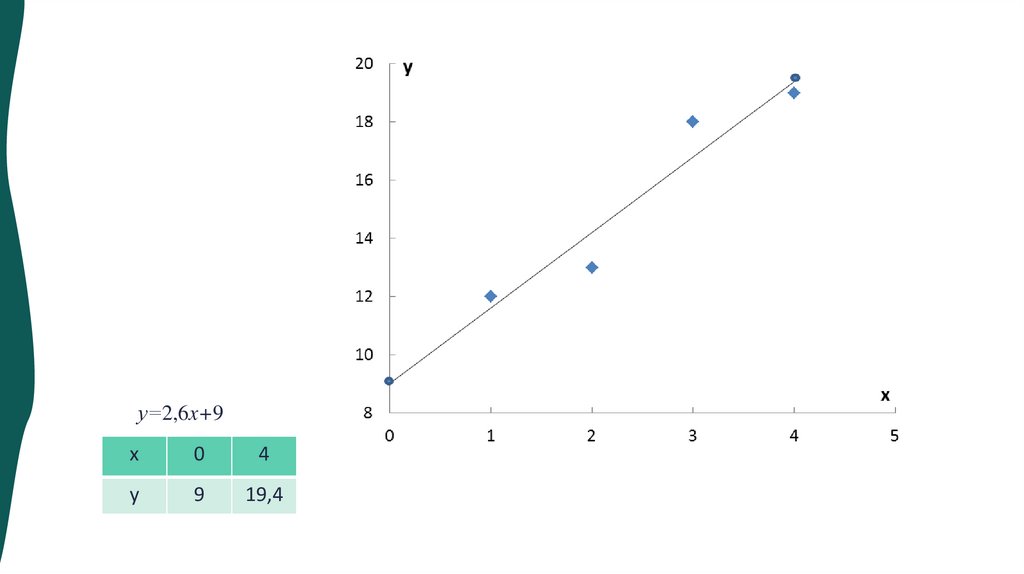
у=aх+b=2,6x+9

10.

у=2,6x+9
х
0
4
у
9
19,4

11.

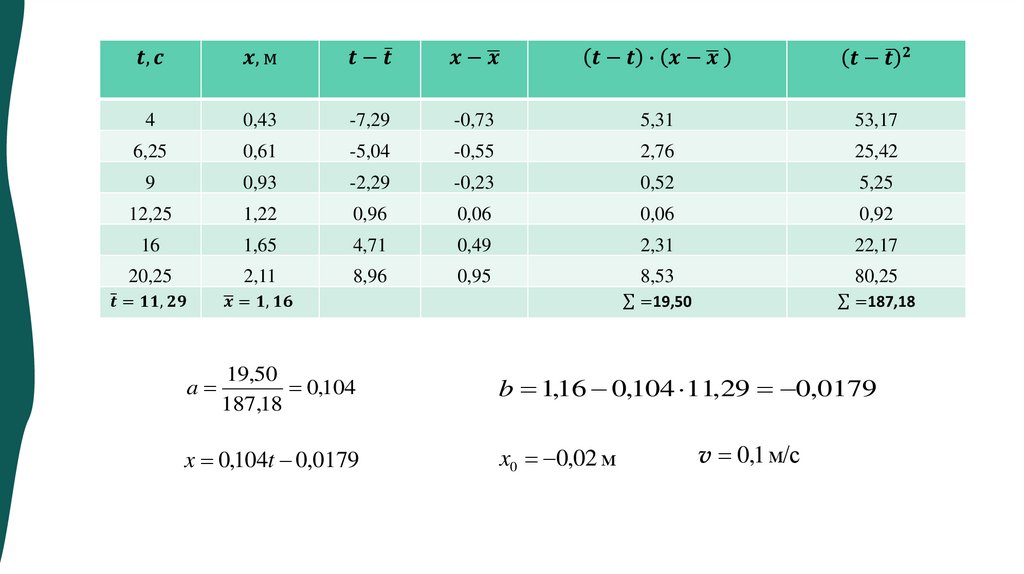
Метод наименьших квадратов (2 способ)
y ax b
x x y y
a
x x
i
i
2
b y ax
i
Пример оформления таблицы для МНК (2 способ):