Метод наименьших квадратов

1.

Справочный материал к практике 15 по
дисциплине «Математика» для студентов
направления подготовки
09.03.02 «Информационные системы и
технологии»
Метод наименьших квадратов
Составитель:
ст. преподаватель кафедры «Физикоматематические науки» Черемухин А. Д.

2.

МНК и линейная регрессия
Дано: много-много точек (реальных данных) Допустим, функция линейна (ну видно же). Т.е., y = ax+b (а и b, увы, мы не
знаем). Таким образом, зная координаты точек (х;y), надо найти а и b.
Способ: МНК (метод наименьших квадратов)
a
Задача: найти уравнение функции y = f(x),
описывающее эти точки (с погрешностью)
n
n
n
i 1
i 1
i 1
n xi yi xi yi
n xi2 xi
i 1
i 1
n
n
2
n
1 n
b yi a xi .
n i 1
i 1
,

3.

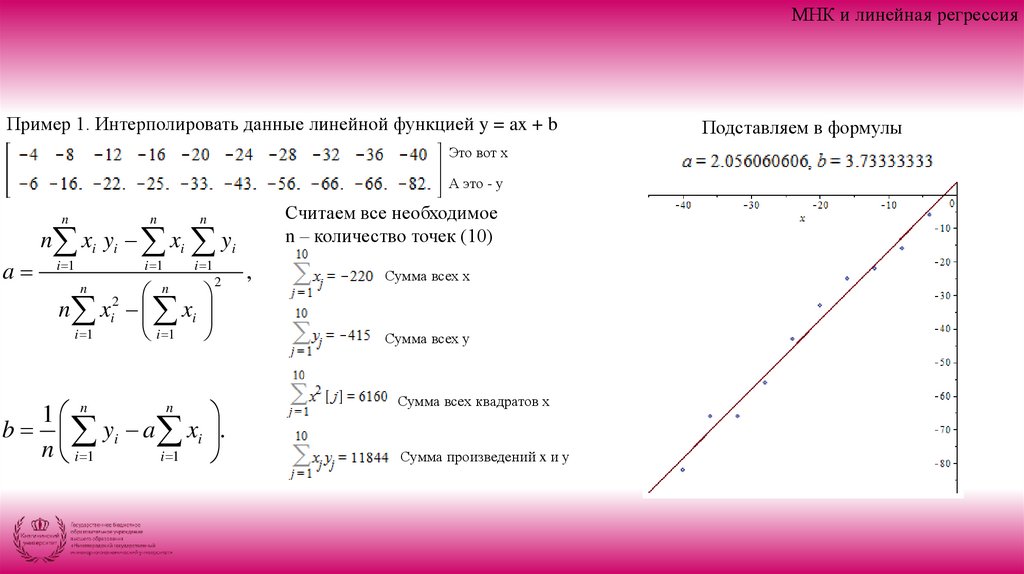
МНК и линейная регрессия
Пример 1. Интерполировать данные линейной функцией y = ax + b
Это вот х
А это - у
a
n
n
n
i 1
i 1
i 1
Считаем все необходимое
n – количество точек (10)
n xi yi xi yi
n x xi
i 1
i 1
n
n
2
,
Сумма всех х
2
i
n
1 n
b yi a xi .
n i 1
i 1
Сумма всех у
Сумма всех квадратов х
Сумма произведений x и у
Подставляем в формулы

4.

МНК и линейная регрессия
Пример 2. Интерполировать данные функцией
В случае, если функция нелинейна, необходимо сделать замену переменных и свести все к нахождению линейной
системы.
В нашем случае
Необходимо преобразовать данные
И по ним все посчитаем