Параллельные алгоритмы

1.

Параллельные алгоритмы
1

2.

Moore's Law
T
r
a
n
s
i
s
t
o
r
c
o
u
n
t
Year of introduction
2

3.

Закон Мура и прогноз Дэвида Хауса(from Intel)
Соучредитель Fairchild Semiconductor
генеральный директор Intel
2004 - 75 место в списке богатейших людей планеты по
версии журнала Forbes.
Gordon Moore
Количество транзисторов, размещенных на микросхеме интегральной схемы,
удваивается каждые 24 месяца.
Закон Мура — эмпирическое наблюдение (не физический или естественный
закон), сделанное Гордоном Муром в 1965 году.
Производительность процессора должна удваиваться каждые 18 месяцев за
счет:
роста числа транзисторов
увеличение тактовой частоты процессоров
3

4.

Будущее закона Мура
● Большинство прогнозистов полупроводниковой отрасли, включая
Гордона Мура, ожидают, что закон Мура перестанет действовать
примерно к 2025 году. Почему?
4

5.

Кризис эффективности
● Благодаря Закону Мура - увеличение производительности все время
приводило к уменьшению времени выполнения некоторой задачи.
● Ответ на предел тактовой частоты - многопроцессорные системы.
● Последовательные программы не могут работать на
многопроцессорных системах быстрее, чем на последовательных.
● Необходима разработка новых алгоритмов использующих преимущества
современного “железа”.
● Автоматически преобразовать последовательные программы в
параллельные не эффективно, а часто и невозможно.
5

6.

Определение
Параллельный алгоритм - алгоритм, который может быть реализован по
частям на множестве различных вычислительных устройств с последующим
объединением полученных результатов и получением корректного
результата
6

7.

Параллельные алгоритмы
Причины использования параллельных алгоритмов:
1. Сокращение времени решения прикладных задач (Amdahl's Law (1967))
2. Возможность решения больших задач за заданное время (Gustafson –
Barsis's law (1988)). Эту характеристику называют ускорением
масштабирования (scaled speedup), т.к. она показывает, насколько
эффективно могут быть организованы параллельные вычисления при
увеличении сложности решаемых задач.
7

8.

Amdahl's Law (1967)
American scientist in the field of computer
technology, a mathematician and
businessman,
best known for his work in the company
of the IBM, and then founded the
company Amdahl Corporation .
1922-2015
8

9.

Gustafson – Barsis's law (1988)
John Leroy Gustafson (born January 19, 1955) is an
American computer scientist and businessman, chiefly
known for his work in High Performance
Computing (HPC)
Main idea:
Speedup can be regarded as an increase in the
volume problem for constant time interval !
N - number of processors, s - serial fraction.
9

10.

Масштабируемость параллельных
программ
Strong Scaling
Amdahl's Law
Weak Scaling
Gustafson–Barsis's Law
10

11.

Масштабируемость параллельных программ
Существует два различных типа масштабирования:
• Strong Scaling – (сильное масштабирование) общий размер задачи
остается прежним по мере увеличения числа процессоров
• Weak Scaling – (слабое масштабирование) размер задачи увеличивается с
той же скоростью, что и количество процессоров, при этом объем работы на
процессор остается прежним.
Сильное масштабирование, как правило, более полезно и труднее для
достижения, чем слабое масштабирование.
11

12.

Идеальный параллельный алгоритм
Чем отличается параллельных алгоритм от последовательного?
В последовательном алгоритме нет накладных расходов:
● Синхронизация
● Обмен данными
● Дублирование операций
12

13.

Идеальный параллельный алгоритм
Идеальный параллельный алгоритм обладает следующими свойствами:
● Есть возможность одновременного выполнения операций (запас
параллелизма)
● Допускает возможность равномерного распределения вычислительных
операций между процессорами
● Обладает низким уровнем накладных расходов
13

14.

Граф алгоритма
Согласно классическому определению, любой (детерминированный)
алгоритм представляет собой последовательность шагов (операций),
однозначно определенную входными данными
14

15.

Последовательный алгоритм
Рассмотрим пример:
X = (a + b) * (c + d)
С одной стороны шаги 1 и 2 можно выполнить в другом порядке, а с другой стороны
их можно выполнить одновременно
15

16.

Параллельный алгоритм
16

17.

Граф алгоритма
Для описания параллельных алгоритмов необходима модель, учитывающая
как возможность параллельного выполнения операций, так и возможность
изменения последовательности выполнения. Простейшей моделью такого
рода является граф алгоритма (см., например, Bertsekas and Tsitsiklis
(1989), Воеводин В.В. и Воеводин Вл.В. (2002))
Для уменьшения сложности материала при построении модели будет
предполагаться:
● что время выполнения любых вычислительных операций является
одинаковым и равняется 1 (в тех или иных единицах измерения).
● передача данных между вычислительными устройствами выполняется
мгновенно без каких-либо затрат времени.
17

18.

Граф алгоритма
Граф алгоритма G(V,E) — это ориентированный граф, вершинами которого
являются операции алгоритма. Две операции u и v соединены дугой (u,v),
если в операции v используется результат выполнения операции u.
18

19.

Пример: Вычисление площади прямоугольника
19

20.

Граф алгоритма
Каждый ярус представляет собой итерацию в параллельном алгоритме, а каждая вершина
одного яруса представляет собой операцию, которая может быть выполнена параллельно
20

21.

Граф алгоритма
Для рассматриваемого примера можно выбрать разные параллельные
алгоритмы решения задачи, т.е. могут быть использованы разные схемы
вычислений и построены соответственно разные вычислительные модели.
Можно было просто формулу S = (x2-x1) * (y2 - y1).
Тогда нужно не 4, а 2 процессора.
Вопрос: как понять, что мы выбрали лучший алгоритм - нужны метрики –
показатели эффективности параллельного алгоритма.
21

22.

Основные показатели эффективности параллельного алгоритма
● Ускорение
● Эффективность
● Стоимость
22

23.

Ускорение
Ускорение (speedup), получаемое при использовании параллельного
алгоритма для P процессоров, по сравнению с последовательным
вариантом выполнения вычислений определяется величиной
n – параметр вычислительной сложности решаемой задачи (например,
количество входных данных задачи).
23

24.

Эффективность
Эффективность (efficiency) использования параллельным алгоритмом
процессоров при решении задачи определяется соотношением
Эффективность параллельного алгоритма показывает долю времени, в
течение которого один процессор в среднем занят вычислениями (остальное
время он простаивает).
24

25.

Стоимость
При выборе надлежащего параллельного способа решения задачи может
оказаться полезной оценка стоимости (cost) вычислений, определяемой как
произведение времени параллельного решения задачи и числа
используемых процессоров.
25

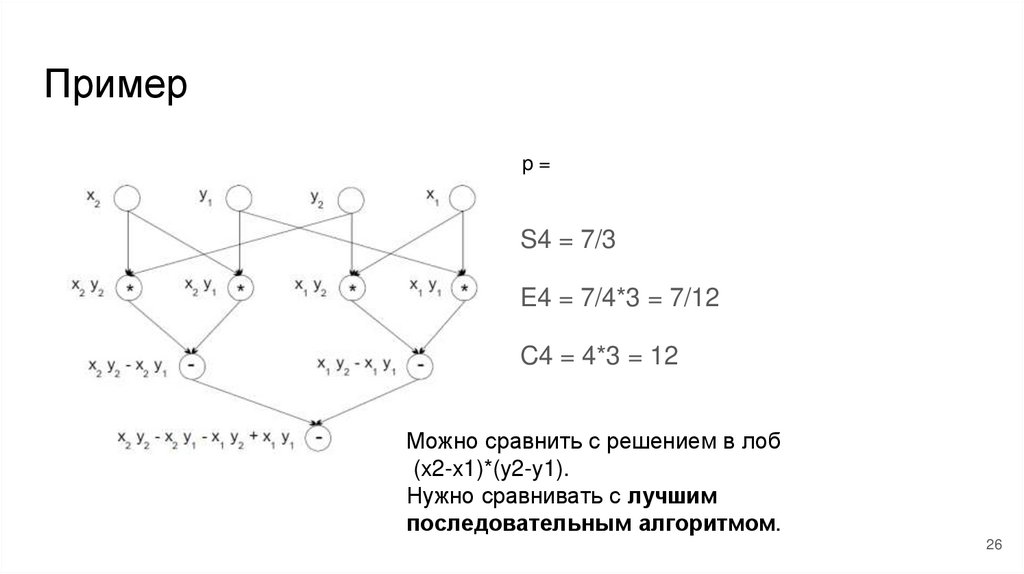
26.

Пример
p=
S4 = 7/3
E4 = 7/4*3 = 7/12
C4 = 4*3 = 12
Можно сравнить с решением в лоб
(x2-x1)*(y2-y1).
Нужно сравнивать с лучшим
последовательным алгоритмом.
26

27.

Оценка максимально достижимого параллелизма
1
1
1
1
1
Ускорение:
S = 5/1 = 5
27

28.

Оценка максимально достижимого параллелизма
1
1
1
1
2
Ускорение:
S=?
28

29.

Закон Амдала
Sp - ускорение
α - доля последовательного кода
p - количество процессоров
1. Чем больше α тем меньше ускорение
2. Прирост эффективности вычислений
зависит от алгоритма задачи и ограничен
сверху для любой задачи с α = 0
3. Чем больше кода для синхронизации
тем меньше ускорение
29

30.

Оценка максимально достижимого параллелизма
1
1
1
1
2
Ускорение:
1/S = 1/6 + 5/(6*5) = 1/3
S=3
Какое ускорение будет для десятерых моляров и десяти комнат одна из которых в
два раза больше другой?
Ответ: 1/S = 1/11 + 1/11, S = 5.5
30

31.

Оценка максимально достижимого параллелизма
Как определить качество
параллельного алгоритма?
S=p и E=1
Идеальный вариант не достижим на
практике.
Поэтому алгоритм считается эфективным,
ускорение которого, по крайней мере,
ограничена некоторой константой, а не
стремится к нулю с ростом n и p.
31

32.

Закон Амдала
32

33.

Пример. Задача вычисления общей суммы
Традиционный алгоритм для решения этой задачи
состоит в последовательном суммировании
элементов числового набора:
33

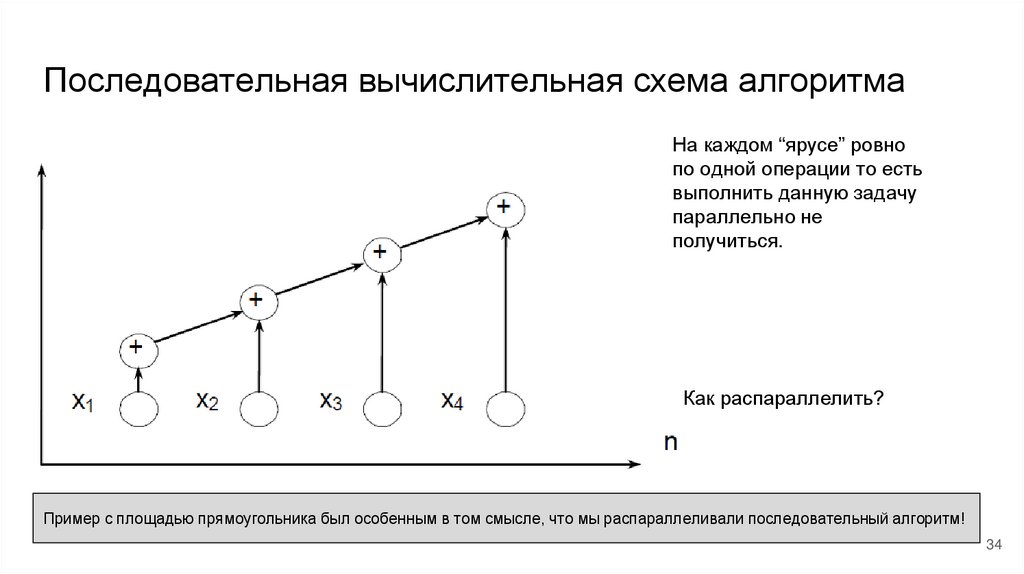
34.

Последовательная вычислительная схема алгоритма
На каждом “ярусе” ровно
по одной операции то есть
выполнить данную задачу
параллельно не
получиться.
Как распараллелить?
Пример с площадью прямоугольника был особенным в том смысле, что мы распараллеливали последовательный алгоритм!
34

35.

Каскадная схема суммирования
Параллелизм алгоритма суммирования возможен только при ином способе
построения процесса вычислений, основанном на использовании
ассоциативности операции сложения:
-
-
на первой итерации каскадной схемы все исходные данные
разбиваются на пары, и для каждой пары вычисляется сумма их
значений,
далее все полученные суммы также разбиваются на пары, и снова
выполняется суммирование значений пар и т.д.
35

36.

Каскадная схема алгоритма суммирования
n = 2k
Общее количество итераций:
Общее количество операций
суммирования:
Сколько нужно процессоров чтобы выполнить данный
алгоритм с максимальным параллелизмом?
p = n/2
Общее количество параллельных
операций - ?
Kпар = log2n
36

37.

Показатели ускорения и эффективности
Эффективность использования процессоров уменьшается при увеличении количества
суммируемых значений
37

38.

Модифицированная каскадная схема
Получение асимптотически ненулевой эффективности может быть
обеспечено, например, при использовании модифицированной каскадной
схемы (см., Bertsekas and Tsitsiklis (1989), Воеводин В.В. и Воеводин Вл.В. (2002)). :
38

39.

Модифицированная каскадная схема
39

40.

Модифицированная каскадная схема
Для выполнения первого этапа требуется параллельных операций:
При использовании