Похожие презентации:
Логические основы построения цифровых автоматов
1.
Логические основы построения цифровыхавтоматов
2.
• Основу любого дискретного вычислительногоустройства составляют элементарные логические
схемы. Работа этих схем основана на законах и
правилах алгебры логики, которая оперирует двумя
понятиями: истинности и ложности высказывания.
• Алгебра логики — раздел математики, изучающий
высказывания, рассматриваемые со стороны их
логических значений (истинности или ложности) и
логических операций над ними. Высказывание —
некоторое предложение, в отношении которого
можно однозначно сказать, истинно оно или ложно.
3.
• Впервые практическое применение булевой алгебрыбыло сделано К. Шенноном в 1938 г. для анализа и
разработки релейных переключательных сетей,
результатом чего явилась разработка метода
представления любой сети, состоящей из совокупности
переключателей и реле, математическими выражениями
и принципов их преобразования на основе правил
булевой алгебры [1]. Ввиду наличия аналогий между
релейными и современными электронными схемами
аппарат булевой алгебры нашел широкое применение для
их структурно-функционального описания, анализа и
проектирования.
4.
• Использование булевой алгебры позволяет не только болееудобно оперировать с булевыми выражениями
(описывающими те или иные электронные узлы), чем со
схемами или логическими диаграммами, но и на формальном
уровне путем эквивалентных преобразований и базовых
теорем упрощать их, давая возможность создавать
экономически и технически более совершенные электронные
устройства любого назначения. Операции булевой алгебры
часто встречаются и в программном обеспечении
вычислительных устройств, где они используются для замены
аппаратной логики на программную. Аппарат булевой алгебры,
как и любая другая формальная математическая система
состоит из трех множеств: элементов, операций над ними и
аксиом.
5.
Элементы.Схемы вычислительных устройств можно условно разделить на три группы:
исполнительные, информационные и управляющие.
Первые производят обработку информации, представленной в бинарной форме;
вторые служат для передачи бинарной формы информации;
третьи выполняют управляющие функции, генерируя соответствующие сигналы.
Во всех случаях в тех или иных точках логических схем сигналы двух различных
уровней могут представляться бинарными символами {0,1} или логическими
значениями {Истина (True), Ложь (False)}. Поэтому множество элементов булевой
алгебры выбирается бинарным В ={0,1}, а сама алгебра называется бинарной, или
переключательной. Ее элементы называются константами, или логическими 0 и 1,
которым в ряде случаев соответствуют бинарные цифры, в других случаях —
логические значения, соответственно ложь (False) и истина (True). В дальнейшем
для обозначения булевых переменных будем использовать буквы латинского
алфавита — х, у, z... . Набор переменных х, у, z...может рассматриваться как nразрядный двоичный код, разрядами которого являются эти переменные.
6.
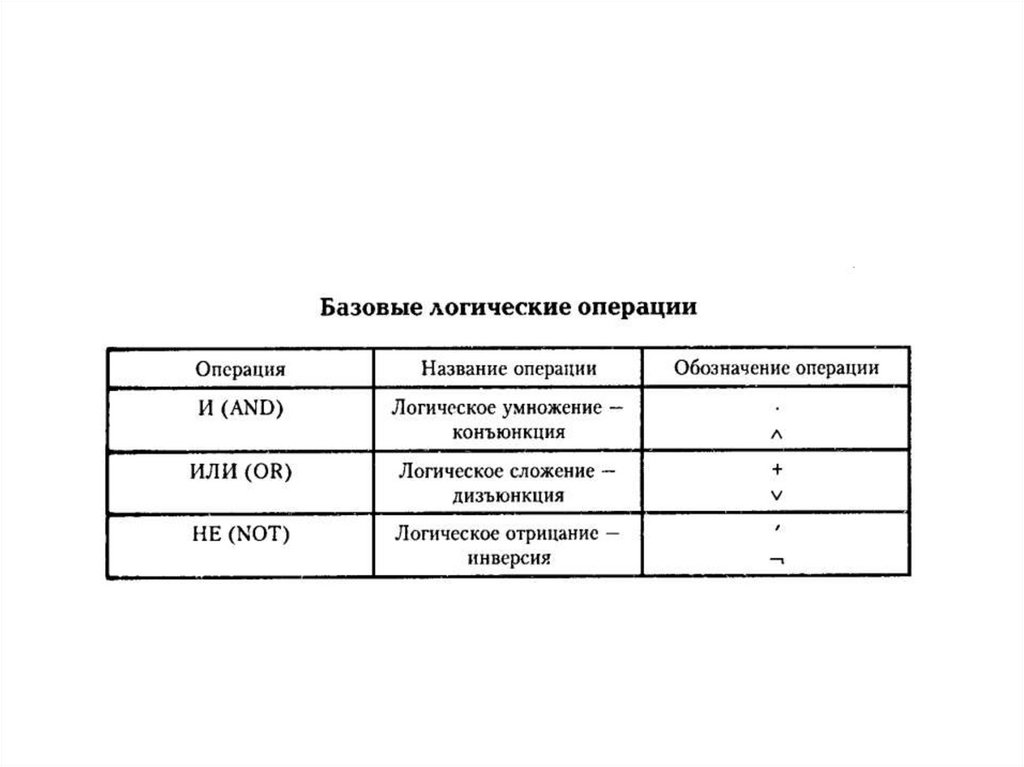
Операции• Основными, или базовыми, операциями булевой
алгебры служат: И (AND), ИЛИ (OR) и НЕ (NOT).
• Операция И называется логическим умножением или
конъюнкцией и обозначается знаком умножения
.
• Операция ИЛИ называется логическим сложением
или дизъюнкцией и обозначается знаком сложения {
+, v}.
• Операция НЕ называется логическим отрицанием или
инверсией (дополнением) и обозначается знаком
.
7.
8.
• При выполнении операций применяютсяотношение эквивалентности « = » и скобки
«()», которые определяют порядок
выполнения операций.
• Если скобок нет, то операции выполняются
в следующей последовательности:
логическое отрицание, логическое
умножение и логическое сложение
9.
Аксиомы• Булева алгебра базируется на нескольких аксиомах,
из которых выводят основные законы для
преобразований с двоичными переменными.
Обоснованность выбора этих аксиом подтверждается
таблицами истинности для рассмотренных операций.
Каждая аксиома представлена в двух видах, что
вытекает из принципа дуальности (двойственности)
логических операций, согласно которому операции
конъюнкции и дизъюнкции допускают взаимную
замену, если одновременно поменять логическую 1
на 0, 0 на 1.
10.
11.
12.
13.
14.
15.
16.
ПРЕДСТАВЛЕНИЕ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИБулевой (переключательной, двоичной) функцией называется двоичная
переменная у, значение которой зависит от значений других двоичных
переменных (х1, х2 ...,хn),
именуемых аргументами: у = у(х1, х2....................хn).
Задание булевой функции означает, что каждому из возможных сочетаний
аргументов поставлено в соответствие определенное значение у.
При n аргументах общее число сочетаний N = 2n .
Так как каждому сочетанию аргументов соответствует два значения функции
(О, 1), то общее число функций F = 22^n.
Булевая функция может быть задана на словах, таблично, алгебраически или
числовым способом.
17.
• В таблице представлена функция однойпеременной у = у(х). При n = 1 существует 4
функции, каждая из которых имеет свое
название.
18.
• Операцию замены одной функции другимифункциями называют суперпозицией. Эта операция
дает возможность с помощью функций малых
аргументов получить функции большего числа
аргументов. Так, при помощи суперпозиции можно
получить функцию с требуемым числом аргументов,
используя только функцию двух аргументов.
19.
• Рассмотрим функцию двух аргументов. Поопределению существует 16 функций двух
аргументов . При помощи набора булевых
функций двух аргументов можно описать
любую цифровую систему. На практике
используют не все функции, а лишь те из
них, которые методом суперпозиции
обеспечивают представление любой другой
функции
20.
21.
• Набор таких функций называют функционально полным набором(ФПН).
• Существует несколько ФПН. В качестве ФПН применяются
дизъюнкция, конъюнкция и инверсия. Этот набор называют
основным ФПН (ОФПН).
• Кроме ОФПН, широкое применение получили:
■ функционально-полная система, включающая в себя только одну
функцию — функцию Пирса (ИЛИ-НЕ);
■ функционально-полная система, включающая в себя только одну
функцию — функцию Шеффера (И-НЕ).
При помощи этих функций можно построить любую цифровую
систему. Синтез логических устройств в базисе ОФПН состоит из
представления этих функций в нормальных формах и минимизации.
22.
Нормальной формой считаютпредставление этих функций посредством
суперпозиций вспомогательных функций —
минтермов и макстермов.
• Минтермом называют функцию, которая
принимает 1 только при одном значении
аргументов и 0 — при других (иногда в
литературе используется термин
«конституэнта единицы»).
23.
• Например, для функции двух аргументовимеем:
• Таким образом, для функции двух
аргументов имеем четыре
24.
Макстермом называют функцию, которая принимает 0 только при одномзначении аргументов и 1 — при другом (иногда в литературе используется
термин «конституэнта ноля»). Например, для функции двух аргументов
имеем:
Таким образом, для функции двух аргументов имеем также
четыре макстерма:
25.
При этом, минтерм есть инверсия макстерма:26.
Форму представления функций посредством суперпозиции их минтермовназывают формой представления посредством совершенных
дизъюнктивных нормальных форм (СДНФ),
а посредством суперпозиции макстермов — посредством совершенных
конъюнктивных нормальных форм (СКНФ).
В общем случае форма представления функций посредством
суперпозиции их минтермов имеет вид:
27.
28.
29.
Любую функцию можно представить путем суперпозиции их минтермов(СДНФ) или макстермов (СКНФ).
Пример. Представим функцию Шеффера путем суперпозиции минтермов
(СДНФ) и макстермов (СКНФ).
Табличное представление функции Шеффера имеет
вид
30.
31.
ЛОГИЧЕСКИЙ СИНТЕЗ ПЕРЕКЛЮЧАТЕЛЬНЫХ И ВЫЧИСЛИТЕЛЬНЫХ СХЕМСинтез переключательных схем
В вычислительных и других автоматических устройствах широко применяются
электрические схемы, содержащие множество переключательных элементов: реле,
выключателей и т. п. При разработке таких схем с успехом может быть использован
аппарат алгебры логики.
Переключательная схема — схематическое изображение некоторого устройства,
состоящего из переключателей и соединяющих их проводников, а также входов и
выходов, на которые подается и с которых снимается электрический сигнал. Каждый
переключатель имеет только два состояния: замкнутое и разомкнутое.
Переключателю X поставим в соответствие логическую переменную х, которая
принимает значение 1 только в том случае, когда переключатель X замкнут и схема
проводит ток; если же переключатель разомкнут, то переменная х равна нолю. При
этом два переключателя X и X связаны таким образом, что когда X замкнут, то
X разомкнут, и наоборот. Следовательно, если переключателю X поставлена в
соответствие логическая переменная х, то переключателю X должна
соответствовать переменная х.
32.
Всей переключательной схеме также можно поставить в соответствие логическуюпеременную, равную единице, если схема проводит ток, и равную нолю — если
не проводит. Эта переменная является функцией от переменных,
соответствующих всем переключателям схемы, и называется функцией
проводимости.
Рассмотрим функции проводимости F некоторых переключательных схем:
а) Схема не содержит переключателей и проводит ток всегда, следовательно, F=
1;
б) Схема содержит один постоянно разомкнутый контакт, следовательно, F= 0;
в) Схема проводит ток, когда переключатель х замкнут, и не проводит, когда х
разомкнут, следовательно, F (х)=х;
г) Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда х
замкнут, следовательно, F (х)=х;
33.
г) Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда хзамкнут, следовательно, F (х)= х; Схема проводит ток, когда оба переключателя
замкнуты, следовательно, F(x)=х*у,
е) Схема проводит ток, когда хотя бы один из переключателей замкнут,
следовательно, F(x)= xvy.
При рассмотрении переключательных схем решают, как правило, одну из
основных задач: синтез или анализ схемы.
34.
Синтез переключательной схемы по заданным условиям ее работы сводится кследующим трем этапам:
1. Составление функции проводимости по заданным условиям.
2. Упрощение этой функции.
3. Построение соответствующей схемы.
Анализ схемы характеризуется следующими этапами:
1. Определение значений функции проводимости при всех возможных наборах
входящих в эту функцию переменных.
2. Получение упрощенной формулы.
35.
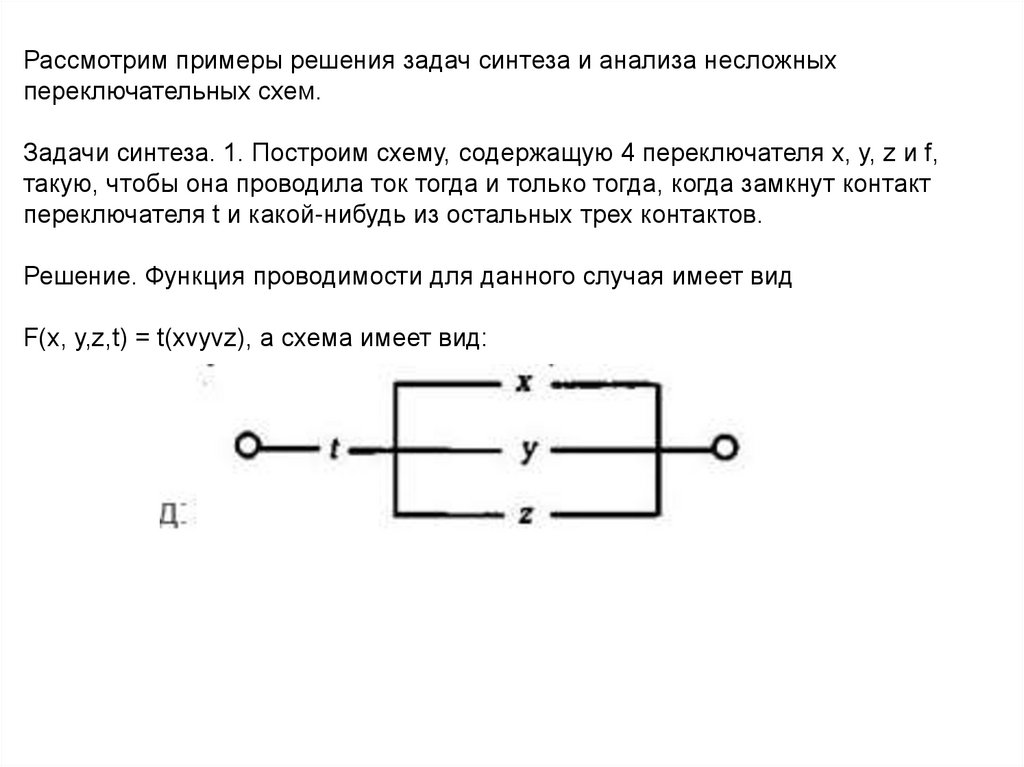
Рассмотрим примеры решения задач синтеза и анализа несложныхпереключательных схем.
Задачи синтеза. 1. Построим схему, содержащую 4 переключателя х, у, z и f,
такую, чтобы она проводила ток тогда и только тогда, когда замкнут контакт
переключателя t и какой-нибудь из остальных трех контактов.
Решение. Функция проводимости для данного случая имеет вид
F(x, y,z,t) = t(xvyvz), а схема имеет вид:
36.
2. Построим схему с пятью переключателями, которая проводит ток в том итолько в том случае, когда замкнуты ровно четыре из этих переключателей.
Решение: Схема имеет вид:
37.
38.
39.
40.
Синтез вычислительных схемТаблица истинности — табличное представление вычислительной
(логической) схемы (операции), в котором перечислены все
возможные сочетания значений истинности входных сигналов
(операндов) вместе со значением истинности выходного сигнала
(результата операции) для каждого из этих сочетаний.
Синтез вычислительных схем по заданным условиям работы сводится к
следующим трем этапам:
1. Образование СДНФ (СКНФ) функции по заданной таблице истинности.
2 Упрощение этой функции (преобразованию СДНФ (СКНФ) в формулу с
наименьшим числом вхождений переменных);
3. Построение соответствующей схемы.
41.
Образование СДНФ функции по заданной таблице истинности.Этот этап включает в себя следующие шаги:
1) в заданной таблице истинности выделяются наборы значений аргументов,
при которых функция принимает единичное значение;
2) для каждого выделенного набора образуется конституэнта единицы
(минтерм), принимающая единичное значение приданном наборе значений
аргументов;
3) составляется логическая сумма образованных конституэнт единицы.
Для образования конституэнты единицы Сi 1, принимающей единичное значение
при i-м наборе значений аргументов, необходимо составить логическое
произведение аргументов, в которое аргументы, принимающие в i-м наборе
единичное значение, входят без знака отрицания, а аргументы, принимающие в
i-м наборе нолевое значение, входят со знаком отрицания.
42.
При образовании совершенной конъюнктивной нормальной формы (СКНФ)функции:
1) в таблице выделяются наборы значений аргументов, при которых функция
принимает нолевое значение;
2) для каждого выделенного набора образуется конституэнта ноля,
принимавшая нолевое значение при данном наборе значений аргументов;
3) составляется логическое произведение образованных конституэнт ноля.
43.
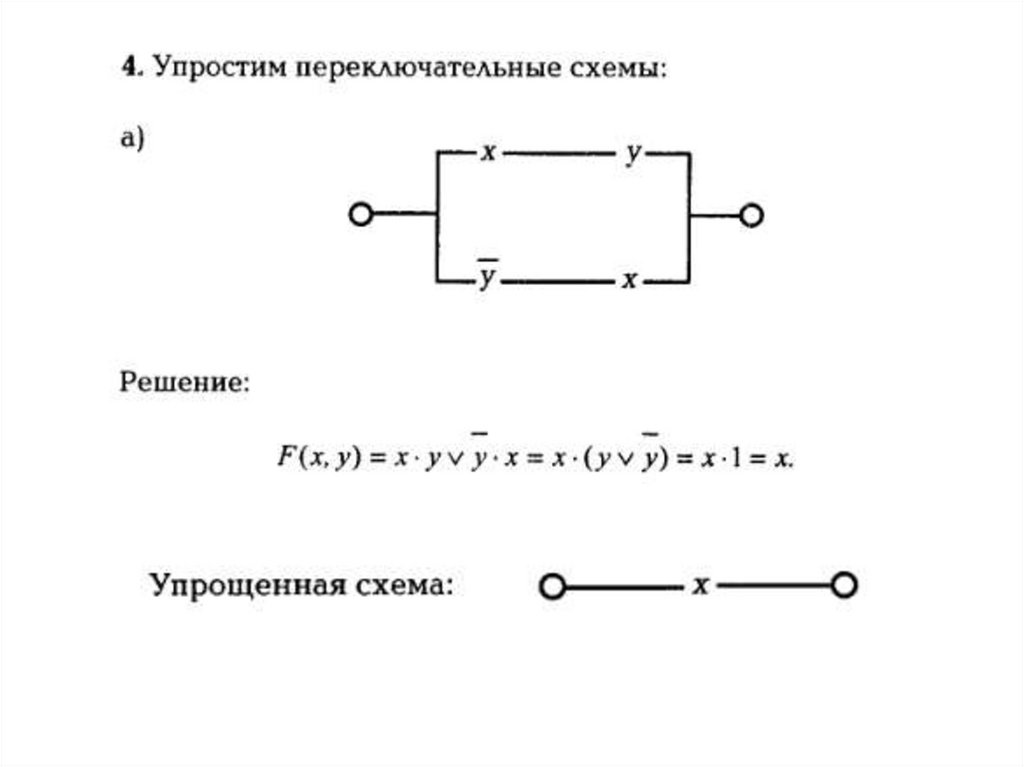
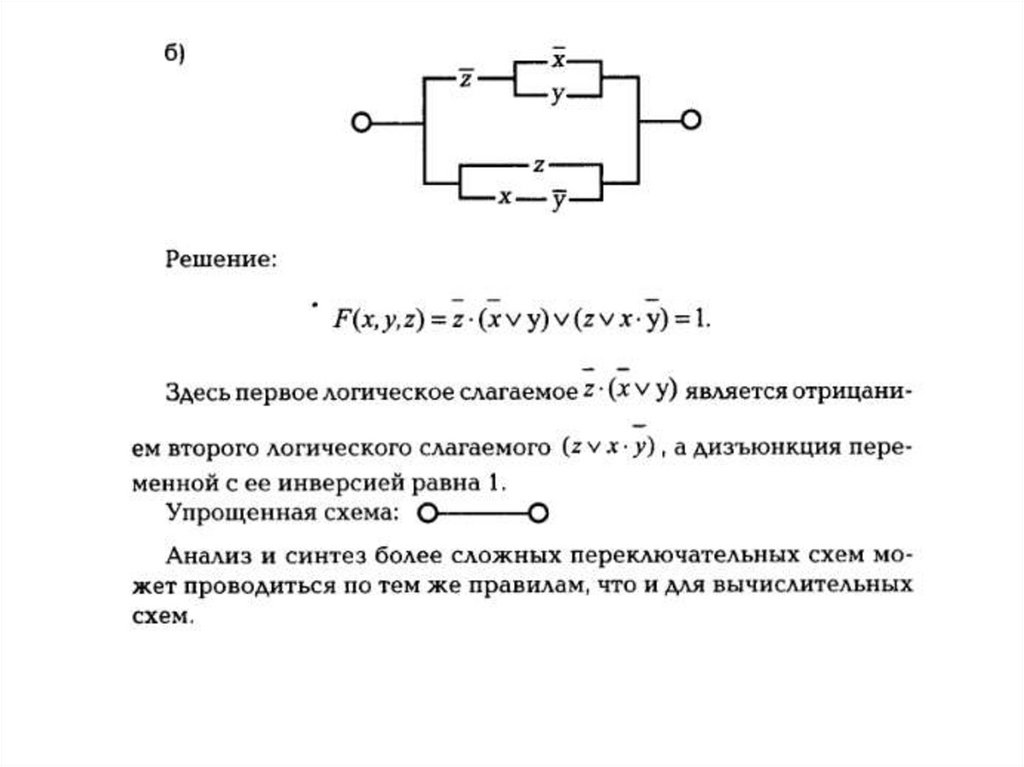
Упрощение функции.При преобразовании СДНФ (СКНФ) в формулу с наименьшим числом вхождений
переменных (минимизация формулы) используют следующие основные приемы:
1. вынос за скобки ХУ V XZ =_Х(У V Z);
2. полное склеивание ХУ V ХУ = X;
3. поглощение X V ХУ = X;
4. минимизация по методу Квайна;
5. минимизация с использованием карт Карно или диаграмм Вейча.
44.
Для карты Карно с помощью двух входов в таблицу, где указаны две части наборазначений аргументов, при котором соответствующая конституэнта единицы
принимает единичное значение. Карты Карно обычно используют для ручной
минимизации булевых функций при небольшом числе переменных (не более пяти)
На рис. представлены карты Карно для трех переменных. Каждая клетка
соответствует логическому произведению прямого или инверсного значения
переменных, присвоенных столбцу или строке, на пересечении которых она
находится.
В картах Карно значения переменных присваиваются таким образом, чтобы
соседние клетки по строкам и столбцам отличались между собой значением только
одной переменной, при этом обозначение значения логического произведения
переменных соответствует номеру клетки, записанному в коде Грея
45.
46.
47.
48.
Логический элемент — часть электронной логической схемы, которая реализуетэлементарную логическую функцию.











































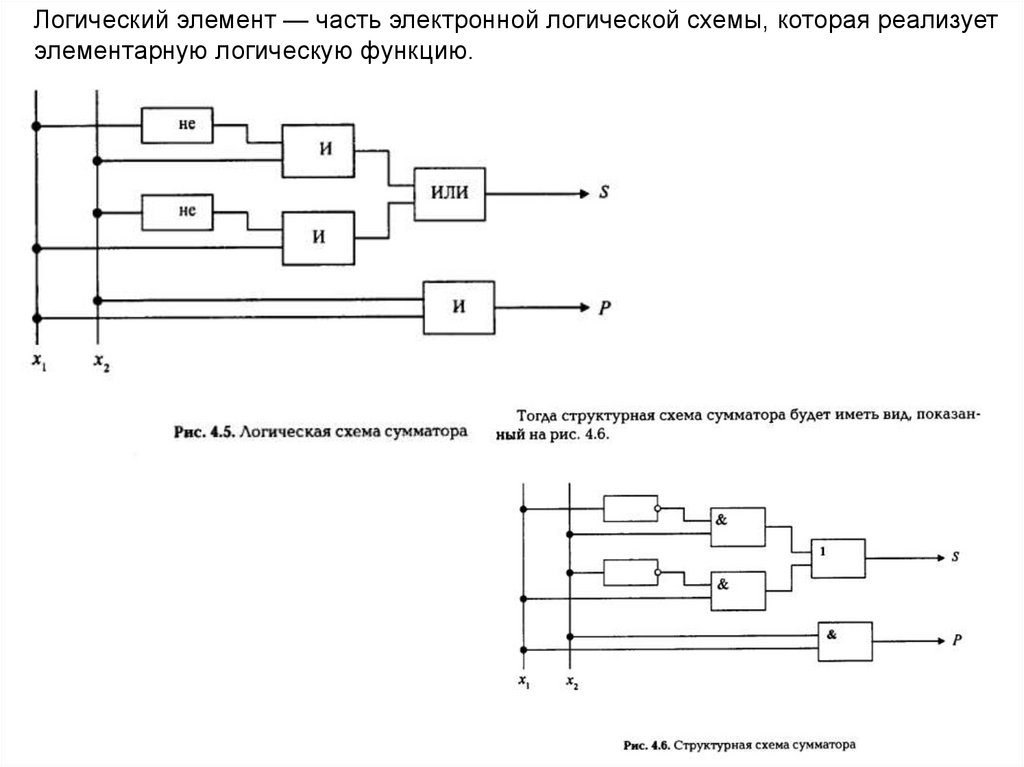
 Математика
Математика








