Подобные треугольники. Геометерия. 8 класс

1.

2.

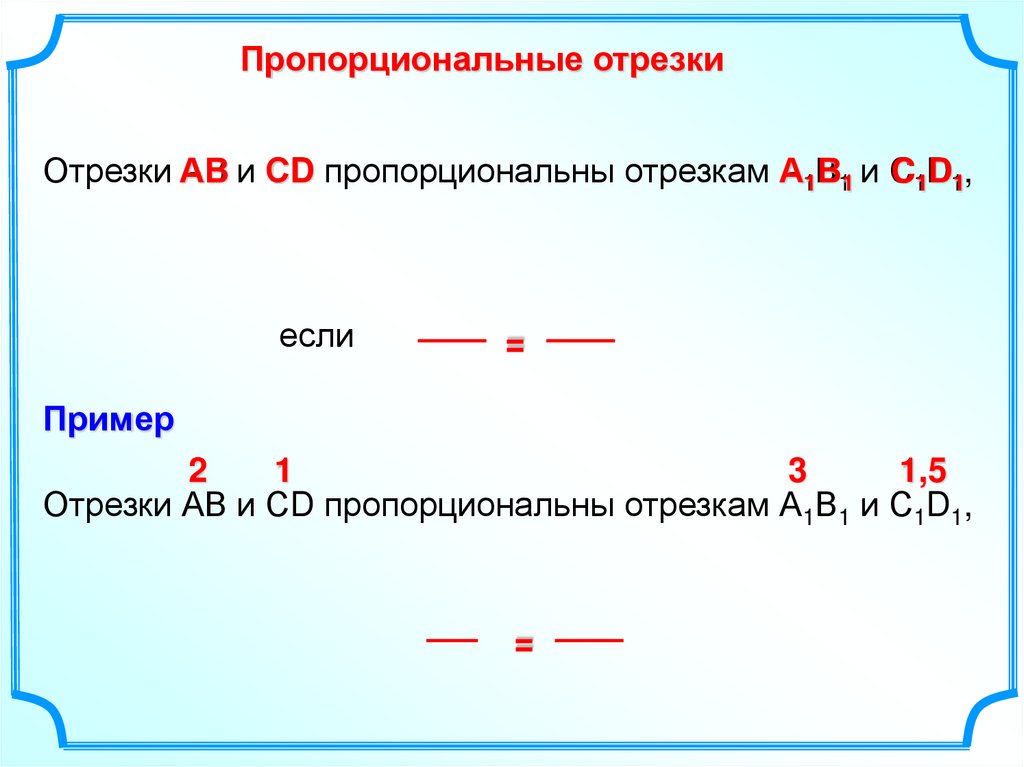
Пропорциональные отрезки
Отрезки АВ и СD пропорциональны отрезкам А1В11 и С
C1D1,
если
=
Пример
2
1
3
1,5
Отрезки АВ и СD пропорциональны отрезкам А1В1 и С1D1,
=

3.

Понятие пропорциональности вводится и для большего
числа отрезков.
Отрезки
АВ,
СD и EF пропорциональны отрезкам А1В11, С
АВ СD
C11D11 и E
E11FF11,
если
=
=

4.

В геометрии фигуры одинаковой формы принято
называть подобными.

5.

6.

Подобными являются любые два круга, два квадрата.

7.

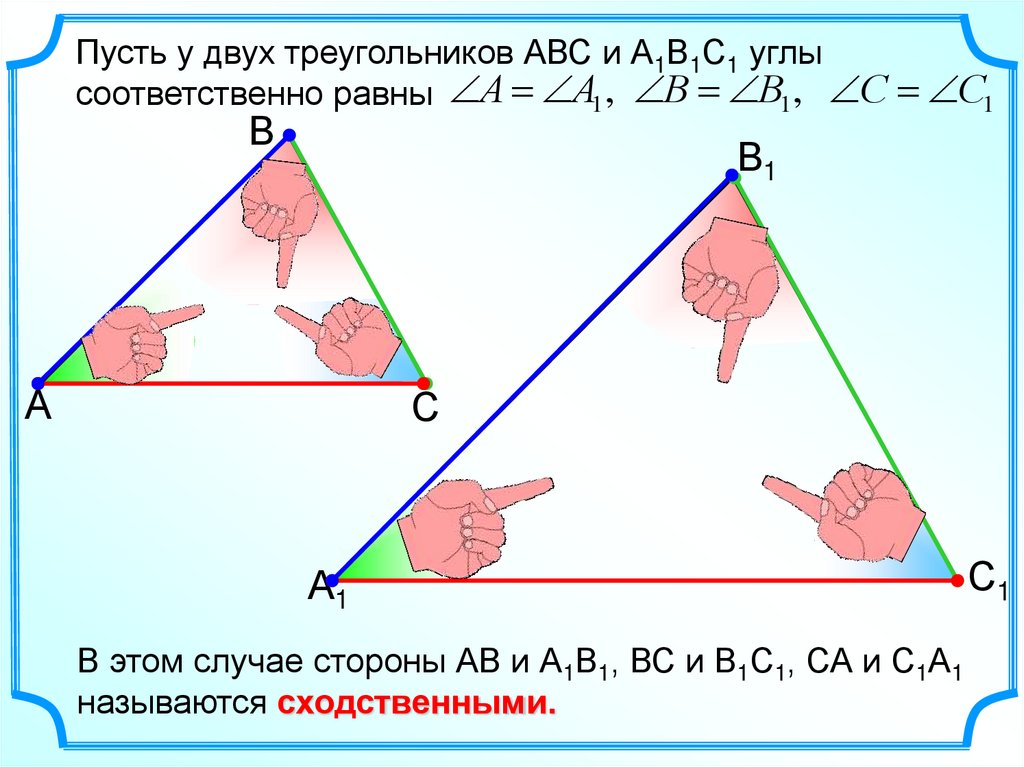
Пусть у двух треугольников АВС и А1В1С1 углы
соответственно равны А А1 , В В1 , С С1
В
В1
А
С
А1
В этом случае стороны АВ и А1В1, ВС и В1С1, СА и С1А1
называются сходственными.
С1

8.

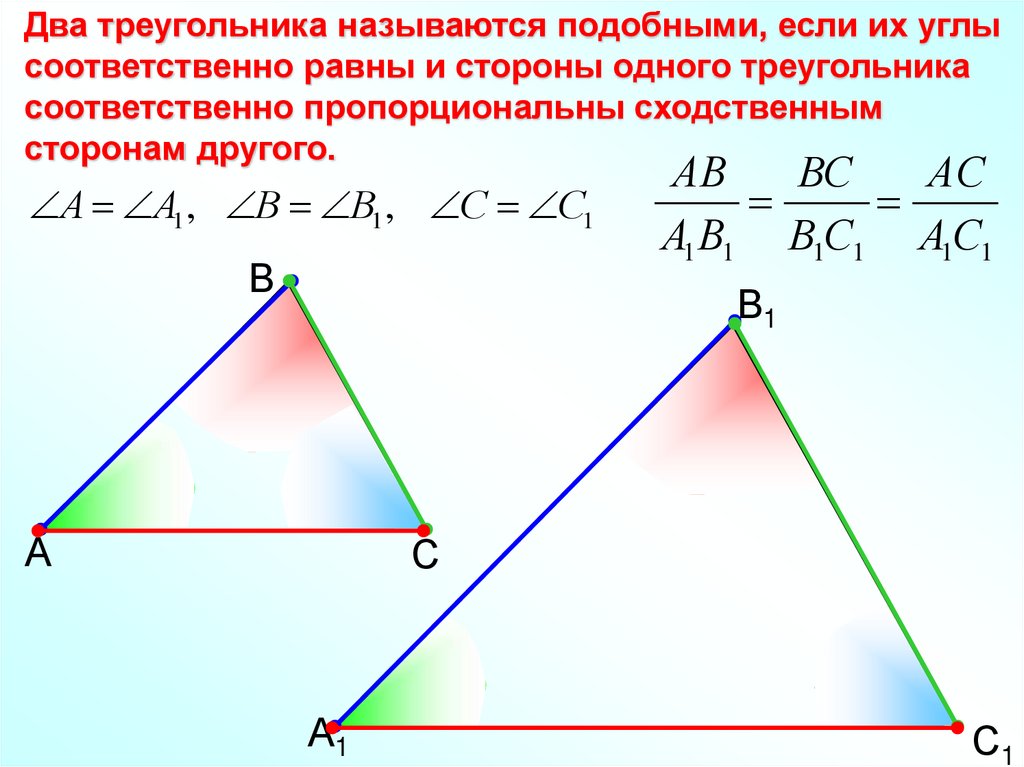
Два треугольника называются подобными, если их углы
соответственно равны и стороны одного треугольника
соответственно пропорциональны сходственным
сторонам другого.
А А1 , В В1 , С С1
В
АВ
ВС
АС
А1 В1 В1С1 А1С1
В1
А
С
А1
С1

9.

Число k, равное отношению сходственных сторон
подобных треугольников, называется коэффициентом
подобия.
АВ
ВС
АС
=
k
А1 В1 В1С1 А1С1
ABC
A1B1C1
В1
В
А
С
А1
С1

10.

№ 541
Доказать: ABC
А Е
22,8
F
B D
C F
D
400
А
340
13,2
1060
4,4
400
С
EFD
5,2
1060
340
7,6
15,6
E
В
5,2
7 ,6
4,4
Верно
13,2 15,6 22,8

11.

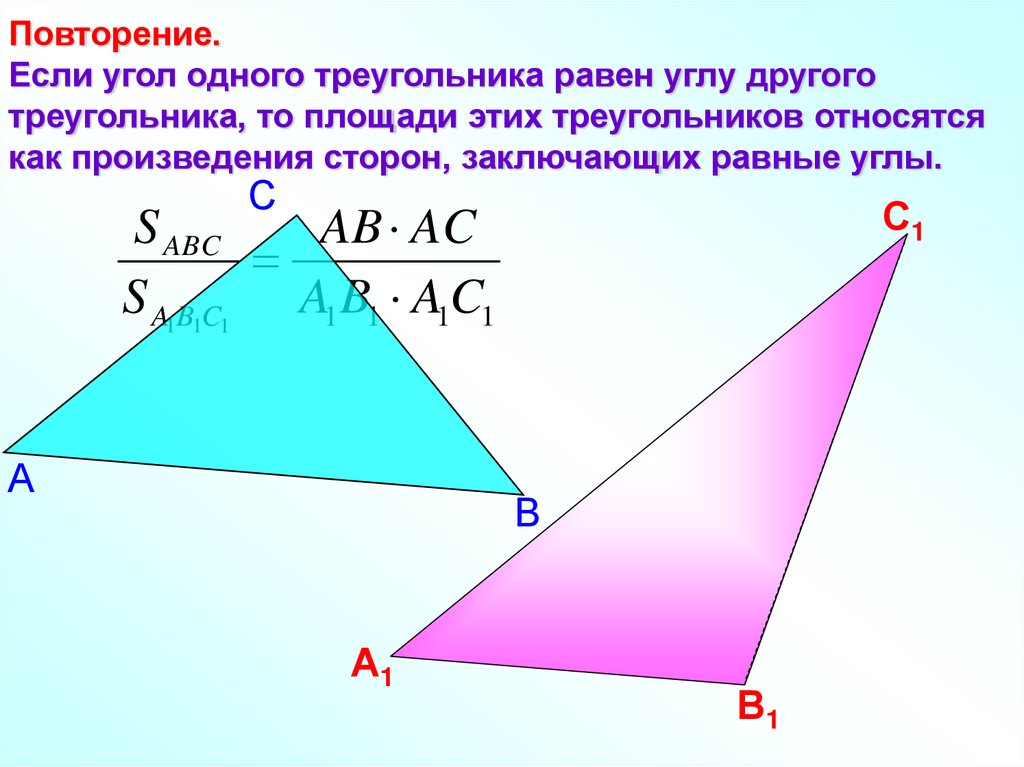
Повторение.
Если угол одного треугольника равен углу другого
треугольника, то площади этих треугольников относятся
как произведения сторон, заключающих равные углы.
С
S ABC
AB AC
S A1B1C1 A1 B1 A1C1
А
С1
В
А1
В1

12.

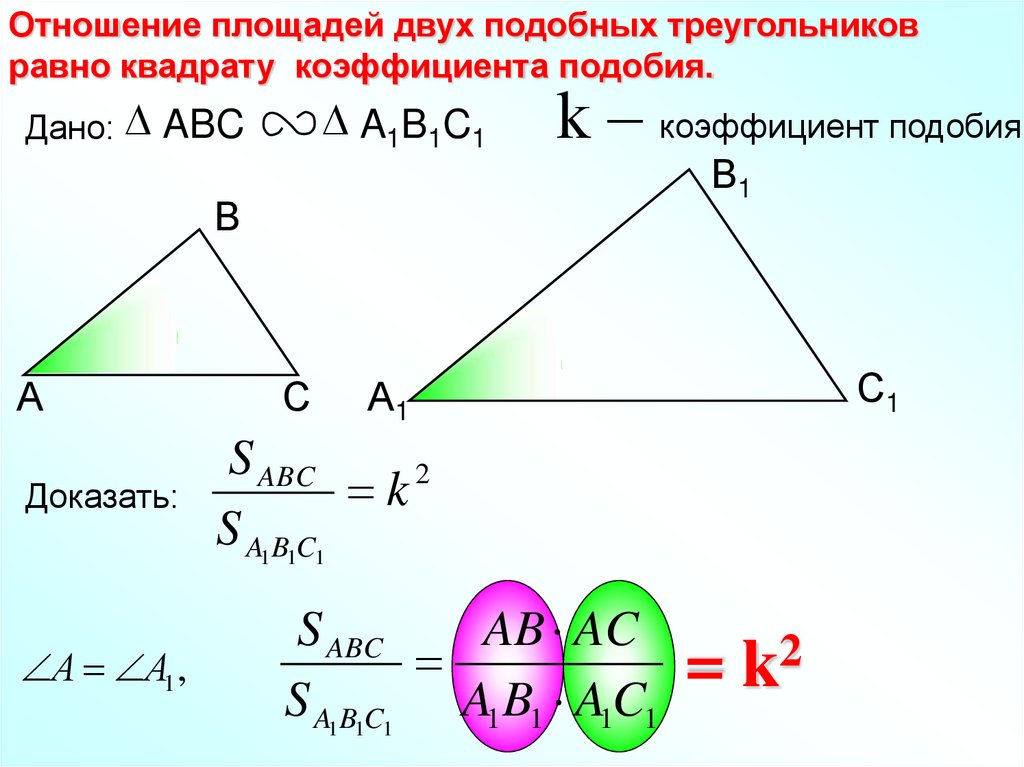
Отношение площадей двух подобных треугольников
равно квадрату коэффициента подобия.
Дано: ABC
A1B1C1
В
А
Доказать:
А А1 ,
С
k – коэффициент подобия
В1
А1
S ABC
2
k
S A1B1C1
S ABC
AB AC
2
=
k
S A1B1C1 A1 B1 A1C1
С1

13.

№547.
A1B1C1
Дано: ABC
Отношение периметров двух
коэффициент подобия
подобных треугольников
равно коэффициенту подобия.
РABC
k
Доказать:
k–
АВ
k
А1 В1
АС
k
А1С1
ВС
k
В1С1
АВ k А1В1
+
РA1B1C1
АС k А1С1
РАВС k А1В1 k A1C1 k B1C1
РАВС k ( А1В1 A1C1 B1C1 )
ВС k В1С1
РАВС k РА1В1С1 : Р А1В1С1
РABC
k
РA1B1C1

14.

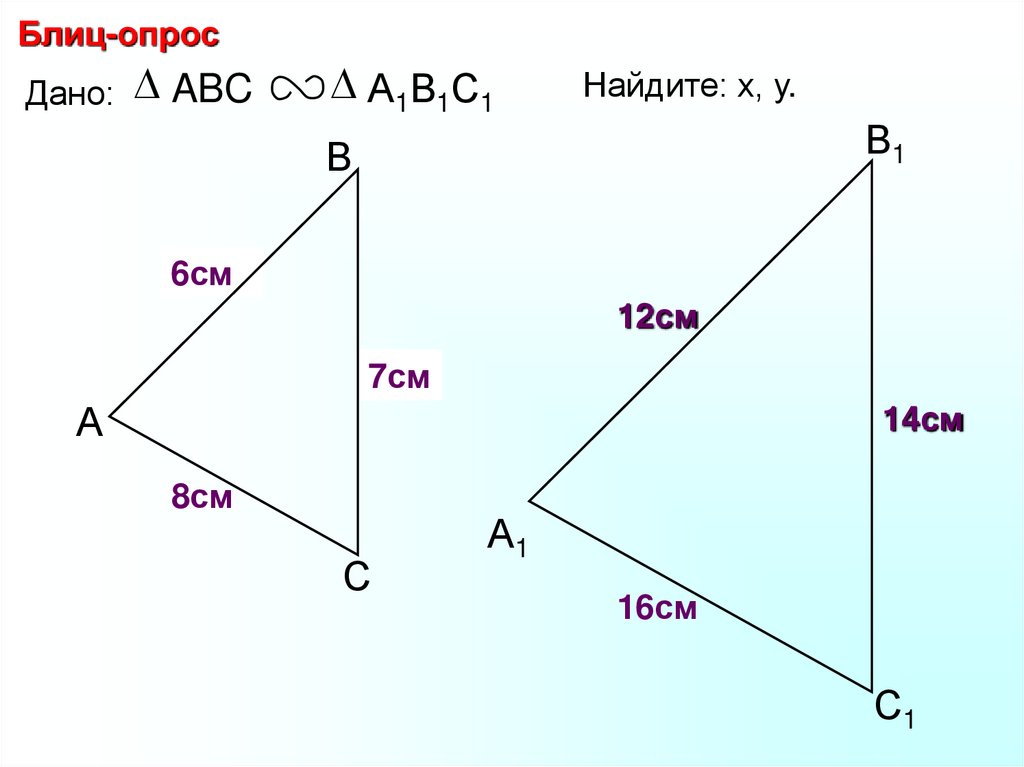
Блиц-опрос
Дано: ABC
А1В1С1
Найдите: х, у, z.
А1 В1
2
АВ
В
В1
7см
6см
12см
х
А
8см
14см
у
С
А1
16см
z
С1

15.

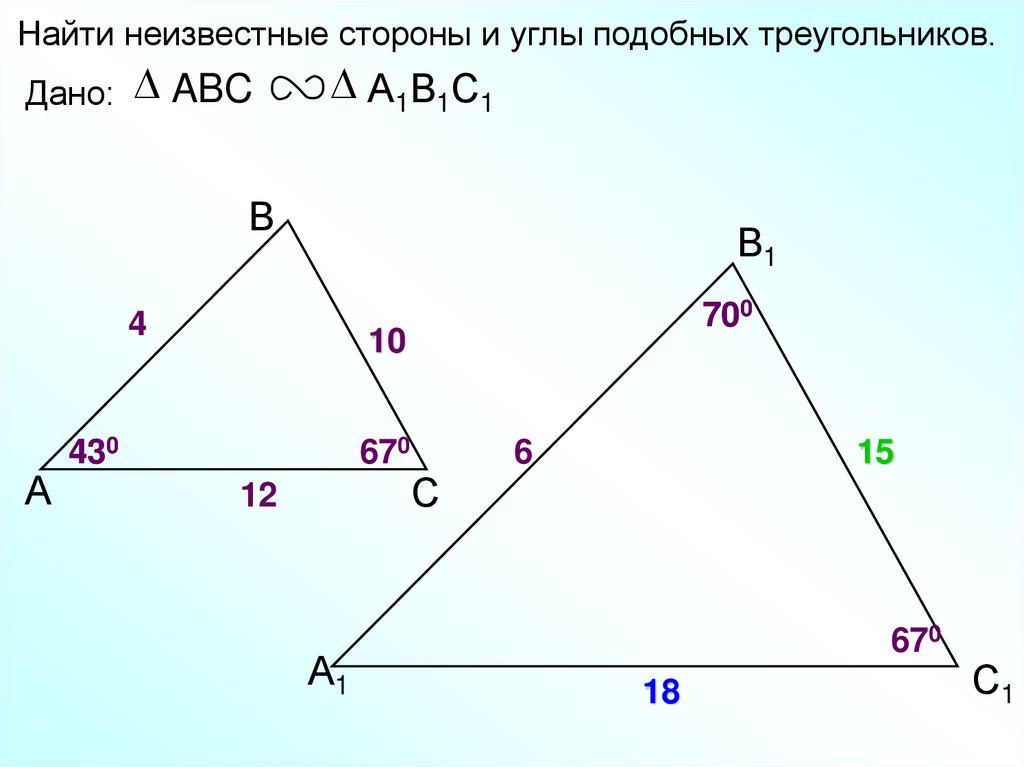
Найти неизвестные стороны и углы подобных треугольников.
Дано: ABC
А1В1С1
В
В1
4
А
700
10
430
670
12
А1
С
6
15
670
18
С1

16.

Блиц-опрос
Дано: ABC
А1В1С1
Найдите: х, у, z.
А1 В1
2
АВ
В
В1
10,5см
у
9смх
18см
А
12см
z
21см
С
А1
24см
С1

17.

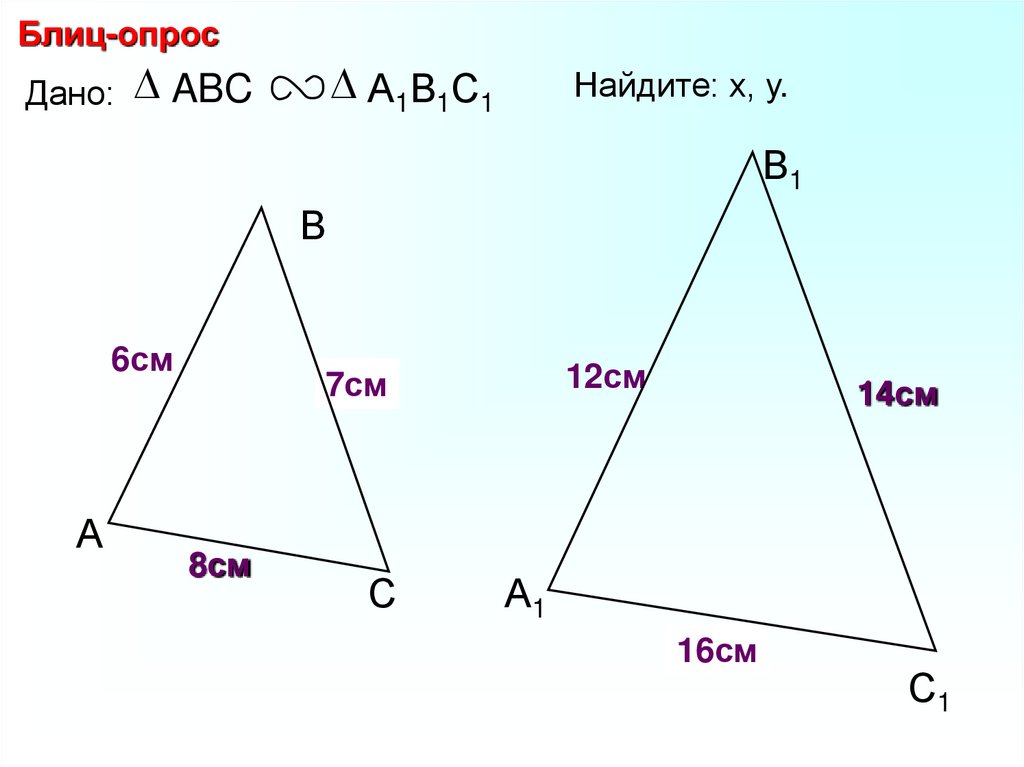
Блиц-опрос
Дано: ABC
А1В1С1
В
Найдите: х, у.
В1
6см
7см
21см
х
18см
А
8см
С
А1
у
24см
С1

18.

Блиц-опрос
Дано: ABC
А1В1С1
Найдите: х, у.
В1
В
6см
х
12см
7см
у
А
14см
8см
С
А1
16см
С1

19.

Блиц-опрос
Дано: ABC
А1В1С1
Найдите: х, у.
В1
В
6см
А
х
7см
8см
С
12см
А1
14см
у
16см
С1

20.

Блиц-опрос
Дано: ABC
А1В1С1
Р А1В1С1 105см
Найдите: х, у,z.
В
В1
6см
7см
РАВС 21см
А
8см
РA1B1C1
РABC
5
35см
y
х
30см
С
А1
z
40см
С1

21.

Дано: ABC
ORV
C V
Найти все углы треугольников
A O
B R
В
O
V
800
А
310
АВ
ВС
АС
OR
OV
RV
310
690
69
С
800
R

22.

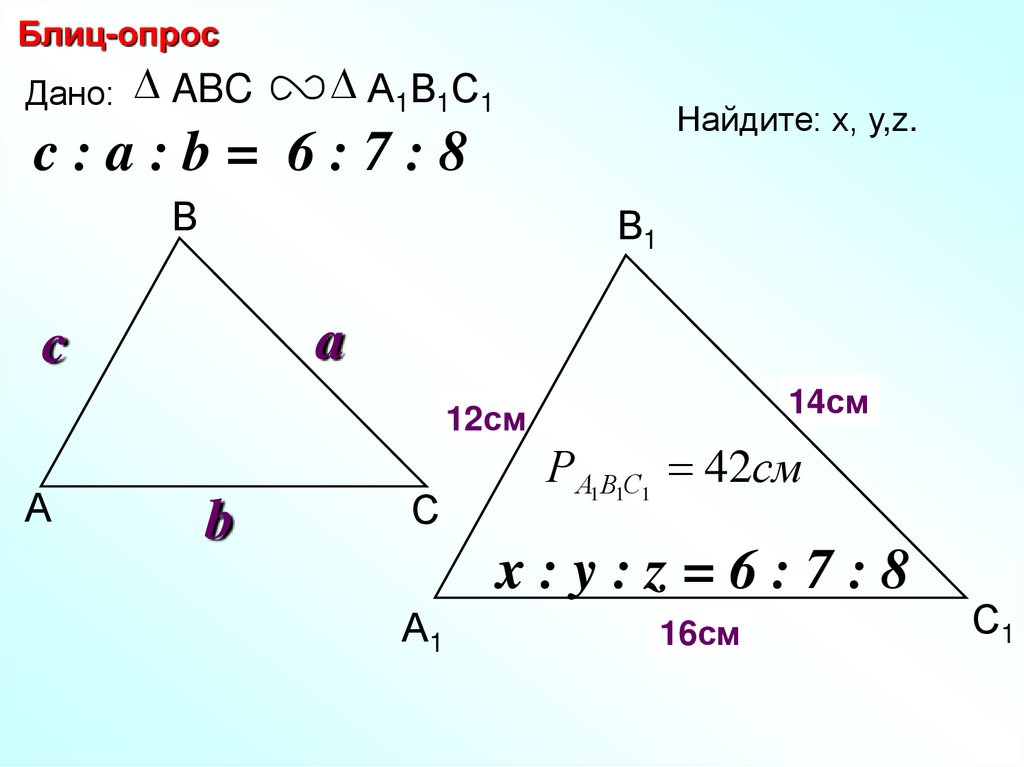
Блиц-опрос
Дано: ABC
А1В1С1
Найдите: х, у,z.
c:a:b= 6:7:8
В
В1
a
c
х
12см
А
b
С
14см
y
РА1В1С1 42см
x:y:z=6:7:8
А1
z
16см
С1

23.

Блиц-опрос
Дано: ABC
А1В1С1
Найдите: х, у.
c:a:b= 6:7:8
В
В1
a
c
12см
х
А
b
14см
y
С
x:y:z=6:7:8
А1
16см
С1

24.

Блиц-опрос
Дано: ABC
А1В1С1
y – x = 4 см
c:a:b= 6:7:8
В
Найдите: х, у.
В1
a
c
24см
х
А
b
y
28см
С
x:y:z=6:7:8
А1
z
32см
С1

25.

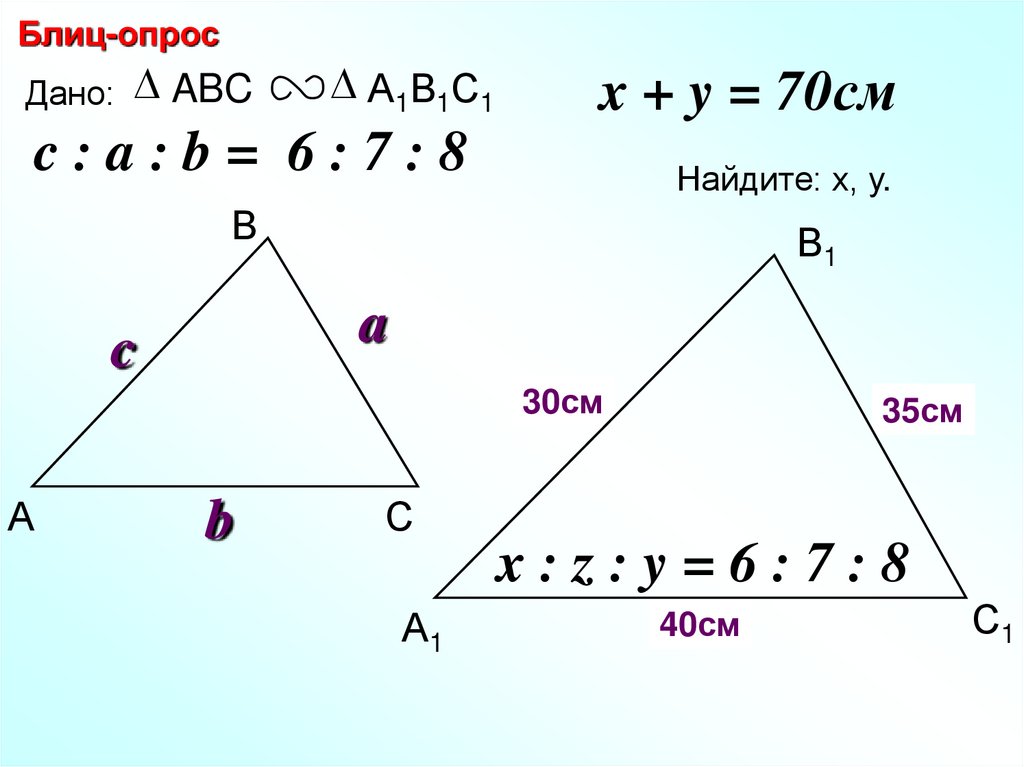
Блиц-опрос
Дано: ABC
А1В1С1
x + y = 70см
c:a:b= 6:7:8
Найдите: х, у.
В
В1
a
c
30см
х
А
b
35см
Z
С
x:z:y=6:7:8
А1
40см
y
С1