Инженерная геодезия. Лекция 3

1.

ИНЖЕНЕРНАЯ ГЕОДЕЗИЯ
Лектор:
Хремли Галина Павловна,
cтарший преподаватель
Lecturer:
Khremli Galina
Лекция 3

2.

Системы координат в геодезии
Основные понятия при определении координат точек местности
Для определения положения точек местности используется референц-эллипсоид,
в каждой точке которого существует два основных направления: направление
нормали к поверхности и направление линии силы тяжести.
Координаты,
определяемые
геодезическими.
с
использованием
нормали,
называют
Координаты, определяемые с использованием линии направления силы
тяжести, называют астрономическими.
Существует два вида меридианов: геодезический и астрономический.
Геодезический меридиан определяется линией пересечения с поверхностью
Земли плоскости, которая проходит через нормаль к поверхности референцэллипсоида и через ось вращения Земли.
Астрономический меридиан определяется линией пересечения с
поверхностью Земли плоскости, проходящей через отвесную линию в данной
точке параллельно оси вращения Земли.
Лекция 3. Системы координат в геодезии
Lecture 3.
2

3.

Системы координат в геодезии
Основные понятия при определении координат точек местности
Меридиан – линия пересечения с поверхностью
параллельной оси вращения либо проходящей через нее.
Земли
плоскости,
Параллель – линия пересечения
перпендикулярной к оси вращения.
Земли
плоскости,
с
поверхностью
Гринвичский меридиан (начальный, нулевой меридиан) – это меридиан,
проходящий через установленную точку в Гринвичской обсерватории (Англия).
В России существует аналогичный Пулковский меридиан, координаты
которого определяются в системе координат Гринвичского меридиана.
Координатами называются угловые или линейные величины, определяющие
положение точек на плоскости или в пространстве относительно направлений и
плоскостей, выбранных в качестве исходных в данной системе координат.
Для определения положения точек в геодезии применяют:
пространственные прямоугольные координаты,
геодезические координаты,
плоские прямоугольные координаты.
Лекция 3. Системы координат в геодезии
Lecture 3.
3

4.

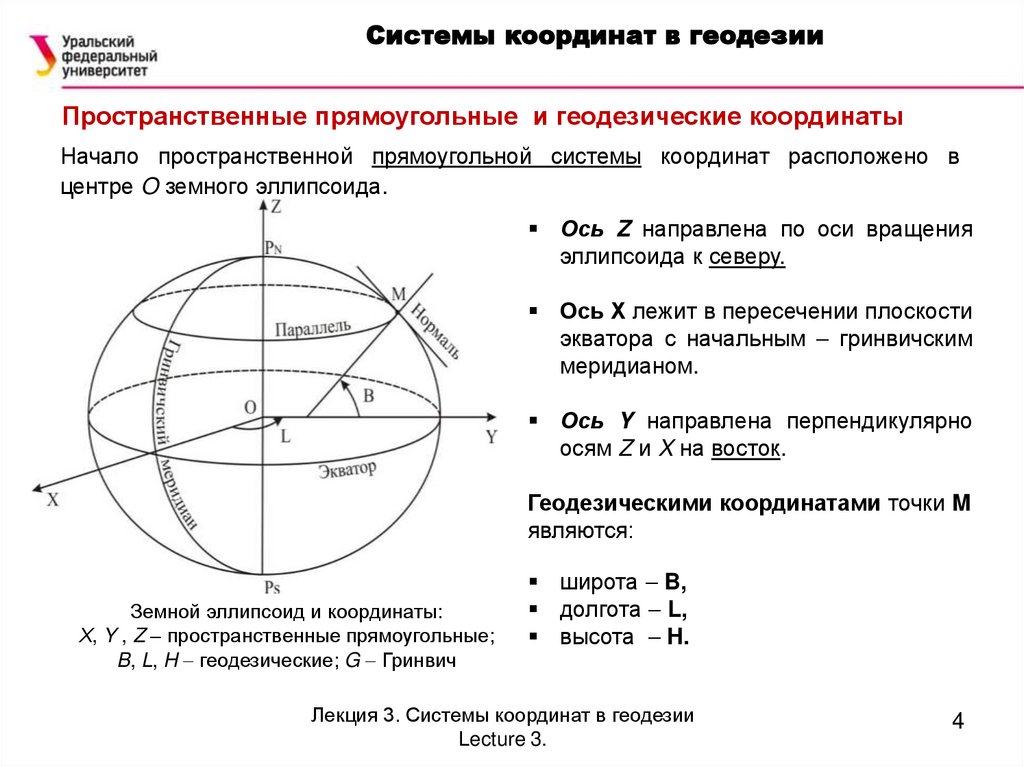
Системы координат в геодезии
Пространственные прямоугольные и геодезические координаты
Начало пространственной прямоугольной системы координат расположено в
центре O земного эллипсоида.
Ось Z направлена по оси вращения
эллипсоида к северу.
Ось Х лежит в пересечении плоскости
экватора с начальным гринвичским
меридианом.
Ось Y направлена перпендикулярно
осям Z и X на восток.
Геодезическими координатами точки M
являются:
Земной эллипсоид и координаты:
Х, Y , Z – пространственные прямоугольные;
B, L, H геодезические; G Гринвич
широта B,
долгота L,
высота H.
Лекция 3. Системы координат в геодезии
Lecture 3.
4

5.

Системы координат в геодезии
Геодезические координаты
Геодезической широтой точки М называется угол В, образованный
нормалью к поверхности эллипсоида, проходящей через точку, и плоскостью
экватора. Широта отсчитывается от экватора к северу и югу от 0 до 90 и
называется северной (положительной) или южной (отрицательной).
Геодезической долготой точки М называется двугранный угол L, между
плоскостями начального геодезического меридиана и геодезического
меридиана точки. Долготы отсчитывают от начального меридиана от 0 до 360
на восток, или от 0 до 180 на восток (положительные) и от 0 до 180 на запад
(отрицательные).
Геодезической высотой точки М является ее высота Н над поверхностью
земного эллипсоида.
Пусть
e
первый
эксцентриситет
меридианного эллипса, N радиус кривизны
первого вертикала (N=a/(1 e2 sin2B)1/2).
Тогда,
геодезические
координаты
с
пространственными
прямоугольными
координатами связаны формулами:
X = (N + H) cosB cosL,
Y = (N + H) cosB sinL,
Z = [(1 e2) N+H] sinB.
Лекция 3. Системы координат в геодезии
Lecture 3.
5

6.

Системы координат в геодезии
Астрономические координаты
Астрономические координаты отличаются от геодезических на величину угла между
направлением нормали к поверхности эллипсоида и отвесной линией в данной
точке земной поверхности, который называется уклонением отвесной линии.
Астрономическая широта
угол, составленный отвесной линией
в данной точке с
плоскостью
экватора.
Астрономические координаты
Астрономическая долгота –
угол
между
плоскостями
Гринвичского
меридиана
и
проходящего через отвесную линию в
данной
точке
астрономического
меридиана.
Лекция 3. Системы координат в геодезии
Lecture 3.
6

7.

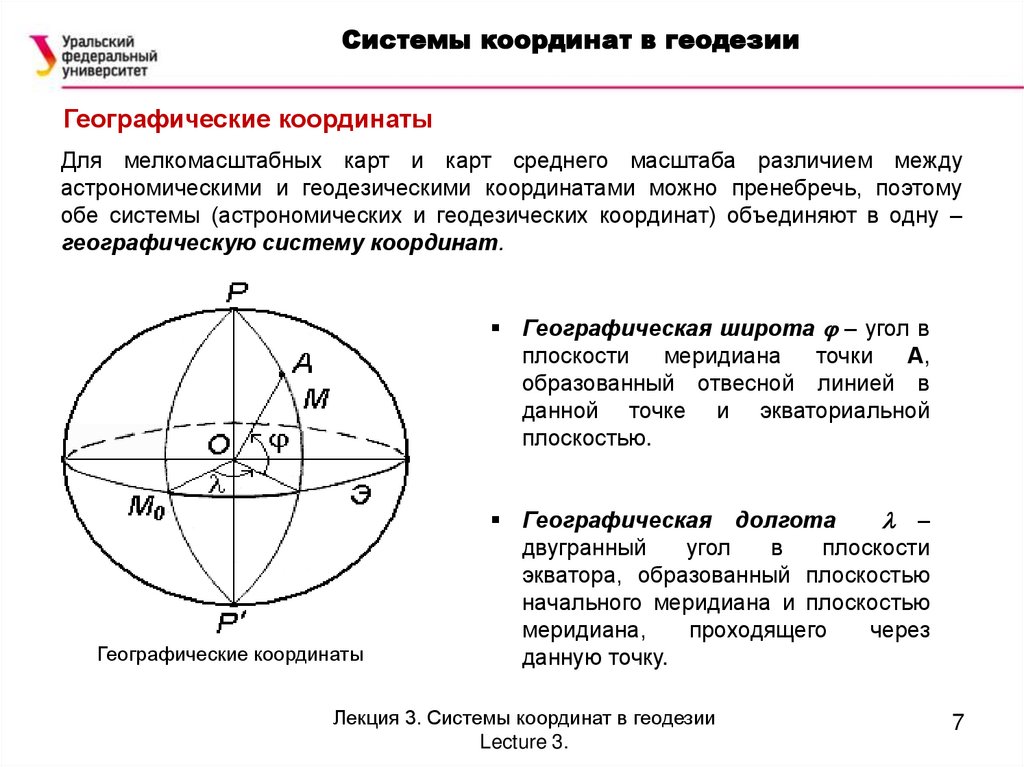
Системы координат в геодезии
Географические координаты
Для мелкомасштабных карт и карт среднего масштаба различием между
астрономическими и геодезическими координатами можно пренебречь, поэтому
обе системы (астрономических и геодезических координат) объединяют в одну –
географическую систему координат.
Географическая широта – угол в
плоскости меридиана
точки
А,
образованный отвесной линией в
данной точке и экваториальной
плоскостью.
Географические координаты
Географическая долгота
–
двугранный
угол
в
плоскости
экватора, образованный плоскостью
начального меридиана и плоскостью
меридиана,
проходящего
через
данную точку.
Лекция 3. Системы координат в геодезии
Lecture 3.
7

8.

Системы координат в геодезии
Геодезические и географические системы координаты (повторение)
Геодезическую систему координат характеризуют координаты: B, L, H.
Географическую систему координат характеризуют координаты: , , Н.
а) Геодезическая система координат
б) Географическая система координат
Лекция 3. Системы координат в геодезии
Lecture 3.
8

9.

Системы координат в геодезии
Плоские прямоугольные координаты
Для решения задач инженерной геодезии от пространственных и геодезических
координат переходят к более простым – плоским прямоугольным координатам.
Положение точки в прямоугольной системе
однозначно
определяется
двумя
координатами X и Y: координата X выражает
расстояние точки от оси ОY, координата Y –
расстояние от оси OХ.
Координатные оси делят плоскость на
четыре четверти, которые нумеруются. Счет
идет по ходу стрелки от положительного
направления оси абсцисс .
Положение точек в системе
плоских прямоугольных координат
Значения координат бывают положительные
и отрицательные в зависимости от того, в
какой четверти находится искомая точка.
Лекция 3. Системы координат в геодезии
Lecture 3.
9

10.

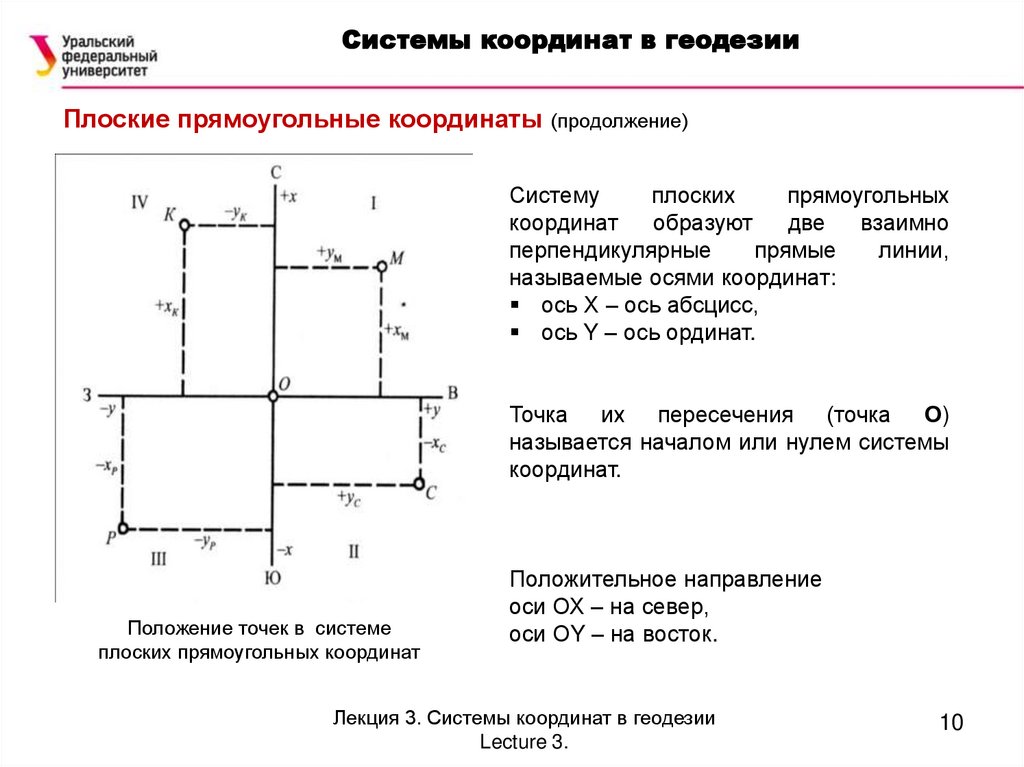
Системы координат в геодезии
Плоские прямоугольные координаты (продолжение)
Систему
плоских
прямоугольных
координат
образуют
две
взаимно
перпендикулярные
прямые
линии,
называемые осями координат:
ось Х – ось абсцисс,
ось Y – ось ординат.
Точка их пересечения (точка О)
называется началом или нулем системы
координат.
Положение точек в системе
плоских прямоугольных координат
Положительное направление
оси ОХ – на север,
оси ОY – на восток.
Лекция 3. Системы координат в геодезии
Lecture 3.
10

11.

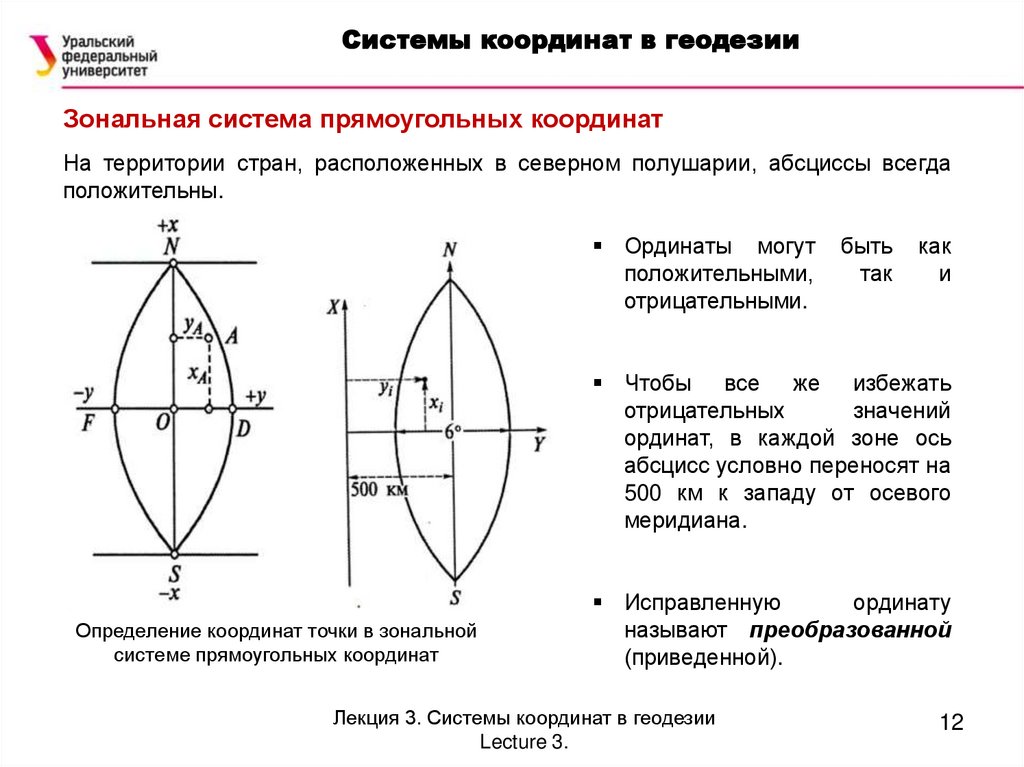
Системы координат в геодезии
Зональная система прямоугольных координат
Зональная система плоских прямоугольных
координат
находит
применение
при
составлении и обновлении планов и карт.
Каждая
шестиградусная
зона
имеет
прямоугольную систему координат со своим
началом координат – точкой пересечения
экватора с осевым меридианом зоны.
Осевой меридиан зоны изображается прямой
линией и принимается за ось абсцисс (х); осью
ординат (y) является изображение экватора.
Отдельная зона Гаусса-Крюгера
Остальные меридианы и параллели в пределах
зоны изобразятся кривыми линиями (дугами)
Лекция 3. Системы координат в геодезии
Lecture 3.
11

12.

Системы координат в геодезии
Зональная система прямоугольных координат
На территории стран, расположенных в северном полушарии, абсциссы всегда
положительны.
Ординаты могут
положительными,
отрицательными.
быть
так
как
и
Чтобы все же избежать
отрицательных
значений
ординат, в каждой зоне ось
абсцисс условно переносят на
500 км к западу от осевого
меридиана.
Определение координат точки в зональной
системе прямоугольных координат
Исправленную
ординату
называют преобразованной
(приведенной).
Лекция 3. Системы координат в геодезии
Lecture 3.
12

13.

Системы координат в геодезии
Зональная система прямоугольных координат (продолжение)
В каждой из шестидесяти зон
численные значения координат х и у
могут повторяться.
Поэтому
для
однозначного
определения положения точки на
земной поверхности перед каждой
ординатой ставится номер зоны.
Определение координат точки в зональной
системе прямоугольных координат
Например, пусть точка В находится в
11 зоне, ее ордината уВ = 666,515 км.
Тогда ее полная преобразованная
ордината будет равна: уВ = 11666,515
км.
Лекция 3. Системы координат в геодезии
Lecture 3.
13

14.

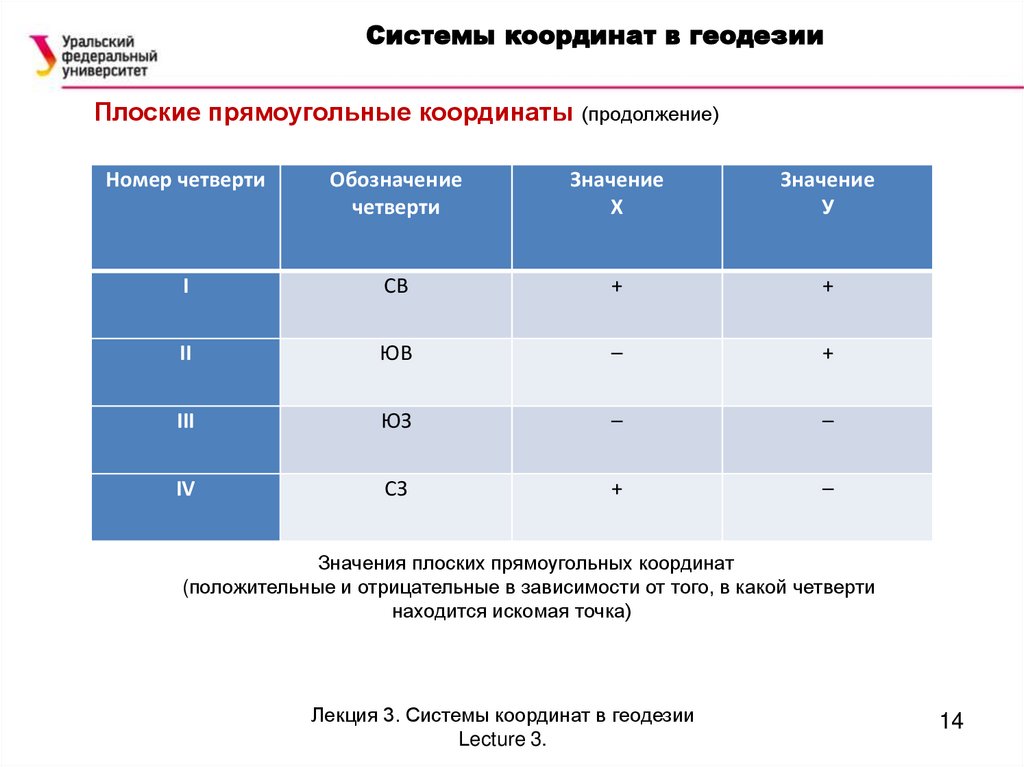
Системы координат в геодезии
Плоские прямоугольные координаты (продолжение)
Номер четверти
Обозначение
четверти
Значение
Х
Значение
У
I
СВ
+
+
II
ЮВ
–
+
III
ЮЗ
–
–
IV
СЗ
+
–
Значения плоских прямоугольных координат
(положительные и отрицательные в зависимости от того, в какой четверти
находится искомая точка)
Лекция 3. Системы координат в геодезии
Lecture 3.
14

15.

Системы координат в геодезии
Плоские полярные системы координат
При выполнении съемочных и разбивочных геодезических работ применяют
полярную систему координат. Она состоит из полюса системы О и полярной оси
ОХ, в качестве которых принимается прямая с известным началом и направлением.
Для определения положения точек в данной
системе
используют
линейно-угловые
координаты:
полярный угол β, отсчитываемый по
часовой стрелке от полярной оси ОР до
направления на горизонтальную проекцию
точки А’,
полярное расстояние r от полюса системы
О до проекции А’, которое называется
радиусом-вектором r.
Плоская полярная система координат
Лекция 3. Системы координат в геодезии
Lecture 3.
15

16.

Системы координат в геодезии
Плоские полярные системы координат (продолжение)
Полярный угол β отсчитывается от оси OX по ходу часовой стрелки.
Положение полярной оси выбирают произвольно или совмещают ее с
направлением истинного меридиана.
Рассмотрим переход от прямоугольных
координат к полярным и обратно для
случая, когда начала обеих систем
находятся в одной точке и оси OX у
них совпадают.
Из ΔOBA:
X = S сos β,
Y = S sin β,
tg β = Y / X,
Переход от прямоугольных координат
к полярным
S = Х2 +