Метод Монте - Карло

1.

Метод Монте - Карло
"Люди - як гральні кості: ми
кидаємо себе вперед по
життю.“
Жан-Поль Сартр
1

2.

2

3.

• Ме́тод Мо́нте-Ка́рло (за назвою міста МонтеКарло, Монако, яке відоме своїми казино) —
загальна назва групи числових методів,
заснованих на одержанні великої кількості
реалізацій стохастичного (випадкового)
процесу, який формується у той спосіб, щоб
його ймовірнісні характеристики збігалися з
аналогічними величинами задачі, яку
потрібно розв'язати. Використовується для
розв'язування задач у фізиці, математиці,
економіці, оптимізації, теорії управління
тощо.
3

4.

4

5.

• Метод Монте-Карло — це метод імітації для
приблизного відтворення реальних явищ. Він
об'єднує аналіз чутливості (сприйнятливості) і
аналіз розподілу ймовірностей вхідних змінних.
Цей метод дає змогу побудувати модель,
мінімізуючи дані, а також максимізувати значення
даних, які використовуються в моделі.
Побудова моделі починається з визначення
функціональних залежностей у реальній системі.
Після чого можна одержати кількісний розв'язок,
використовуючи теорію ймовірності й таблиці
випадкових чисел.
• Метод Монте-Карло широко використовується 5у
всіх випадках симуляції на ЕОМ.

6.

Метод Монте-Карло (багаторазове імітаційне
моделювання ймовірностей) є математичним
методом, за допомогою якого можна оцінити можливі
результати невизначеної події
На відміну від звичайної моделі прогнозування
метод Монте-Карло створює модель можливих
результатів з використанням розподілу ймовірностей
У типовому експерименті Монте-Карло дана
операція повторюється кілька тисяч разів для
створення великої кількості можливих результатів.
Крім того, висока точність методу Монте-Карло
дозволяє використовувати його для довгострокового
прогнозування.
6

7. Метод Монте-Карло застосовується для апроксимації значення π. Після розміщення 30000 випадкових точок, оцінка для π знаходиться

Метод Монте-Карло застосовується для апроксимації значення π. Після розміщення
30000 випадкових точок, оцінка для π знаходиться в межах 0,07 % від фактичного
значення.
7

8.

• Ме́тод Мо́нте-Ка́рло — загальна назва
групи числових методів, заснованих на
одержанні великої кількості реалізацій
стохастичного (випадкового) процесу,
який формується у той спосіб, щоб його
ймовірнісні характеристики збігалися з
аналогічними величинами задачі, яку
потрібно розв'язати.
8

9. Історична довідка

• Перед тим як метод Монте-Карло був
розроблений, тестування випробуванням
раніше розумілося як детермінована
задача, і статистична вибірка була
використана для оцінки невизначеностей
в моделюванні. Моделювання за методом
Монте-Карло змінило цей підхід до
вирішення задач з використанням
детермінованих ймовірнісних аналогів
9

10. Історична довідка

Енріко Фермі в 1930-х і Станіславу Уламу в 1946 році прийшла в голову
ідея подібного методу. Улам пізніше зв'язався з Джоном фон Нейманом,
щоб працювати над ним.
Фізики з Лос-Аламоської наукової лабораторії досліджували радіаційний
захист та відстань, яку нейтрони проходять через різні матеріали. Зважаючи
на велику кількість необхідних даних, таких як середня відстань, яку
нейтрони проходять в речовині до зіткнення з атомним ядром або скільки
енергії нейтрони мають віддати, щоб зіткнутися з ядром, задача не могла
бути розв'язана за допомогою аналітичних розрахунків.
Джон фон Нейман і Станіслав Улам запропонували розв'язати її на основі
моделювання експерименту на комп'ютері за допомогою випадку. Будучи
засекреченою, їхня робота потребувала кодової назви. Фон Нейман вибрав
назву «Монте-Карло». Назва запозичена від казино Монте-Карло в Монако,
для гри в якому дядько Улама позичав гроші.
Над методом Монте-Карло працював також Ніколас Костянтин Метрополіс.
10

11.

Моделювання за методом Монте-Карло
використовується для моделювання
ймовірності різних результатів у процесі, який
неможливо легко передбачити через
втручання випадкових змінних. Це техніка,
яка використовується для розуміння впливу
ризику та невизначеності.
11

12. Метод Монте-Карло

• Не існує єдиного методу Монте-Карло, цей термін
описує великий і широко використовуваний клас
підходів. Проте ці підходи використовують в своїй
основі єдиний шаблон:
• Визначити область можливих вхідних даних.
• Випадковим чином згенерувати вхідні дані із
визначеної вище області за допомогою деякого
заданого розподілу ймовірностей.
• Виконати детерміновані обчислення над вхідними
даними.
• Проміжні результати окремих розрахунків звести у
кінцевий результат.
12

13. Метод Монте-Карло

• Савіловський[en] перерахував характеристики високоякісного
моделювання методом Монте-Карло:
• (Псевдо-випадковий) генератор чисел має певні характеристики
(наприклад, довгий «період» до того, як послідовність
повторюється)
• (Псевдо-випадковий) генератор чисел генерує значення, які
проходять випробування на випадковість
• є достатня кількість зразків для забезпечення точних
результатів
• використовується належний метод вибірки
• алгоритм, який використовується, є дієвим для ситуації, що
моделюється
• він імітує явища.
13

14.

• Fundamentals of the Monte Carlo method
for neutral and charged particle transport
Alex F Bielajew – 2000.
• «Метод Монте-Карло передує
комп’ютеру (докладніше про це пізніше)
і не є суттєвим для виконання рішення,
хоча в більшості випадків комп’ютери
визначають рішення набагато швидше»
14

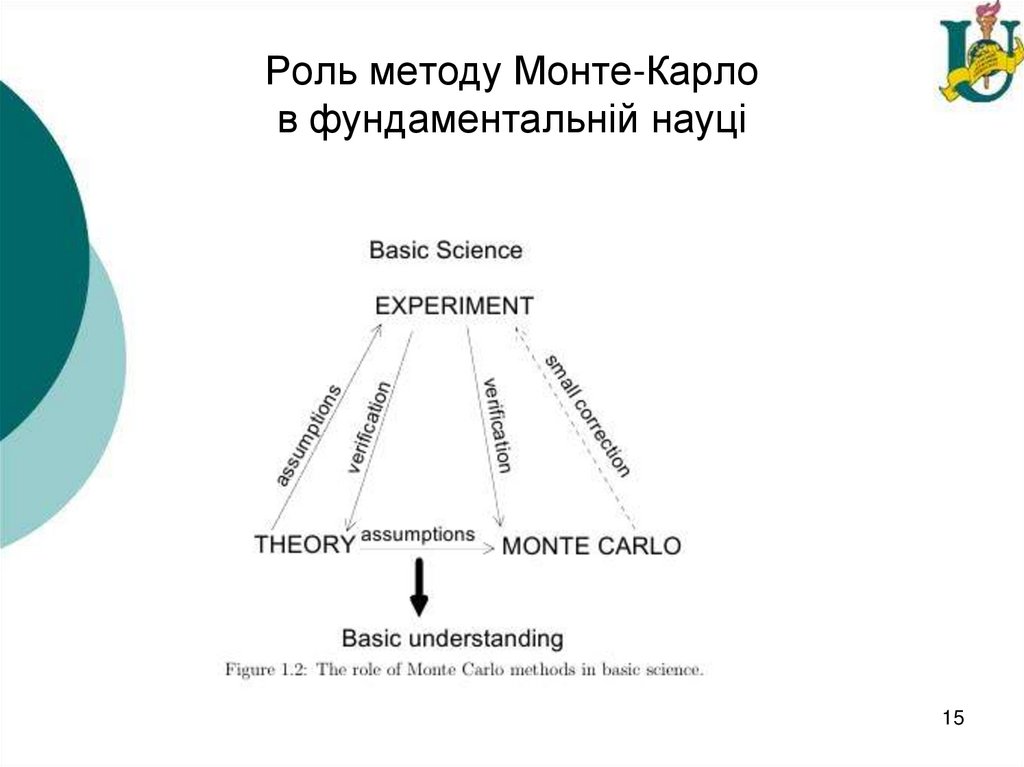
15. Роль методу Монте-Карло в фундаментальній науці

15

16. Роль методу Монте-Карло в фундаментальній науці

• Важлива роль, яку методи Монте-Карло мають
відігравати в цьому виді дослідження,
проілюстровано на рис. 1.2. Фундаментальна наука
намагається зрозуміти основні механізми роботи
явища. «Теорія» — це набір припущень (можливо, з
математичним формулюванням цих припущень), які
можна виміряти в «експерименті». В ідеалі зв'язок
між теорією і експериментом є прямим, щоб
інтерпретація експерименту була однозначною. Це
відбувається, коли математичний опис мікроскопічних
взаємодій і макроскопічних вимірювань не
передбачає подальшої апроксимації.
16

17.

• Алгоритми Монте-Карло, як правило, прості, гнучкі
та масштабовані. Застосовуючись до фізичних систем,
методи Монте-Карло можуть звести складні моделі до
набору основних подій та взаємодій, відкриваючи
можливість кодування поведінки моделі за допомогою
набору правил, які можуть ефективно
впроваджуватися на комп’ютері. Це, у свою чергу,
дозволяє впроваджувати та вивчати на комп’ютері
набагато загальніші моделі, ніж це можливо за
допомогою аналітичних методів.
17

18. Застосування

• Існує багато прикладів використання
методу Монте-Карло, які можна взяти з
соціальних наук, транспортного потоку,
зростання населення, фінансів,
генетики, квантової хімії, радіаційних
наук, радіотерапії та радіаційної
дозиметрії, але…
18

19.

Методи Монте-Карло (MC) — це підмножина
обчислювальних алгоритмів, які використовують процес
повторної випадкової вибірки для чисельних оцінок
невідомих параметрів. Вони дозволяють моделювати
складні ситуації, де задіяно багато випадкових змінних, і
оцінювати вплив ризику. Застосування MC неймовірно
широке та призвело до ряду новаторських відкриттів у
галузях фізики, теорії ігор та фінансів. Існує широкий спектр
методів Монте-Карло, але всі вони поділяють те спільне, що
вони покладаються на генерацію випадкових чисел для
вирішення детермінованих проблем. Я сподіваюся
окреслити деякі з основних принципів MC і, можливо,
заразити вас трохи захоплення, яке я маю щодо їх
можливого застосування.
19

20.

20

21. закон великих чисел говорить:

• «Зі збільшенням кількості ідентично
розподілених, випадково згенерованих
змінних, їх вибіркове середнє (середнє)
наближається до їх теоретичного
середнього».
Крім того, що він є одним із найважливіших
законів статистики, він є основою для
моделювання Монте-Карло та дозволяє нам
побудувати стохастичну модель методом
21
статистичних випробувань.

22.

• Якщо обіцянок багатства та знань було
недостатньо, щоб викликати ваш інтерес,
методи Монте-Карло ланцюга Маркова
пропонують потужний інструмент для
навчання алгоритмів глибокого навчання.
Науковці даних та інженери машинного
навчання можуть використовувати ці
методи, щоб робити різноманітні дивні та
чудові речі. Якщо вам цікаво прочитати
більше про Монте-Карло, я рекомендую
такі ресурси:
22

23.

• beginner: http://www.statisticshowto.com/
monte-carlo-simulation/
• intermediate: http://mathforum.org/library/d
rmath/view/51909.html
• advanced: http://farside.ph.utexas.edu/tea
ching/329/lectures/node109.html
• https://www.youtube.com/watch?v=OgO1g
pXSUzU
23

24.

+
•не потребує жодних припущень щодо
•забезпечує здійснення процедури навіть
у багатовимірному випадку.
•легко застосовується за малих обмежень
або без попереднього аналізу завдання.
•межі похибки точно не визначені, а
включають деяку випадковість;
•статистична похибка спадає дуже
повільно;
24

25. Як це працює??

На відміну від звичайної моделі прогнозування, моделювання
Монте-Карло передбачає набір результатів на основі
оціненого діапазону значень у порівнянні з набором
фіксованих вхідних значень. Іншими словами, симуляція
Монте-Карло будує модель можливих результатів за
допомогою розподілу ймовірностей, такого як рівномірний або
нормальний розподіл, для будь-якої змінної, яка має
притаманну невизначеність. Потім він знову і знову
перераховує результати, щоразу використовуючи інший набір
випадкових чисел між мінімальним і максимальним
значеннями. У типовому експерименті Монте-Карло цю
вправу можна повторювати тисячі разів, щоб отримати велику
кількість ймовірних результатів.
25

26. Як використовувати методи Монте-Карло

метод Монте-Карло передбачає три основні кроки:
1. Налаштуйте прогностичну модель, визначивши як залежну
змінну, яку потрібно спрогнозувати, так і незалежні змінні
(також відомі як вхідні, ризикові або предикторні змінні), які
керуватимуть прогнозом.
2. Вкажіть розподіли ймовірностей незалежних змінних.
Використовуйте історичні дані та/або суб’єктивне судження
аналітика, щоб визначити діапазон ймовірних значень і
призначити вагу ймовірності для кожного.
3. Повторно запускайте моделювання, генеруючи випадкові
значення незалежних змінних. Робіть це, доки не буде
зібрано достатньо результатів, щоб скласти
репрезентативну вибірку з майже нескінченної кількості
26
можливих комбінацій.

27. https://www.youtube.com/watch?v=7ESK5SaP-bc

https://www.youtube.com/watch
?v=7ESK5SaP-bc
•ДЯКУЮ
за увагу !
27

28.

28