Похожие презентации:
Економіко-математичні методи і моделі
1. Економіко-математичні методи і моделі
• Термін економіко-математичніметоди розуміється в свою чергу як
узагальнююча назва комплексу
економічних і математичних наукових
дисциплін, об'єднаних для вивчення
соціально-економічних систем і
процесів.
2. Розподіл годин
Лекції -18 годинПрактичні і лабораторні заняття -16 годин
Самостійна робота - 38 годин
Залік
-2
2
3.
Лекція 1Основні поняття
економетрії. Моделі парної
регресії.
Вступ
1.Об'єкт, предмет, мета i завдання
економетрії.
2. Кореляцiйно-регресiйний аналіз в
економіці.
3. Моделі парної регресії та їх дослідження.
4. Метод найменших квадратів.
4. Вступ
Економетрія(економетрика)
Дуже
широко
буквально означає
"вимірювання в
економіці"
4
5.
Економетріяце
наукова
дисципліна, яка вивчає комплекс
економіко-математичних
методів і побудованих на їх основі
моделей
для
кількісного
вимірювання взаємозв`язків між
економічними показниками.
5
6. 1.Об'єкт, предмет, мета i завдання економетрії
Об'єктЕкономічні системи
та простори
різного рівня
складності
Підприємства
Фірми
Окремі галузі
Регіони
Держави
6
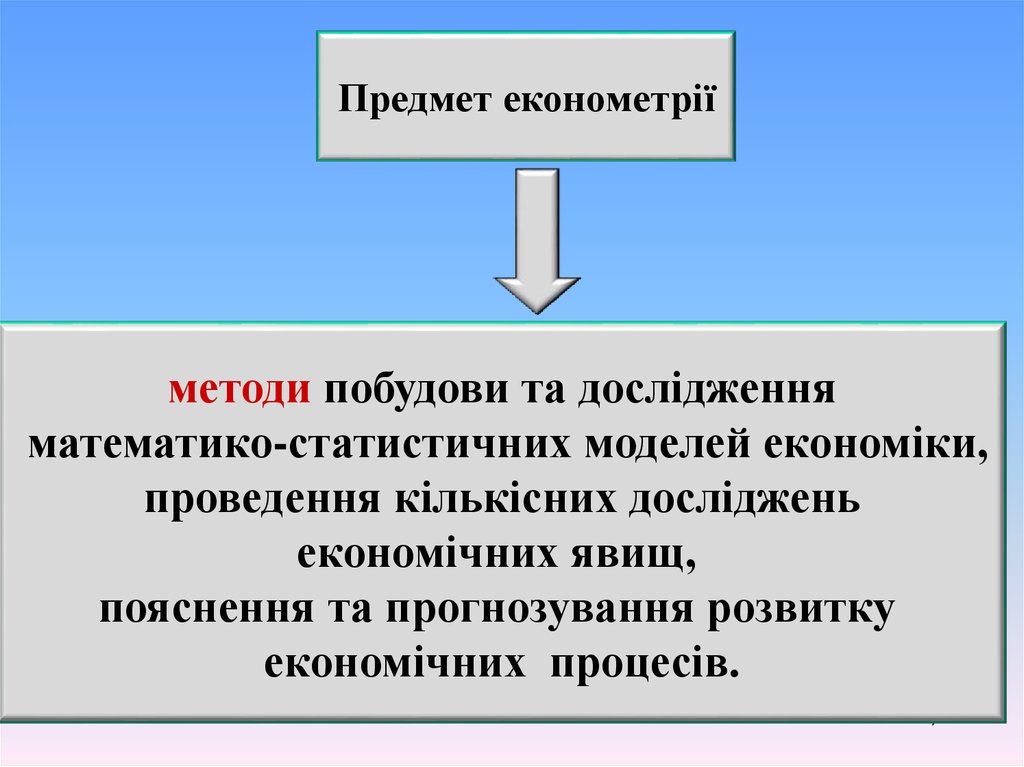
7.
Предмет економетріїметоди побудови та дослідження
математико-статистичних моделей економіки,
проведення кількісних досліджень
економічних явищ,
пояснення та прогнозування розвитку
економічних процесів.
7
8.
Метою економетричного дослідження єаналіз реальних економічних систем i
процесів, що в них відбуваються, за
допомогою економетричних методів i
моделей, їх застосування при прийнятті
науково обґрунтованих управлінських
рішень.
8
9.
Основне завдання економетрії•оцінити параметри моделей з
урахуванням особливостей вхідної
економічної інформації,
•перевірити відповідність моделей
досліджуваному явищу
•спрогнозувати розвиток економічних
пpoцecів.
9
10. Основні етапи економетричного аналізу
1) вибiр конкретної форми аналітичної залежностіміж економічними показниками (специфікація моделі)
на підставі відповідної економічної теорії;
2) збирання та підготовка статистичної інформації;
3) оцінювання параметрів моделей;
4) перевірка адекватності моделі та достовірності її
параметрів;
5) застосування моделі для прогнозування розвитку
економічних процесів з метою подальшого керування
ними.
10
11. Коротка історична довідка
“Гарвардський барометр”, задопомогою якого
в 20-тi роки намагалися передбачити
поведінку
товарного і грошового ринку.
11
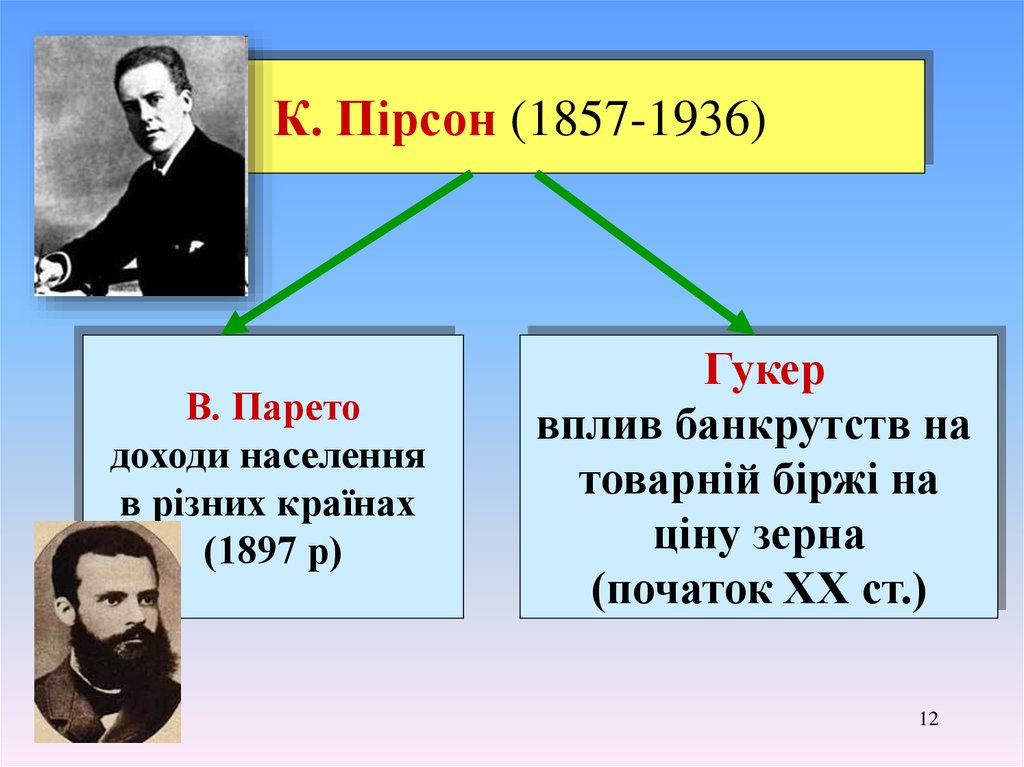
12.
К. Пiрсон (1857-1936)В. Парето
доходи населення
в різних країнах
(1897 р)
Гукер
вплив банкрутств на
товарній біржі на
ціну зерна
(початок ХХ ст.)
12
13.
Ч. Кобб i П. Дугласвиробнича функція
(1928 р.)
П. Дуглас
Економетрія як окрема галузь
(1930 р.)
"Міжнародне товариство
для розвитку економічної теорії
і її зв'язку зі статистикою та математикою".
13
14.
Термін "економетрія" вперше запровадивльвівський вчений
П.Чомпа, який опублікував у
Львові в 1910 р. книгу
"Нариси економетрії i природної
теорії бухгалтерії, яка ґрунтується
на політичний економії".
Р. Фрiш
Засновники економетрії
Р. Фрiш,
Е. Шумпетер,
Я. Тiнберген
Е.Шумпетер
14
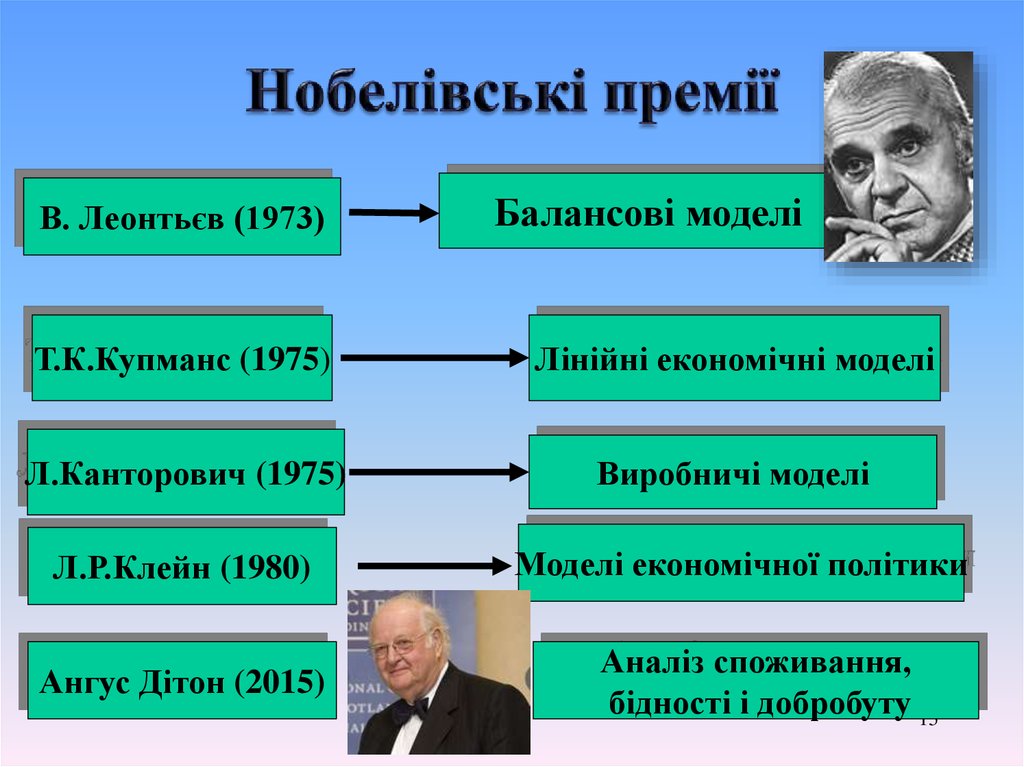
15.
В. Леонтьєв (1973)Балансові моделі
Т.К.Купманс (1975)
Лінійні економічні моделі
Л.Канторович (1975)
Виробничі моделі
Л.Р.Клейн (1980)
Моделі економічної політики
Ангус Дітон (2015)
Аналіз споживання,
бідності і добробуту 15
16. 2. Кореляцiйно-регресiйний аналіз в економіці
Статистичною називають залежність,коли зі змінюванням однієї випадкової величини
змінюється закон розподілу ймовірностей іншої.
Зокрема,
статистична
залежність
виявляється в тому, що зі змінюванням однієї
величини змінюється середнє значення іншої.
Така залежність називається кореляційною.
16
17.
РівноправніX
Y
17
18.
НерівноправніX
Y
Регресанд
(залежна)
Регресор
(незалежна)
Умовне
математичне
сподівання
M Y / x f ( x)
функція
регресії
У на Х.
18
19.
Парна регреcіяM Y / x f ( x)
Множинна регресія
M Y / x1 , x2 ,..., xm f ( x1 , x2 ,..., xm )
19
20.
Термін “регресія” від латинськогоregressio – рух назад, введено
англійським статистиком Френсісом
Гальтоном
20
21.
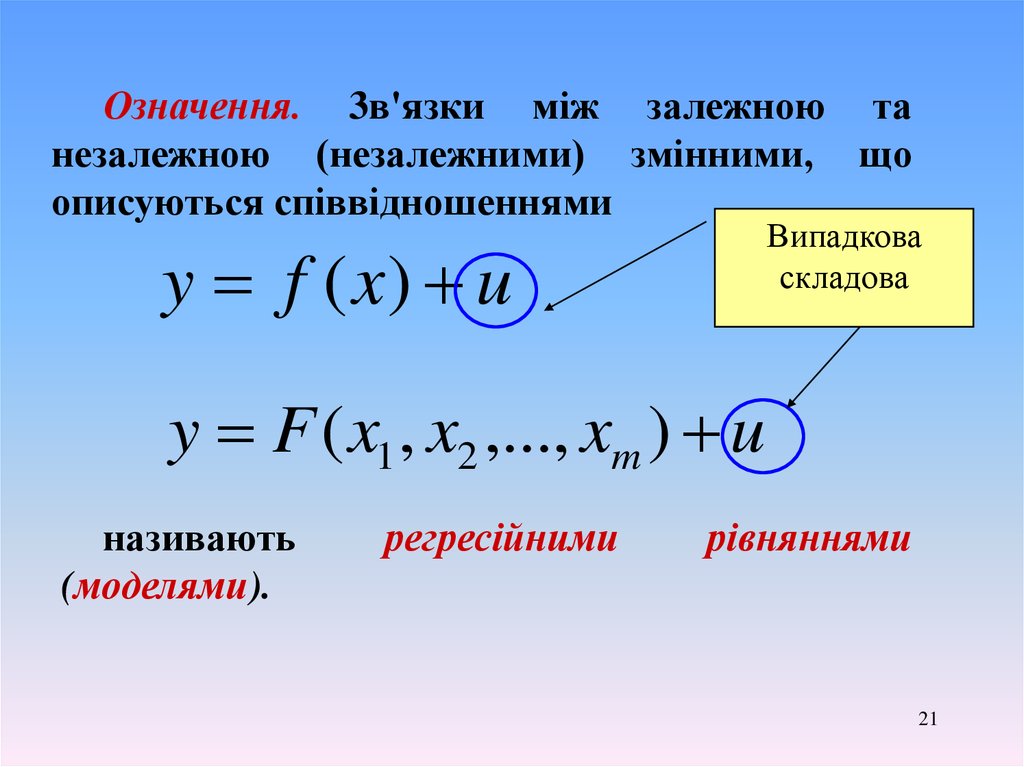
Означення. 3в'язки між залежною танезалежною (незалежними) змінними, що
описуються співвідношеннями
Випадкова
складова
y f ( x) u
y F ( x1 , x2 ,..., xm ) u
називають
(моделями).
регресійними
рівняннями
21
22.
Причини присутності в регресійнихмоделях випадкового фактора
(відхилення)
1. Уведення
в модель не всіх пояснюючих
змінних.
2. Неправильний вибір функціональної
форми моделі.
3. Агрегування змінних.
4. Помилки вимірювань.
5. Обмеженість статистичних даних.
6. Непередбачуваність людського фактору.
22
23.
Сукупність методів, задопомогою яких досліджуються
та узагальнюються
взаємозв'язки кореляційно
пов'язаних змінних, називається
кореляцiйно-регресiйним
аналізом.
23
24.
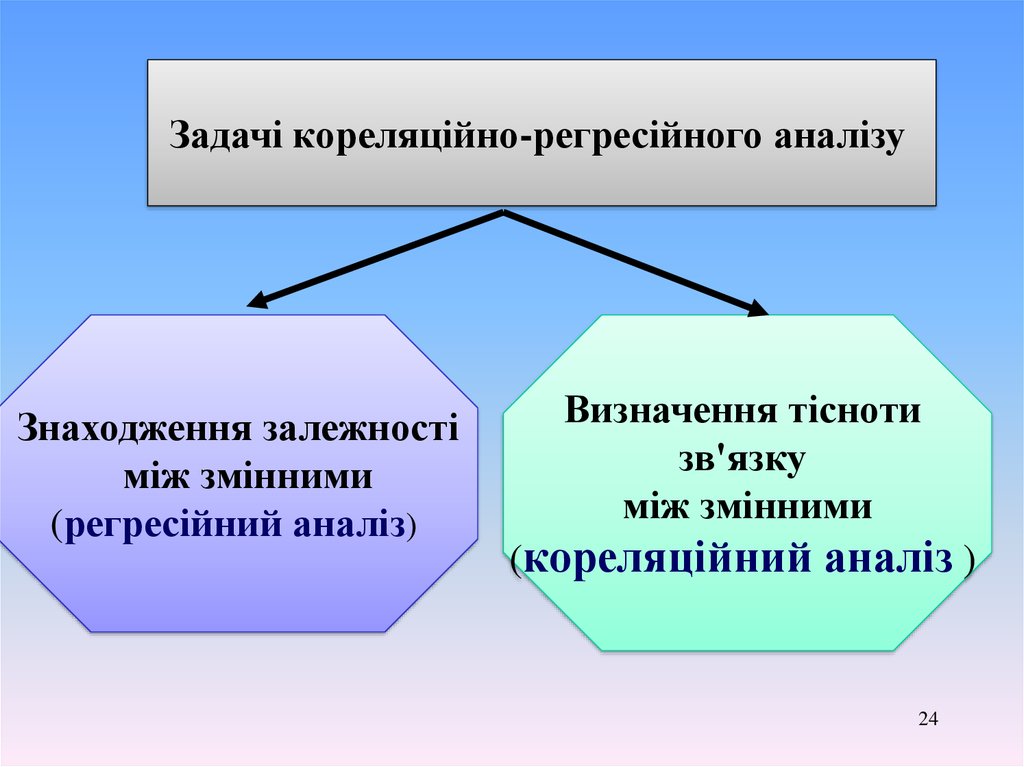
Задачі кореляцiйно-регресiйного аналізуЗнаходження залежності
між змінними
(регресійний аналіз)
Визначення тісноти
зв'язку
між змінними
(кореляцiйний аналiз )
24
25.
Етапи побудови рівняння регресії1. Вибір форми рівняння регресії
( сnецифiкацiя моделі )
2. Визначення параметрів обраного рівняння
3. Аналіз якості рівняння
та перевірка адекватності рівняння
емпіричним даним, удосконалення рівняння.
25
26.
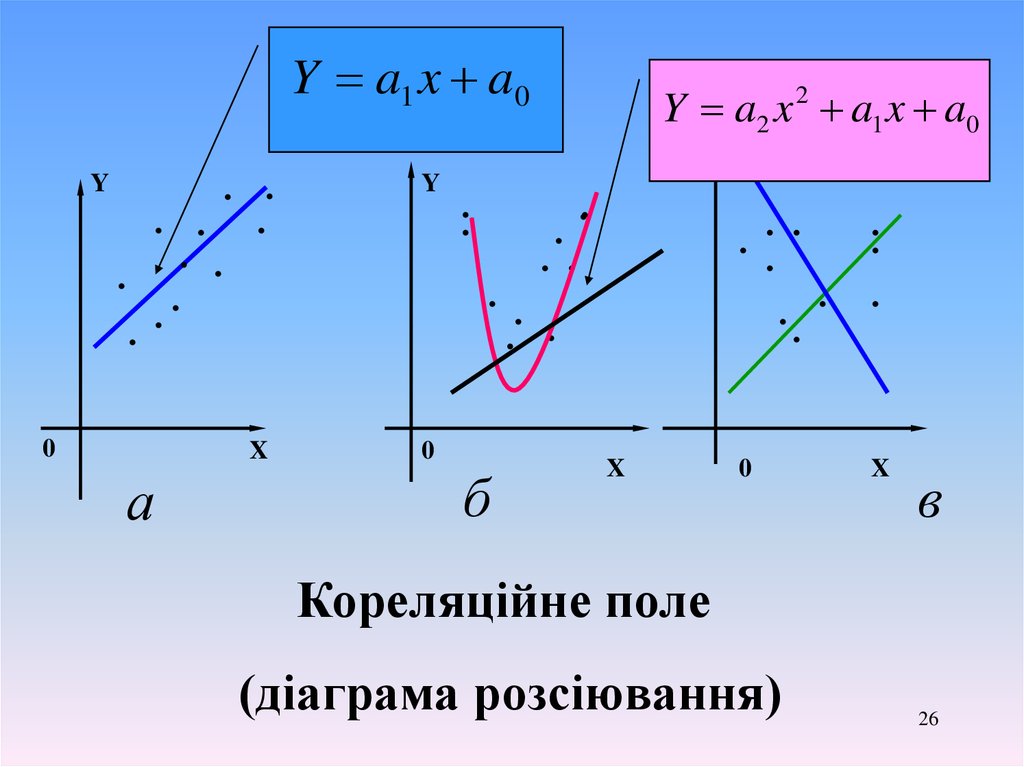
Y a1 x a0Y
. .
. .
.
. .
.
.
.
.
Y
X
0
0
а
Y a2 x 2 a1 x a0
Y
.
.
.
.
.
. .
.
б
. .
.
. .
.
.
X
0
.
.
.
.
.
X
в
Кореляційне поле
(діаграма розсіювання)
26
27. 3. Моделі парної регресії та їх дослідження.
Рівень доходуСпоживання
Ціна товару
Попит
Розмір основних
фондів
Обсяг
виробництва
27
28.
Модель КейнсаС
індивідуальне
споживання
Y
прибуток
C c0 bY
де со - величина автономного споживання;
b - гранична схильність до споживання (0<b 1).
28
29.
Залежність між рівнем безробіття х iрівнем інфляції у відображається так
званою кривою Фiлiпса:
a
y
x b
де а > 0, b > 0 - параметри моделі,
а змінні х i у вимірюються у процентах.
29
30.
При незмінний річний дисконтній(обліковій) ставці r i початковому внеску
а через х років у банку наявна сума
грошей обчислюватиметься за формулою
y a(1 r )
x
де а, r - параметри моделі.
30
31.
При маркетингових i ринковихдослідженнях, при дослідженні збуту
продукції та в демографії застосовують так
звану криву Гомперця:
y e
ab c
x
де параметри а та с можуть набувати
будь-яких значень,
а b перебуває в межах: 0 < b < 1.
31
32.
У загальному випадку nарна лінійна регресія єлінійною функцією мiж залежною змінною У i
однiєю пояснюючою змінною Х:
Y a1 X a0
Це спiввiдношення називається теоретичною
лінійною регресiйною моделлю
а0 i а1 - теоретичні параметри
(теоретичні коефіцієнти) peгpeciї.
32
33.
За вибiркою обмеженого обсягу будуютьтак зване емпіричне рівняння peгpecii, у
якому
коефіцієнтами
є
оцінки
теоретичних коефiцiєнтiв регресії:
~ ~
~
Y a1 X a0
~
~
a1 i a0
де
— оцінки невідомих
параметрів а1 i а0 .
33
34.
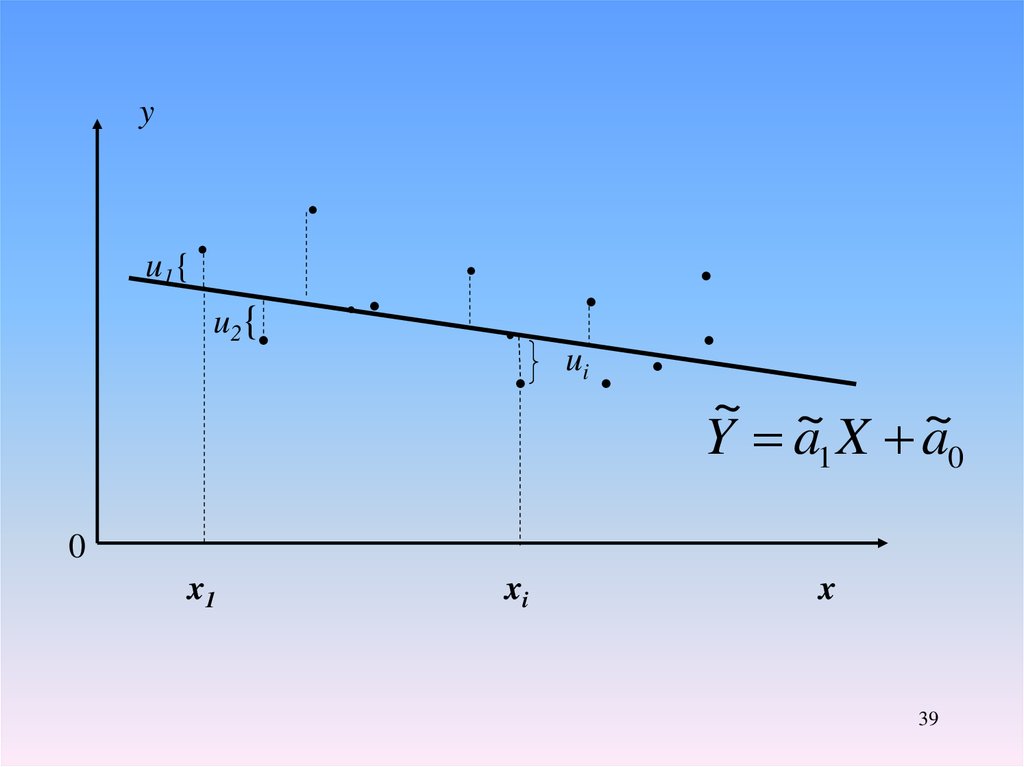
yu1{
.
.
1
.
M(Y/X)=a0+a1X
..
.
i
.
.
.
.
. ui . .
~ ~
~
Y a1 X a0
0
x1
xi
x
34
35.
Задачі лінійного регресiйного аналізу полягаютьу тому, щоб за наявними статистичними даними
( xi , yi ), i 1, n
для змінних Х i У:
~
~
а) отримати найкращі оцінки a1 i a0невідомих
параметрів а1 i а0 ;
б) перевірити статистичні гіпотези про
параметри моделі;
в) перевірити, чи досить добре модель
узгоджується зi статистичними даними
(адекватність моделі даним спостережень).
35
36.
Для відображення того факту, що кожнеіндивідуальне значення yi відхиляється від
відповідного умовного математичного
сподівання, у модель уводять випадковий
доданок ui:
~
~
yi M Y / x xi ui a0 a1 xi ui
Таким чином, регресiйне рівняння набуває вигляду
~
~
Y a0 a1 X u
36
37.
Мiрою якостi знайдених оцiнок можуть бути визначенікомпозиції вiдхилень
n
n
n
i 1
i 1
i 1
ui , i 1, n
~
~ a~ x )
u
(
y
y
)
(
y
a
i i i i 0 1i
n
n
n
~
~ a~ x
u
y
y
y
a
i i i i 0 1i
i 1
n
i 1
i 1
n
n
i 1
i 1
метод
найменших
модулів (МНМ).
метод
найменших
квадратів
(МНК).
2
1 i
2
~
~
~
ui ( yi yi ) ( yi a0 a x )
i 1
2
37
38. 4. Метод найменших квадратів
x1x2
x3
. . . xn-1
xn
y1
y2
y3
. . . yn-1
yn
38
39.
yu1{
.
.
u2{.
..
.
.
.
.
.
. ui . .
~ ~
Y a1 X a~0
0
x1
xi
x
39
40.
nn
n
i 1
i 1
2
~ , a~ ) ( y ~
~ a~ x ) 2 min
u
Q
(
a
y
)
(
y
a
i
i i i 0 1i
0
1
2
i 1
Необхідною умовою існування мінімуму неперервної
диференційованої функції двох змінних є рівність нулю її частинних
похідних.
Так як
~
Y
x;
a1
~
Y
1;
a0
~
Y
xi ;
a
1 i
~
Y
1;
a
0 i
40
41.
nQ
aˆ 2 y i aˆ 1 x i aˆ 0 x i 0
1
i 1
n
Q
2 y i aˆ 1 x i aˆ 0 0
aˆ 0
i 1
n
n
n 2
aˆ 1 xi aˆ0 xi xi yi ;
i 1
i 1
i 1
n
n
aˆ
ˆ
1 x i a0 n y i
i 1
i 1
41
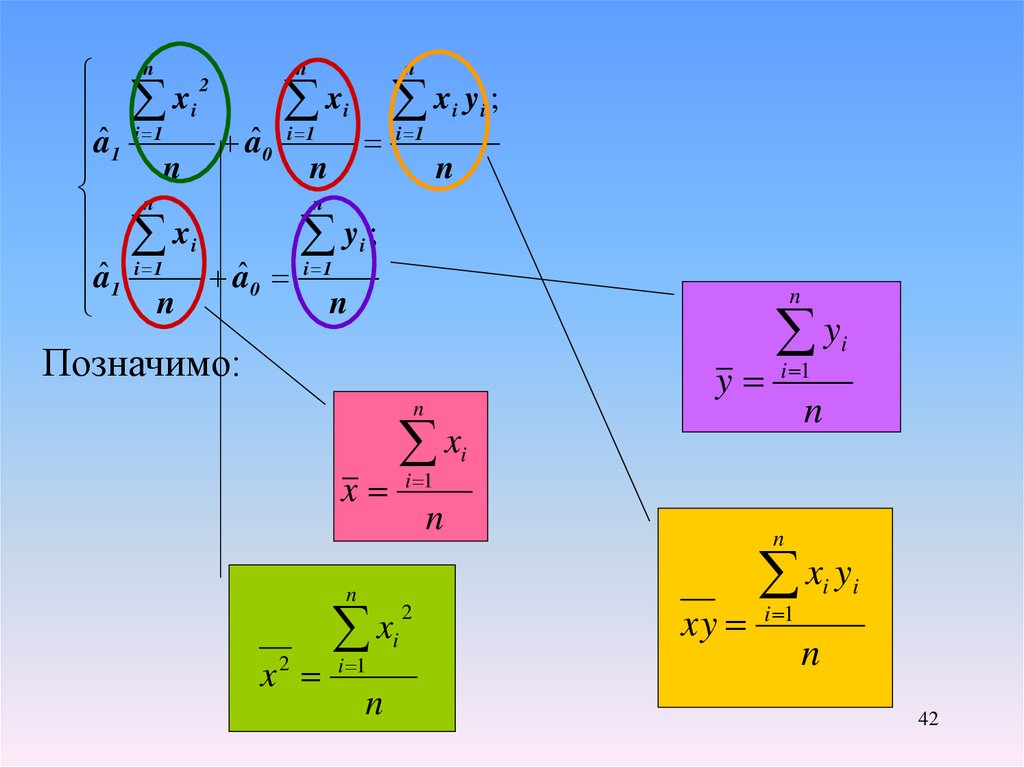
42.
aˆ 1aˆ 1
n
x
i 1
n
2
i
n
aˆ0
x
i 1
i 1
n
i
n
n
x
n
x y ;
i
i 1
i
n
n
i
aˆ0
y;
i
i 1
n
n
Позначимо:
y
n
x
n
x
2
xi
i 1
n
y
i 1
n
x
i 1
i
n
2
i
n
xy
x y
i
i 1
i
n
42
43.
одержимоaˆ1 x 2 aˆ0 x xy
aˆ1 x aˆ0 y
n
звідки маємо
xy x y
aˆ1 2
2
x x
aˆ y aˆ x
1
0
x
x
i
i 1
n
n
x2
x
i 1
n
n
i
y
y
i
i 1
n
n
2
xy
x y
i
i 1
n
43
i
44.
Коефіцієнт кореляціїrxy
S xy
Sx S y
xy x y
x x y y
2
2
2
2
0 rxy 1
44
45. Завдання
За 10 парами спостережень отримано такі результати:10
y
10
xi 100
i 1
i 1
10
10
x y
i 1
i
i
200
xi 12000
21000
10
i
2
i 1
yi 45000
2
i 1
За МНК оцініть коефіцієнти рівняння регресії Y на X .
Оцініть коефіцієнт кореляції rxy
45































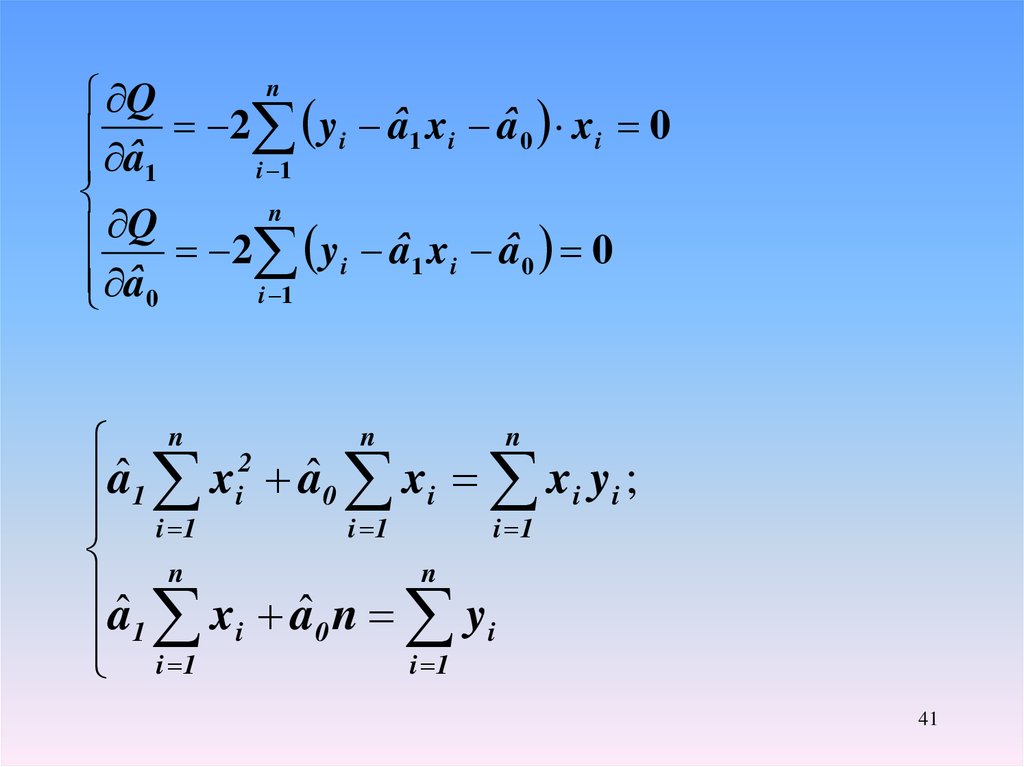



 Математика
Математика Экономика
Экономика








