Векторная алгебра. Аналитическая геометрия. Линии второго порядка

1.

ВЕКТОРНАЯ АЛГЕБРА.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
ЛИНИИ
ВТОРОГО ПОРЯДКА

2.

Кривой второго порядка называется линия,
заданная уравнением второй степени
относительно координат x и y:
M (x; y)
у Окружность
Окружностью радиуса R с центром точке М0
R М плоскости таких,
называется множество точек
что
M0 (x0; y0)
O
Найдём уравнение окружности.
x

3.

Дано: М0(x0;y0) – центр окружности,
R – расстояние от центра окружности до любой
её точки M(x;y)
Найти: F(x; y) = 0 – уравнение окружности
Решение
Тогда
По условию
или
_
каноническое уравнение окружности.
Если х0=0, у0=0, то получим уравнение
окружности с центром в начале координат:

4.

Пример. Составить уравнения окружности, если:
а) центром окружности является начало координат,
а её радиус равен 4;
б) центром окружности является точка М0(3;-2),
а её радиус равен 5;
в) окружность проходит через точку М(3;7), а её
центр лежит в точке М0(0;3);
г) точки М1(4;3) и М2(0;7) являются концами
одного диаметра.

5.

Эллипс множество точек
Эллипсом называется
Правописание…
плоскости, для каждой из которых сумма
Пожалуйста, не повторяйте ошибок некоторых пользователей
расстояний до двух данных точек F1 и F2
поисковых интерент-систем, которых интересует «как построить
плоскости
(фокусов),
есть постоянная
величина
эллибз», «отличие
элипса от овала»
и «эксцентриситет
элебса». 2a,
причем она больше, чем расстояние 2c между
фокусами:
y
O
x

6.

Найдём зависимость между координатами x и y
Запишем расстояние между
F1 и M в координатах
y
точек M таких, что
Раскроем скобки и
вынесем, где
возможно, за
скобки (a2-c2)
Запишем расстояние между F2 и M
в координатах
O
x

7.

>0, так как 2a>2c, a>c
Сравните
с нулём
2 2
2
эту разностьa -c можно обозначить как b :
>0
―
каноническое уравнение эллипса

8.

Исследуем форму эллипса по его каноническому
уравнению:
1. Уравнение эллипса содержит х и у
в чётной степени.
Как этот
факт связывает
точки M(x;y),
M1(x;-y),
Для эллипса
осями
симметрии
являются
M2(-x;y), M3(-x;-y)?
оси координат, а центром
симметрии –
начало координат.
2. Из уравнения эллипса следует, что каждое
слагаемое не больше единицы:
Эллипс расположен внутри
прямоугольника,
образованного прямыми x=a, x=-a, y=b, y=-b.
Докажите утверждение, решив неравенства

9.

3. Из уравнения эллипса найдём координаты
точек пересечения эллипса с осями координат:
Найдём значения x из уравнения эллипса при y=0, ―
Найдём значения у из уравнения эллипса при х=0.
вершины эллипса;
При a>b отрезок ОА (или ОАʹ) называется
большой полуосью, отрезок ОВ (или ОВʹ) –
малой
полуосью,
отрезок
ААʹ – большой осью,
При увеличении
значения
x
отрезокот 0ВВʹ
– малой
осью.
до а значение
у
уменьшается,
Фокусы
эллипсазначит
расположены на большой оси.
функция вэллипс
I четверти
4. Исследуем
на…возрастание или убывание
в I четверти, выразив у из уравнения эллипса.
5. Используя симметрию эллипса, строим его.

10.

3. Из уравнения эллипса найдём координаты
точек пересечения эллипса с осями координат:
―
Найдём значения x из уравнения эллипса при y=0,
вершины
эллипса;
Найдём значения у из уравнения эллипса при х=0.
При a>b отрезок ОА (или ОАʹ) называется
большой полуосью, отрезок ОВ (или ОВʹ) –
малой
полуосью,
отрезок
ААʹ – большой осью,
При увеличении
значения
x
отрезокот 0ВВʹ
– малой
осью.
до а значение
у
уменьшается,
Фокусы
эллипсазначит
расположены на большой оси.
функция вэллипс
I четверти
4. Исследуем
на…возрастание или убывание
в I четверти, выразив у из уравнения эллипса.
5. Используя симметрию эллипса, строим его.

11.

Сравните три величины:
ε, 0, 1
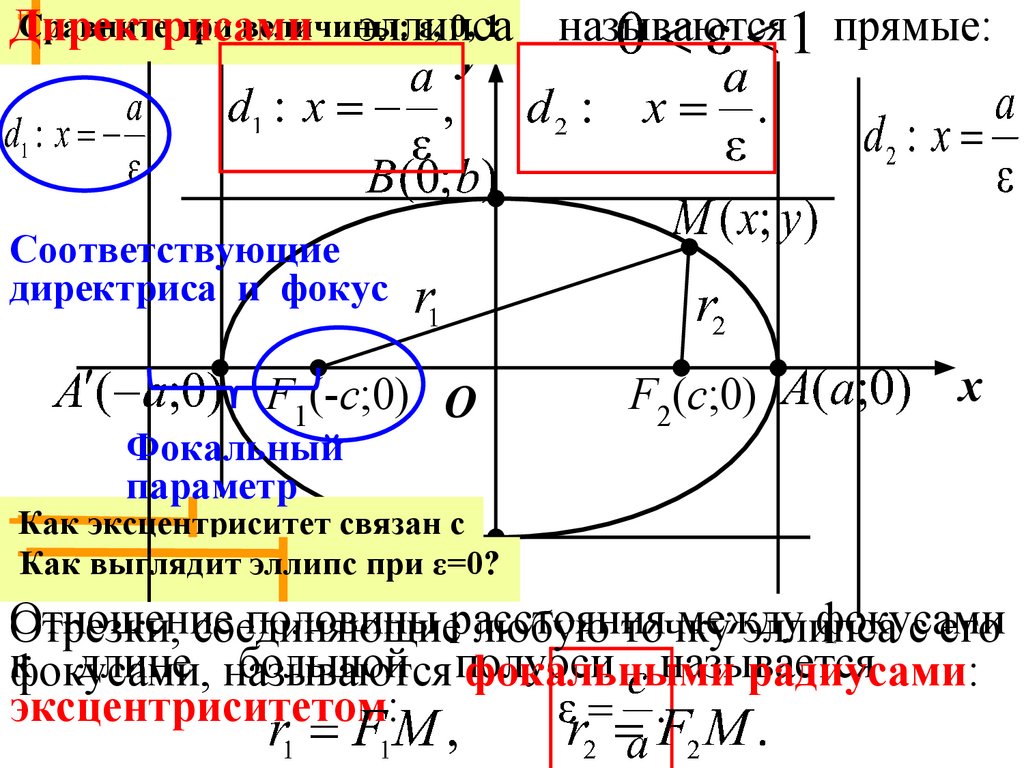
Директрисами
эллипса
называются прямые:
у
Соответствующие
директриса и фокус
F1(-c;0) O
F2(c;0)
x
Фокальный
параметр
Как эксцентриситет связан с
Как выглядит
эллипс при ε=0?
формой эллипса?
Отношение
половины расстояния
между
фокусами
Отрезки, соединяющие
любую точку
эллипса
с его
кфокусами,
длине называются
большой полуоси
называется
фокальными
радиусами:
эксцентриситетом:

12.

Пример. Найти полуоси, фокусы и
эксцентриситет эллипса
и схематично его построить.